基于VIKOR妥协解的供应商评价方法优化
王庆军,方良元
(合肥工业大学 管理学院,合肥 230009)
供应链管理强调供应商与核心企业之间的战略合作伙伴关系,并以此形成单个企业所不能产生的共赢优势[1]。逼近理想解的排序法(Technique for Order Preference by Similarity to Ideal Solution,TOPSIS)是多指标决策问题常用的一种方法[2],灰色关联分析法(Grey Relational Analysis,GRA)是对系统动态过程的发展态势进行量化比较的分析方法[3],TOPSIS法反映的是备选供应商与理想供应商之间的整体接近程度,而GRA 法反映的是各备选供应商与理想供应商在内部因素上的变化趋势,这两种方法优势互补。因此,结合TOPSIS 法和GRA 法两种方法,其结果可同时反映备选供应商与正负理想供应商之间的整体接近程度及发展态势的相似程度,评价结果更为科学全面,同时可以解决TOPSIS法和GRA 法评价结果不一致的矛盾。
易海峰(2010)在其文章中将TOPSIS法距离值和GRA 法灰色关联值采用简单的线性加权方法进行了合并,但在合并计算时,采用主观赋值法确定合并权重,致其评价结果带有较大的主观性,科学性有待进一步提高。
VIKOR 法是Opricovic于1998年提出,是多属性决策中最佳化妥协解方法之一[4]。它是基于理想点法来排列各供应商的优先顺序[5]。其最大特色就是将群体效益最大化以及将反对意见的个别遗憾最小化,所以其妥协解可被决策者接受。
本文拟在运用TOPSIS法和GRA 法的基础上,采用折衷妥协的思想,探讨构建基于VIKOR 妥协解的综合模型,综合考虑距离值和关联度,运用VIKOR 法求解距离值与关联度的妥协解;并以此妥协解对供应商进行综合评价,最终选择出最佳供应商。
一、VIKOR 综合模型构建
1.数据标准化处理
设备选供应商有m 个,评价指标有n个,每个指标值为aij(1≤i≤m,1≤j≤n),构造指标决策矩阵A=(aij)m×n,由于各指标的量纲不同,采用下式对决策矩阵进行标准化处理:

由此得到标准化矩阵X=(xij)m×n。
2.评价指标权重确定
评价指标权重的确定是求解多指标决策问题的关键。确定指标权重的方法有主观法和客观法两大类。但主观法所确定的指标权重受决策者意向的影响较大,会导致评价结果具有较大的主观随意性,为此文章采用熵权法确定评价指标权重避免主观干扰。
对标准化矩阵按公式(2)进行归一化处理,并按公式(3)求得各指标的熵值ej。

根据公式(4)计算得到第j个指标的差异系数gj为:

当gj值越大时,说明指标间差异程度越高,对应的指标越为重要,由此得到熵权wj:

3.TOPSIS距离值计算
计算得到加权标准化矩阵:

根据矩阵,确定正理想解和负理想解为:

其中,Jl为效益型因素指标集合,J2为成本型因素指标集合。
根据距离公式,计算出各备选供应商与正理想解和负理想解之间的距离如下:

4.GRA 关联度计算
计算各备选供应商与正理想解V+和负理想解V-的灰色关联系数矩阵C+和C-,其中:

其中,ρ称为分辨系数[6],ρ越小,分辨力越大,一般ρ的取值区间为(0,1),当ρ≤0.5463时,分辨力最好,文章取ρ=0.5。
由此计算各备选供应商与正理想解和负理想解的灰色关联度ri+和ri-:

5.VIKOR 妥协解计算
为了综合考虑各备选供应商与正理想解和负理想解之间的距离值以及各备选供应商与正理想解和负理想解的灰色关联度,构造出包含这四个指标的决策矩阵Y:

根据2.1节,对其进行无量纲化处理得到标准化矩阵Z=(Zik)m×4;
根据2.2节,采用熵权法计算出各指标的熵权wk;
根据2.3节,计算加权标准化矩阵F=(fik)m×4,并得到各指标的正负理想解f+和f-;
计算各备选供应商的Si和Ri值:

其中,Si代表备选备选供应商的群体效益,Si值越小,群体效用越大;Ri代表个别遗憾,Ri值越小,个别遗憾越小。
计算各备选供应商的妥协解Qi:
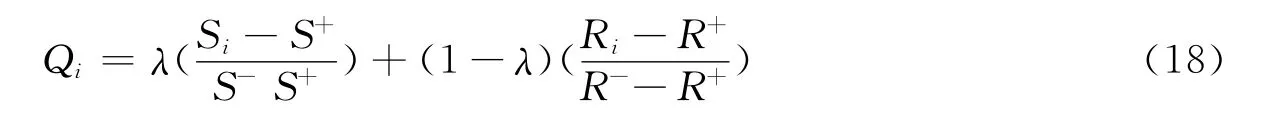
其中,S+=miniSj;S-=maxiSj;R+=miniRj;R-=maxiRj
λ为最大化群体效用决策机制系数[7],λ>0.5时表明决策者决策时侧重把最大化群体效用的情况作为决策依据;λ<0.5时表示决策者决策时侧重把最小化个别遗憾的情况作为决策依据;文章在此取λ=0.5,表示折衷情况,以最大化群体效益同时最小化个别遗憾。Qi越小,意味着备选供应商越好。
6.评价选择
根据Qi、Si和Ri值升序分别对备选供应商进行优劣排序。
当以下两个条件满足时,最佳供应商就是根据Qi排序首位的供应商[8]。
条件1:可接受的优势条件:

其中,根据Q 值升序排列在首位的供应商记为F1,根据Q 值升序排列在次位的供应商记为F2,接受评价的备选供应商数目记为I。
如果排序的供应商为多个时,则需依序比较排序首位与排序之后各供应商之间是否满足条件1。
条件2:可接受的决策可靠度
根据Q 值排序首位的供应商的S值必须同时比排序次位的供应商的S值表现好。或者依据Q 值排序首位的供应商的R 值必须同时比排序次位的R 值表现好。
如果排序供应商为多个时,则需依次比较排序首位与排序之后各供应商之间是否满足条件2。
评判准则[9]:
如果排序首位和排序次位的两备选供应商彼此之间的关系同时满足条件1 和条件2 时,则接受排序首位的供应商为最优供应商;如果排序首位和排序次位的两供应商彼此之间的关系只符合条件2时,则同时接受排序首位和次位的供应商为最优供应商;如果排序首位的供应商同时和其他数个供应商之间均不符合条件1,而只符合条件2 时,则同时接受这些不符合条件1的供应商为最优供应商。
二、供应商评价选择算例
某建筑公司施工所需的某一物资共有六个供应商,分别为S1,S2,S3,S4,S5和S6。现需对六个供应商进行评价选择,以选择出最佳供应商建立战略合作伙伴关系。对供应商企业进行准确评价是一个系统工程,需要构建一个评价指标体系[10]。鉴于文章的研究重点不是评价指标体系的建立,故采用该公司现行的评价指标,主要有:信誉评价(10分)、资金能力(20分)、履约评价(包括供应能力、产品质量、售后服务三个二级指标,共60分)和合作态度(10分)共4大类指标。由该公司负责供应商工作的几位主要主管对各供应商的每个指标进行打分,然后再取平均值,得到最终的评价值如表1所示:

表1 供应商指标评价值表
1.TOPSIS法评价
根据前述章节,计算出各供应商的TOPSIS距离值如表2所示:

表2 供应商TOPSIS距离值表
由下列公式计算各供应商的TOPSIS评价值,即与理想解的相对接近度:

得到各供应商的TOPSIS评价值及排序如表3所示:

表3 供应商TOPSIS评价值排序表
选择TOPSIS评价值最大的供应商S3为最优供应商。
2.GRA 法评价
根据前述章节,计算出各供应商的灰色关联度如表4所示:
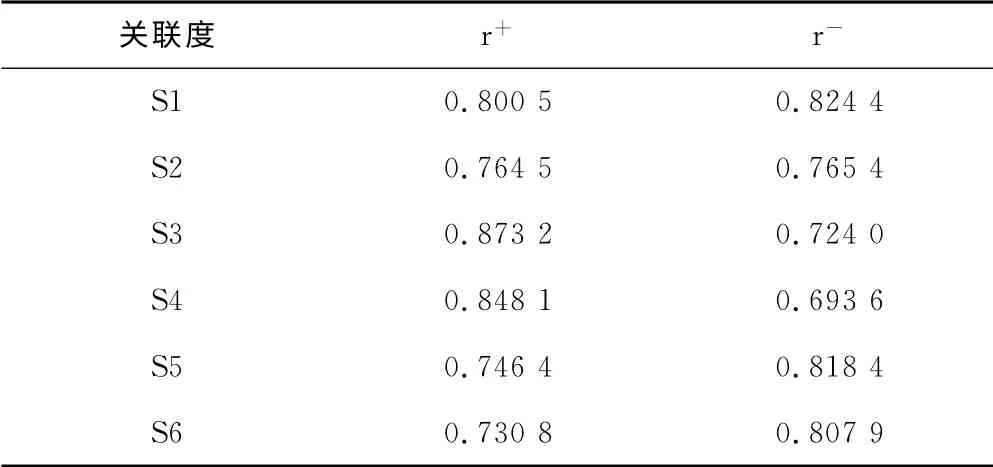
表4 供应商GRA 关联度表
根据下列公式计算各供应商的GRA 评价值,即灰色关联相对贴近度:

得到各供应商的GRA 评价值及排序如表5所示:

表5 供应商GRA 评价值排序表
选择GRA 评价值最大的供应商S4为最优供应商。
3.VIKOR 综合评价
由前述章节的结果可以看出,使用TOPSIS法选择出的最优供应商为S3,而使用GRA 法选择出的最优供应商为S4,评价结果不一致。为此,下文将使用VIKOR 法构建综合模型,求解距离值和关联度的妥协解,综合评价各供应商。

表6 供应商Si、Ri 及Qi 值表
根据Qi、Si和Ri值升序分别对供应商进行优劣排序如表7所示:

表7 供应商排序表
由上表可以看出,根据Q 值排序后,排序第一的供应商的S 值也同时比排序第二的S 值表现好,并且依据Q 值排序后,排序第一供应商的R 值也同时比排序第二的R 值表现好,即满足条件2。
经计算:

即满足条件1,接受排序第一的供应商S3为最优供应商。
4.评价结果的分析
由前述章节可以看出:
(1)采用TOPSIS法,即关注整体接近程度时,最优供应商为S3;
(2)采用GRA 法,即关注内部因素的变化趋势时,最优供应商为S4;
(3)采用VIKOR 综合法,即同时关注整体接近程度以及内部因素的变化趋势时,最优供应商为S3。
构造的四个综合决策指标中,通过熵权法确定的d+及d-的权重较大,这两个综合指标很大程度上决定了VIKOR 综合模型最后的评价结果,由此导致采用VIKOR 综合模型和采用TOPSIS法的评价结果一致。但VIKOR 综合模型是对TOPSIS法和GRA 法的综合及折衷,是同时考虑了各备选供应商与理想供应商之间的整体接近程度以及他们的在内部因素上的变化趋势,在理论层面提高了评价方法的科学全面性,因此其评价结果具备较强的可信度。
故此,接受备选供应商S3为该建筑公司的最佳供应商。
三、研究总结
在理论层面上,文章探讨构建了基于VIKOR 妥协解的综合模型,将TOPSIS法和GRA 法进行了综合,改进供应商评价方法。同时在实践层面上,文章通过VIKOR 综合模型的运用,为案例公司评价选择出最佳供应商,并以此验证了该综合模型的可行性。
本研究仅是基于综合与折衷理念构建评价模型的初步探索,当供应商评价指标的种类和数量发生改变时,VIKOR 综合模型的适用性和优越性,尚有待于从理论和实践层面进一步证明。
[1]周文坤,蒋文春.基于改进TOPSIS法的供应商选择方法[J].运筹与管理,2005,14(6):39-44.
[2]Hwang C L,Yoon K P.Multiple Attribute Decision Making Methods and Applications[M].New York:CRC Press,2011:69-71.
[3]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[4]刘鸿雁,孔 峰.VIKOR 算法在房地产估价中应用研究[J].西安建筑科技大学学报(自然科学版),2012,44(5):731-735.
[5]Opricovic S,Tzeng G H.Compromise solution by MCDM methods:A comparative analysis of VIKOR and TOPSIS[J].European Journal of Operational Research,2004,156(2):445-455.
[6]王 飞,杜晓丽.基于熵权-灰色关联-TOPSIS的低碳经济综合评价[J].科技管理研究,2013,(7):48-51.
[7]孔 峰,贾 宇,贾 杰.基于VIKOR 法的企业技术创新综合能力评价模型研究[J].技术经济,2008,27(2):26-30.
[8]刘永廷,崔新春.一种基于VIKOR 的设备优选方法[J].曲阜师范大学学报(自然科学版),2013,39(3):51-56.
[9]张智广.基于VIKOR 算法的供应商选择方法研究[J].甘肃联合大学学报(自然科学版),2012,26(5):27-29.
[10]孙文清.第三方物流供应商评价的实证研究——基于探索性因子分析与综合赋权法[J].中国流通经济,2014,(4):91-95.

