知其然,又知所以然
——对《形同质别的不等式恒成立与有解问题分析》补充
黄汝平
(福建省龙岩市高级中学 福建龙岩 364000)
知其然,又知所以然
——对《形同质别的不等式恒成立与有解问题分析》补充
黄汝平
(福建省龙岩市高级中学 福建龙岩 364000)
不等式恒成立与有解问题是高考的热点,又是学生学习的难点.怎样在理解的基础上,掌握其解决方法,是突破这个难点关键所在.否则易混淆、易错.因而需对问题的本质提示,区别各问题异同点.文中通过举例说明,帮助学生理解解题原理,再结合变式训练,使得学生切实理解并掌握.
热点 难点 原理 恒成立 有解
不等式恒成立与有解问题是高考的热点,又是学生学习的难点.有关这一问题的文章很多.文[1]中就不等式恒成立与有解问题,通过一个问题,比较系统归纳了五种有关不等式恒成立与有解的常见类型,并给予解法分析,同时得出了两个结论,最后再举了两个例子来说明,使学生对此问题有个清晰的认识,知道该怎么做,称之为知其然.本文想对此问题作个补充,不妨当作变式训练,记为变式1、2、3,并对这八个类型问题谈谈自己的认识, 为了让读者便于阅读和思考,仍以文[1]中所提出的问题加以说明,使学生明白为什么可以这样,可谓知所以然.
解法一.此类问题若能将参数k与x分离,一般首选分离参数法
解法二.若参数k与x不易分离,当 ]3,3[-∈x 时,转化为
而第二类就比较不好理解,尤其是问题(4)、变式1和变式3.前面谈到变式1是指时,函数与的图像有交点即自变量相同,函数值相同.而却不是,如图1,若作一条与y轴垂直的直线l,当l同时与函数与函数的图像有交点,则方程有解,否则无解.从集合角度看,函数的值域A与函数的值域B交集应满足.对于第二类问题其实质是研究集合A与B的关系.利用数轴能形象刻画它们二者的关系.在实际教学中,若能借助几何画板变换函数的图象效果会更好.我认为把满足这一条件,看成两图像有一样“高”的时候.那么满足看成“高矮“比较,学生会觉得形象、直观.在数轴上体现就是集合A与B关系.再看问题(4): 若对于任意总存在使得成立,就好理解为什么据函数、导数的知识先求出变式3: 若存在使得成立.可先研究此时通过容易得到或用补集法可得所求k的取值范围

图1
同学们可将上述的八个问题看成解这两类问题的原理,再举几个实例,供同学们参考.


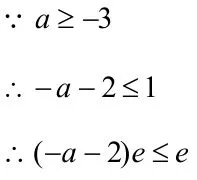
分析与略解:(Ⅰ)略
解:(1)略
[1]郑一平.形同质别的不等式恒成立与有解问题分析.数学通讯.2010(7)
黄汝平,中学高级教师,连续多年被评为"优秀班主任",发表论文多篇.

