物理学科中的微元法的解题应用探究

范梓锐

（湖南省长沙市明德中学 湖南长沙 410009）

物理学科中的微元法的解题应用探究

范梓锐

（湖南省长沙市明德中学 湖南长沙 410009）

我们在高中物理学习的过程中，要确保有非常清晰的逻辑思维，学习环节要有非常强的协调能力，因为物理学科的一些内容都存在较强的抽象性，理论与实际之间存在着较大的差异性，所以，学生在解题时通常都找不到头绪，而且现阶段高中物理题很多都较为复杂，涉及的知识面较广。学生解题能力的提高主要源于对概念规律的理解与运用。因此要引导学生通过最有效可行的方法去解题。

物理 微元法 解题 应用

一、“微元法”的基本概念

“微元法”是现阶段较为普及的一种解决物理问题的形式，此解题形式能够解决一些复杂的物理题，利用此方法去解决物理题能够把问题整体简易化。利用“微元法”去解决物理题时，要将问题整合为很多个十分微小的“元过程”，“元过程”对原题目予以拆分后，我们在解题环节，只需要对拆分出的“元过程”予以合理的分析，再将“元过程”中存在的物理思想予以相应的处理，进而去解决物理题中所给出的问题。通过“微元法”解决物理题时，我们要构建起必要的先决条件，此解题形式一定要把我们已获取的物理定律予以深化，再对其进行深入的思考，进而起到巩固知识、完善能力的作用。

“微元法”在解决物理问题时，主要分为下述几个环节：（1）明确分析对象，构建“微元”，（2）再把这一概念渗透到整体，根据物理规律建模同时予以求解，（3）去掉“微元”，得出普遍结果。

二、“微元法”解题的相关例子

1.应用于质量元.

关于质量元的物理题其中一些规律都是大同小异的。按照“微元法”的解题脉络，第一步我们要把问题予以拆分，得到一些小的质量元，在小的质量元中择取一个予以分析，在此基础上按照质量元间的联系对其予以全面分析，进而得出解题过程与题目的结果。

2.应用于电磁感应.

例1：如图1，水平放置的光滑平行导轨上放一质量为m的金属杆，导轨的距离是L，导轨的一边连接上阻值是R的电阻，不计其余电阻，磁感应强度是B的匀强磁场垂直在导轨平面，现给金属杆一个水平向右的起始速度，再让其进行运动，导轨无限长，求金属杆在导轨上向右移动的最大距离为多远？

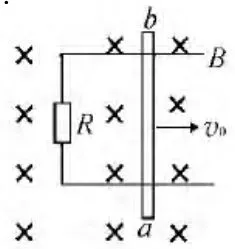
图1

图2

第一步我们要对此题目中的金属杆予以受力分析，见图1，在水平面上从a到h的方向来分析，金属杆会受到三个方向力的作用，其中受到的重力作用来自于竖、直、下，同时其受到竖直向上的支持力，还有电磁场予以金属杆水平向左的安培力，因此金属杆受到的是三个方向的力，同时三力没有制衡，金属杆所受的重力与支持力是相对平衡的力，唯一会让金

属杆出现位置改变的力就是安培力，因为安培力是变力，也就是金属杆做的是加速度降低的减速直线运动，利用已知的物理知识内容不可能解决此题，所以，我们要换一种模式进行解题。

3.应用于力做功.

将“微元法”晕用到物理的变力做功提之中，也是十分有效的解决物理变力做功问题的手段.

例3：若用一个强弱无变化的力F把某一物体按着一个半径为R的圆周运动，力F的作用方向是一直沿着切线的方向，怎样求解力F所做的功的多少？

求解力F做功的多少时，1X=FLcosa此公式只能够应用到恒力做功，因此此题不适用。若按照“微元法”的解题方式先对此题目与问题予以分析，在实际的情况中，因为力F的方向与物体的运动方向相统一，所以，变力F为动力做功，在此题目中，力F在一周圆周运动中的做功我们可以看作为正功.

根据“微元法”的概念我们能够将物体的曲线圆周运动问题分解为很多△L的“元过程”，同时因为这些小元段属于无限小，所以，能够将这些小元段看做是直线，这样我们就能够将变力F的做功变为恒力F做功，在此基础上按照功的恒力求解公式W=F.△L，再按照所有小元段的做功多少求解总的变力F的做功多少，此题的公式为：

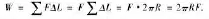
通过上述公式就可以求出变力F做功的多少了。

“微元法”是一种极限化的形式，“微元法”以对微小变量的研究为先决条件，根据数学中的极端思想和叠加概念，进而延伸出常规形式无法直接求出的结果.

［1］.杨宝山；我国高中物理课程教学大纲变革的历史回顾［A］；纪念《教育史研究》创刊二十周年论文集（4）——中国学科教学与课程教材史研究［C］；2011，14（08）：798-799.