运用几何画板提效解题教学*——以动态几何题中重叠图形面积的计算为例

☆谢登峰 唐剑岚

（广西师范大学数学与统计学院，广西桂林541004）

运用几何画板提效解题教学*——以动态几何题中重叠图形面积的计算为例

☆谢登峰 唐剑岚

（广西师范大学数学与统计学院，广西桂林541004）

动态几何题是中考的热点题型，“动”已成为中考眩目的亮点。但由于动态几何题的教学难度较大，学生往往十分畏惧解答这类题型，教师在教学解题思路时也受到限制。而几何画板具有数学视觉化和动态化的功能，能够提升此类问题的教学效果，有助于培养学生的分析能力和想象能力。本文以动态几何题中重叠图形面积的计算为例，探讨利用几何画板如何提升解题教学的效率。

几何画板；数学解题；动态几何题；重叠图形

一、多元表征，效果泾渭分明

重叠图形面积的计算问题，知识综合性强，条件不明显，结构相对复杂。采用传统教学方式对此类问题条件的标注和推理过程的呈现比较死板而滞后，且展示效果模糊，不利于反复呈现。而利用几何画板的标注、动画、移动、轨迹功能，不仅可以鲜明表征各种条件、结论，还可以动态显示各种数量关系，表征方式多样，显示效果突出。

例1：如图1，在矩形ABCD中，AB=9，AD=3 3，点P是边BC上的动点（点P不与点B，点C重合），过点P作直线PQ∥BD，交CD边于Q点，再把△PQC沿着动直线PQ对折，点C的对应点是R点，设CP的长度为x，△PQR与矩形ABCD重叠部分的面积为y。

（1）求∠CQP的度数；

（2）当x取何值时，点R落在矩形ABCD的AB边上；

（3）①求y与x之间的函数关系式；

②当x取何值时，重叠部分的面积等于矩形面积的7/27。

女儿读硕士班时，也同时走进婚姻。她初为人母，我一手看护新生儿，让她安心完成硕士论文的写作。论文口试时，我推着婴儿车陪考，一路照顾宝宝，论文答辩终于完美过关。她出书，废寝忘食地赶工，受邀到法国各地参加书展，出席各种签书促销活动，我都义不容辞地包揽了照顾幼儿的重任！

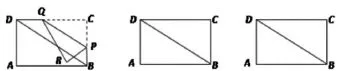
图1　

此题涉及图形的运动、轴对称、直角三角形、二次函数等数学知识。解决此题的突破点是把轴对称问题化归为运动问题，难点是寻找Rt△QRP与矩形ABCD重叠部分图形形状变化的临界点。根据题意，需要作出Rt△QCP的轴对称图形Rt△QRP。在传统教学方式中，教师使用尺规作图法，不仅耗费时间，而且不便于展示Rt△QRP的多种可能性，为寻找图形变化的临界点，教师一般会频繁提示，不断重复，造成了课堂的低效。而使用几何画板，教师通过简单操作就可以动态展示图形临界情况，并且通过属性设置，还可以用颜色区分变化前后的图形。使用多种表征方式刺激学生的视觉，增强了区分度，显示效果更加形象生动。

如图2、图3所示，根据题意构造矩形ABCD，AB=9，AD=3 3。构造线段CB边上的动点P，点P为主动点。过点P作PQ平行DB，双击PQ，作出点P关于PQ的反射点R，很便捷地作出Rt△QCP的轴对称图形Rt△QRP，拖动点P，不同的位置形象地体现了折叠的各种可能性。

图2　

图3　

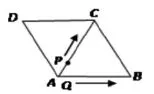
图4　

学生能较直观地看到图形变化的分界点，从而促进学生逆向思考分界点的位置，再通过计算可快速得出自变量的取值范围为0＜x≤2 3和2 3＜x＜3 3。

相比传统的尺规作图法的教学，使用几何画板能更容易地找到动点P的临界点，再通过度量此时线段CB的长度，可以轻松估算出x的值，还可以通过设置临界点前后图形的不同颜色，使呈现的画面效果泾渭分明。

二、“无”中生“有”，结论如影随形

重叠图形的面积计算问题涉及运动、轨迹、函数、最值、方程等较为抽象、复杂的概念，各概念间的关系也较为含蓄。传统处理方法常常力不从心，而几何画板的合理应用，能做到“无”中生“有”，直观揭示隐含条件，并能使多元隐匿的关系直观化、动态化、明朗化，帮助学生全面地理解题意。

例2：如图4所示，菱形ABCD的边长为6cm，∠B= 60°。从初始时刻开始，点P、Q同时从A点出发，点P以1cm/s的速度沿A→C→B的方向运动，点Q以2cm/s的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P、Q两点同时停止运动，设P、Q运动的时间为x秒时，△APQ与△ABC重叠部分的面积为y平方厘米。

（这里规定：点和线段是面积为O的三角形）解答下列问题：

（1）点P、Q从出发到相遇所用时间是几秒？

（2）点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时x的值是几秒？

（3）求y与x之间的函数关系式。

本题涉及到图形运动、面积重叠、直角三角形、相似三角形、函数等相关知识，包含动点P、Q的相遇时间、等边三角形出现的阶段、分段函数的三种位置关系等结论。如果教师仅凭板书、尺规作图等方法讲解，在短时间内难以让学生发现这些结论。而使用几何画板可以轻松弥补以上短板。

如图5、图6、图7、图8所示，通过拖动点Q，引导学生直观感知点P和Q随着时间x的增加在C点相遇，从而易知时间相同，用点P的路程除以速度轻松算出时间为6秒；绘制点Q的轨迹，使点Q运动轨迹随时显现，从图6、图7的图像中可以清晰发现重叠面积的变化经历了三个过程，自变量x的取值区间分别是0≤x≤3、3＜x＜6、6≤x≤9，并且面积y的函数解析式也是不同的。

如图8，点Q在ABC运动时，可以看到∠PAQ始终小于60°，只有当6＜x≤9时，才会出现角∠PAQ=90°的情况。形象的动画可以直指问题核心，几何画板让画面真正动起来，避免了死板的作图和分析，可以大大节省讲授时间，学生也容易理解，大大地提高了课堂效率。

图5　

图6　

图7　

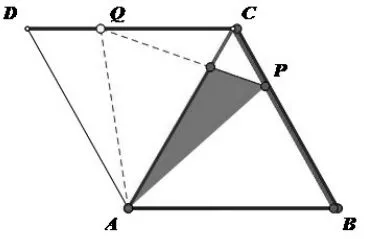
图8　

三、“动”“静”结合，感悟数学思想

数学课程标准实施后，数学的思想和方法成为了数学课程的重要内容，为了加强数学思想方法的教学，必须创设思想方法教学的条件。利用传统方法进行数学思想方法的教学时，总会遇到较多困难，如作图低效、画面单调晦涩，不能激发学生的兴趣等。而利用几何画板进行教学，不仅可以创设数学思想方法教学的环境（如数形结合），充分展示数学的思想与方法，揭示数学规律，把握数学的精髓，更容易让学生感悟问题中蕴含的丰富的数学思想［2］。

例3：如图9，在梯形ABCD中，AD∥BC，∠B=90°，BC=6，AD=3，∠DCB=30°。点E、F同时从B点出发，沿射线BC向右匀速移动。已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG。设E点移动距离为x（x＞0）。

（1）△EFG的边长是____（用含有x的代数式表示），当x=2时，点G的位置在____；

（2）若△EFG与梯形ABCD重叠部分面积是y，求：

①当0＜x≤2时，y与x之间的函数关系式；

②当2＜x≤6时，y与x之间的函数关系式；

（3）探求（2）中得到的函数y在x取何值时，存在最大值，并求出最大值。

图9　

图10　

如图10所示，拖动点F，度量线段BE的长度即自变量x的值，当值是2cm时，从图形上看出点G与点D重合，通过推理计算得出答案，体现了数形结合和一般到特殊的思想。通过动画演示，可以看出重叠部分图形面积的变化，依次经历了等边三角形→四边形→30°角的直角三角形三个过程，逆向思考可以得出需要分三类情况讨论，度量和计算验证可以得出自变量x的范围分别是0＜x≤2、2＜x＜3、3≤x≤6三种情况，体现了运动与变化的思想，分类讨论的思想等。

如图11，利用几何画板追踪动点E的运动轨迹功能，可以发现重叠部分面积是由小到大再变小，存在最大值，从坐标系可以清晰看到当自变量2＜x＜3时，有最大值。用两个三角形面积之差表示重叠部分的四边形的面积，列出二次函数，求出最值。此题体现了运动与变化的思想、数形结合思想、函数思想等。

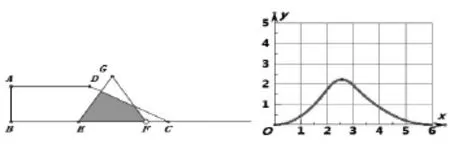
图11　

此类题目蕴含运动与变化的思想、一般到特殊的归纳思想、化归思想、数形结合思想、函数与方程的思想、分类讨论的思想等。传统的教学模式囿于作图过程繁琐、表现形式单一等因素的限制，难以吸引学生的注意力，反而成为学生形象思维发展到抽象思维的羁绊。而几何画板可以动态演示变化过程，追踪轨迹，展示静态图像，动静结合，相得益彰，学生更易于在数形结合中感悟丰富的数学思想。

总之，平面几何图形重叠图形面积计算问题具有较多难点，恰当应用几何画板，不仅可以轻松突破这些难点，还可以促进学生从元分析的视角理解和应用有关知识解决问题［3］。另外，根据笔者多年教学的经验，学生更喜欢使用几何画板这种有“科技含量”的课堂，更乐于参与这样的教学活动，所以，几何画板是高效课堂不可缺少的“利器”。

［1］唐剑岚.计算机辅助数学教学原理与实践［M］.北京：清华大学出版社，2012：33.

［2］邢方.多媒体信息表征呈现形式对学习效果的影响研究［J］.中小学信息技术教育，2014，（15）：130-131.

［3］王丽娜.元分析视角：支持数学问题解决的技术工具研究［J］.中小学信息技术教育，2015，（12）：65-68.

［4］王波.用几何画板的轨迹功能探讨数学问题的解法［J］.数学通报，2008，（11）：19-22.

［5］欧慧谋.动态视觉化技术及其对数学概念教学的作用［J］.中国教育技术装备，2011，（27）：37-39.

*本文是2013年度广西高等教育教学改革工程项目（2013JGZ113）、广西教育科学“十二五”规划广西普通高中课程改革专项课题（2013ZJJ048）的部分成果。

［编辑：陈钺］

G434

A

1671-7503（2015）21-0057-03