光学陀螺随机误差特性的混合理论方差方法分析

汤霞清，程旭维，高军强

（装甲兵工程学院控制工程系，北京100072）

光学陀螺随机误差特性的混合理论方差方法分析

汤霞清，程旭维，高军强

（装甲兵工程学院控制工程系，北京100072）

为更有效地测试和分析光学陀螺的随机误差特性，提出采用混合理论方差（TheoH）的方法全面表征和分析陀螺输出数据。该方法建立在Allan方差和去偏的#1理论方差（Theo1）的基础上，解决了Allan方差计算的平均时间只能够达到数据持续时间长度的一半，以及长相关时间下置信度下降的问题，同时构造的新方法能够自动去除Theo1方差相对于Allan方差的偏差。对比分析了新方法对白噪声特性以及光纤陀螺实测数据中随机噪声的类型和噪声水平的辨识结果。实验结果表明，通过去除偏差和提高方差估计的置信度，新混合理论方差方法对估计各种白噪声以及长相关时间下光纤陀螺噪声特性提取更有效，精度更高，同时能够兼容Allan方差对量化噪声、角度随机游走、零偏不稳定性、速度随机游走、速率斜皮5种噪声进行无偏估计。

兵器科学与技术；惯性导航系统；陀螺；#1混合理论方差；随机噪声

0 引言

近年来，激光陀螺和光纤陀螺技术蓬勃发展，并在惯性导航、制导领域得到广泛应用。陀螺仪的精度很大程度上决定着惯性导航系统的精度，在光学陀螺的研制和使用中，不可避免地需要对陀螺各项性能进行测试分析并进行客观、准确的评价，然后通过适当的手段进行误差补偿以提高系统精度［1-2］。

N秒平均法与Allan方差法（Avar）是两种常用的光纤陀螺随机误差性能评价方法。文献［3］对二者之间的内在关系进行了详细分析。Avar方差法是IEEE标准化组织推荐用来评价和测量光学陀螺随机噪声特性的特定方法［4］。但其存在两个固有缺陷:对于有限长的数据，估计置信度依赖于数据的独立组数，估计误差随数据独立组数的减小而增大［5］；Avar计算的平均时间只能够达到数据持续长度的一半，长相关时间下估计置信度较差。另外，类似于无窗的离散傅里叶变换，转移函数的泄露现象［6］也是其潜在的问题。相比于Avar及其改进、总方差［7］、Hadamard方差［8］以及动态Allan方差［9］等统计方法，#1理论方差法（Theo1）［10］具有最优的置信度，因此估计精度最高，但因其采样方式的不同而导致估计结果存在偏差。

结合Allan方差和Theo1的优势，并弥补二者各自的不足，本文采用一种新的混和方差方法（TheoH）来研究光学陀螺的随机误差特性。TheoH是一种较新的用于时频稳定性分析的统计方法，由美国国家标准与技术研究所的Howe［11］首次提出，主要用来研究震荡器的频率稳定性，如原子钟频率稳定性的检测。该方法一方面保持了Theo1方法的优势，同时完全兼容Avar.其通过等效自由度（EDF）的提高增加了估计结果的置信度；同时，计算的数据长度比常规的Avar增加了50%，完全解决了Avar面临的两个难题，但其仍处于发展之中，主要原因是其EDF的求取还未形成统一的数学形式。

本文利用TheoH分别分析白噪声和光纤陀螺噪声特性，通过求取去偏前后的混和方差对各种幂律噪声的辨识结果，并与Avar和Theo1的结果进行比较，分析了TheoH在分析光学陀螺噪声时的优势，这些独特性质对于实际应用中提高陀螺性能设计和动静态误差补偿具有指导意义。

1 Avar和Theo1方差分析

1.1 Avar

建立在时域上的Avar分析法能够轻易辨识和表征光学陀螺中的各项随机误差。利用其与功率谱密度（PSD）之间的定量关系，可直接从时域上得出陀螺仪各误差源的类型和幅度。关于Allan方差的基本过程可描述为:

利用新的样本序列xj（m），定义时域上的Avar方差为

式中:δj=xj+1（m）-xj（m）为相邻数组均值之差；〈〉表示总体均值。通过选取不同的值（即相关时间），即可求得相应的Avar以及标准差。在实际计算中，通常采用其估计值的形式:

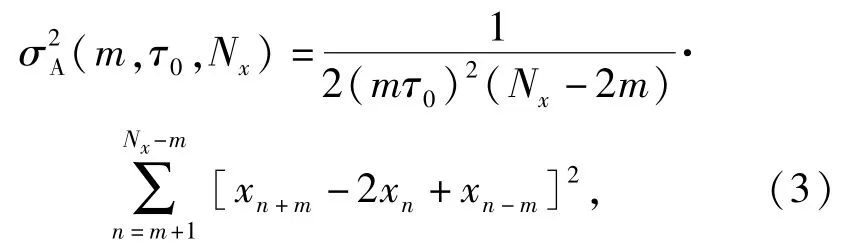
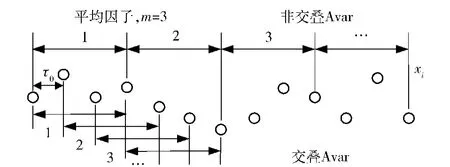
图1 非交叠和交叠的Avar采样过程Fig.1 Sampling process of non-overlapped and overlapped Avars

二者的区别在于产生新序列时，常规Avar直接将原始信号分为m组，然后求均值；而交叠式Avar在各个数据点上以m为相关长度进行窗口滑动，然后对分组后的数据求取均值。

Avar的估计是针对有限长度数据的，其估计的可信度完全依赖于数据的独立组数。对于独立组数为k的随机信号，估计的可信度随k的增加而提高，Avar估计的百分比误差可表示为

例如，当总数据点数Nx=7 200时，若每个子集包含m=100个点，即k=72，其估计误差为8.40%.

1.2 Theo1

#1理论方差方法是一种类似于Avar的分析方法，其采用了步幅更宽的二次采样过程，性能更优。由于实际的测量值均是离散的，因此对于给定的时间序列｛x（i）|i=1，2，…，Nx｝，相邻观测值之间的采样周期同样为0，给出其定义式为

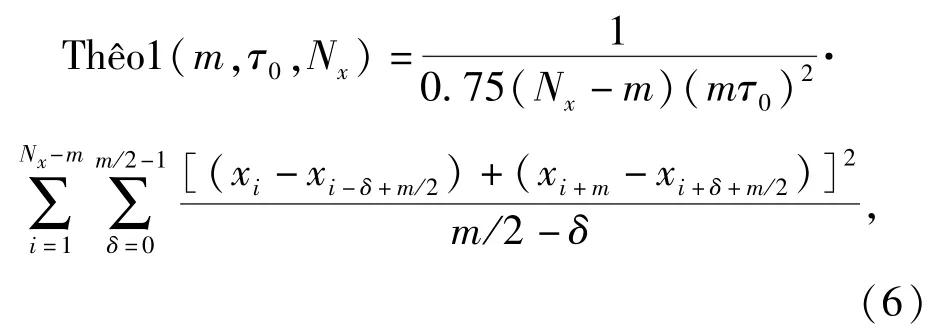
式中:m=2，…，Nx-1，且为偶数；平均采样时间的步幅为可见:对于长度为Nx的样本序列，最后一个相关时间为s=0.75（Nx-1）0，即平均相关时间接近总数据长度的3/4，而在Avar的计算过程中，该值只能达到Nx/2，即比Avar长50%.

当m较小时，并不能完全体现Theo1在这方面的优势；但在测量长相关时间的频率稳定性时，为得到较大m，通常在原始数据采集过程中，尽量使0更小以获得更多原始数据。这样才能有效分离更多关于噪声类型的信息。考虑到可置信度对结果的影响［12］，通常设定10≤m≤Nx-1.

图2描述了在（6）式中，Theo1通过在区间T上，求取在不同的平均相关时间1，2，etc及对应变步长s1，s2，etc下的测量信号yn=（xn-xn-1）/0的各项差分，即等效的平均相关时间s值在区间［T/2，T-0］上变化时，得到对信号yn进行二次采样的过程。即通过选取不同平均因子求得各项的差分。当δ= 0时，采样步长s1=1=T/2，此时（6）式退化为经典的Avar，如图2（a）中所示；图2（b）中所描述的是（6）式中1＜δ≤m/2时，累加和的中间项的采样函数，此时采样步长为T/2＜s（·）＜T-0；图2（c）中所示为（6）式中累加和的最后一项的采样函数，此时s（N）=T-0.

图2 Theo1变步长的采样过程Fig.2 Sampling process at varible step length in Theo1

2 新的混合理论方差

由于Theo1采用的数据采集方法和Avar不同，使得二者之间存在显著偏差。二者之间的这种偏差以比率形式可表示为

文献［13］利用蒙特卡洛方法对（7）式中的偏差和m之间的关系进行了拟合，得到:

式中:a、b、c均为常数。5种常规噪声——调频白噪声（WHFM）、调频闪烁噪声（FLFM）、调频随机游走（RWFM）、调相白噪声（WHPM））和调相闪烁噪声（FLPM）分别对应的Theo1和Avar偏差值如表1所示。此处需要特别注意的是，除了对WHFM是无偏估计外，其余噪声均存在偏差。

表1 Theo1偏差函数中的常值系数Tab.1 Coefficient of the bias functions of Theo1

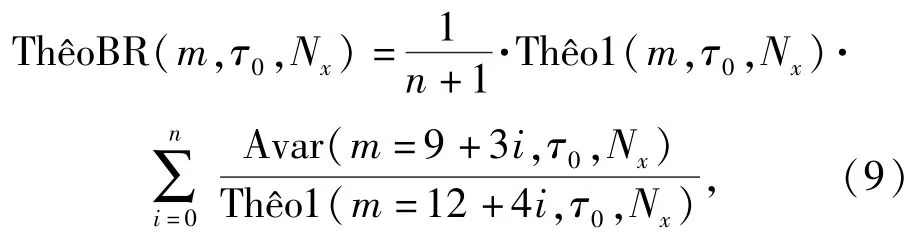
式中:n=floor（0.1Nx/3-3）；Avar和Theo1的定义如（3）式和（6）式所述。为防止在长相关时间下Avar的置信度下降，选择值在数据总长度的一定比例之内（如选择值为10%～20%的数据总长度）。

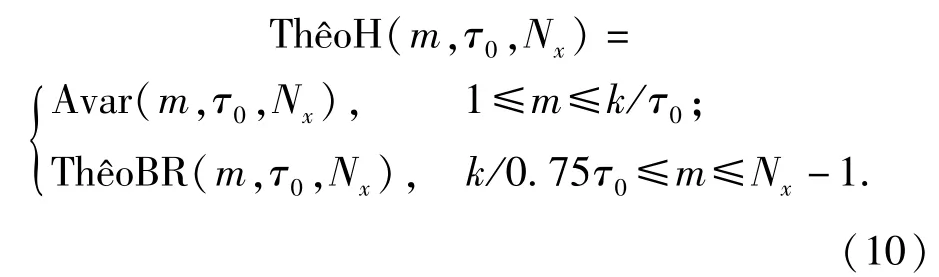
3 光学陀螺的随机误差特性分析

光学陀螺自身因素以及外界环境的干扰外界如光强变化、热效应等工作环境因素影响，使得陀螺输出中包含各种复杂的随机噪声，直接从物理意义出发建立准确的随机噪声误差模型比较困难，因此采用PSD函数来定义各类噪声。其中包括量化、角度随机游走噪声等，虽然还存在少量正弦以及其他类型噪声［14］。运用新构造的TheoH方法一方面可定性地辨识出光学陀螺中各噪声类型；同时，可以计算各类噪声的噪声水平。

考虑到与Avar与PSD之间的关系［15］，同时假设陀螺各噪声在统计意义上互不相关，且分布于不同频段上，将TheoH表示为5类噪声的平方和，即

考虑到表1中Theo1与Avar之间存在的偏差，将得到不同于Avar的拟合系数:

式中:an为TheoH所确定的各噪声项方差拟合系数。

图3 ～σ2双对数图Fig.3 log-log plot of～σ2

由于Avar自由度较小而导致结果波动较大；而Theo1具有相对较大的EDF，从而使得估计置信度最大，可以代替Avar对光学陀螺进行长相关时间的性能分析；同时可评价随机噪声建模仿真以及滤波效果，很好地解决了长期测试过程中频率稳定性的问题。TheoH继承了Theo1在长相关时间下的自由度，同样为非整数，以10%的拟合精度给出其EDF的计算式为

值得注意的是，在进行频率稳定度估计时还须给出估计值的置信度。TheoH的EDF取决于Nx和s.在对置信区间进行估计时，采用χ2分布函数。百分比误差ΔTheoH（）与EDF的之间的关系为

式中:EDF≥1，此时（13）式能够给出90%置信区间内Thêo1（0.75m0）的百分比误差。通过仿真比较3种噪声对应的Theo1的EDF和百分比误差，采样点数选择为7 200时的结果如表2所示。

表2 #1理论方差下3种噪声等效自由度以及百分比误差Tab.2 Equivelent degress of freedom and percentage errors of noises of Theo 1

4 实验结果及讨论

TheoH能够完美地给出随机过程以及光学陀螺中的各种噪声，通过分析双对数图中对应的曲线可以检验噪声类型并辨识出噪声参数。实验设计过程中首先利用白噪声，通过与Avar以及Theo1来对比验证TheoH的优越性；然后利用TheoH测试实测光纤陀螺输出数据，拟合得到陀螺仪中各项随机噪声参数。

1）仿真验证。对比静态高斯白噪声和方差时变噪声（通过改变与白噪声方差或标准差）在整个数据段上的Avar和Theo1特性。结果如图4～图7所示。

图4 静态高斯白噪声Fig.4 Stationary white Gaussian noise

图5 静态高斯噪声的Allan方差和#1理论方差（双对数）Fig.5 Allan variance and Theo1 of stationary white Gaussian noise

从图5和图7中可见，在分析纯白噪声和方差时变噪声的频率稳定性时，Avar无法完全表征噪声特性，尤其在m值较大情况下，结果波动较大且不稳定性；而采用Theo1在整个数据段上的分析频率稳定性时性能优越，尤其在较大m值下，Avar无法给出可信结果，而Theo1依旧能够给出高置信度结果。在数据总长度为7 200的情况下，最后一个相关时间约为5 400，比Avar中最长的值（3 600）大50%。所以当采样数据较少时（如10%T），即短期相关时间内，Theo1和Avar方差效果相当；在长相关时间分析上，由于Theo1具有较高的EDF，能够得到更精确的结果。

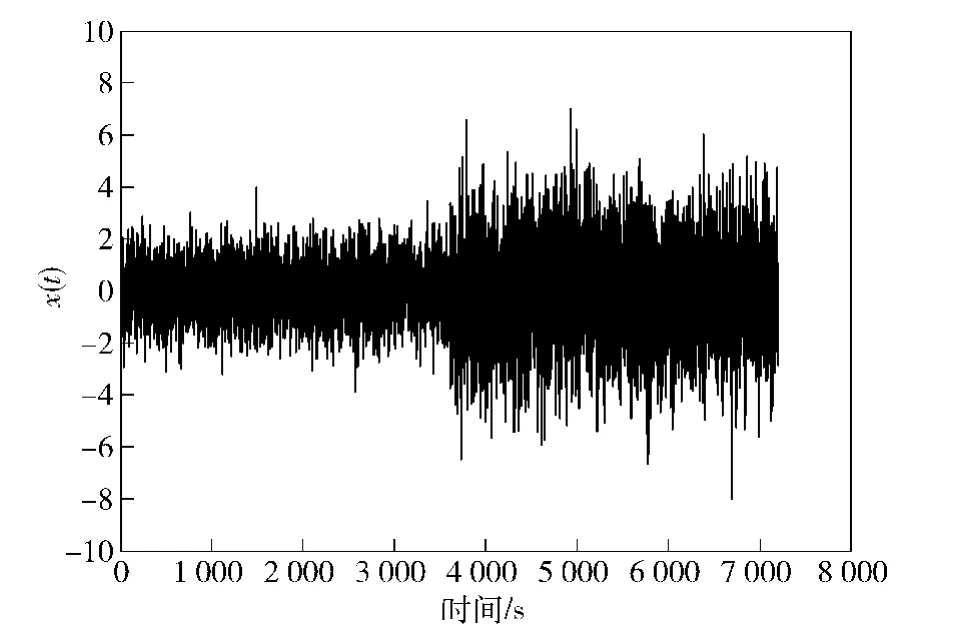
图6 方差时变噪声Fig.6 Noise with the time-varying variance

图7 方差时变噪声的Allan方差和#1理论方差Fig.7 Avar and Theo1 of noise with time-varying variance

在分析纯白噪声时，Avar和Theo1均是无偏的，但对于方差时变噪声，Theo1出现了少量偏差，该偏差在分析光学陀螺数据时具有明显体现。

2）光学陀螺数据验证。由于激光陀螺的测试过程类似，此处仅以光纤陀螺为例验证TheoH的优越性。在实验室室温下采集光纤陀螺的数据时，首先将某型号的惯性测量单元（IMU）固定于高精度转台上，并保持转台水平，由于光纤陀螺传感器的输出频率保持在10 Hz以上，采样周期设定为10 ms（即以100 Hz输出），采集2 h的数据（720 000个数据）。

实际上，由于较大的采样频率获得了更多信息量的数据，因此可更加明显地验证TheoH相对于Avar的优越性。为了对应于前面的实验，且仅以说明该新方法的优越性为目的，在原始数据采集之后，对所获得的数据进行1 s的平滑，可得到更加直观的结果，此时0=1 s.这里值得注意到的是:数据预处理并不影响该方法的适用性，因为其针对采样后的数据点进行操作，所以结果仍会更优；再者，在实际应用中，传感器原始数据的采集过程中通常需要经过平滑处理再进行误差消除以及后续解算。因此，以0=1 s的形式给出结果更直观。

数据采集并进行平滑处理后，分别计算Avar、Theo1和TheoH，并辨识和估计出光纤陀螺的主要误差类型和相应的随机噪声参数。图8为光纤陀螺的实测输出数据，图9分别比较了光纤陀螺输出数据的Avar、Theo1以及TheoBR结果，并以双对数结果给出。进行最小二乘拟合得到的各种类型噪声系数如表3所示。

图8 光纤陀螺输出信号Fig.8 Output signal of FOG

图9 光纤陀螺输出的Avar，Theo1和TheoBR方差（双对数）Fig.9 Allan and Theo1 analysis of FOG's output（log-log）

表3 各种类型噪声系数Tab.3 Noise coefficients of FOG

从图9中可以看到:在短期相关时间内，Theo1和Avar均具有良好的线性特性，且都具有无偏性；而相关时间较大时，Avar出现较大的波动，估计值变化剧烈，估计误差较大，这是因为当=T/2时自由度下降为1，而此时因为数据对称的缘故使得其处于“崩溃”境地，而TheoH由于自由度较高，使得方差估计的置信度有所提升，因此其能够更加精准地描述陀螺仪的零偏不稳定性、速率随机游走、速率斜坡3个参数，而Avar表针的此3个参数的结果波动较大，且不具备线性性，即TheoH解决了Avar这方面的不足；同时，良好的线性度使得TheoH更易通过最小二乘拟合的方式得到各噪声项系数，并更精确地刻画幂律噪声特征。

图10给出了消除Theo1与Avar之间的偏差后的TheoH双对数结果，一方面TheoH方差结果与相关时间在双对数图中的线性关系更加突出；同时结果更加平滑，并未出现Avar结果的巨大波动和不稳定性，即使用TheoH能够更加简洁有效地描述陀螺各项噪声。

图10 光纤陀螺输出的混合理论方差（双对数）Fig.10 TheoH analysis of FOG's output（log-log）

最后，从辨识结果可以看出，该型号光纤陀螺的误差主要表现为量化噪声、速率斜坡以及角度随机游走，在设计、生产和使用过程中采取相应的措施降低这些噪声带来的影响，既可提高系统精度。

实验结果表明:TheoH在分析光学陀螺性能时，对任意大的值是有效的，包括3/4的全部数据采样时间长度，利用该方法在整个数据段上得到的置信度比Avar高；通过去偏构造的TheoH在～σ2双对数图上清晰地保持了μ=-α-1（α为噪声频率指数）的线性关系，这样使得幂律噪声更易表征和提取，尤其是针对光学陀螺的零偏不稳定性、速率随机游走、速率斜坡等参数的辨识更精准。因此，该方法能够针对整个数据段上的光学陀螺进行误差特性，其可代替Avar成为更优良的光学陀螺误差特性分析工具。

5 结论

针对传统的Allan方差在分析光学陀螺随机噪声特性时出现的不足，本文提出利用TheoH方法来分析光学陀螺随机噪声特性。利用静态和时变高斯白噪声以及光纤陀螺实测数据验证新方法的优势。结果表明TheoH方法具有更高的估计置信度的同时，能够在短相关时间内完全兼容Avar；不仅能从时域上更准确地辨识出光学陀螺随机噪声的类型和噪声水平，且能够在整个数据段上对光学陀螺的噪声参数进行精确估计、对随机建模与仿真以及滤波效果评价。对工程中光学陀螺仪的设计生产和性能评估具有指导意义，尤其对高精度（如导航级）的光学陀螺的测试和性能评估更加重要。

（

）

［1］ 吴有龙，王晓鸣，曹鹏.抗差估计及Allan方差在车载组合导航系统中的应用研究［J］.兵工学报，2013，34（7）:889-895. WU You-long，WANG Xiao-ming，CAO Peng.The application of robust estimation and Allan variance method in land vehicle navigation［J］.Acta Armamentarii，2013，34（7）:889-895.（in Chinese）

［2］ 汤霞清，程旭维，郭理彬，等.小波分析和灰色神经网络融合的光纤陀螺误差建模与补偿［J］.中国激光，2012，39（10）: 1008003. TANG Xia-qing，CHENG Xu-wei，GUO Li-bin，et al.Error modeling and compensating of fiber optic gyro based on wavelet analysis and grey neural network［J］.Chinese Journal of Laser，2012，39（10）:1008003.（in Chinese）

［3］ 吕品，刘建业，赖际舟，等.光纤陀螺的随机误差性能评价方法研究［J］.仪器仪表学报，2014，35（2）:412-418. LYU Pin，LIU Jian-ye，LAI Ji-zhou，et al.Research on the performance evaluation methods of fiber optical gyro stochastic errors［J］.Chinese Journal of Scientific Instrument，2014，35（2）: 412-418.（in Chinese）

［4］ IEEE STD.IEEE standard specification format guide and test procedure for single-axis interferometric fiber optic gyros［S］.New York:The Institute of Electrical and Electronics Engineers，1998.

［5］ 王新龙，杜宇，丁杨斌.光纤陀螺随机误差模型分析［J］.北京航空航天大学学报，2006，32（7）:769-772. WANG Xin-long，DU Yu，DING Yang-bin.Investigation of random error model for fiber optic gyroscope［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32（7）:769-772.（in Chinese）

［6］ 高玉凯，邓正隆.基于小波方差的光学陀螺随机误差特性研究［J］.中国惯性技术学报，2004，12（5）:65-70. GAO Yu-kai，DENG Zheng-long.Investigation on random error properties of optic gyro based on wavelet variance［J］.Journal of Chinese Inertial Technology，2004，12（5）:65-70.（in Chinese）

［7］ 韩军良，葛升民，沈毅.基于总方差方法的光纤陀螺随机误差特性研究［J］.哈尔滨工业大学学报，2007，39（5）:708-711. HAN Jun-liang，GE Sheng-min，SHEN Yi.Research on the random error properties of FOG based on total variance［J］.Journal of Harbin Institute of Technology，2007，39（5）:708-711.（in Chinese）

［8］ Howe D A.The total deviation approach to long-term characterization of frequency stability［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2000，47（5）:1102-1110.

［9］ Lorenzo G，Patrizia T.The dynamic Allan variance［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2009，56（3）:450-464.

［10］ Howe D A.Method of improving the estimation of long-term frequency variance［C］∥The 11th European Frequency and Time Forum.Neuchatel，Switzerland:Swiss Foundation for Research in Microtechnology，1997:91-99.

［11］ Howe D A.TheoH:a hybrid，high-confidence statistic that improves on the Allan deviation［J］.Metrologia，2006，43（4）: 322-331.

［12］ Tasset T N，Howe D A，Percival D B.Theo1 confidence intervals［C］∥Proceedings of the 2004 IEEE International Frequency Control Symposium and Exhibition.Montreal，Quebec，Canada: IEEE，2004:725-728.

［13］ Howe D A，Tasset T N.Theo1:characterization of very longterm frequency stability［C］∥Proceedings of 18th European Frequency and Time Forum（EFTF 2004）.Guildford，UK:the Institution of Electrical Engineers，2004:581-587.

［14］ 李京书，许江宁，查峰，等.基于6类噪声项拟合模型的光纤陀螺噪声特性分析方法［J］.兵工学报，2013，34（7）: 835-839. LI Jing-shu，XU Jiang-ning，CHA Feng，et al.Analysis method for the noise characteristics of fiber optic gyroscope based on fitting model of six noise items［J］.Acta Armamentarii，2013，34（7）:835-839.（in Chinese）

［15］ El-Sheimy N，Hou H Y，Niu X J.Analysis and modeling of inertial sensors using Allan variance［J］.IEEE Transactions on Instrumentation and Measurement，2008，57（1）:140-149.

Hybrid Theoretical Variance Analysis for Random Error Properties of Optic Gyroscope

TANG Xia-qing，CHENG Xu-wei，GAO Jun-qiang
（Department of Control Engineering，Academy of Armored Force Engineering，Beijing 100072，China）

For the sake of testing and analyzing the random error properties and identifying the noise amplitude of optic gyroscope more effectively，a new hybrid theoretical variance（TheoH）strategy is proposed to analyze the gyroscope output，which is integrated with the Allan variance and theoretical variance#1 with auto-bias removal.The problems of that the averaging time calculated with Allan variance is half of total data length and the confidence decreases at long-term averaging time are perfectly solved. A new method for analyzing the random error properties of optic gyroscope is proposed.The proposed method is compared with the Allan and theoretical variance#1，and the noise types and noise levels of white noises and real gyroscope output are identified.The experimental results show that the TheoH can improve the confidence efficiently and has higher evaluation precision than the conventional Allan method in long-term τ-values.

ordnance science and technology；inertial navigation system；optic gyroscope；theoretical variance#1；random noise

V249.32+5

A

1000-1093（2015）09-1688-08

10.3969/j.issn.1000-1093.2015.09.013

2014-12-22

军队科研计划项目（51309030106）

程旭维（1989—），男，博士研究生。E-mail:chengxuwei0872@126.com；汤霞清（1965—），男，教授，博士生导师。E-mail:tangxiaqing_001@163.com