三相软件锁相环在便携式IEC 61850测试装置中的应用

吴振杰 符光辉 吴 靖 陶 涛

（1. 国网浙江省电力公司杭州供电公司，杭州 310009；2. 成都天进科技有限公司，成都 610041）

随着电子式互感器及合并单元技术的应用[1-2]，原来的交流回路由采样值光纤网络取代，不仅解决了TA二次回路开路、短路、多点接地问题和TV二次回路短路、中心线开路问题，还通过采样值网络断线闭锁保护技术解决了交流回路断线造成保护误动的问题[3]。但是以往具体的二次接线将由相互高度耦合、抽象的网络数据流代替，检修运行人员必须借助于智能化仪器仪表才能正确解读采样值网络信息，开展有效运维。

由于合并单元采用的是等间隔采样技术（假设电网频率始终为50Hz，每周波采样80点），如图1所示。当电网频率发生偏移时，由于傅里叶算法的频谱泄漏问题，会导致幅值及相位测量精度急剧下降，以致引起运行人员的错误判断，影响设备检修维护的效率和质量。本文针对此问题，就便携式IEC 61850测试装置采样值等间隔采样精度提升问题开展了研究。

1 等间隔采样与频谱泄漏

1.1 等间隔采样技术

无论对于采用网采模式（经过交换机网络传输）或直采模式（通过直连光纤传输）的采样值传输方式，合并单元均采用等间隔采样技术对模拟信号进行数字化处理[4-5]：在电网一次电流与电压通过常规或非常规互感器进行变换后，合并单元按照固定的4000Hz采样率对电流和电压信号进行采样及模数转换（对于电子互感器采样重采样），使用 IEC 61850-9-2协议以250μs等间隔通过网络报文发送给智能保护、测控、便携式数字万用表等智能电子装置。

1.2 频谱泄漏原因及影响

在进行离散傅里叶变换时，实际上是将被采样信号以采样长度为周期在时域进行周期性无限延拓而作为周期信号处理的。当采样长度不等于信号周期的整数倍时，在重复的拼接处会发生不连续，这种不连续性愈大泄漏就愈严重[6]。只有当采样长度等于信号周期的整数倍时，在重复的接头处衔接连续平滑，才不会造成泄漏。从频域角度分析，在被分析信号中只有等于分辨带宽整数倍的频率分量才没有频谱泄漏，而位于非分辨带宽整数倍的频率分量都会发生频谱泄漏。

对于采样值网络，通常假设电网频率为fn=50Hz，则合并单元采样频率固定设定为fs=fn×80=4000Hz，理论上由于采样频率是电网频率的整数倍，因此不会造成频谱泄漏。但事实上，电网的频率无法严格保持50Hz，当电网频率偏离50Hz时就造成了傅里叶分析产生频谱泄漏，而且偏离越大，则频谱泄漏越严重。

2 基于三相软件锁相环的等间隔采样频率跟踪及重采样算法

2.1 等间隔采样频率跟踪及重采样算法流程

本文提出等间隔采样频率跟踪及重采样算法解决频谱泄漏问题。首先使用三相软件锁相环动态跟踪电网频率，然后根据实际电网频率运用重采样技术对合并单元输出的采样值序列进行重采样，从而有效地避免频谱泄漏对离散傅里叶计算幅值和相位精度的影响，其流程如图2所示。

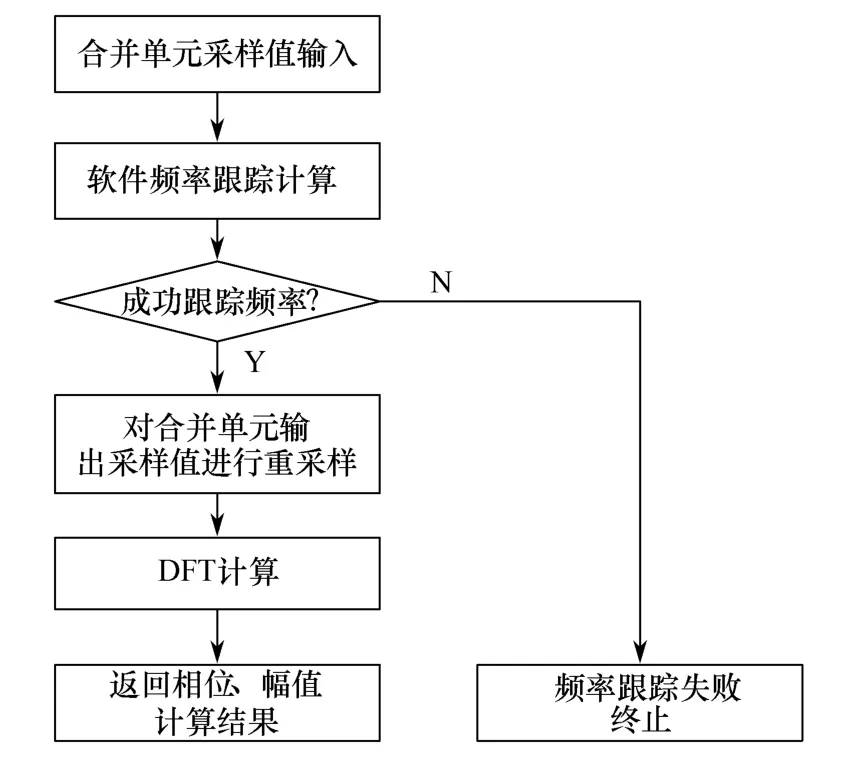
图2 等间隔采样频率修正算法流程框图

2.2 三相软件锁相环

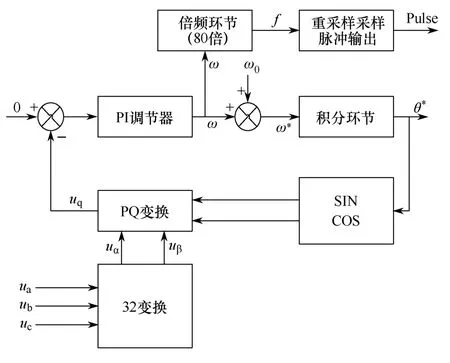
图3 三相软件锁相环示意图

本文所采用的三相软件锁相环基于瞬时无功理论[7]，如图 3所示。其基本原理是将三相输入电源电压ua、ub、uc转换到α-β坐标系中，得到uα、uβ，再经过pq变换得到uq、uq表示输入电压相位θ和锁相环输出电压相位θ*的差值，uq与0的差值经过一个PI调节器（比例积分）调节后得到误差信号ω，再与扰动角频率ω（基波角频率，确保在掉电的情况下仍然能够输出基波频率的正弦信号）得到角频率ω*，最后经过一个积分环节得到最终输出的相位ω*。三相软件锁相环是一个负反馈，通过PI调节器达到锁相的效果。在频相位完全捕获的情况下，ω实际频率=ω，而φ=0，经过倍频环节后以电网实际频率为基础输出每周波80点的重采样脉冲信号。

2.3 重采样技术

重采样处理方法是：在通过三相软件锁相环准确获得电网频率后，从整秒开始，以80倍电网实际频率的采样频率对合并单元输出采样序列进行重采样。若重采样点与合并单元输出采样序列不重合（事实上，大部分重采样点与合并单元输出序列是不重合的），则使用两点插值算法（也可采用多点插值算法进一步提高精度）进行插值计算，如图4及式（1）所示。

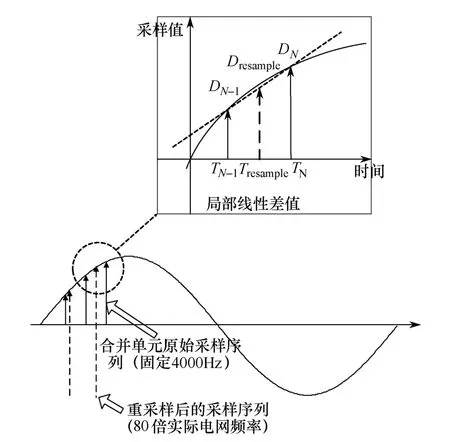
图4 重采样技术示意图

3 仿真计算分析

本文基于Matlab软件搭建了如图5所示的仿真测试平台，模拟电网系统频率从25Hz变化至75Hz的情况下合并单元采用 4000Hz等间隔采样的采样值输出。并分别就直接使用DFT算法和经过三相软件锁相环等间隔采样频率跟踪及重采样后再使用DFT算法两种计算流程进行了仿真计算和比较分析，详细结果如图6所示。

可见随着系统频率偏移 50Hz越远，直接使用DFT算法的幅值计算误差越大，而相位误差变化则更为剧烈，与 1.2节分析结果一致。而对采样值进行频率跟踪及重采样后再使用DFT算法，其幅值和相位计算值与设定值非常接近，试验结果表明能够确保频率在 30～70Hz范围变化内，幅值测量精度达到 0.01%，相位测量精度达到 0.01°，满足工程应用的需求。

图5 仿真测试平台

图6 仿真测试结果比较

4 结论

本文所提出的等间隔采样频率跟踪及重采样算法能够有效地解决由于电网频率变化导致的傅里叶计算频谱泄漏问题，显著提高傅里叶计算的幅值及相位精度，具有广阔的工程应用前景。

[1] 乔小敏, 董鹏. 智能电网及数字化变电站关键技术探讨[J]. 电气应用, 2011(7): 42-45.

[2] 高翔. 数字化变电站若干关键技术研究[D]. 杭州:浙江大学, 2008.

[3] 窦晓波. 基于 IEC 61850的新型数字化变电站通信网络的研究与实践[D]. 南京: 东南大学, 2006.

[4] 易永辉. 基于 IEC 61850标准的变电站自动化若干关键技术研究[D]. 杭州: 浙江大学, 2008.

[5] 时雷春. 基于 IEC 61850的变电站过程层采样值传输[D]. 北京: 华北电力大学, 2006.

[6] 江道灼, 孙伟华, 陈素素. 电网相量实时同步测量的一种新方法[J]. 电力系统自动化, 2003, 27(15):40-44.

[7] 李彦栋, 王凯斐, 卓放, 等. 新型软件锁相环在动态电压恢复器中的应用[J]. 电网技术, 2004, 28(8):42-45.