引入负荷温度梯度的负荷预测方法研究
程 卓
(深圳供电局有限公司,广东 深圳 518000)
负荷预测是电网规划的基础,其对电网规模的发展具有重要的指导意义。研究表明气温对区域负荷有很大的影响[1-9],随着温室效应增强以及厄尔尼诺现象频发,研究基于温度变化的负荷预测方法对电网发展有着越来越明显的意义。
负荷预测中考虑温度的影响相较于实测值的优势在于,实测最大负荷值与天气情况相关,极端天气易引起负荷短时内的升高,但不能反应真实的基础电力需求。以实测值直接外推,可能造成预测负荷偏差。
国内有很多论文研究了温度对区域电网的负荷特性的影响,部分文献指出其对负荷预测有重要指导意义,文献[10-15]研究了基于温度影响的负荷预测方法,但都是用于指导调度部门制订运行方式的短期负荷预测方法,较少有文献研究基于温度影响的中长期负荷预测方法。文献[16]将负荷分解为趋势性负荷和非趋势性负荷两部分,分别进行建模预测,其不足是文献基于两年数据对下一年负荷进行预测,忽略了随着时间的变化,其趋势性负荷的影响因子的比例系数也是变化的。
法国电力在负荷预测中也用到了温度校正,其做法是将历史负荷值进行温度校正,还原成基准温度下的负荷值,进而预测规划年基准温度下的负荷值,再将其折算到当年温度极值。
本文分析了大量的历史数据,通过分析近几年日最高温度与日最大负荷的相关关系,寻找到负荷的温度不敏感量与敏感量的变化规律。发现温度敏感负荷与温度之间的关联参数,称其为负荷温度梯度,其值逐年变化,并不能用近几年的数据得到的负荷温度梯度直接用到预测年,而是需要通过对负荷温度梯度进行预测,进而得到负荷预测值。
1 预测思路
引入负荷温度梯度的负荷预测方法简单来讲是将温度敏感负荷与温度不敏感负荷分离,用负荷温度梯度来表达温度敏感负荷与温度的变化规律,并用多年历史数据对预测年的负荷温度梯度进行预测,进而得到温度敏感负荷的预测值。同时对温度不敏感负荷进行预测。最终叠加得到负荷的预测值。
2 预测方法与步骤
2.1 寻找负荷与温度的关系
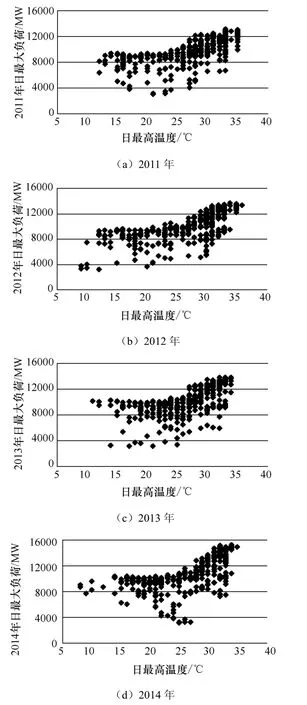
图1 日最高负荷与日最高温度散点图
以某市电网为例,将2011—2014年日最高负荷与日最高温度数据做散点图(图1所示),可以看出数据存在很强的规律性。在25℃以下,日最高负荷分布较大概率的集中在某值(标记此值为P0)附近,P0不随温度变化,即负荷的温度不敏感量;在25℃以上,日最高负荷随着温度的上升有明显的正相关关系,负荷中会有温度敏感量叠加,负荷的温度敏感的部分记为Pt,总负荷为P=Pt+P0。
2.2 确定负荷温度梯度变化规律
1)基础数据处理
设定温度基准值为25℃。对25℃以上的负荷与温度数据进行分析。考虑到负荷预测的目的是:预测负荷发展可能的最大值,来指导电网建设规模。只有负荷的最大值对负荷预测才是有意义的。因此剔除掉节假日、周末等日最高负荷明显相对较小的数据,减小其对负荷温度梯度参数的影响。
2)回归分析理论
本文通过最小二乘法做线性回归,其理论已经相当成熟,这里只作简单说明:对于y=ax+b的直线,其经验拟合方程参数如下:

其相关系数如下:

3)线性回归结果分析
以温度基准差(日最高温度减去基准温度)为自变量,日最大负荷为因变量,得到图2所示散点图。
由图2可以看出日最高温度与温度基准差呈线性关系。通过回归分析得到如下关系。
负荷的参数表达式如下:

式中,a为负荷温度梯度,a×(t-25) 为温度敏感负荷,P0为温度不敏感负荷。
2011—2014年的拟合关系如下:


图2 日最高负荷与温度基准差散点图
根据2011年至2014年的数据可以看出,随着经济的发展,人民生活水平的提高,负荷温度梯度和温度不敏感负荷都逐年增加。负荷温度梯度逐年增加反映出温度敏感负荷的总量逐年增加,温度每增加一度,会有更多的负荷上升。温度不敏感负荷反映出随着经济增长,工商业用电总量在增加。
2.3 对温度敏感负荷与温度不敏感负荷分别预测
对于温度敏感负荷:由上述分析可知,其与温度的关系为

可对负荷温度梯度a和温度t分别进行预测得到Pt的预测值。负荷温度梯度a的历史值见表1。

表1 2011—2014年负荷温度梯度
负荷温度梯度历史值逐年变大,十分接近一次函数。将其设为因变量,年份为自变量,利用最小二乘法,得到其关系如图3所示。
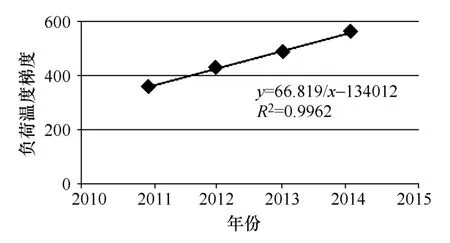
图3 负荷温度梯度与年份线性回归关系图
由此外推得到 2015年负荷温度梯度预测值为628.01。
根据历史年最大负荷日温度数据及该市气温情况,其最大负荷日最有可能出现的气温为34℃~35℃。其对应的2015年的温度敏感负荷预测值分别为

对于温度不敏感负荷:由上述分析,其值每年不随温度变化,且逐年增加。考虑到其反映了随着经济变化,工商业等基础用电需求的变化,可参考负荷总量的各种预测方法对其进行预测。这里简单的用趋势外推法来做说明。2011—2014年温度不敏感负荷值见表2。

表2 2011—2014年温度不敏感负荷
将其设为因变量,年份为自变量,利用最小二乘法,得到其关系如图4所示。
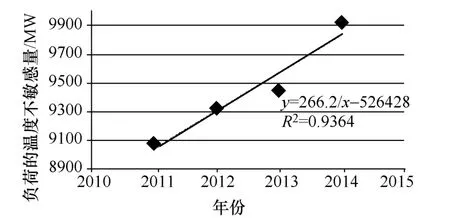
图4 温度不敏感负荷与年份线性回归关系图
外推得到 2015年温度不敏感负荷预测值为10106MW。
将 2015年温度敏感负荷预测值与温度不敏感负荷预测值叠加得到2015年负荷值预测结果见表3。

表3 不同温度下2015年负荷预测值
2.4 结果校核
与传统整体预测所得到的负荷预测结果进行对比。同样采用趋势外推法对负荷总量直接进行预测。
2011年至2014年年最大负荷值见表4。

表4 2011—2014年最大负荷
将其设为因变量,年份为自变量,利用最小二乘法,得到其关系如图5所示。

图5 年最大负荷与年份线性回归关系图
由此外推得到2015年负荷预测值为15614MW。另外该市电网“十三五”规划中2015负荷预测基础方案为15550MW,校核方案为16050MW。可以初步断定上述方法所得结果是合理的。
引入负荷温度梯度的预测方法通过对大量数据的分析得出温度敏感负荷与温度不敏感负荷的规律,对这两部分分别进行预测,对于温度敏感负荷,最小二乘法很好的拟合了负荷温度梯度的趋势,相关系数达到了 0.9962,而且对于极端温度能够做到较好的预估;对于温度不敏感负荷,其变化趋势与负荷总量有些类似,受经济的影响较大,可类比采用传统的对负荷总量进行预测的方法,而且由于剔除了温度的影响,从物理意义上讲对该部分的预测会更契合实际。因此相较于用实测值直接预测,实测最大负荷值与天气情况相关,极端天气易引起负荷短时内的升高,但不能反应真实的基础电力需求。以实测值直接外推,可能造成预测负荷偏差。
3 结论
本文研究了 2011—2014年日最高负荷与日最高温度数据之间的规律,将负荷分为了温度敏感负荷与不敏感负荷。通过对温度敏感负荷分析,发现逐年的负荷温度梯度的线性相关性很强,将负荷温度梯度这个参数引入到负荷预测中,分别对温度敏感负荷与不敏感负荷预测,从物理意义上将可以更好的作出预测,指导电网建设。
同时本文也存在一些不足,随着温度的升高,负荷的温度敏感部分会饱和,饱和值对电网发展有重要意义,值得进一步对此作出研究。
[1] 马瑞, 周谢, 彭舟, 等. 考虑气温因素的负荷特性统计指标关联特征数据挖掘[J]. 中国电机工程学报,2015, 35(1): 43-51.
[2] 朱振伟. 气象因素对电网负荷特性影响的研究[D].杭州: 浙江大学, 2008.
[3] 周谢. 电力负荷特性指标及其内在关联性分析[D].长沙: 长沙理工大学, 2013.
[4] 雷鸣, 朱昊, 高山. 温度变化对小区居民负荷特性的影响[C]. 电力系统及其自动化专业第二十一届学术年会论文集, 2005: 1487-1490.
[5] 陆建宇, 王亮, 王强, 等. 华东电网气象负荷特性分析[J]. 华东电力, 2006, 34(11): 38-42.
[6] 王颖. 温度对天津电网负荷的影响[J]. 天津电力,2006, 1: 7-9.
[7] 张海东, 孙照渤, 郑艳, 等. 温度变化对南京城市电力负荷的影响[J]. 大气科学学报, 2009, 32(4):536-542.
[8] 陈健, 刘明波, 樊亚亮, 等. 广州电网负荷特性分析[J]. 电力系统及其自动化学报, 2009, 21(6): 78-83.
[9] 於冬雪, 李扬, 周毅波. 南宁地区负荷特性及温度相关性分析[J]. 电力需求侧管理, 2013(5): 6-10.
[10] 原媛. 电力负荷特性分析及中长期负荷预测方法研究[D]. 上海: 上海交通大学, 2008.
[11] 谢家安. 基于体感温度的电力系统负荷分类及负荷预测[J]. 电网与清洁能源, 2012, 28(8): 24-28.
[12] 朱陶业, 李应求, 张颖, 等. 提高时间序列气象适应性的短期电力负荷预测算法[J]. 中国电机工程学报,2006, 26(23): 14-19.
[13] De Felice M, Alessandri A, Ruti PM. Electricity demand forecasting over Italy: Potential benefits using numerical weather prediction models[J]. Electric Power Systems Research, 2013, 104: 71-79.
[14] Dotzauer E. Simple model for prediction of loads in district-heating systems[J]. Applied Energy, 2002,73(3/4): 277-284.
[15] Roldán-Blay C, Escrivá-Escrivá G, Álvarez-Bel C, et al. Upgrade of an artificial neural network prediction method for electrical consumption forecasting using an hourly temperature curve model[J]. Energy and Buildings, 2013, 60: 38-46.
[16] 张凯锋, 藤贤亮, 王颖. 基于趋势分解的电力系统区域负荷建模与预测方法[C]. Proeeedings of the 31st Chinese ControI Conlference, Hefei, China, 2012.

