一种快速求核算法

周世睿,郭星

（安徽大学计算机科学技术学院，安徽，合肥 230000）

一种快速求核算法

周世睿,郭星

（安徽大学计算机科学技术学院，安徽，合肥 230000）

随着粗糙集理论在诸多领域的广泛应用，特别是针对海量数据应用粗糙集理论，对于实时性有了更高要求，在这种情况下针对求核与属性约简也提出了更高的要求，目前有许多粗糙集求核算法，但是在时间复杂度或者空间复杂度上都或多或少有着缺陷.本研究利用基数排序和二分法的思想设计了一种快速求核算法，其时间复杂度为O（|U||C|2）通过实验，证明了算法的正确性和高效性.

粗糙集；基数排序；二分法；核

1 引言

Rough粗糙集理论是波兰数学家Pawlak［1］在1982年提出的，是一种描述模糊与处理不确定数学问题的数学工具，由于无需先验知识，并且可以从规模巨大的数据中挖掘出隐含的信息，被广泛应用于人工智能、模式识别、数据挖掘等领域.启发式属性约简算法由于时间复杂度低，速度较快，因而应用较为广泛.求核作为常见启发式算法的重要步骤，重要程度不言而喻.

Skowron在1995年最早提出了基于差别矩阵的求核算法，Hu［2,3］等人对此算法加以改进.叶东毅［4］利用实例证明了Hu算法在对不一致决策表求核中存在错误，在改进差别矩阵的基础上，给出了一个新的差别矩阵的定义和求核方法；赵军［5］等基于决策系统的一致性，提出了一种不需要建立差别矩阵的核属性计算方法，但是该方法在处理不相容策表时，具有很大的局限性，为了解决因决策表的不相容性导致所求得的核出现错误的问题，闫德勤等将决策表规范化后再构造差别矩阵，然后利用规范化后建立的差别矩阵求核属性，其时间复杂度为O（|U||C|2）；杨明［7］提出了一种改进的差别矩阵及其求核方法.徐章艳［8］等给出了简化的差别矩阵的定义，并设计了一种求核算法，算法的时间复杂度被降为max（O（|U/C|2|C|）,O（|U||C|）但以上方法均需要创建差别矩阵或者简化的差别矩阵,如果样本的对象集很大，差别矩阵就要占用很多的空间，增加了计算量和计算时间，影响了计算效率［11,12］在本论文中的将介绍一种快速求核算法，该算法可以对不一致粗糙集求核，避免HU算法在不一致粗糙集求核中存在的问题，并且有较好的时间复杂度.本算法首先对不一致粗糙集进行预处理，通过修改不一致决策表内决策属性属性值，将不一致决策表转化为一致性决策表，并证明该一致性决策表的核属性等同于不一致决策表核属性.然后进行求核.并通过UCI数据集的实验证明本文的求核算法有较好的时间、空间复杂度.

2 基本定义

定义1［1］称五元组S=（U,A∪d,V,f）为信息系统，其中U为所有对象形成的非空有限集合，称为论域；A为属性的有限集合，d为决策属性.

定义2［2］若P⊆U，且P不等于空集，则P中所有等价关系的交集也是一个等价关系，称为P上的不可分辨关系，记为IND（P），且有IND（P）=∩［X］R.表示与等价关系族P相关的知识，称为K中关于U的P的基本知识即P的基本集.为简单起见，我们用U/P代替U/IND（P），IND（P）的等价类称为知识的基本概念或基本范畴.

定义3［2］在决策表S中，若对任意Xi∈U/C,存在Yj∈U/D,使得Xi∈Yj，则S为一致决策表.

定义4［4］叶东毅教授差别矩阵Mij中元素mij定义如下：

定义5［9］在决策表S=（U,A∪d,V,f）中，若POSc（D）=POS （c-｛a｝）（D）,且a∈C，则a称为C中相对D不必要的.若POSc （D）≠POS（c-｛a｝）（D），则a称为C中相对D必要的.Core（C）是C中所有必要属性集合，称为C的核集.

定义6［10］指出决策表核为差别矩阵中所有单个元素属性的合集，其求核公式为：

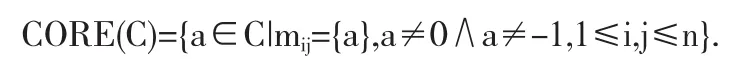
定义7［4］不可分辨关系，在决策表S=（U,A∪d,V,f）中，定义如下：

定义8新的决策表定义方式：S'=（U',C∪D',V',f'）其中D'=D'∪｛*｝，f'为信息函数满足∀x∈UC，有如下定义：

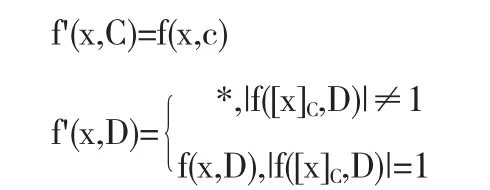
显然，新决策表S'是一个相容决策表.

定义9决策表分解对于决策表S=（U,C∪D,V,f）分解为两个子表：S1=（U1,C1'∪D,V,f）与子表S2=（U2,C2'∪D,V,f），其中：

3 等价性证明

3.1 证明原决策表S与转化后的一致性决策表S'核集具有等价性

叶东毅定义的差别矩阵，求核算法，改进了Hu算法不能处理不一致性决策表的问题，但时间空间性能较差.设Mij为原决策表S根据定义4转化的差别矩阵，Mij'∉｛mij'｝为S'根据定义8转化的差别矩阵，当∀mij∈M（mij≠ø），∃ma,b'=mij且mij'∉M'.

证明因为mij不为空，根据定理1可知：

反之，证明必要性.类似可证.

3.2 证明：决策表S的核集CORE（C）与子表S1、S2核集CORE（C1）CORE（C2）具有等价性，即CORE（C）=CORE（C1）∪CORE（C2）；该证明可以从两个方面进行，证明其充分性、必要性；充分性：若∀（ci∈C）∧（ci∈CORE（C）则必存在ci∈CORE （C1）∪CORE（C2）

证明根据定义6，核属性是差别矩阵中所有单个元素属性的集合，决策表S的差别矩阵记作Mij=｛mij｝，则一定有mij=ci，当ci∈C1时，由于mij=ci,即对象xi、xj在非ci的所有属性上取值相同，即只有ci能唯一分辨xi、xj两个对象.所以｛xi, xj｝⊆［xi］C2,|［xi］C2|≠1,所以根据定义9，xi、xj都属于U1，所以ci∈CORE（C1），同理当ci∈C2时，有ci∈CORE（C1）；综上充分性得证.

必要性：若∀ci∈CORE（C1）∪CORE（C2）且ci∈C则必存在：（ci∈C）∧（ci∈CORE（C））

证明因为ci∈CORE（C1）∪CORE（C2）且ci∈C，当ci∈CORE（C1）时，根据定义6，核属性是差别矩阵中所有单个元素属性的集合，决策表的S1差别矩阵记作M1ij=｛mij｝，则一定有mij=ci，由于mij=ci,即对象xi、xj在非ci的所有属性上取值相同，即只有ci能唯一分辨xi、xj两个对象.此时f（xi,t1）=f（xj,t1）.根据定义5，可知U/t1=U/C2；所以f（xi,C2）=f（xj,C2）,综上此时ci∈CORE（C1）.当ci∈CORE（C2）时，类似可证，综上，必要性得证.

实例分析：

Step1对于等价类，取代表元素，去除冗余对象：

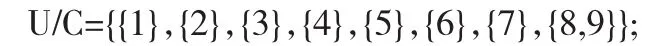
去除第九个对象；

添加两个新属性t1、t2，令U/t1=U/C2、U/t2=U/C1根据定义4：

产生两个子表S1、S2

S1

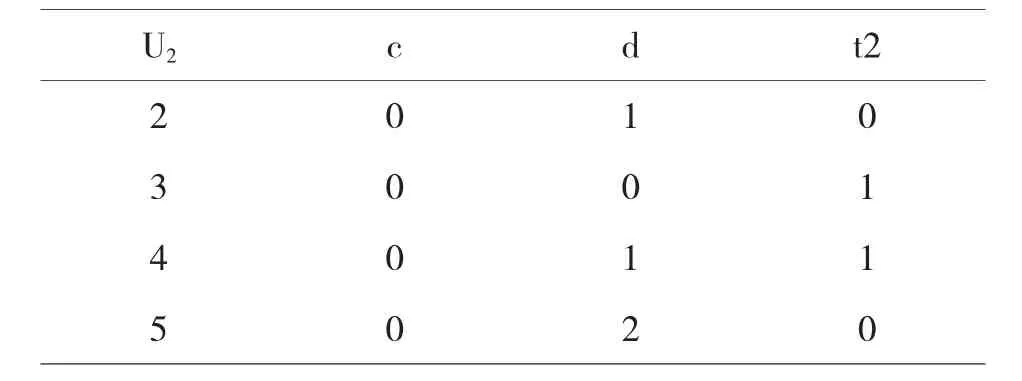
S2

4 算法具体步骤及性能比较分析

输入：一个决策表S=（U,C∪D,V,f）,其中U为对象集合，C为条件属性集合，D为决策属性集合.

输出：决策表S的核集CORE（C）

Step1：利用基数排序思想,对U按C生成等价类｛［x1］C，［x2］C，［x2］C，…［xn］C｝，然后利用定义2，修改决策属性，将不一致决策表转化为一致决策表.

Step2：删除一致性决策表中冗余信息.

Step3：读取决策表S内元素个数，记作n.

Step3：分别计算U按C1,C2生成的等价类，其中

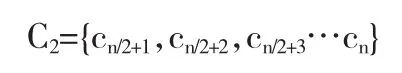
C1=｛c1，c2，c3…cn/2｝，通过等价类计算结果，按照定义5构造决策表S1，S2.

Step4：分别计算S1，S2的核集，按照定义5得出核集：

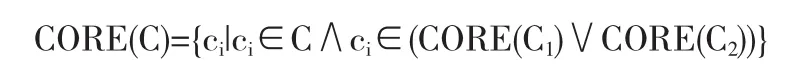
时间复杂度分析：step1，采用基数排序思想，划分等价类时间复杂度为：0（U*C）.

Step2,在每一个等价类中提取一个代表元素，其时间复杂度为：0（C）.

Step3时间复杂度为0（U*C）

实验本文选取了UCI数据库中中5组数据，分别用叶东毅教授求核方法与本文求核方法进行实验比较，实验环境为2.60GHz,2G内存，Window XP操作系统，算法开发在VS2010下进行，实验结果如下表所示：

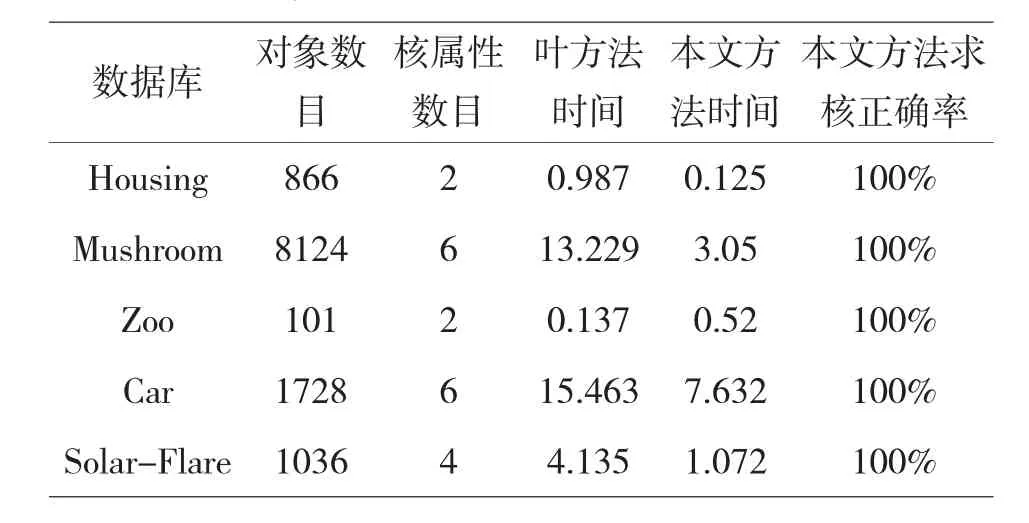
数据库对象数目核属性数目叶方法时间本文方法时间本文方法求核正确率Housing86620.9870.125100% Mushroom8124613.2293.05100% Zoo10120.1370.52100% Car1728615.4637.632100% Solar-Flare103644.1351.072100%

5.结论

本文将基数排序与二分法结合，提出了一种新的求核算法，并通过例子证明了该算法的正确性.本算法时间复杂度为O（|C||U|2）.由于本算法不需求取差别矩阵，空间复杂度与时间复杂度都较优.

〔1〕Pawlak Z.rough sets［J］.International of computer and information I science，1982，11（5）：341-356.

〔2〕Hu X，Cercone N.Learning in relational databases：.rough set approach［J］Computational intelligence，1995，11（2）：323-338.

〔3〕Skowron A，Rauszer C.The discernibility matrices and functions in information systems［M］/Intelligent Decision Support.Springer Nether lands，1992：331-362.

〔4〕叶东毅，陈昭炯.一个新的差别矩阵及其求核方法［J］.电子学报，2002，30（7）：1086-1088.

〔5〕赵军，土国撤，吴中福，等.一种高效的属性核计算方法［J］.小型微型计算机系统，2003，24（11）：1950-1953.

〔6〕闫德勤，刘菲斐.属性约简中的差别矩阵与近似精度［J］.小型微型计算机系统，2005，26（11）：1975-1977.

〔7〕杨明.一种基J飞改进差别矩阵的属性约简增量式更新算法［J］.计算机学报，2007，30（5）：815-822.

〔8〕徐章艳，杨炳儒，宋威.一个基于差别矩阵的快速求核算法［J］.计算机工程与应用，2006，42（6）：4-6.

〔9〕葛浩，李龙澎，杨传健.向向数据删除的核属性更新算法［J］.控制与决策，2012，27（5）.

〔10〕蒋瑜，王嘉响.一种快速属性核求解算法「J］.计算机工程与应用，2011，47（26）：53-54.

〔11〕钱文彬，杨炳儒，徐章艳，等.一种高效的核属性动态更新算法［J］.计算机科学，2012，39（7）：210-214.

〔12〕胡秦斌.一种基于决策信息系统的求核属性算法［J］.微电子学与计算机，2012，29（007）：23-25.

〔13〕张文修，吴伟志，梁吉业，等.粗糙集理论和方法［M］.北京：科学出版社，2001.

TP181

A

1673-260X（2015）05-0006-03