污水深度处理中超滤工艺对有机物的截留模型

黄韵清，孙 傅，曾思育，董 欣，陈吉宁

（清华大学环境学院，北京 100084）

污水深度处理中超滤工艺对有机物的截留模型

黄韵清，孙 傅，曾思育*，董 欣，陈吉宁

（清华大学环境学院，北京 100084）

基于浓差极化现象和膜孔堵塞效应，建立了污水深度处理中超滤工艺对有机物的截留模型.利用中试试验数据率定模型参数并验证模型的模拟效果.模型验证结果表明，该模型能够较好地模拟超滤工艺出水UV254值随时间的变化特征，基于最优参数得到的模拟值与相应实测值相对误差的绝对值均低于10%.并且模型参数区域灵敏度分析和不确定性分析结果表明，该模型的结构具有较高的可靠性.应用该模型研究了过滤时间、通量和进水浓度变化对出水水质的影响.结果表明，在过滤初期膜孔堵塞效应占主导地位并增加超滤膜对有机物的截留效果，在过滤后期浓差极化现象占主导地位并降低超滤膜对有机物的截留效果；当进水UV254浓度恒为0.1cm-1时，通量从5×10-5m/s增至1×10-4m/s，导致UV254截留率降低13%；当通量恒为5×10-5m/s时，进水UV254浓度从0.2cm-1降至0.1cm-1，使得出水浓度降低50%.因此，模型可应用于模拟进水水质和操作条件对污水深度处理中超滤工艺出水水质的影响，为从预处理、过滤周期和通量等方面改进和优化超滤工艺提供基础.

污水深度处理；超滤；截留；有机物；模型

超滤是一种能对溶液进行高效分离、净化、浓缩的低压膜分离技术，具有出水水质好、操作压力低、运行能耗低、占地面积小的特点，已在水处理等领域得到日益广泛的应用［1-4］.超滤对溶质的主要截留机理是筛除作用，这一过程受溶质性质、膜材料性质、溶液环境和操作条件等因素的影响［5］.此外，膜污染通过改变溶质与膜的相互作用，也会显著影响超滤对溶质的截留效果［6］.

为了更好地认识超滤工艺过程，从而有效地调控和优化工艺运行，从20世纪30年代开始很多学者对超滤工艺开展模拟研究［7-9］.目前，针对超滤工艺的模拟研究主要关注工艺过程中通量的变化［10-12］，针对水质变化的模拟研究较少，并且主要集中在食品、化工等领域［13-15］，水处理领域的相关研究更少.现有的超滤工艺水质模型既包括基于浓差极化（Concentration Polarization）［16-17］、阻碍传输（Hindered Transport）［13，18］、膜孔堵塞（Pore Blocking）［6，19］等理论的机理模型，也包括基于多元回归分析［14，20］、人工神经网络［15，21］等方法的经验模型.但是，针对食品、化工等行业建立的超滤工艺水质模型主要适用于单一溶质体系，无法直接应用于污染物成分复杂［22］的水处理过程.

建立数学模型，模拟污水深度处理中超滤对主要污染物指标的截留效果，并定量分析其影响因素，可以为工艺调控和优化运行提供决策支持.本文基于浓差极化理论和膜孔堵塞效应，建立了污水深度处理中超滤对有机物的截留模型，以中试试验数据对模型进行率定和验证，并研究了过滤时间、通量和进水浓度变化对出水水质的影响.

1 研究方法

1.1 模型概化

本文认为超滤对有机物的截留是浓差极化现象和膜孔堵塞效应共同作用的结果，并且二者对有机物截留效果产生相反的影响.浓差极化是指，在超滤过程中，溶质在膜表面不断积累，形成一层浓度高于主体溶液浓度的边界层，在边界层内溶质在浓度梯度的推动作用下向主体溶液扩散［23］.浓差极化现象越严重，超滤膜表面溶质浓度越高，透过液中溶质的浓度也越高，则超滤对溶质的截留率越低［23］.同时，在超滤过程中，污染物吸附在膜孔内和完全堵塞膜孔会导致超滤膜的膜孔缩小和有效传输面积减少，从而提高膜对溶质的截留效果［19，24］.在建模过程中，本文并未采用经典的Hermia模型［25］来描述膜污染.原因在于，Hermia模型的4种表达形式与溶质和膜孔径的相对大小密切相关，而污水厂二级出水中污染物成分复杂且尺寸差异较大，难以用任何一种Hermia模型表征超滤过程.因此，本文采用更为综合的模型方程来表征污染物吸附在膜孔内和完全堵塞膜孔导致的有效传输面积减少.

以恒通量过滤条件下的超滤工艺为研究对象，假设膜孔为一组垂直于膜表面的圆柱形细管，流过孔径的水流为层流，并且膜表面不形成较厚的滤饼层或凝胶层.在超滤过程中，由于污染物的吸附和堵塞，膜的有效传输面积随时间增加而逐渐减少，结合王旭东等［26］对膜结构参数的分析，设定t时刻膜的有效传输面积可表示为：

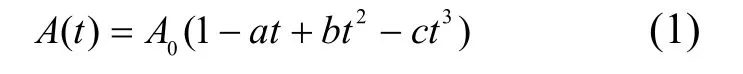
式中：A0和A（t）分别表示初始时刻和t时刻膜的有效传输面积（m2），t表示时间（s），a、b和c为模型参数.根据膜孔径、膜孔密度和膜面积，可计算得到初始时刻膜的有效传输面积A0.

当流过孔径的水流是层流时，可认为溶质通过膜孔的传输是由分子扩散造成的［19］，则透过膜的溶质通量可以表示为：

式中：NA表示跨膜溶质通量，kg/（m2·s）；D表示溶质扩散系数，m2/s；l表示膜厚，m；cm和cp分别表示膜表面和出水中的溶质浓度，kg/m3.

跨膜非稳态质量守恒可表示为［19］：

式中：V表示出水体积，m3；Q表示流量，m3/s.

浓差极化层内的质量守恒可表示为：

式中：J表示出水通量，m/s；K表示传质系数，m/s；cb表示进水溶质浓度，kg/m3.

根据式（1）～式（4），可得：

考虑于污水厂二级出水中污染物成分复杂且尺寸差异较大，难以用常规公式分别确定扩散系数D和传质系数K的取值，故设定一个综合参数f=DeJ/K，则式（5）可转化为：

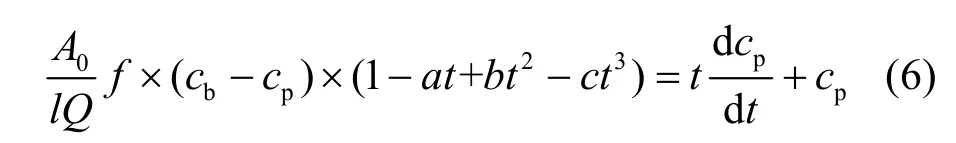
式（6）为污水深度处理中超滤对有机物的截留模型，能够预测出水中有机物浓度随过滤时间的变化.模型包括a、b、c和f共4个参数.其中，a、b和c 反映了超滤过程中膜孔堵塞的速率，f则能够综合反映溶质性质、水力学条件和操作条件等影响.该方程可在Matlab软件中利用分离变量法求解.

1.2 参数率定

本文中超滤模型率定和验证的数据来自中试试验［27］.该试验以稀释后的造纸黑液为原水，超滤膜选用聚砜中空纤维膜，膜截留分子量为100kDa.过滤方式为恒通量过滤，过滤周期为60min.该试验选择UV254值作为有机物含量的评价指标，并且进水UV254值平均为0.130cm-1，与污水处理厂二级出水的UV254值相当［28］.

由于式（6）中模型参数综合体现多种因素的共同影响，不便于直接测定，因此采用Hornberger-Spear-Young（HSY）算法率定模型参数.HSY算法率定模型参数得到的是模型参数的分布，而非单一的最优参数值，从而在一定程度上避免“最优”参数失真带来的决策风险［29-30］.其主要步骤包括［31］：

（1） 确定参数的取值空间和概率分布；

（2） 根据已有监测数据和模拟要求，确定模拟结果优劣的判断准则，将模拟结果分为可接受和不可接受2种类型；

（3） 在参数取值空间进行拉丁超立方采样（Latin Hypercube Sampling），利用采样得到的一组参数进行系统模拟；

（4） 根据（2）中确定的判断准则，将该组参数的模拟结果及参数归类，即对应于（2）中的2种类型；

（5） 重复（3）和（4），直至找到足够的可接受参数.

在此基础上，采用区域灵敏度分析（Regional Sensitivity Analysis， RSA）方法，分析模型参数的灵敏度.该方法考虑了模型结构复杂性引起的参数之间相关性的影响，而非仅靠变动单个参数的取值得到模型响应的变化［32］.对于每个模型参数，利用Kolmogorov-Smirnov（K-S）检验，判断可接受和不可接受两个参数样本是否服从相同的概率分布，如果二者的分布在统计意义上具有显著差异，则认为该参数是灵敏参数，否则就不是灵敏参数［33］.

1.3 模型验证

在模型参数率定结果的基础上，本文选择可接受的且在参数率定时使得模拟值与实测值相对误差绝对值之和最小的一组参数作为最优参数.利用最优参数进行模型验证，得到基于最优参数的模拟值.同时，本文还利用模型参数率定得到的所有可接受参数进行模型验证，得到基于所有可接受参数的模拟值.将基于最优参数和所有可接受参数的模拟值与相应的实测值进行对比，综合评价模型验证结果.

1.4 模型应用

本文利用模型参数率定得到的最优参数，模拟过滤时间、通量和进水浓度变化对超滤截留有机物效果的影响，从而为改进超滤工艺提供参考.

2 结果与讨论

2.1 参数率定

表1 参数初始取值范围和率定结果Table 1 Initial ranges for model calibration and optimal parameter values

根据文献［19，34-35］确定模型参数的初始取值范围，如表1所示，且认为每个参数均服从均匀分布.设定可接受模拟结果为模拟值与实测值的相对误差在±20%范围内.利用1个过滤周期内不同时刻超滤膜进出水UV254值的17组数据进行参数率定.采样得到40000组参数，其中1129组为可接受参数，使得模拟值与实测值相对误差绝对值之和最小的最优参数亦列在表1中.模型参数取最优值时，超滤出水UV254的模拟值与相应实测值的对比如图1所示.从图1中可看出，模拟值与实测值总体符合较好，88%数据点的相对误差在±10%范围内.

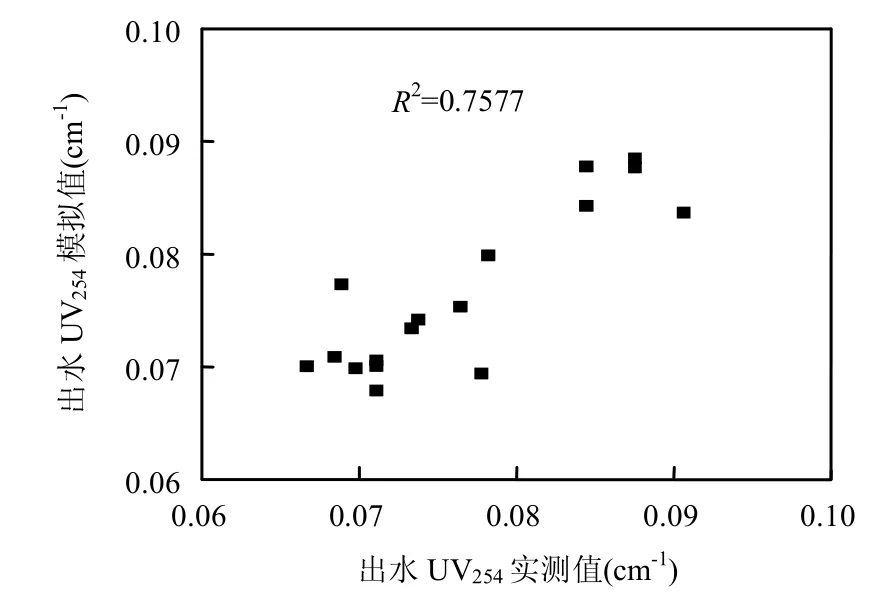
图1 超滤出水UV254模拟值与实测值的对比Fig.1 Comparison of simulated and observed UV254of the effluent of ultrafiltration

表2所示为可接受和不可接受参数的K-S检验统计量，相应的K-S检验临界值为0.041.从图2中可看出，4个参数的可接受和不可接受参数集合的累积分布曲线清晰分离，置信度为0.95的K-S检验结果也表明，可接受和不可接受参数集合的分布在统计意义上具有显著差异，因而4个参数均为灵敏参数.高比例的灵敏参数体现了模型结构的均衡性［33］.根据K-S检验统计量的大小，可确定4个参数灵敏度从高到低的排序为f＞b＞c＞a.从图2还可以看出，4个参数的概率密度均出现较为明显的峰值，因此可识别性较强，并且参数的不确定性有所下降.以标准偏差来衡量，a、b、c和f这4个参数的可接受参数集合的不确定性较初始取值范围分别下降了4%、33%、15%和50%.由此可见，4个参数灵敏度和不确定性下降比例由高到低的排序完全一致，说明在本文建立的模型中灵敏度越高的参数得到了越好的识别，这也预示着该模型的模拟结果具有较高的可靠性［33］.

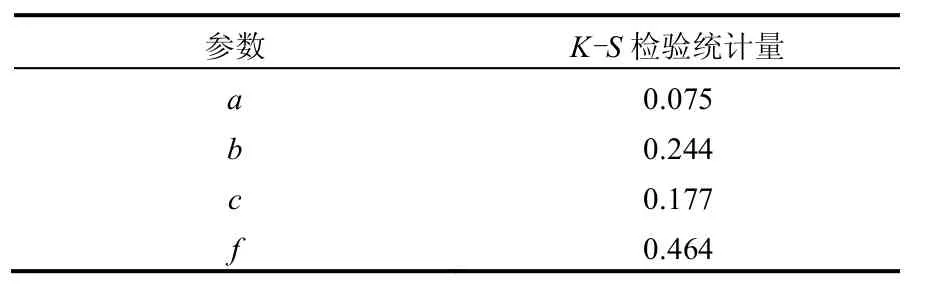
表2 可接受和不可接受参数的K-S检验统计量Table 2 K-S test statistics of behavior-giving and nonbehavior-giving parameters

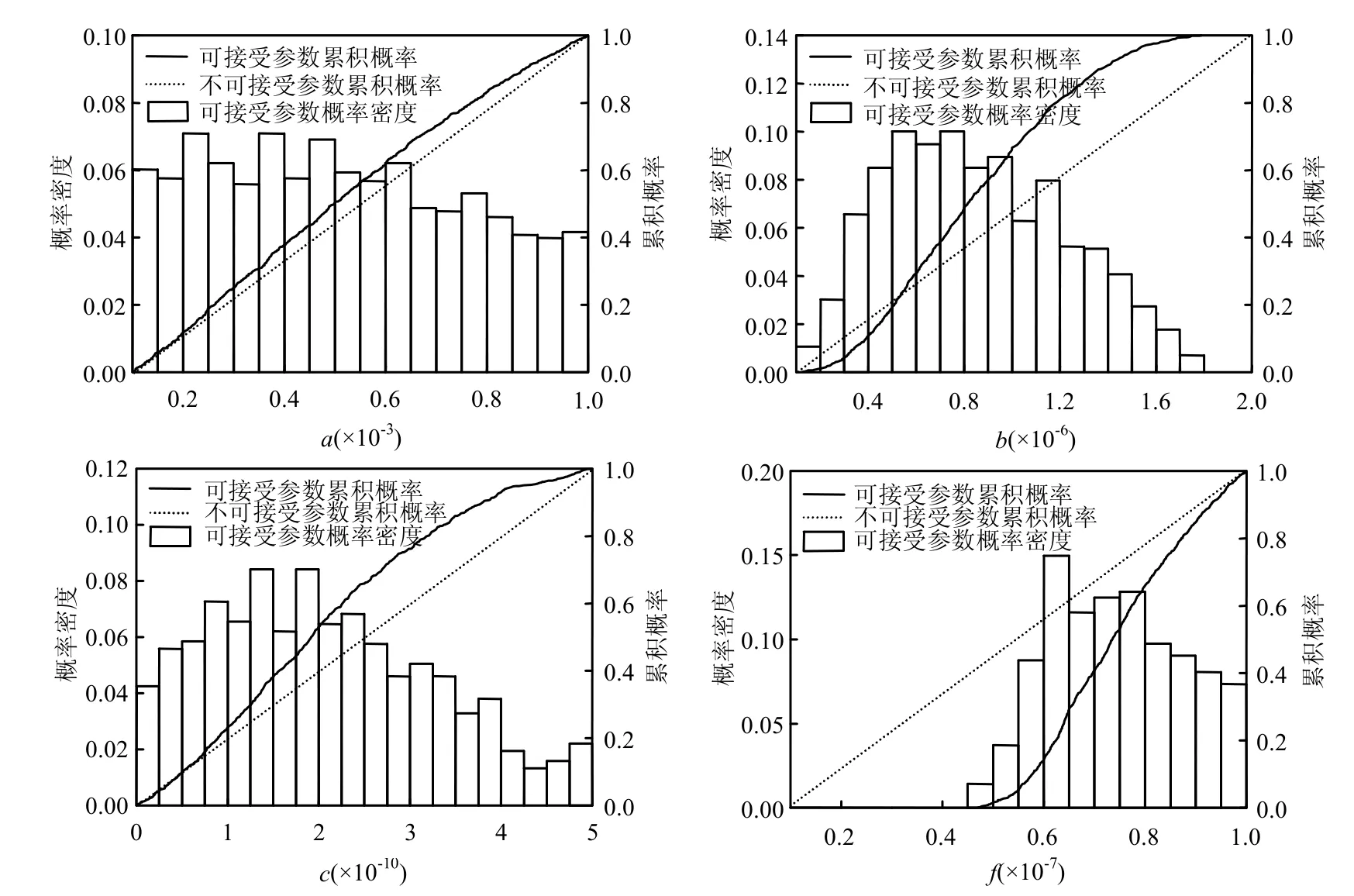
图2 模型参数的概率分布Fig.2 The probability distribution of model parameters

2.2 模型验证

采用超滤进出水UV254值的另外17组数据进行模型验证，结果如图3所示.从图3中可看出，基于最优参数得到的模拟值与相应实测值符合较好，并且较好地再现了出水UV254值随时间的变化趋势.个别数据点处模拟值与实测值偏差相对较大的原因，可能在于进水水质和操作条件的波动性.但总体来说，模型模拟效果较好，基于最优参数得到的模拟值与相应实测值相对误差的绝对值均低于10%.图3还同时给出了用1129组可接受参数进行模型验证的结果，即对每一个时刻可以得到1129组水质模拟结果.从图3可以看出，基于所有可接受参数的模拟值与实测值呈现相似的变化趋势，且实测值均落在相应时刻模拟值的分布范围内，进一步证明了模型的可靠性.

图3 超滤出水UV254模拟值与实测值的对比Fig.3 Comparison of simulated and observed UV254ofthe effluent of ultrafiltration

2.3 模型应用

利用本文建立的超滤模型和参数率定得到的最优参数，图4给出了在进水UV254值（cb）保持恒定的条件下，不同通量（J）时出水UV254值（cp）随时间的变化.从图4可以看出，随着过滤时间的增加，出水UV254值呈现先降低后升高的特征.主要原因是，过滤初期膜孔堵塞效应较为显著，从而增加了超滤膜对溶质的截留效果，这与Polyakov等［6］和Alventosa-deLara等［24］的研究结果一致.随着过滤时间的延长，浓差极化现象加剧，超滤膜表面溶质浓度增加，出水溶质的浓度也相应升高.从图4还可以看出，在通量越高的情况下，出水UV254值也越高.主要原因是，在高通量的情况下，浓差极化现象较为严重，从而降低了超滤膜对溶质的截留效果，这与Tsapiuk等［36］和Van Oers等［37］的研究结果一致.

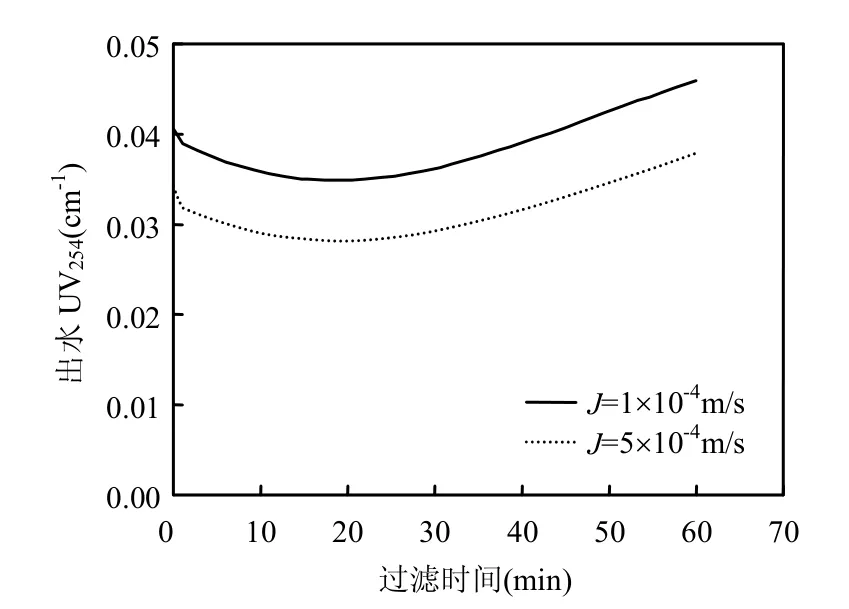
图4 不同通量下出水UV254值的时间变化（进水UV254值恒为0.1cm-1）Fig.4 Time variation of permeate UV254at different fluxes with constant feed concentration （0.1cm-1）

图5给出了通量（J）恒定时，不同进水浓度（cb）条件下出水UV254值（cp）随时间变化的模拟结果.从图5可以看出，进水浓度越高，出水浓度也越高，这与Alventosa-deLara等［24］的研究中观察到的现象一致.主要原因是，较高的进水浓度增加了溶质通过膜的可能性［24］，并且导致更多溶质在膜表面积累，加剧了浓差极化现象［38］，从而提高了出水浓度.

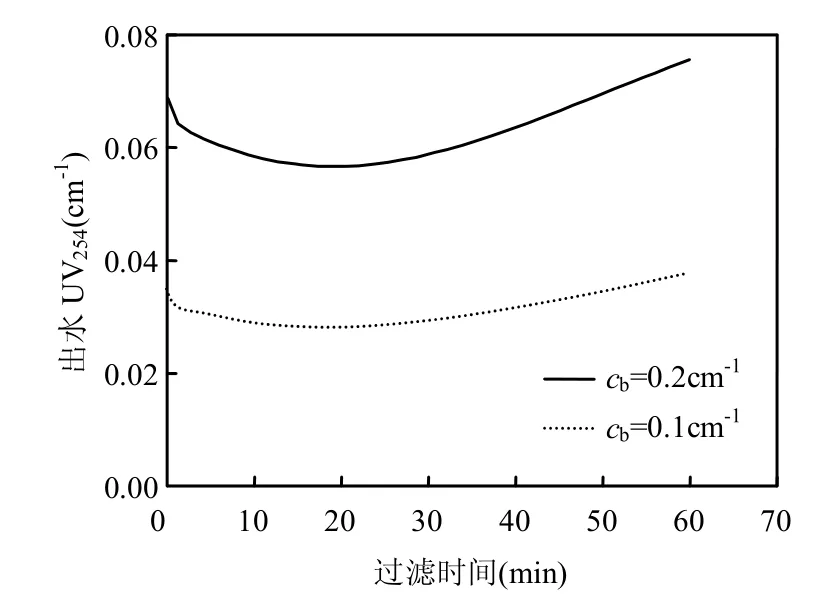
图5 不同进水浓度下出水UV254值的时间变化（通量恒为5×10-5m/s）Fig.5 Time variation of permeate UV254at different feed concentrations with a constant flux （5×10-5m/s）

2.4 讨论

本文开发的模型较好地模拟了污水深度处理中超滤工艺对有机物的截留效果，能够再现过滤时间、通量和进水浓度等影响因素作用下超滤出水中有机物浓度的动态变化特征，并且模型参数区域灵敏度分析和不确定性分析结果也表明该模型的结构具有较高的可靠性.

同时，本文建立的超滤工艺水质模型尚存在以下两方面局限.一方面，与现有的很多超滤工艺水质模型一样，本文的模型是基于中试试验数据而非现场数据建立的，这在一定程度上限制了模型应用于实际系统时的可靠性.当进水水质、膜材料性质和操作条件等因素变化时，模型的适用性有待进一步验证.另一方面，由于数据限制，本文在建立模型时对模型方程进行了较大程度的简化.这一做法的优点是简化了模型结构，增强了模型参数的可识别性（图2），使得模型简单易用；其缺点在于，4个参数实际上是多种影响因素的综合表达，因此难以分别确定各个因素对超滤过程的影响.未来可以在数据条件允许的情况下，进一步细化模型过程和机理的描述，从而完善模型.

建议利用实际污水深度处理系统的现场监测数据检验该模型的适用性，并根据需要进一步改进和完善模型机理，引入其他必要的水质指标和运行参数，更为深入细致地描述膜材料性质、进水水质特征、运行条件等因素对超滤工艺截留污染物效果的影响.

3 结论

3.1 提出了污水深度处理中超滤工艺对有机物的截留模型.该模型综合考虑了超滤过程中的浓差极化现象和膜孔堵塞效应.利用中试试验数据对模型进行参数率定和模型验证，结果表明该模型能够较好地模拟超滤工艺出水UV254值随时间的变化特征，并且模型结构具有较高的可靠性.

3.2 在过滤初期膜孔堵塞效应占主导地位并增加超滤膜对有机物的截留效果，在过滤后期浓差极化现象占主导地位并降低超滤膜对有机物的截留效果.模型也较好地模拟了通量和进水浓度等影响因素作用下超滤出水中有机物浓度的动态变化特征.因此，该模型可应用于模拟进水水质和操作条件对污水深度处理中超滤工艺出水水质的影响，评估从预处理、过滤周期和通量等方面改进和优化超滤工艺的可行性及效果.

［1］Chiu K， Gramith K， Oppenheimer J， et al. Development of a microfiltration and ultrafiltration knowledge base ［M］. Denver：American Water Works Association， 2005.

［2］石柳青.超滤在饮用水净化和城市污水深度处理中的应用研究［D］. 北京：清华大学， 2011.

［3］周海东，黄 霞，王晓琳，等.两种工艺对污水再生水中微量有机物的去除效果 ［J］. 中国环境科学， 2009，29（8）：816-821.

［4］刘茉娥，蔡邦肖，陈益棠.膜技术在污水治理及回用中的应用［M］. 北京：化学工业出版社， 2005.

［5］Acero J L， Benitez F J， Teva F， et al. Retention of emerging micropollutants from UP water and a municipal secondary effluent by ultrafiltration and nanofiltration ［J］. Chemical Engineering Journal， 2010，163（3）：264-272.

［6］Polyakov Y S， Zydney A L. Ultrafiltration membrane performance： Effects of pore blockage/constriction ［J］. Journal of Membrane Science， 2013，434：106-120.

［7］Chakraborty S， Dasgupta J， Farooq U， et al. Experimental analysis， modeling and optimization of chromium （VI） removal from aqueous solutions by polymer-enhanced ultrafiltration ［J］. Journal of Membrane Science， 2014，456：139-154.

［8］Palencia M， Rivas B L， Valle H. Size separation of silver nanoparticles by dead-end ultrafiltration： Description of fouling mechanism by pore blocking model ［J］. Journal of Membrane Science， 2014，455：7-14.

［9］Ferry J D. Statistical evaluation of sieve constants in ultrafiltration ［J］. The Journal of General Physiology， 1936，20（1）：95-104.

［10］Nguyen T， Yoshikawa S， Karasu K， et al. A simple combination model for filtrate flux in cross-flow ultrafiltration of protein suspension ［J］. Journal of Membrane Science， 2012，403：84-93.

［11］Vela M， Blanco S Á， García J L. Crossflow ultrafiltration of cake forming solutes： a non-steady state model ［J］. Desalination， 2005，184（1）：347-356.

［12］马 琳，秦国彤.膜污染的机理和数学模型研究进展 ［J］. 水处理技术， 2007，33（6）：1-4.

［13］Morão A， Nunes J C， Sousa F， et al. Development of a model for membrane filtration of long and flexible macromolecules：Application to predict dextran and linear DNA rejections in ultrafiltration ［J］. Journal of Membrane Science， 2009，336（1）：61-70.

［14］Lin S， Hung C， Juang R. Effect of operating parameters on the separation of proteins in aqueous solutions by dead-end ultrafiltration ［J］. Desalination， 2008，234（1）：116-125.

［15］Rai P， Majumdar G C， Dasgupta S， et al. Modeling the performance of batch ultrafiltration of synthetic fruit juice and mosambi juice using artificial neural network ［J］. Journal of Food Engineering， 2005，71（3）：273-281.

［16］Bhattacharjee C， Datta S. A numerical simulation for the prediction of flux and rejection during ultrafiltration in unstirred batch cell using variable diffusivity concept ［J］. Separation and Purification Technology， 2001，24（1）：13-22.

［17］Bhattacharjee C， Sarkar P， Datta S， et al. Parameter estimation and performance study during ultrafiltration of Kraft black liquor［J］. Separation and Purification Technology， 2006，51（3）：247-257.

［18］Morão A， Pessoa De Amorim M T， Lopes A， et al. Characterisation of ultrafiltration and nanofiltration membranes from rejections of neutral reference solutes using a model of asymmetric pores ［J］. Journal of Membrane Science， 2008，319（1）：64-75.

［19］Ghose S， Bhattacharjee C， Datta S. Simulation of unstirred batch ultrafiltration process based on a reversible pore-plugging model［J］. Journal of Membrane Science， 2000，169（1）：29-38.［20］Ruby-Figueroa R， Cassano A， Drioli E. Ultrafiltration of orange press liquor： Optimization of operating conditions for the recovery of antioxidant compounds by response surface methodology ［J］. Separation and Purification Technology， 2012， 98：255-261.

［21］Razavi M A， Mortazavi A， Mousavi M. Dynamic modelling of milk ultrafiltration by artificial neural network ［J］. Journal of Membrane Science， 2003，220（1）：47-58.

［22］孟晓荣，张海珍，王 磊，等.城市污水二级出水超滤膜污染与膜特性的研究 ［J］. 环境科学， 2013，34（5）：1822-1827.

［23］莫颖慧.污水纳滤深度处理的膜污染及其对微量有机物截留的影响 ［D］. 北京：清华大学， 2013.［24］Alventosa-Delara E， Barredo-Damas S， Alcaina-Miranda M I， et al. Ultrafiltration technology with a ceramic membrane for reactive dye removal： optimization of membrane performance ［J］. Journal of Hazardous Materials， 2012，209：492-500.

［25］Hermia J. Constant pressure blocking filtration laws-application to powder-law non-Newtonian fluids ［J］. Institution of Chemical Engineers Transactions， 1982，60（3）：183-187.

［26］王旭东，王 磊，段文松，等.污水深度超滤过程的数学模拟及应用研究 ［J］. 水处理技术， 2006，32（7）：20-22.

［27］郭小桐.操作条件及运行模式对超滤水处理过程的影响研究［D］. 西安：西安建筑科技大学， 2007.

［28］陈 颉.再生水的深度处理技术及回用的健康风险评价 ［D］.邯郸：河北工程大学， 2009.

［29］刘 毅，陈吉宁，杜鹏飞.环境模型参数识别与不确定性分析 ［J］.环境科学， 2002，23（6）：6-10.

［30］徐一剑，曾思育，张天柱.基于不确定性分析框架的动态环状河网水质模型 ［J］. 水科学进展， 2005，16（4）：574-580.

［31］邓义祥，陈吉宁.HSY 算法在水质模型参数识别中的应用探讨［J］. 上海环境科学， 2002，21（8）：497-500.

［32］孙 傅.给水系统水质风险模拟与管理策略研究 ［D］. 北京：清华大学， 2007.

［33］Sun F， Chen J， Tong Q， et al. Structure validation of an integrated waterworks model for trihalomethanes simulation by applying regional sensitivity analysis ［J］. Science of the Total Environment， 2010，408（8）：1992-2001.

［34］Karode S K. A new unsteady-state model for macromolecular ultrafiltration ［J］. Chemical Engineering Science， 2000，55（10）：1769-1773.

［35］段文松.城市污水深度处理过程中超滤膜结构参数模型的建立及应用分析研究 ［D］. 西安：西安建筑科技大学， 2005.

［36］Tsapiuk E A， Bryk M T， Kochkodan V M， et al. Separation of aqueous solutions of nonionic organic solutes by ultrafiltration ［J］. Journal of Membrane Science， 1990，48（1）：1-23.

［37］Van Oers C W， Vorstman M， Kerkhof P. Solute rejection in the presence of a deposited layer during ultrafiltration ［J］. Journal of Membrane Science， 1995，107（1）：173-192.

［38］Bhattacharjee C， Datta S. Analysis of mass transfer during ultrafiltration of PEG-6000in a continuous stirred cell： effect of back transport ［J］. Journal of Membrane Science， 1996，119（1）：39-46.

Modeling organics rejection during ultrafiltration in advanced wastewater treatment.

HUANG Yun-qing， SUN Fu，ZENG Si-yu*， DONG Xin， CHEN Ji-ning （School of Environment， Tsinghua University， Beijing 100084， China）.

China Environmental Science， 2015，35（2）：420～426

Based on the concentration polarization theory and pore blocking effect， a model was developed to predict organics rejection during ultrafiltration in advanced wastewater treatment. The model was calibrated and validated against data collected from pilot-scale experiments. Results of model validation indicated that the model could well predict the time variations of permeate UV254during ultrafiltration with absolute relative errors between simulated and observed data less than 10%. Regional sensitivity analysis and uncertainty analysis of model parameters suggested that the model exhibit a robust and reliable structure. The influence of different operating conditions， including filtration time， flux and feed concentration， on permeate concentration was investigated with the developed model. Results indicated that the pore blocking effect dominated in the initial stage of ultrafiltration and increased the rejection rate of organics， whereas concentration polarization effect dominated the rest and decreased rejection. The rejection rate of UV254， with a constant feed concentration of 0.1cm-1， was decreased by 13% when the flux increased from 5×10-5m/s to 1×10-4m/s. With a constant flux of 5×10-5m/s， however， the permeate UV254concentration was 50% lower at a feed concentration of 0.1cm-1than that at 0.2cm-1. Therefore the model could simulate the influences of influent quality and operating conditions on effluent quality for the ultrafiltration process in advanced wastewater treatment， and thus provide decision support for the optimization of ultrafiltration with respect to pretreatment， filtration period and flux.

advanced wastewater treatment；ultrafiltration；rejection；organics；model

X703.1

A

1000-6923（2015）02-0420-07

黄韵清（1990-），女，浙江温州人，清华大学硕士研究生，主要从事环境系统分析方法研究.

2014-05-19

水体污染控制与治理科技重大专项（2009ZX07318-008）

* 责任作者， 副教授， szeng@mail.tsinghua.edu.cn