垂直Bridgman法生长CaF2单晶传热过程的数值分析

姚 静，周 海，卢一民，万汉城

（1.北京化工大学材料科学与工程学院，北京 100029；2.北京石油化工学院材料科学与工程学院，北京 102617）

垂直Bridgman法生长CaF2单晶传热过程的数值分析

姚 静1，2，周 海2，卢一民2，万汉城2

（1.北京化工大学材料科学与工程学院，北京 100029；2.北京石油化工学院材料科学与工程学院，北京 102617）

采用有限元法对大尺寸氟化钙单晶的生长过程进行了传热分析，准稳态模型简化模拟计算过程.研究了梯度区不同的温度梯度对界面形状和晶体生长速度的影响，讨论了辐射传热对晶体生长过程传热的影响.研究表明：晶体生长过程中界面凸度发生变化；晶体生长速率与坩埚下降速率不一致；25 K/cm为合适的梯度区温度梯度；晶体内部辐射传热对单晶生长传热过程有重要影响.计算结果表明，3个时期的固相等温线的曲率小于液相的.根据数值模拟结果进行了晶体生长实验，生长出的晶体完整，透明，无宏观缺陷.

CaF2；有限元法；垂直Bridgman法；数值模拟；传热；温度场

氟化钙（CaF2）单晶是一种具有广泛应用前景的光学晶体材料，其大尺寸单晶的制备一直备受人们关注［1-3］.垂直布里奇曼法是生长大尺寸氟化钙单晶的重要方法之一.晶体生长过程中的热传递对固-液界面的形状和曲率具有极重要的影响［4-6］，尤其是大尺寸氟化钙单晶的生长，固-液界面的形状和曲率［7-8］对单晶质量具有决定性作用.热传递的数值模拟分析对固-液界面的形状和曲率具有较好的预测作用［7-8］，其模拟结果可为制定合适的晶体生长参数提供依据.

垂直布里奇曼法生长大尺寸氟化钙单晶的热传递过程是一个瞬态过程，生长模型由一系列与时间相关的偏微分方程组成.与时间相关的偏微分方程在求解过程中存在很大的难度，准稳态模型则可简化求解过程.晶体的生长速度十分缓慢（＜1 mm/h），因此，准稳态模型适用于垂直布里奇曼法生长大尺寸氟化钙单晶传热过程中.LU等［9］应用准稳态模型模拟计算垂直布里奇曼法生长直径为10 mm的氟化钙晶体的过程，分析了生长过程中温度分布和固-液界面形状等问题.目前，国内相关研究多限于半导体生长系统的模拟，氟化钙晶体固相热导率大于液相热导率，而半导体系统则与之相反，因此，大尺寸氟化钙单晶的传热过程与半导体系统存在较大差异.

本文将结合垂直布里奇曼法生长直径为200 mm的氟化钙单晶的传热过程，利用FLUENT数值软件，模拟计算氟化钙单晶生长的传热过程.将石墨坩埚、坩埚内部的物料和周围环境作为一个研究整体，并考虑热辐射、热传导和相变潜热对生长过程的传热影响.模拟包括15、20和25 K/cm 的3个不同温度梯度，并分析了这3个温度梯度对固-液界面的形状和曲率的影响.

1 生长系统和控制方程

1.1 垂直布里奇曼法生长系统

垂直布里奇曼法生长系统的简图如图1所示.图中，r表示沿坩埚径向的长度，z表示沿坩埚轴向的长度.坩埚具有轴对称性，应用简化的二维坐标系（r，z），坐标原点位于坩埚底部的中心，坩埚的壁厚为2 mm，坩埚锥角为90°［10］.垂直布里奇曼法生长系统包含高温区、梯度区和低温区3个温区［11］.高温区、梯度区和低温区均为一恒定的温度梯度，高温区的温度梯度＜低温区的温度梯度＜梯度区的温度梯度.晶体生长过程中，坩埚下降速度（v）为恒定的，v=1 mm/h.坩埚内的温度分布随时间的改变建立传热模型，应用准稳态模型求解传热过程.模拟过程中，氟化钙的物性参数如表1所示，忽略温度和波长对热物理性质的影响.

图1 垂直Bridgman法的晶体生长系统示意图

垂直布里奇曼法生长系统的几何特征如下：坩埚内经R为20 cm；坩埚壁厚d为0.2 cm；坩埚长度L为30 cm；高温区长度L为50 cm；低温区长度L为30 cm；温度梯度区长度L为5 cm；高温区温度梯度G为3 K/cm；低温区温度梯度G为5 K/cm；坩埚角度θ为90°；传热系数h1，h2，h3，h4分别为0.05，0.04，0.07，0.07 W/（cm2·K）.

计算的网格采用GAMBIT软件生成，计算的网格文件由2 875个四边形和三角形的混合元素构成，并优化界面附近的网格.

表1 氟化钙（CaF2）的物理性质［12-13］

1.2 控制方程

氟化钙的物性参数决定垂直Bridgman法生长其晶体的坩埚下降速度十分缓慢，坩埚的下降速度v=0.1 cm/h.对于本系统［14］，

式中：τgrowth、τconduction和τconvection分别为晶体生长的时间尺度、热传导的时间尺度和对流传热的时间尺度；D为坩埚内部最大深度；g为重力加速度；v为坩埚下降速度；α为熔体的热扩散系数；β为熔体的热膨胀系数；ΔT为熔体中的温差.式（1）计算表明，热传导的时间尺度快于晶体生长的时间尺度两个数量级，对流传热的时间尺度快于晶体生长的时间尺度6个数量级，因此，本系统的传热模拟过程适用于准稳态模型［15］.应用准稳态模型，对模型作如下假设：a）系统处于准稳态；b）模型具有轴对称性；c）熔体的自然对流传热被忽略.熔体，晶体和坩埚的能量方程为

式中：T为温度；ρm、ρs和ρc分别为熔体密度、晶体密度和坩埚密度；Cp，m、Cp，s和Cp，c分别为熔体热熔、晶体热熔和坩埚热熔；km、ks和kc分别为熔体热导率、晶体热导率和坩埚热导率；∇为梯度算子.

氟化钙（CaF2）属于半透明材料，应用扩散近似.修正的热导率（ki）［9，16-17］为

1.3 边界条件

边界条件的确定直接影响研究系统内的温度分布［18］.坩埚外表面的边界条件［9，13］为

式中：kc为石墨坩埚的热导率；hi为传热系数；TA为坩埚壁处的温度；Tf为相对环境的温度；ε为坩埚的发射率；σ为Stefen-Boltzmann常数.

界面处的边界条件为

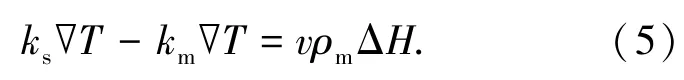
式中：v为拉伸速度；ΔH为结晶潜热.

在对称轴（r=0）处，温度分布呈轴对称分布，

坩埚上壁的温度为常量，坩埚下壁的温度为常量，坩埚侧壁的温度梯度：冷区为5 K/cm；梯度区分别为15、20和25 K/cm；热区为3 K/cm.

2 数值模拟结果分析

2.1 等温线分布和界面形状

有限元商业软件FLUENT求解方程（1）～（5），使用牛顿-拉夫逊迭代算法，能量方程的收敛标准为小于10-6，迭代160次后得到收敛的结果.为了表征固-液界面的弯曲程度，定义一个量度.凸度C定义为晶体中心轴与晶体边界处界面的纵坐标之差. C值为正，则表示界面凸向熔体，界面为凸界面；C值为负，则表示界面凹向熔体，界面为凹界面.

图2为在梯度区的温度梯度为20 K/cm下，不同生长时期的固-液界面位置和等温线分布.由图2可知，虚线表示结晶界面（T=1 653 K），晶体生长的3个不同时期，固相的等温线的曲率均小于液相的，这是由于固相的导热率远大于液相的导热率所导致［19］，如表1所示，固相热导率是液相热导率的10倍.C值均为正，说明晶体生长过程中，界面保持为凸界面，利于单晶的生长［20］.随着凝固分数不断的增大，C值也不断增大，随着晶体长度的增加，界面发生形变现象.结合图2和图3可知，3个时期的界面C值分别为0.72、2.54和5.63 cm，说明在晶体生长的过程中，除生长末期，界面C值呈不断增大的趋势.

图2 不同生长时期的固-液界面位置和等温线分布

2.2 梯度区温度梯度对固-液界面的影响

图3为晶体生长过程中固-液界面凸度的变化趋势.

由图3可知，在15和20 K/cm温度梯度下的界面凸度C值的变化类似，界面均凸向液相区，界面的凸度均呈现先增大后减小的趋势.当温度梯度区的温度梯度为25 K/cm时，界面从凸向液相区到接近水平再凸向液相区的一个变化过程.在生长前期和生长中期，随着温度梯度的增加，界面的凸度呈现减小的趋势.但在生长末期，25 K/cm温度梯度下，界面的凸度大于其余两个温度梯度下的凸度.综合3条曲线来看，在同一梯度区温度梯度下，界面凸度在晶体生长中期出现最大值，此最大值随着梯度区温度梯度的增大而减小.随着梯度区温度梯度的增大，界面的凸度C值不断减小.

2.3 梯度区温度梯度对晶体生长速度的影响

图4为在r=0处，凝固分数和晶体瞬时生长速度的关系.凝固分数f，定义为生长晶体的长度ls和晶体总长度l的比值.晶体瞬时生长速度为［21］

式中：ks和km分别为固相和液相的热导率；Gs和Gm分别为凝固界面附近和固相中单位长度的温度梯度；ΔH为结晶潜热；ρs为固相密度.综合3条曲线，曲线的形状近似.随着凝固分数的增大，晶体的瞬时生长速度呈先增大后减小的趋势.由图4可知，固相和液相的热导率存在较大差异，导致晶体的瞬时生长速度大于坩埚下降速度.在凝固分数接近0或1时，晶体生长速度急剧增加，这种现象是由边缘效应所导致的.

图4 晶体生长过程中晶体生长速率（η）的变化

2.4 梯度区温度梯度对轴向温度分布和温度梯度的影响

影响坩埚中心轴的轴向温度分布和温度梯度的因素很多，固相和液相的长度、吸收系数以及热导率等均影响中心轴的轴向温度和温度梯度的分布.图5为晶体生长到150 h时，坩埚中心轴的位置和温度分布以及温度梯度的关系.

图5 坩埚中心轴的轴向温度分布和温度梯度分布

由图5可知，固相的温度梯度均小于液相的温度梯度.在界面附近，由于固相和液相的热导率以及吸收系数的差异导致温度梯度发生突变［16，22］.随着温度梯度增大，温度梯度突变点向下移动，且突变处的温度梯度差值增大.

2.5 梯度区温度梯度对径向温度分布和温度梯度的影响

界面处的径向温度分布和径向温度梯度如图6所示.由图6可知，3个不同的温度梯度下，坩埚边缘处的温度均高于中心轴处的温度，这是由于物料的热导率与坩埚热导率的差异所导致.界面处的温度分布均呈近似抛物线状，在靠近坩埚边缘处，由于边缘效应［23］，温度急剧增大.3个不同的温度梯度下，径向温度梯度均大于零.随r的增大，界面处径向的温度梯度呈逐渐增大的趋势.在靠近坩埚边缘处，温度梯度均呈现急剧增加.在径向（0～8 cm）范围内，径向温度梯度变化不大，这样有利于晶体的生长.在坩埚内壁边界处，随着温度梯度的增大，径向温度梯度呈现相同的增加趋势.在不同温度梯度下，径向温度与温度梯度分布近似.

图6 界面处的径向温度分布和温度梯度分布

2.6 辐射传热对轴向温度分布和温度梯度的影响

图7为晶体生长到100 h时，坩埚中心轴的位置和温度分布以及温度梯度的关系.

图7 坩埚中心轴的轴向温度分布和温度梯度分布

由图7可知，两条曲线中，固相的温度梯度均小于液相的温度梯度，并在界面附近处发生温度梯度突变.考虑晶体内部辐射的影响，温度梯度的突变点明显下移，且温度梯度呈现从先减小到突变再减小的变化过程.氟化钙晶体作为一种半透明的光学晶体，晶体内部辐射传热对晶体生长过程的传热具有重要的影响［8］.

2.7 实际晶体生长的实验结果

根据数值模拟结果，25 K/cm为适宜晶体生长的梯度区温度梯度.对单晶生长炉内部结构进行设计和调整，使梯度区的温度梯度为25 K/cm，在此条件下进行晶体生长实验，生长出的晶体如图8所示，晶体的直径为200 mm，等径段长度为100 mm.晶体完整，无宏观缺陷，内部无明显的散射颗粒，透明度好.

图8 CaF2晶体

3 结 论

通过数值模拟计算了垂直Bridgman法生长氟化钙晶体过程中的热传递，应用准稳态简化了计算过程.

1）计算结果表明：在3个不同时期（t=0 h，t=100 h，t=200 h），固相等温线的曲率小于液相等温线的曲率；在生长的前期和中期，随着温度梯度的增大，界面的凸度呈减小的趋势，但在生长末期，25 K/cm的温度梯度下，界面的凸度大于其余两个温度梯度下的凸度.

2）晶体的瞬时生长速度大于坩埚的下降速度，适当的调整坩埚的下降速度以获得平坦的生长界面.

3）在不同的温度梯度下，固相的温度梯度均小于液相的温度梯度.

4）考虑晶体内部辐射的影响，温度梯度的突变点明显下移，且温度梯度呈现从先减小到突变再减小的变化过程.

5）根据数值模拟结果，25 K/cm为适宜晶体生长的梯度区温度梯度.经过实际晶体生长实验.生长出的晶体完整，无宏观缺陷，内部无明显的散射颗粒，透明度好.

［1］ 甄西合，任绍霞，史达威，等.直径300 mm氟化钙晶体的生长［J］.人工晶体学报，2010，39（4）：1087-1088.

ZHEN Xihe，REN Shaoxia，SHI Dawei，et al.Growth of CaF2crystal with Φ300 mm［J］.Journal of Synthetic Crystals，2010，39（4）：1087-1088.

［2］ 段安锋，沈永宏，刘景和.大尺寸氟化钙单晶的光谱特性［J］.硅酸盐学报，2007，35（1）：85-87.

DUAN Anfeng，SHEN Yonghong，LIU Jinghe.Spectra of large-sized calcium fluoride single crystals［J］. Journal of The Chinese Ceramic Society，2007，35 （1）：85-87.

［3］ XU Jiayue，SHI Minli，LU Baoliang，et al.Bridgman growth and characterization of calcium fluoride crystals ［J］.Journal of Crystal Growth，2006，292：391-394.

［4］ MAWencheng，ZHAO Lili，DING Guoqiang，et al. Numerical study of heat transfer during sapphire crystal growthbyheatexchangermethod［J］. International Journal of Heat and Mass Transfer，2014，72：452-460.

［5］ BARVINSCHI F，STANCULESCU A，STANCULESCU F.Heat transfer process during the crystallization of benzil grown by the Bridgman-Stockbarger method ［J］.Journal of Crystal Growth，2011，317：23-27.

［6］ MOONEY R P，MCFADDEN S，GABALCOVÁ Z，et al.An experimental-numerical method for estimating heat transfer in a Bridgman furnace［J］.Applied Thermal Engineering，2014，67：61-71.

［7］ 李万万，桑文斌，闵嘉华，等.垂直布里奇曼法生长CdZnTe晶体时固液界面形状的控制［J］.半导体学报，2004，25（5）：535-541.

LI Wanwan，SANG Wenbin，MIN Jiahua，et al. Controlling solid-liquid interface configuration during crystal growth of CdZnTe by vertical Bridgman method［J］.Chinese Journal of Semiconductors，2004，25 （5）：535-541.

［8］ PLEIFFER M，MUHLBERG M.Interface shape observation and calculation in crystal growth of CdTe by the vertical Bridgman method［J］.Journal of Crystal Growth，1992，118：269-276.

［9］ LU Wenqiang.Boundary element analysis of the heat transferinBridgmangrowthprocessofsemitransparent crystals［J］.MaterialsScienceand Engineering，2000，A292：219-223.

［10］王思爱，苏小平，张峰燚，等.数字模拟法研究坩埚锥角对VGF法GaAs单晶生长的影响［J］.稀有金属，2011，35（4）：525-530.

WANG Siai，SU Xiaopin，ZHANG Fengyi，et al. Numerical simulation study on impact of cone angle of crucible on VGF GaAs monocrystal growth［J］. Chinese Journal of Rare Metals，2011，35（4）：525-530.

［11］史宏声，秦来顺，魏钦华，等.自发成核Bridgman法生长LaBr3：Ce晶体［J］.人工晶体学报，2010，37：231-233.

SHI Hongsheng，QIN laishun，WEI Qinhua，et al. Growth of LaBr3：Ce crystal by spontaneous nucleation Bridgman method［J］.Journal of Synthetic Crystals，2010，37：231-233.

［12］BARVINSCHI F，NICOARA I，SANTAILLERX J L，etal.Pseudo-transientheattransferinvertical Bridgman crystal growth of semi-transparent materials ［J］.Modelling Simul Mater Sci Eng，1998，6：691-700.

［13］VIZMAN D，NICOARA I，NICOARA D.On the factors affecting the isotherm shape during Bridgman growth of semi-transparent crystals［J］.Journal of Crystal Growth，1996，169：161-169.

［14］EDWARDS K，DERBY J J.Understanding horizontal Bridgmanshelfgrowthofcadmiumtellurideand cadmium zinc telluride I.Heat and momentum transfer ［J］.Journal of Crystal Growth，1997，79：120-132.

［15］彭岚，范菊艳，张全仕.分离Bridgman法晶体生长过程的影响因素［J］.工程热物理学报，2010，31 （4）：553-556. PENG Lan，FANJuyan，ZHANGQuanshi.The influence factor of the detached solidification Bridgman growth［J］.Journal of Engineering Thermophysics， 2010，31（4）：553-556.

［16］VIZMAN D，NICOARA I，MULLER G.Effects of temperature asymmetry and tilting in the vertical Bridgman growth of semi-transparent crystals［J］. Journal of Crystal Growth，2000，212：334-339.

［17］MOLCHANOV A，HILBURGER U，FRIEDRICH J，et al.Experimental verification of the numerical model for a CaF2crystal growth process［J］.Cryst Res Technol，2002，37（1）：77-82.

［18］陈瑞润，丁宏升，郭景杰，等.工艺参数影响冷坩埚熔铸Ti6Al4V温度场计算［J］.材料科学与工艺，2009，17（4）：482-486.

CHEN Ruirun，DING Hongsheng，GUO Jingjie，et al. Numericalcalculationoneffectofprocessing parameters on temperature field in continuous melting and solidification of Ti6Al4V alloys with cold crucible ［J］.Materials Science and Technology，2009，17 （4）：482-486.

［19］HUANGC E，ELWELL D，FEIGELSON R S.Influence of thermal conductivity on interface shape during Bridgman growth［J］.Journal of Crystal Growth，1983，64：441-447.

［20］介万奇.Bridgman法晶体生长技术的研究进展［J］.人工晶体学报，2012，41：24-35.

JIEWanqi.ProgressofBridgmancrystalgrowth technology［J］.Journal of Synthetic Crystals，2012，41：24-35.

［21］邢建东.晶体定向生长［M］.西安：西安交通大学出版社，2008.

［22］谷智，刘泉喜，介万奇.Hg1-xMnxTe晶体的垂直Bridgman法生长系统温度场分析［J］.红外技术，2010，32（5）：249-254.

GU Zhi，LIU Quanxi，JIE Wanqi.Numerical analysis of thermal field in a vertical bridgman crystal growth system of Hg1-xMnxTe［J］.Infrared Technology，2010，32（5）：249-254.

［23］丁国强，苏小平，屠海令，等.4英寸VGF GaAs单晶生长的数值模拟与实验研究［J］.稀有金属，2009，33（2）：211-216.

DING Guoqiang，SU Xiaoping，TU Hailing，et al. Numerical simulation and experimental study on 4″VGF GaAs crystal growth［J］.Chinese Journal of Rare Metals，2009，33（2）：211-216.

（编辑 吕雪梅）

Numerical simulation of heat transfer by vertical Bridgman method of CaF2single crystals growth

YAO Jing1，2，ZHOU Hai2，LU Yimin2，WAN Hancheng2

（1.School of Materials Science and Engineering，Beijing University of Chemical Technology，Beijing 100029，China；2.School of Materials Science and Engineering，Beijing Institute of Petrochemical Technology，Beijing 102617，China）

Finite element method is used to simulate heat transfer during the growth process of large size calcium fluoride by the vertical Bridgman method，the calculation process was simplified by the quasi-steady state model.The effects of different temperature gradient in gradient zone on interface shape and crystal growth rate were investigated.The impact of radiation on heat transfer was discussed.Simulation results show that curvature of the solid isotherm is less than the curvature of the liquid isotherm at three different periods. Convexity of interface changed during crystal growth process.Rate of crystallization and descent velocity of crucible were inconsistent.25 K/cm is suitable for temperature gradient of gradient zone.Radiation heat transfer inside the crystal has a major influence on the heat transfer of single crystal growth process.In light of simulation results，growth integrity，transparent crystals without macroscopic defects can be grown.

CaF2；finite element method；the vertical Bridgman method；numerical simulation；heat transfer；temperature field

O78

A

1005-0299（2015）04-0048-06

10.11951/j.issn.1005-0299.20150408

2014-02-26.

姚 静（1988—），男，硕士研究生.

周 海，E-mail：cookeyj88@gmail.com.