基于非线性投资策略的看涨期权定价模型

颜镜洲，冯长焕，罗德军，刘 群

(西华师范大学 数学与信息学院，四川 南充 637009)

本文以经典的欧式看涨期权定价理论为基础．在期权的有效期内，当股票的价格上涨并高于看涨期权的敲定价的时候，投资者会随股价的上涨而不断的买入股票，来规避风险．未来的股价高于敲定价的部分由卖方承担，卖方的风险可能非常大．经典定价理论假设的是期权持有人在期权的有效期内不进行股票交易，必须依靠看涨期权来规避风险．提高B-S 定价模型可以构造新的期权形式来进行规避风险，如:关卡期权，亚式期权，回望期权、芥末期权等［1-5］．文献［6，7］提出线性动态的投资策略的看涨、看跌期权的定价模型．本文在此基础之上提出了新的基于非线性的动态投资策略的看涨期权定价模型．基本的想法是投资者在购买股票看涨期权的同时还制定了一个按照股价走势确定的买入股票的投资策略，在期权有效期内，如果股价持续上涨并高于期权的敲定价，那么投资者能够在股票市场上按照预先假定下的非线性投资策略买入股票，从而能够减少股票投资的损失．也就是说按照非线性投资策略下的股票看涨期权的价格低于经典的看涨期权价格．

1 建立投资策略和损失函数

本文的符号和基本假设基于文献［6，7］:Q，投资者的持仓比例;A，总投资额;Q=购买股票的金额/A;S，股票的价格;K，看涨期权的敲定价;α，投资策略指数，表示购买股票的价格区间从K 上涨到(1 +α)K;β，资金的最高占用率，表示投资者购买股票的资金与总资金的之比的最大值．当股价从K 上涨到(1 +α)K，持股比例从0 上涨到β，其中:0≤β≤1，α≥0．假定投资者按照如下的非线性的增仓的投资策略

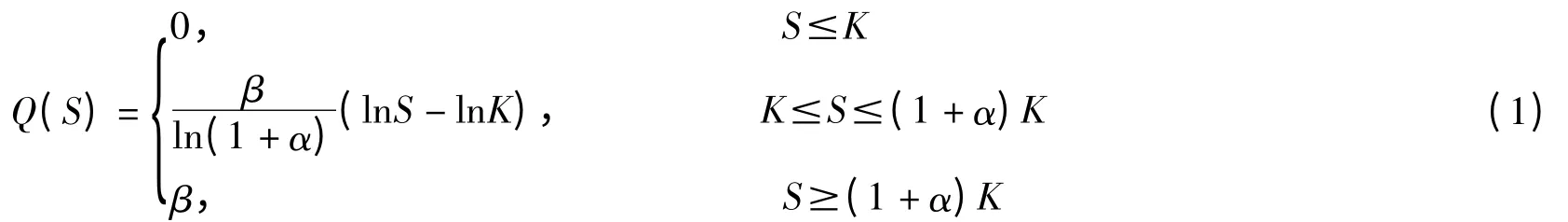
其中:α，为投资策略指数;β，为资金的最高占用比率．

当股票价格从S 变化到S+ΔS 时，购买股票资金的资金增加量为:ΔZ =ΔQ·A =A·Q(S)·ΔS，其中:ΔZ，购买股票资金的资金增加量，ΔQ，持股比例的变动量．

当股票价格上涨到S0时，当股票价格从S 变化到S +ΔS 时，购买股票的预期收益是其中预期的情况下增加资金购买的股票数．

当股票期权从K 上涨到S0，此时期权的预期收益为:

将上式积分化简可得:

假如股票期权从敲定价K 上涨到S0时，没有及时补仓，那么空仓时的预期损失为:

其中A/K :股票数，表示为敲定价为K 的时候，将全部的资金购买股票的数量．

假如期权投资者按照预定的非线性的持仓比例持股时，那么持有的股票可以减少一部分损失，损失为:

那么可以得到每股的损失为:

由于损失函数是基于投资策略下建立起来的，其收益函数等价于上述的损失函数:

2 看涨期权定价公式

利用Δ-对冲的技巧，通过构造投资组合能够得到Black-Scholes 偏微分方程［5］．其偏微分的形式为:

为了确定期权在合约有效期［0，T］的内价值，就要在区域∑={0≤S≤∞，0≤t≤T}上求解定解问题:

要解决上面定解问题，需要做变量替换:x=lnS，τ=T-t，

将定解问题(3)转化为常系数抛物型方程的Cauchy 问题:

作函数变换为:

在变换(6)下，(3)式转化为热传导方程

并且初值为:

可以用Poisson 公式［8］表示热传导方程(7)的Cauchy 问题的解:

其中φ(ξ)初值，K(x-ξ，τ)为热传导方程(7)的基本解:

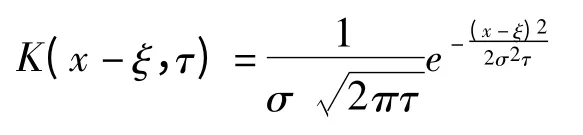
从而Cauchy 问题(7)(8)的解可以表示为:

将式(9)代入到V(x，τ)中可得:

为了形式简便我们记:V(x，τ)=Ⅰ1+Ⅰ2+Ⅰ3+Ⅰ4+Ⅰ5+Ⅰ6．

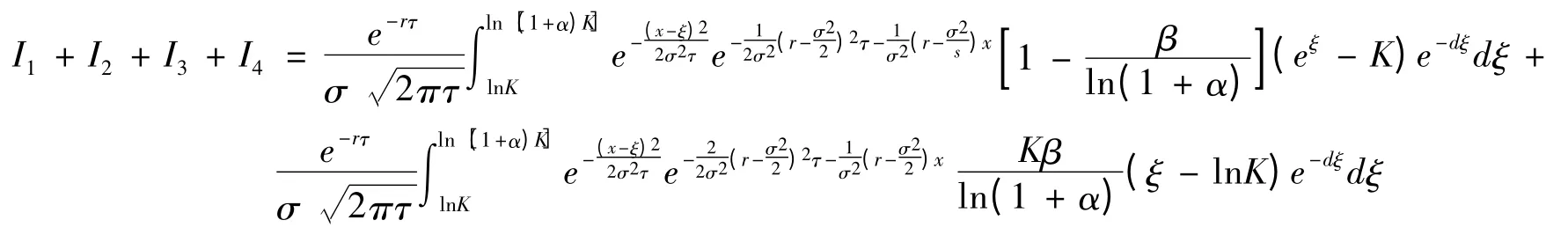
由于篇幅的限制略去了一些推导，需要推导的读者可以联系作者．继续用上述方法可得:

从而得到非线性投资策略下看涨欧式期权的定价模型:

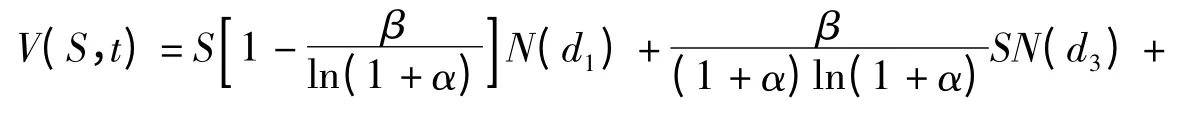
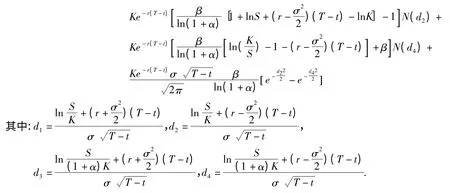
当α ＞0，β=0 时，投资者没有购买股票，这时候定价公式就退化为经典的Black-Scholes 公式V(S，t)=SN(d1)+Ke-r(T-t)N(d2)．

当β=0，α→0+时，可以从价值函数知道新期权在这个时候的价格便宜，投资者不需要期权来规避风险，只要主动在股票市场中买入股票来规避风险．容易计算得投资者的损失函数为0，进而得出收益函数为0．

［1］ BELLAMY N．Wealth optimization in an Incomplete Market Driven by A Jump-diffusion Process［J］．Journal of Mathematical Economics，2001，35(2):259 -287．

［2］ DIMITIES P，GEORGE S． Volatility options:Hedging Effectiveness，Pricing，and Model Error［J］． Journal of FuturesMarkets，2006，26(1):1 -31．

［3］ FEHLE F．Theory and Evidence on Option Exchange Design［J］．Journal of Futures Markets，2006，26(6):533 -570．

［4］ CASSAGNES A，CHENA Y，OHASHI H． Department Path Integral Pricing of Wasabi Option in the Black–Scholes Model［J］．Physica A 2014，413(11):1 -10．

［5］ 姜礼尚．期权定价的数学模型和方法［M］．第二版．北京:高等教育出版社，2008:255 -272，285 -311，74 -83．

［6］ WANG X，WANG L．Study on Black-Scholes Option Pricing Model Based on General Linear Investment Strategy(Part Ⅰ:put option)［J］．International Journal of Innovative Compufing，Information and Confrol，2009，5(8):2169 -2188．

［7］ WANG X，WANG L． Study on the Black-Scholes Stock Put Option Model Based on Dynamic Investment Strategy［C］．Proceedings of 2007 IEEE International Conference on Wireless Communications，Networking and Mobile Computing． IEEE Press，Shanghai． 2007:4128 -4131．

［8］ 姜礼尚．数学物理方程讲义［M］．第三版．北京:高等教育出版社，2006:116 -118．