基于过载法的船舶板架冗余度研究

吴剑国罗海东洪 英刘 俊师桂杰

（1.浙江工业大学 建筑工程学院 杭州 310014；2.中国船级社 上海规范研究所 上海 200135）

基于过载法的船舶板架冗余度研究

吴剑国1罗海东2洪 英2刘 俊1师桂杰2

（1.浙江工业大学 建筑工程学院 杭州 310014；2.中国船级社 上海规范研究所 上海 200135）

针对两种损伤模式，建立基于过载法的船舶板架结构冗余度计算模型，推导板架结构连续垮塌的最大屈曲利用因子计算公式。计算了6艘CSR船舶船底、内底板、舷侧板和甲板等板架损伤态的屈曲利用因子，验证船舶板架的冗余度。［关键词］结构冗余度；屈曲利用因子；扶强材垮塌

引 言

结构冗余度是指结构系统在某些构件受损或失效后能继续承受外载荷的能力。对于船舶与海洋工程行业来说，冗余度尚属于较新概念。制定海洋工程结构冗余度衡准的起因可追溯到1980年“Alexander L.Kielland”号平台的严重海损事故。仅仅由于一根关键承力支柱的疲劳破坏而引起一系列相邻支柱的连续失效，导致该平台在短短20分钟内倾覆沉没，造成人员及财产的重大损失。自20世纪80年代至90年代的20年里，散货船发生很多海损事故，共约有170艘散货船失事和1 300余名船员遇难，严峻的现实对海上结构特别是船舶结构的冗余度评估再次提出迫切要求。2006年，在国际海事组织（IMO）召开的海安会（MSC）上，散货船货舱与货物直接接触的所有板架结构抗垮塌评估已经得到证明和认可［1］。

IMO海安会决议（MSC.287（87） Resolution 7.3.1）的目标型标准（GBS）的符合性验证指南中［2］，明确提出这样一个命题 ——“按照规范设计的船舶是否具有足够的结构冗余度能够抵抗任何一个加筋构件的局部损伤？”并且IMO的《国际海上人命安全公约》（SOLAS）第12章中［3］，对散货船的结构冗余强度要求进一步描述：“货舱区域的结构应是这样的一个结构，即一个加筋构件的简单失效不会立即导致其他结构部件的连锁性失效，从而潜在地导致整个加筋板格的垮塌”。

IACS新制订的散货船和油船协调共同结构规范（CSR-H）［4］是否满足结构冗余度的要求，是业界关心的热点问题，也是IMO GBS评审的难点之一。

本文结合SOLAS公约［3］和CSR-H技术背景报告［4-5］，提出两种扶强材损伤的模型，推导出损伤评估准则，并对6艘CSR船舶板架的抗连续垮塌进行计算，应用过载法对这类区域板架结构冗余度进行验证探索。但冗余度符合性验证还是以基于非线性有限元分析的方法为准。

1 计算模型

加筋板的损伤是一种局部的机械性损伤，根据实船损伤的资料，归纳并假设以下两种损伤模式：

（1）扶强材的端部断裂，简化如图1所示；

图1 1号扶强材腹板断裂破损

（2）发生在一个6l /1 000的永久大变形，简化如图2所示。

s表示板格短边的长度；l表示板格长边的长度。

由于结构发生损伤与遭受最大载荷不会同时发生，暂时的结构损伤会在船舶检验中发现并被修复；因此可以认为发生局部损伤时，结构所承受的动态载荷将小于极限动态载荷。参照文献［1］，假设完整状态时的载荷为1.0S+1.0D，在损伤状态时的载荷为1.0S+0.8D，其中S代表静水载荷，D代表波浪动载荷。

令完整状态下扶强材的应力为σII，假设1号扶强材发生腹板断裂或发生6l /1 000的变形，破损状态下，破损的1号扶强材的应力为σDD，毗邻损扶强材的2号、3号扶强材（见图1、图2）的应力为σID。根据CSR-H规范，扶强材的屈曲应力公式为：

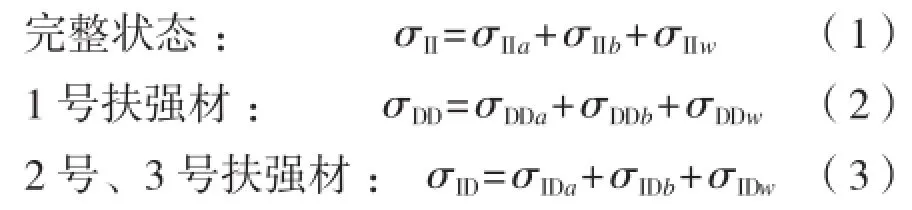
式中：第一个下标I表示完整结构，D表示损伤结构；第二个下标I表示完整状态的载荷，D表示损伤状态的载荷；第三个下标a表示轴向均布压应力，下标b表示弯曲应力，下标w表示扭转变形应力。

2 冗余度评估准则

按照CSR-H的描述性方法，采用屈曲利用因子η，衡量屈曲强度的衡准是：如果满足下式，则认为结构具有可接受的屈曲强度：

式中：η为基于所使用设计载荷的实际屈曲利用因子；ηall为许用屈曲利用因子，其值取1。

对于组合载荷，屈曲利用因子η定义为施加的等效应力和相应的屈曲能力之比，计算公式如下：

式中：γc为结构发生破坏时的应力乘子系数，对于扶强材屈曲有以下公式：

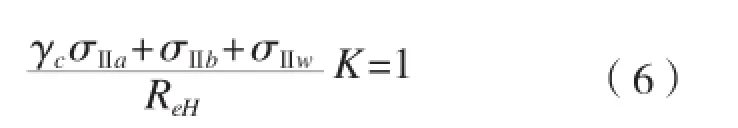
式中：K为安全因子，对于油船和散货船非货物接触区域，K=1；其余符号同上。

根据SOLAS公约XII/6.5.1和6.5.3［1］可知：一根扶强材发生损伤，工作应力有所增加，如果应力达到屈服或屈曲条件，超过的应力将作为载荷转移到紧邻的两根扶强材上，要求邻近的两根扶强材在“ 工作载荷+转移来的载荷”作用下，仍能具有足够的屈曲强度。如图1、图2所示，假设1号扶强材发生破损或大的变形。在损伤状态下，如果该扶强材的应力σDD超出屈服应力ReH，超出的部分为=σDD-ReH。若该应力被平均分配给相邻的2、3号扶强材上，则2号、3号扶强材的应力由σID增大到根据抗连续垮塌的要求，在损伤状态下，1号扶强材的损伤不应导致2号、3号扶强材的屈曲应力超过屈服应力。

根据以上推导可得油船和散货船非货物接触区域的扶强材的屈曲评估准则：

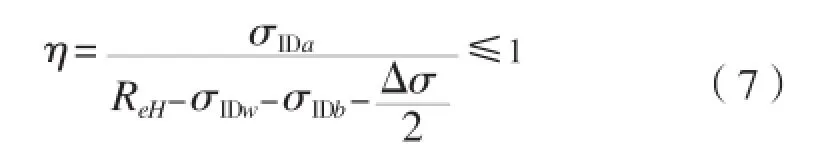
3 抗连续垮塌计算公式

3.1 扶强材效轴向应力和扭转应力计算

据CSR-H［3］，扶强材的有效轴向应力：

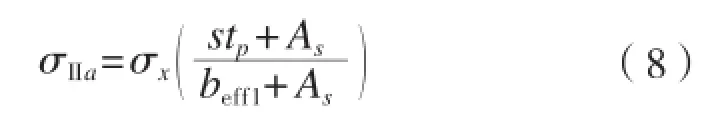
式中：σx损伤状态下名义应力，N/mm2；s表示板格短边的长度，mm；tp为净板厚，mm；As为扶强材的净截面面积，mm2；beff1为扶强材带板的有效宽度，mm。

由于抗连续垮塌问题重点是研究纵骨架式板架短边受压的工况，取：

式中：σhg为船体梁弯曲应力，N/mm2；Wz为船体横剖面的净剖面模数，cm3；Ms、Mw分别为船中静水弯矩和波浪弯矩，kN·m。

由于轴向应力主要是取决于总纵应力，与扶强材的边界和挠度无关，因此认为损伤不影响扶强材的轴向均布压应力，即：

据CSR-H［3］，扶强材的扭转屈曲应力：

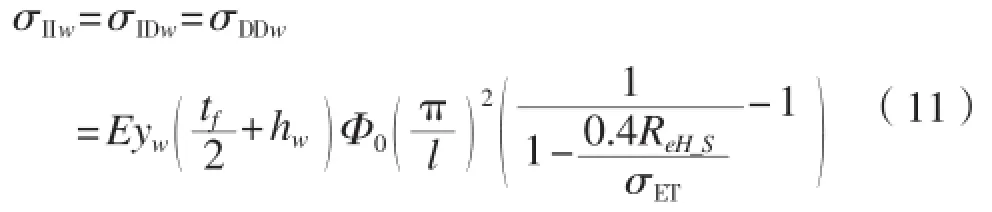
式中：yw为扶强材截面型心至扶强材翼缘自由边的距离，mm； Φ0为系数；σET为扭转屈曲的参考应力；其他符号同上。

3.2 扶强材弯曲应力计算公式

扶强材的弯曲应力：

式中：M1是侧向载荷作用下扶强材的弯矩，N·mm；M0是挠度变形引起的弯矩，N·mm。Z为扶强材的净截面模数，cm3。

3.2.1 扶强材腹板断裂

对于未损伤的2号、3号扶强材的计算模型简化为两端固支的梁，如图3所示；对于损伤的1号扶强材的计算模型简化为一端简支，一端固支的梁，如图4所示。

图3 扶强材的两端固支

图4 扶强材的一端简支，一端固支

根据图3、图4，侧向载荷作用下扶强材的弯矩分别为：

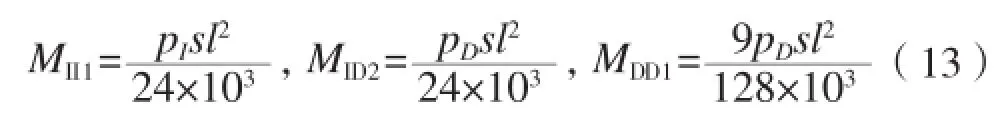
式中：pI为完整状态下的侧向载荷，kN/m2；pD为损伤状态下的侧向载荷，kN/m2；s为扶强材间距，mm；l为扶强材跨距，mm。公式中M下标的含义同上。

根据图4，损伤状态侧向载荷作用下扶强材的挠度wDD1，将wDD1代入完整状态下挠度变形引起的弯矩M0中可以求得损伤状态下扶强材的挠度变形引起的弯矩为：

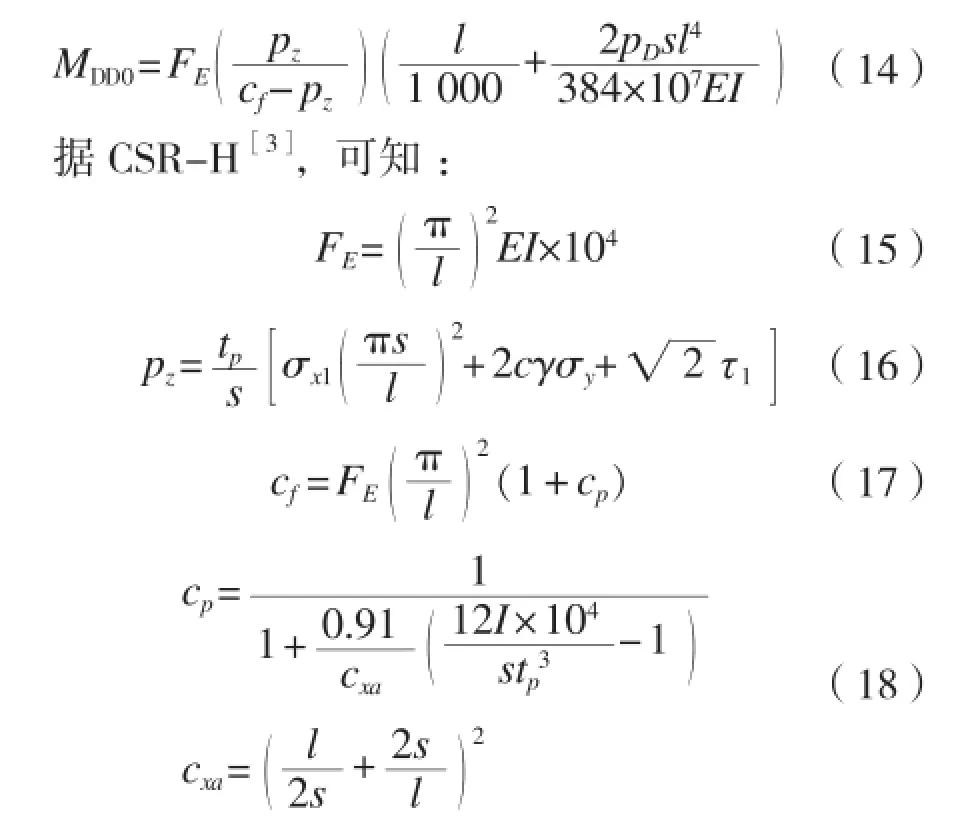
式中：FE为扶强材的理想屈曲应力，N；EI为扶强材的弹性模量，N·mm2；pz为名义侧向荷载，N/mm2；cf为扶强材提供的弹性支撑，N/mm2；。

将式（13）和式（14）代入式（12）中可得扶强材腹板断裂时的弯曲应力σDDb。

3.2.2 扶强材变形

挠度计算公式为：

式中：w0为扶强材的假定缺陷引起的6l/1 000位移，mm；w1为扶强材变形引起的位移，mm。

所有扶强材的计算模型都简化为两端固支的梁，如图3所示。计算出侧向力作用下的扶强材变形wDD1，将wDD1代入到完整状态下挠度变形引起的弯矩M0中，可以求得损伤状态下扶强材的挠度变形引起的弯矩MDD0为：

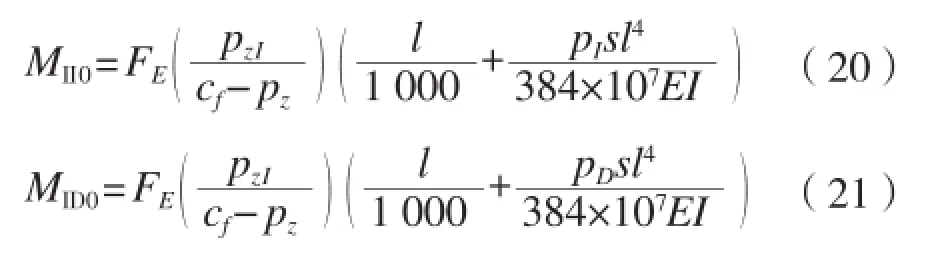
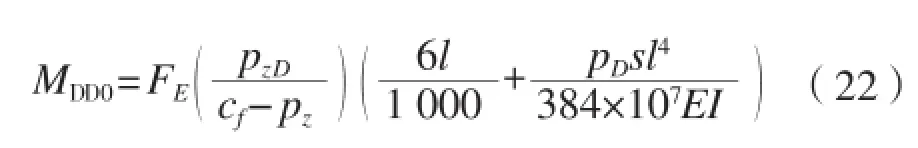
式中：符号同上。

对于损伤的1号扶强材和未损伤的2号、3号扶强材的计算模型简化为两端固支的梁，如图3所示；获得大变形时侧向载荷作用下扶强材的弯矩MDD1：

式中：符号同上。

将式（22）和式（23）代入式（12）中可得扶强材大变形时的弯曲应力 。

4 抗连续垮塌实船验证

进行了3艘CSR油船和3艘CSR散货船的船中剖面完整工况和破损工况下各类板架扶强材的轴向应力、扭转应力和扶强材弯曲应力计算，计算出破损扶强材，毗邻扶强材和远处扶强材的屈曲利用因子。根据毗邻扶强材的利用因子准则式（4），判定其是否屈曲失效。限于篇幅，本文仅列出1艘CSR油船货船区域各处的板架计算结果如图5、图6所示。

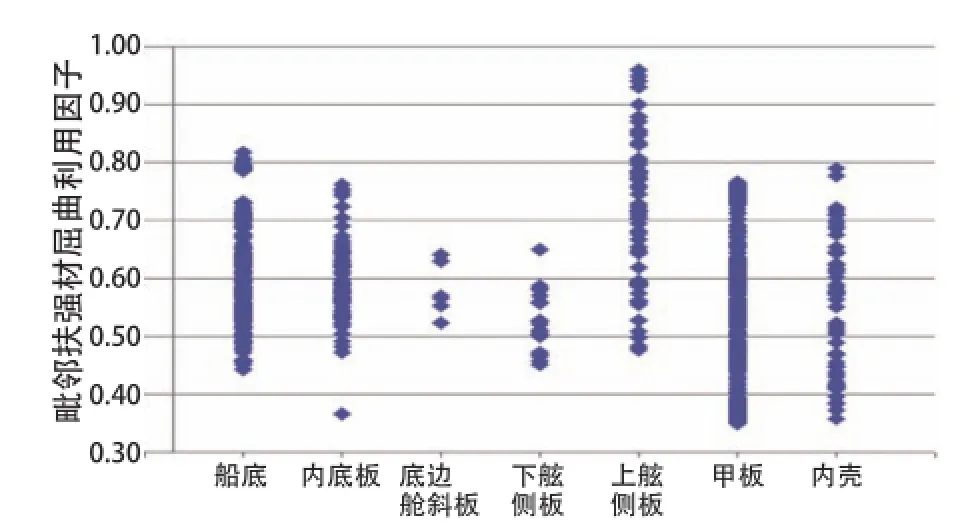
图5 毗邻大变形扶强材的屈曲利用因子

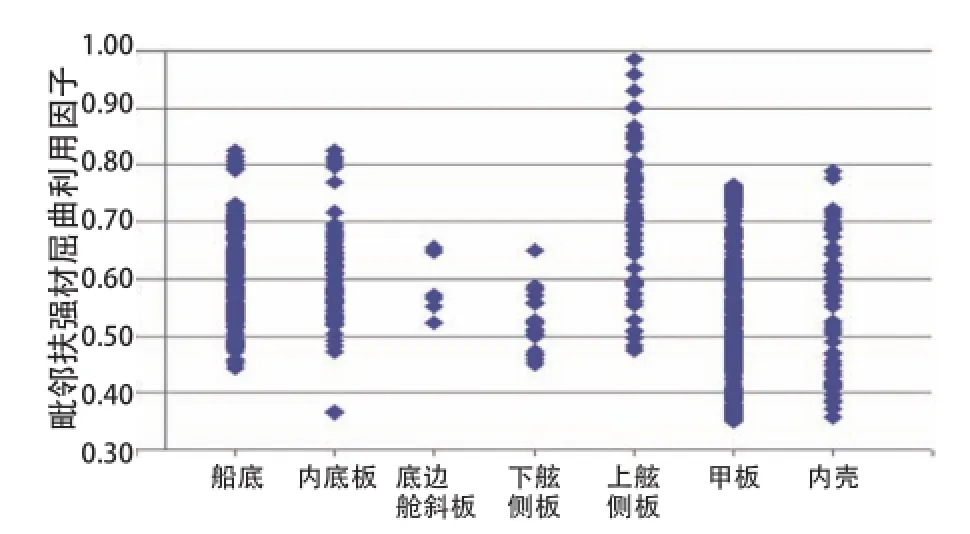
图6 毗邻腹板断裂扶强材的屈曲利用因子

破损扶强材、毗邻扶强材和远处扶强材的最大屈曲利用因子对比柱形图如图7、图8所示。

图7 永久大变形后扶强材的最大屈曲利用因子

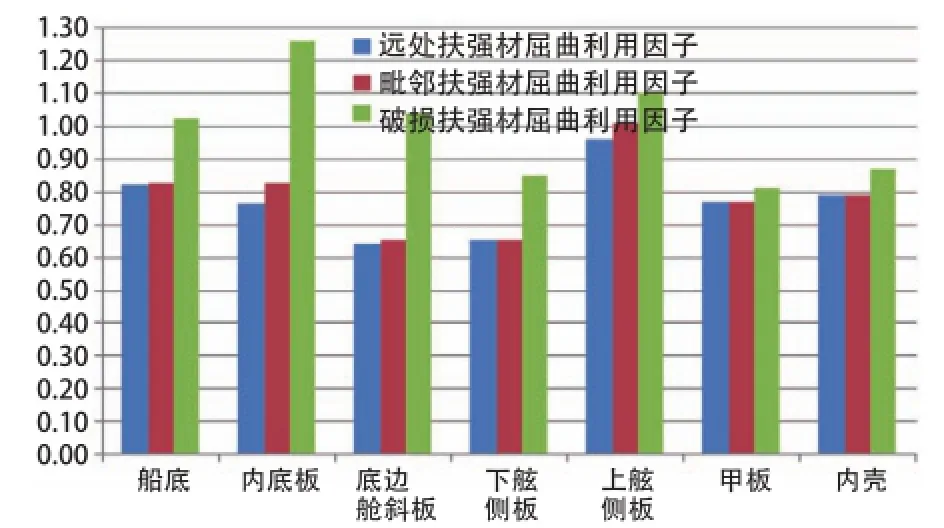
图8 腹板断裂后板架的最大屈曲利用因子

汇总6艘CSR船货舱区域各处的板架在不同工况下，3艘油船的一根纵向扶强材发生永久大变形和腹板断裂的毗邻扶强材最大屈曲利用因子如图9和图10所示，3艘散货船的一根纵向扶强材?发生永久大变形和腹板断裂的毗邻扶强材最大屈曲利用因子如图11和图12示。可以看出，所有扶强材屈曲利用因子均满足屈曲要求，板架结构具有足够的冗余度。

图9 油船扶强材变形后的板架屈曲利用因子

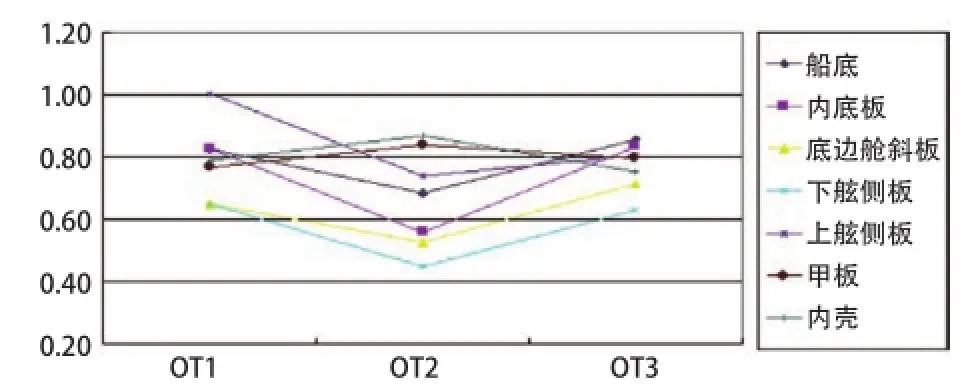
图10 油船扶强材腹板断裂后的板架屈曲利用因子

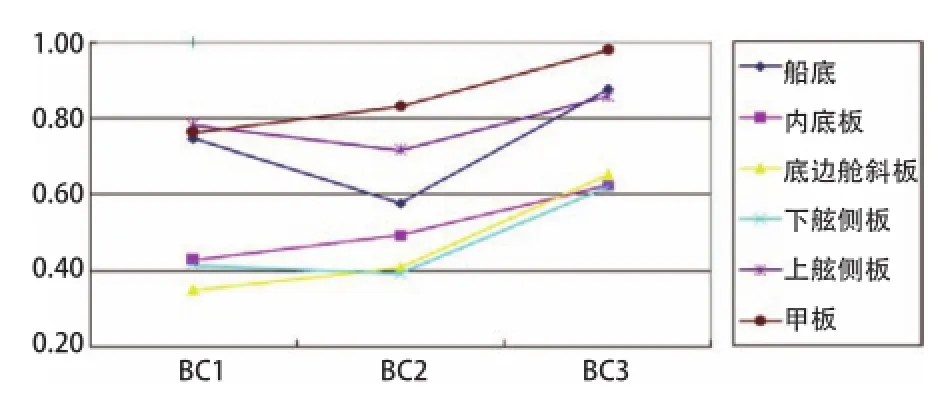
图11 散货船扶强材变形后的板架屈曲利用因子

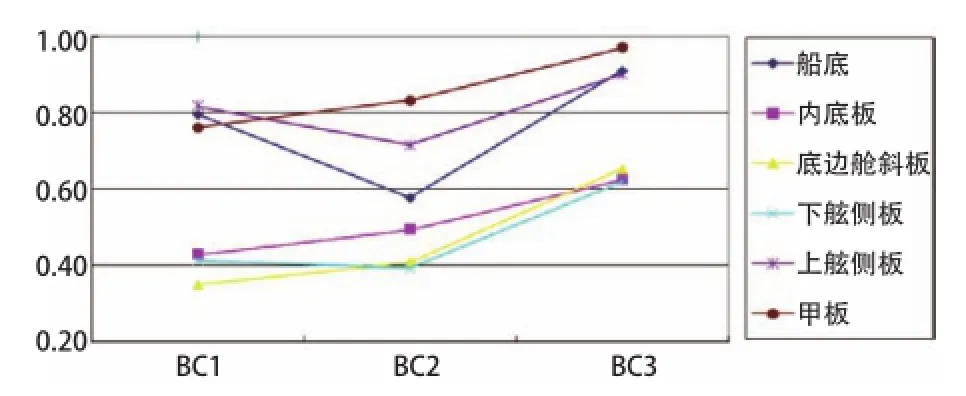
图12 散货船扶强材腹板断裂的板架屈曲利用因子

5 结 论

采用本文的船舶板架结构冗余度计算模型，计算了6艘CSR船舶的屈曲利用因子，均未发现毗邻损坏扶强材出现屈曲因子超标现象。因此得出结论，按照CSR-H设计的板架结构具有足够的冗余度，不会发生连续垮塌现象。

［1］ IMO SLS.14/Circ.250-Unified Interpretations of Regulations XII/6.5.1 and XII/6.5.3 of the 1974 SOLAS Convention as Amended by Resolution MSC.170（79）， 2005.

［2］ IMO MSC.287（87） -Adoption of the International Goalbased Ship Construction Standards for Bulk Carriers and Oil Tankers， 2010.

［3］ IACS. Common Structural Rules for Bulk Carriers and Double Oil Tankers， 2014.

［4］ IACS. Technical Backgrounds Report： “Structural Redundancy”， 2014.

［5］ IACS. Technical Backgrounds - Structural Redundancy Requirements of SOLAS Regulation XII/6.5.1 and 6.5.3 in CSR for Bulk Carriers， 2005.

Research about structural redundancy of grillage stiff ener based on over load method

WU Jian-guo1LO Hai-dong2HONG Ying2LIU Jun1SHI Gui-jie2
(1. College of Architectural & Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, China; 2. Shanghai Rules Research Institute, CCS, Shanghai 200135,China)

For two damage assumption conditions， the computational model for the structural redundancy of a ship grillage stiff ener is developed. A formula for maximum buckling utilization factor is derived， which is applicable for progressive collapse of ship structure grillage stiff ener. The calculation results of 6 actual bulk carriers and oil tankers designed by CSR-H show that the actual ships satisfy the evaluation criteria of structural redundancy.

structural redundancy； buckling utilization factor； stiff ener collapse

U661.3

A

1001-9855（2015）06-0101-05

2015-06-22

吴剑国（1963-），男，博士，教授，研究方向：船舶结构。

罗海东（1964-），男，高级工程师，研究方向：船舶规范研究。

洪 英（1963-），男，高级工程师，研究方向：船舶规范研究。

刘 俊（1989-），男，硕士，助理工程师，研究方向：结构工程。

师桂杰（1984-），男，博士，高级工程师，研究方向：船舶规范研究。