积分变限函数求导研究

常安成 湖南信息学院

积分变限函数求导研究

常安成 湖南信息学院

本文先回顾积分上限函数的求导问题，然后由易至难逐步研究一些较为复杂的变限函数的求导问题，最后得到一个重要的定理。

变限函数 函数求导 分离变量函数

为了介绍牛顿——莱布尼兹公式，我们引入了积分上限公式函数。这是一个很重要的函数，有着很好的性质，只要在上连续，就一定有可导，且有求导公式。可以看出函数是函数的一个原函数，这就解决了不定积分中没能证明的结论：连续函数必有原函数。容易推出。下面我们对更一般的积分上限函数（或称变限函数）的求导作进一步的研究。

一、变限函数的导数

所以由复合函数求导法则可得

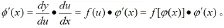
二、变限函数的导数

那么它的导数可用乘积的求导法则解决：

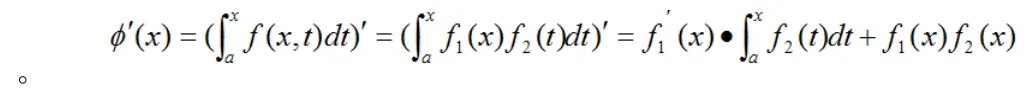
这是一个相当抽象的函数，我们知道对于抽象函数的求导一般使用定义来求函数增量：

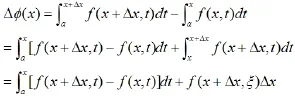
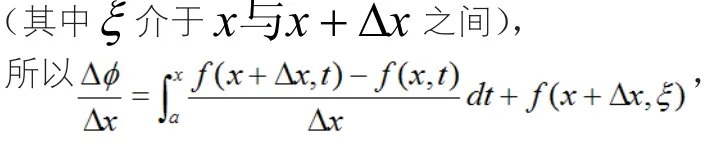
三、研究结论

从上面的情况分析，我们可以得出本文研究所得的结论：

我们现在应用这个定理来解答一道题，并也用分离变量的方法解答此题，以此来对比这两个方法解题的效果如何。

方法一：应用定理解答

有定理得：

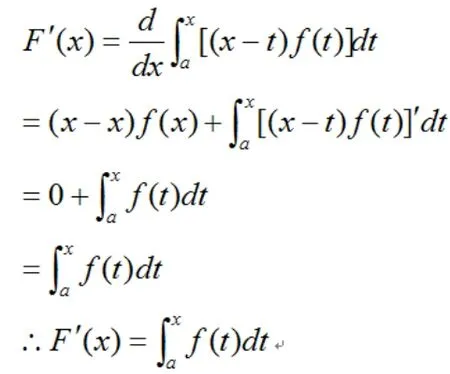
方法二：应用分离变量的方法解答

解：因为

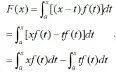
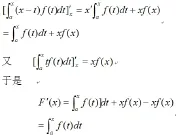
从以上解题效果看，用定理解题要比用分离变量的方法解题简单方便快捷。况且，定理既可以应用于可分离变量的情况，又可应用于不可分离变量的情况。此定理对于解决复杂的积分变上限函数的求导给予了一种便捷的解法，以供参考。