STRONG LAW OF LARGE NUMBERS AND GROWTH RATE FOR NOD SEQUENCES

MA Song-linWANG Xue-jun

（1 College of Applied Mathematics，Chaohu College，Chaohu Anhui 238000）

（2 School of Mathematical Sciences，Anhui University，Hefei Anhui 230039）

STRONG LAW OF LARGE NUMBERS AND GROWTH RATE FOR NOD SEQUENCES

MA Song-lin1WANG Xue-jun2

（1 College of Applied Mathematics，Chaohu College，Chaohu Anhui 238000）

（2 School of Mathematical Sciences，Anhui University，Hefei Anhui 230039）

In the paper，we get the precise results of Hájek-Rényi type inequalities for the partial sums of negatively orthant dependent sequences，which improve the results of Theorem 3.1 and Corollary 3.2 in Kim（2006）and the strong law of large numbers and strong growth rate for negatively orthant dependent sequences.

negatively orthant dependent sequences；strong law of large numbers growth rate

I Introduction

We use the following notations.Letbe a sequence of random variables defined on a fixed probability space.Denote

Hájek-Rényi（1955）proved the following important inequality.Ifis a sequence of independent random variables with mean zero，andis a nondecreasing sequence of positive real numbers， then for any ε＞0 and any positive integer m＜n，

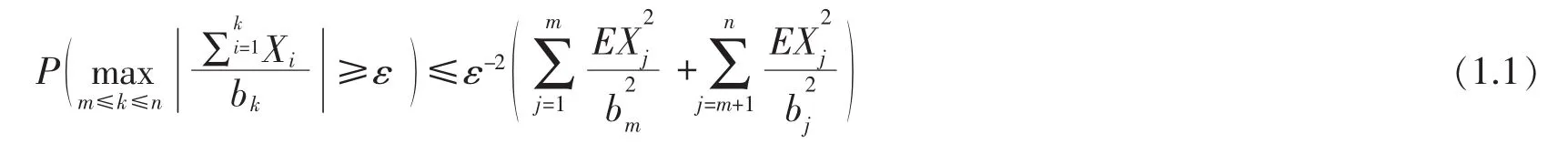
In the paper，we will further study Hájek-Rényi type inequality for negatively orthant dependent sequences and give the better coefficient（4ε-2（log3n+2）2）than that（8ε-2（log3n+2）2）in Kim（2006）and the condition＜∞in Kim（2006）can be removed.In addition we obtain the the strong law of large numbers and strong growth rate for negatively orthant dependent sequences.

Definition 1.1

A finite collection of random variables X1，X2，…，Xnis said to be negatively upper orthant dependent（NUOD），if for all real numbers x1，x2，…，xn，

and negatively lower orthant dependent（NLOD）if for all real numbers x1，x2，…，xn，

A finite collection of random variables X1，X2，…，Xnis said to be negatively orthant dependent（NOD）if they are both NUOD and NLOD.

Lemma 1.1 （cf.Bozorgnia et al.，1996）.Letbe a sequence of NOD random variables， f1，f2… be all nondecreasing（or all nonincreasing）functions，thenis still a sequence of NOD.

Lemma 1.2 （cf.Kim，2006）.Let X1，X2，…，Xnbe NOD random variables with EXn=0 and EX2n＜∞for all n≥1.Then we have

for all integers m，p≥1，m+p≤n.Moreover，we have

By Lemma 1.1 and Lemma 1.2，we can get the following corollary.

Lemma 1.3（cf.Hu，et al.，2008，Lemma 1.5）.Letbe a random variables.Letbe a nondecreasing unbounded sequence of positive numbers and α1，α2，… be nonnegative numbers.Let r and C be fixed positive numbers.Assume that for each n≥1

Lemma 1.4 （cf. Fazekas and Klesov，2001，Corollary 2.1）.Letbe a nondecreasing unbounded sequence of positive numbers and α1，α2，…be nonnegative numbers.Denote.Let r be a fixed positive number Satisfying（1.7）.If

then（1.9）-（1.14）hold.

II Hájek-Rényi type inequalities for NOD

In this section，we will give Hájek-Rényi type inequalities for NOD sequences，which improve the results of Kim（2006）.

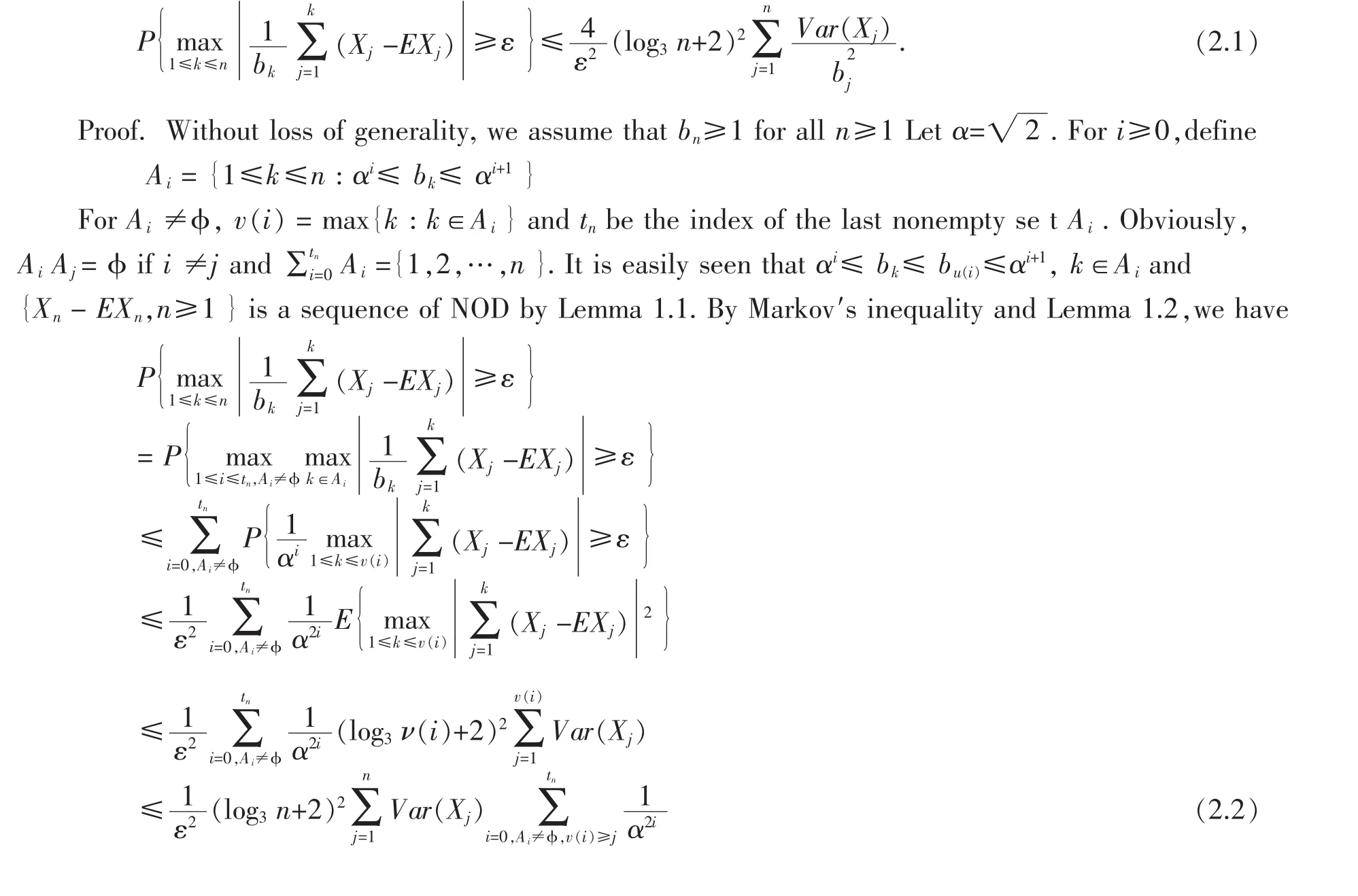
III SLLN AND GROWTH RATE FOR NOD

Assume that

That is to say（1.15）holds.By Remark 2.1 in Fazekas and Klesov（2001），（1.15）implies（1.16）.By Lemma 1.4，we can obtain（3.12）-（3.17）immediately.

Remark 3.1. In this section，not only the strong laws of large numbers are obtained，but also the strong growth rate are given.So our results improve some corresponding results for NOD sequences in Kim（2006）.

［1］Bozorgnia，A.，Patterson，R.F.，Taylor，R.L..Limit theorems for dependent random variables［C］.World Congress Nonlinear Analysts’92，1996：1639-1650.

［2］Christofides，T.C..Maximal inequalities for demimartingales and a strong law of large numbers［J］.Statist.Probab.Lett.，2000，（50）：357-363.

［3］Fazekas，I.，Klesov，O..A general approach to the strong law of large numbers［J］.Theory Probab.Appl.，2001，（45）：436-449.

［4］Gan，S.X..The Hájek-Rényi inequality for Banach space valued martingales and the p smoothness of Banach space［J］.Statist. Probab.Lett.，1997，（32）：245-248.

［5］Hájek-Rényi，A..A generalization of an inequality of Kolmogorov［J］.Acta Math.Acad.Sci.Hungar.，1955，（6）：281-284.

［6］Hu，S.H.，Chen，G.J.，Wang，X.J..On extending the Brunk-Prokhorov strong law of large numbers for martingale differences［J］. Statist.Probab.Lett.，2008，（78）：3187-3194.

［7］Hu，S.H.，Wang，X.J.，Yang，W.Z.，Zhao，T..The Hájek-Rényi type inequality for associated random variables［J］.Statist. Probab.Lett.，2009，（79）：884-888.

［8］Joag-Dev，K.，Proschan，F..Negative association of random variables with applications［J］.Ann.Statist.，1983，（1）：286-295.

［9］Kim，H.C..The Hájek-Rényi inequality for weighted sums of negatively orthant dependent random variables［J］.Int.J.Contemp.Math.Sci.，2006，（6）：297-303.

［10］Liu，J.J.，Gan，S.X.，Chen，P.Y..The Hájek-Rényi inequality for NA random variables and its application［J］.Statist. Probab.Lett.，1999，（43）：99-105.

陈 侃

O211.4 Document code：A Article ID：1672-2868（2015）03-0001-06

Eceived date：2015-03-03

Fund Project：Foundation of Anhui Educational Committee（No.KJ2013Z225）

Author：Ma Songlin（1978-），male，Lujiang，Anhui Province，Scool of Applied Mathematics，Chaohu College.Research direction：probability limit theory.