基于分形市场理论的动量生命周期研究

■吴 栩，宋光辉，钱崇秀

一、引言

动 量 生 命 周 期 （Momentum Life Cycle） 由Bernstein（1993）公之于世。动量生命周期以DeBondt和 Thaler(1985)、Jegadeesh 和 Titman(1993)的反转和动量效应为基础，特别强调证券价格中的动量和反转效应会相互转换。如今，证券价格存在动量生命周期现象已被 Lee和 Swaminathan （2000）、Ding et al.（2008）、Asness et al.（2013）等众多学者所认可。然而， 正如 Moskowitz et al.（2012）、Andrei和 Cujean（2014）、宋光辉等（2014）等学者所言，现有研究倾向于将动量和反转效应割裂开来进行研究；虽然许多学者利用行为金融理论和经典金融理论对动量和反转给出了众多的解释，但难以从中窥视动量和反转效应的相互转换关系；从而，难以分析动量和反转效应的持续时间，进而难以辨别动量和反转效应，最终难以提升动量和反转投资策略的有效性。那么，如何解释动量和反转效应的转换关系呢？即有什么理论可以解释动量生命周期现象呢？下文对此进行探讨。

二、模型构建与分析

证券价格序列存在的动量生命周期现象与投资者的交易行为密切相关。Franck et al.(2013)、Ahmed(2014)等学者实证发现，实践中投资者普遍采用动量和反转交易，且动量和反转交易分别对动量和反转效应具有强化作用。对于投资行为的选择倾向，Peters（1994）在创立分形市场理论（Fractal Market Theory,FMT）时指出，投资者有限理性；且投资者对信息的敏感程度复杂多变，时而注重短期价格信息，倾向于采用追涨杀跌的动量交易；时而又注重长期价格信息，倾向于采用低吸高抛的反转交易；最终导致证券价格出现分形特征。时至今日，FMT已得到了Zunino et al.(2008)和宋光辉等(2013)等众多学者的实证支撑，FMT对投资者行为的描述较为符合实际情况。下文首先根据FMT做出假设H1和H2,随后以此为基础，将投资者投资决策过程模型化，进而利用其对动量生命周期中的动量和反转效应的相互转换展开分析。

H1：投资者有限理性，其投资目的在于获取正的资本利得，其选择成功率最高的投资策略进行实际投资，但投资者对证券价格序列的关注长度或对投资策略成功率的记忆长度有限。设投资者i在时刻t对证券价格时间序列关注长度为 m（t）,对动i量或反转投资策略 si，m（t）的成功率（t） 的记忆长度为 hi（t）,则投资者 i在时刻 t接受的价格序列为也只能记住从第 t-h（t）期到i第t-1期策略的成功率，并选择成功率最高的策略进行投资实践。

H2：投资者对信息的敏感程度存在复杂性，设Mi（t）=hi（t）-1×Σmi（k）为投资者 i在时刻 t之前对价格序列关注长度的均值，则当 mi（t）≤Mi（t）或 mi（t）＞Mi（t）时，投资者分别从动量策略集（t）或反转策略集（t）中选取动量策略或反转策略进行投资行动。

（一）投资过程模型构建

投资策略，即根据符号序列进行投资行动的准则。用1和-1分别表示投资者买入和卖出证券，即行动集A={1，-1},则投资者i在时刻t的备选投资策 略 为 {U|U ∩Xi（t）}到 行 动 集 A 的 映 射 ， 共 22li（t）-1种。对于复权的证券价格序列，在卖空限制下，唯有通过低买高卖方可获得正的资本利得，其主要的操作形式便是以低吸高抛为特征的反转策略和以追涨杀跌为特征的动量策略。因而为了表述的方便，对于所有 22li（t）-1种备选投资策略，不妨直接记 SMim（t）对应的行动记为 Ai，m（t）∈A.

反转策略的特征在于低吸高抛。投资者利用反转策略买入或卖出的关键在于其认为此时供过于求或供不应求，买入或卖出具有价格优势；因而，投资者争当t时刻的少数派是利用反转策略实现投资获利的保障。假设t时刻所有N位投资者均采用反转策略，记投资者i的交易量为Vi（t），成功率最高的投资策略所对应的实际行动为 Ai（t），sgn[]为符号函数，则根据H1以及Challet et al.(2000)的少数派博弈模型，此时投资者i遴选反转策略进行实际行动的过程可用如下(1)式至(3)式表述：

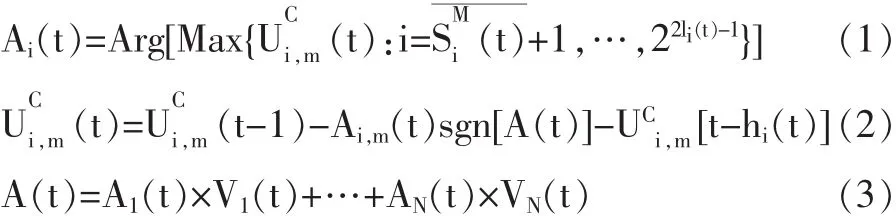
动量策略的特征在于追涨杀跌。投资者利用动量策略买入或卖出获利的关键在于证券价格在t+1时刻仍上涨或下跌，即在t+1时刻有更多的投资者买入或卖出。因而，投资者争当t+1时刻的多数派是依赖动量策略实现投资获利的保障。假设t时刻所有投资者均采用动量策略，则根据H1及Andersen和Didier(2003)的多数派博弈模型，投资者i在时刻t遴选动量策略进行实际行动的过程可用如下(4)式至(5)式表述：

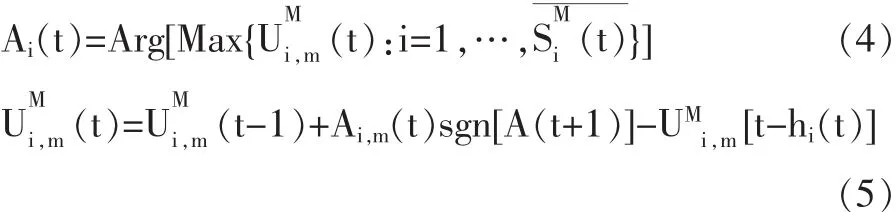
上述(1)式至(3)式或(4)式至(5)式所描述的策略遴选过程，以所有投资者同时使用动量或反转策略为假设前提，这背离了Ahmed(2014)所揭示的现实情况。对此背离，根据FMT提出的H2提供了解决之道，投资者在动量和反转策略中动态选择。当投资者i 在 t时刻对价格序列关注的长度 mi（t）≤Mi（t）时，投资者根据(4)式至(5)式所示的博弈过程从动量策略集SMi（t）遴选动量策略进行投资行动；反之，当投资者对价格序列关注的长度 mi（t）＞Mt（t）时，则投资者根据(1)式至(3)式所示的博弈过程从反转策略集SCi（t）选取反转策略进行投资实践。根据FMT提出的H1和H2为投资者的策略选择过程提供了多样性和复杂性，投资者对信息的有限关注或记忆，以及对信息敏感度的差异致使投资决策过程逼近现实情况。

（二）动量生命周期理论分析

投资者通过上述投资决策过程所做出的行动通过 Ai（t）体现，而式(3)所示的证券过度需求 A（t）正是所有投资者决策结果的汇总。根据H2和决策过程，投资者行为选择的动态性使得行动Ai（t）∈A具有不确定性。 当假设交易量 Vi（t）=1 时，由 Ai（t）汇集而成的A（t）便在[-N，N]中波动。根据刘兴华和杨建梅(2007)研究可知，证券价格Pt与过度需求A（t）有关系存在。因此，当 A（t）＞0 时，有 Pt+1＞Pt，即价格上涨；当 A（t）＜0 时，有 Pt+1＜Pt，即价格下跌。因而，当证券过度需求 A（t）＞0 或 A（t）＜0 持续出现时，价格持续上涨或下跌，表现出动量效应；当A（t）＞0或A（t）＜0持续性受到破坏时，价格上涨或下跌趋势发生反转，进而产生反转效应。投资者的动态行为选择驱使 A（t）在[-N，0]和[0，-N]中游荡，进而驱使动量和反转效应相互转换，使得证券价格表现出动量生命周期。

三、仿真分析

理论分析显示，市场中所有投资者在假设H1和H2下的投资行动汇集后使得证券过度需求A（t）在[-N，0]和[0，-N]中游荡，引发证券价格序列中存在动量生命周期现象。为了更加简单明了地体现上述理论决策过程所产生的价格序列与真实的价格序列具有相似的动量生命周期现象，以下根据理论模型进行仿真分析。为了形象，下图1简要罗列了上述理论模型所描绘的仿真步骤。

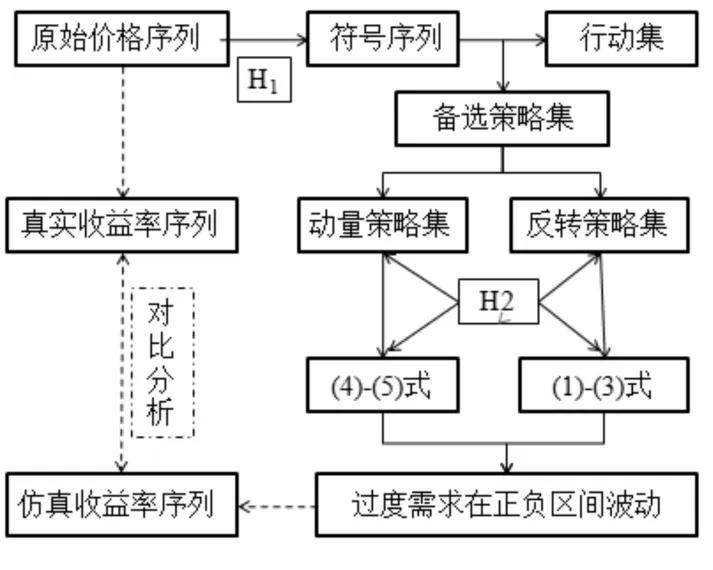
图1 仿真步骤简图

在利用Matlab7.0和SPSS 18.0进行具体的仿真分析时，本文以上交所所有行业指数日收盘价作为真实价格序列，数据来源于聚源数据库。样本区间选为2004年1月2日至2014年1月30日，该区间包含了完整的市场周期。仿真过程中，取N=1001,hi（t）=3,mi（t）≤3,ci（t）=0.005;并且，当出现策略成功率相同的情形时，如所有策略的初始成功率全为0，此时，假设投资者在这些策略中随机选择。对仿真和真实对数收益率序列进行比较分析时，本文使用对所有行业指数的仿真和真实值取平均的技巧避免上述随机选择引致的随机性。与此同时，由于若两个序列的对数收益率相似，则其价格序列将表现出相似的动量生命周期现象；因此，对比分析仿真结果与实际情况时，只需对仿真和真实对数收益率序列进行比较分析。真实与仿真对数收益率序列的描述性统计见下表1。

表1 真实和仿真对数收益率序列的描述性统计

由表1可知，仿真和真实对数收益率序列均表现出负偏态和尖峰特征，具有相似的统计分布特征。进一步，利用Mann-Whitney U法对仿真和真实对数收益率的分布是否存在显著性差异进行检验。结果显示，双侧显著性为0.013；因此，在1%的显著性水平下，可以认为仿真和真实对数收益率的分布无显著差异。表1表明，真实和仿真对数收益率序列的分布特征较为吻合。动量生命周期强调动量和反转效应的相互转换，体现的是价格波动趋势。因此，为了对动量生命周期进行研究，需要探究真实和仿真收益率序列在波动趋势方面的吻合性。为此，下文将仿真和真实对数收益率序列的波动趋势利用图形给予展示。在实际画图时，由于序列的数据高达1800个，如果将所有的数据全部罗列，所得到的图形不利于清晰地观察序列在正负之间的转换情况，从而难以分析动量和反转效应的相互转换。因此，为了将波动趋势清晰展现，本文从仿真和真实对数收益率序列中每隔20个数字选择一个数字进行展示，结果见图2。

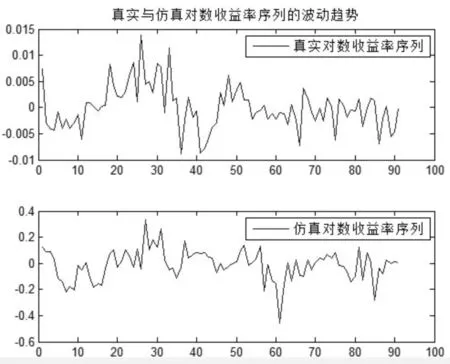
图2 真实与仿真对数收益率序列的波动趋势

由图2可知，仿真与真实对数收益率序列在正负之间的转换较为吻合，即其所刻画动量和反转效应相互转换较为吻合，价格中所体现的动量生命周期现象较为相似。前20期中，对数收益率总体上小于0，即价格在总体上表现出下跌趋势，呈现出价格动量；在20～35期，对数收益率几乎大于0，即价格在20期左右出现反转现象，并再次出现上涨动量；在35期左右，收益率再次变为负值，价格上涨趋势反转，呈现下跌趋势。可见，从首期至35期，对数收益率首先以负值为主，随后由负值转为正值，再由正值转为负值；价格动量和反转趋势随着对数收益率在正负之间的转换而转换。同样地，对35期至末期进行分析，可得到类似结果。仿真收益率在正负值之间转换情况与真实情况的吻合表明，根据FMT所构建的博弈过程进行仿真能较吻合地体现真实价格序列的动量生命周期现象。

综上可见，基于FMT所构建的投资者投资过程模型能够对动量和反转效应的相互转换给予解释。在FMT中关于投资者有限理性和对信息敏感程度存在差异的基础上，投资者对信息敏感程度的差异致使其在根据多数派博弈或少数派博弈在动量和反转策略中动态选择。投资者的这些行为特征反映在证券的过度需求上，并引致证券过度需求在正负之间转换，进而致使动量和反转效应相互转换，证券价格表现出动量生命周期现象。

四、结论与展望

尽管动量生命周期广泛存在于证券市场的事实已被众多学者所认可，但如何对动量生命周期进行理论解释却鲜为人知。本文以近年来日益受到学者们接受的分形市场理论(FMT)为基础，对投资者在动量和反转策略中的动态选择进行设定，并结合少数派和多数派博弈过程，对动量生命周期进行了理论和仿真分析。理论分析结果表明，基于FMT设定的投资者动态选择将致使证券过度需求在正负之间转换，过度需求的转换导致动量和反转效应相互转换，表现出动量生命周期现象。基于上海证券交易所的行业指数日收盘价的仿真分析发现，根据理论模型所生成的仿真对数收益率序列与真实情况较为吻合，基于FMT的投资者投资过程能够解释动量生命周期现象。

本文的研究深化了动量生命周期现象的相关研究，也是对FMT应用的创新。然而，本文的研究属于尝试性探讨，仍存在一些不足。一是本文所构建的模型求解困难，难以直接计算出价格的趋势变化。二是在仿真分析过程中，本文定量分析仍显欠缺；且基于便利，未曾重视不同投资者在记忆长度为hi（t）等参数方面的多样性。对这些缺陷进行弥补是未来重点研究内容之一。

[1]Bernstein R.The Earning Expectation Life Cycle[J].Financial Analysts journal,1993,49(2):90～93.

[2]DeBondt WFM,Thaler R.Doesthe Stock Market Overreact?[J].Journal of Finance,1985,40（3）:793～805.

[3]Jegadeesh N,Titman S.Returns to Buying Winners and Selling Losers:Implications for Stock Market Efficiency[J].Journal of Finance,1993,48(1):65～91.

[4]Lee C,Swaminathan B.Price Momentum and Trading Volume[J].The Journal of Finance,2000,55(5):2017～2069.

[5]Ding D K,et al.Behavioral Explanations of Trading Volume and Short-Horizon Price Patterns:An Analysis of Seven Asia-Pacific Markets[J].Pacific-Basin Finance Journal,2008,16(3):183～203.

[6]Asness CS,et al.Value and Momentum Everywhere[J].The Journal of Finance,2013,68(3):929～985.

[7]Moskowitz T J,et al.Time Series Momentum[J].Journal of Financial Economics,2012,104(2):228～250.

[8]Andrei D,Cujean J.Information Percolation,Momentum,and Reversal[R].NCCRWorkingpaper,2014.

[9]宋光辉，吴栩，董艳.反转和动量效应的国外研究动态及展望[J].金融理论与实践,2014,36(2):94～96.

[10]Franck A,et al.Momentum strategies of German mutual funds[J].Financial Markets and Portfolio Management,2013,27(3):307～332.

[11]Ahmed W M A.The Trading Patterns and Performance of Individual vis-à-vis Institutional Investors in The Qatar Exchange[J].Review of Accounting and Finance,2014,13(1):24～42.

[12]Peters E E.Fractal Market Analysis:Applying Chaos Theory to Investment and Economics[M].New York:John Wiley&Sons Inc.,1994.

[13]Zunino L,et al.A Multifractal Approach for Stock Marke Inefficiency[J].Physica A,2008,387(26):6558～6566.

[14]宋光辉，吴栩，许林.夏普比率时变特征的多重分形分析[J].金融经济学研究,2013,28(5):109～118.

[15]Andersen J V,Didier S.The$-game[J].The European Physical Journal B,2003,31(1):141～145.

[16]刘兴华,杨建梅.多样性和归纳推理与证券市场动力机制[J].系统工程理论与实践,2007,27(5):35～41.