关于点、直线的对称问题

牟建英

（甘肃省礼县职业中等专业学校甘肃礼县742200）

关于点、直线的对称问题

牟建英

（甘肃省礼县职业中等专业学校甘肃礼县742200）

几何图形的对称是美观的，又是基本的、常见的、重要的。下面是解析几何中点与直线的四种对称问题及其解法。

关于点直线对称

一、点关于点的对称

若求点A关于点B的对称点C，即可根据点B是A、C两点的中点，利用中点坐标公式求出。

例1求出点A（1，3）关于点B（-3，2）的对称点C

解设点A关于点B的对称点为C（x0，y0），由中点坐标公式，得

故对称点C的坐标为（-7，1）

二、点关于直线的对称

求点关于直线的对称点的坐标时，用垂直、平分两条件列方程组求解较简单。

设点P1（x1，y1）关于直线l：Ax+By+C=0的对称点为P2（x2，y2），P1P2的中点P0（x0，y0），根据中点坐标公式可用x，y表示x0，y0，又P0在直线l上，可得到关于x，y的一个方程，再根据直线P1P2的斜率与直线l的斜率存在互为负倒数关系，得到另一个方程，联立方程组可以求出P2坐标。

由此可得P2坐标。

例2已知直线l：3x-y+3=0，求点P（4，5）关于直线l的对称点。

解设点P（4，5）关于直线l的对称点为P′（x′，y′），则PP′⊥l且PP′的中点在直线l上。

故P′（-2，7）为所求的点。

三、直线关于点的对称

（1）设动点，运用“轨迹法”求解。

设直线Ax+By+C=0上的任意一点P1（x1，y1）关于点P0（x0，y0）的对称点为P2（x2，y2），则由中点坐标公式可得出x2，y2与x1，y1的关系式，进而用x2，y2表示出x1，y1，再将x1，y1代入直线Ax+By+C=0，即可得P2所在直线方程。

（2）利用线线平行及点到两直线距离相等求解。

例3求直线l1：2x-y+1=0关于点P（2，1）的对称直线l2的方程。

解法1设直线l2上任意一点为P1（x1，y1），则它关于P（2，1）的对称点为P2（x2，y2）。

从而有P2的坐标为（4-x1，2-y1）

又因P2在直线l1：2x-y+1=0上，可得2（4-x1）-（2-y1）+1=0

化简可得l2：2x-y-7=0

解法2因l1与l2关于点P（2，1）对称，所以l1∥l2故设直线l2的方程为：

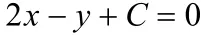
解得C=-7或C=-1（舍去）

故所求的直线l1的方程为：2x-y-7=0

四、直线关于直线的对称

直线关于直线的对称有以下三种解法，都运用了几何性质。

1.利用P与P′是一对“相关点”的性质求出动点的轨迹，这是求曲线关于关于直线对称方程的常用方法。

若求直线l1关于直线l2对称的直线方程l，先设出l1上任一点P（x0，y0），点P关于l2的对称点Q（x，y），再由PQ中点在l2上得到关于x，y的一个方程，由PQ斜率与l2斜率互为负倒数得到第二个方程，联立方程组，解出x0，y0代入直线l1方程，整理可得直线l方程。

2.利用转化求解，即线关于线对称转化为点关于线对称。

3.利用点到直线的距离求解，

例4求直线l1：x-y-2=0关于直线l：x+2y=1=0对称的直线l2的方程。

解法1设直线l2上的动点P（x，y）关于直线l的对称点P′（x′，y′）

因点P′（x′，y′）在直线l1上

化简得直线l2的方程为：7x-y-8=0

解法2在直线l1上取一点（2，0），运用例2介绍的方法，可求得关于l的对称点

直线l2过点P′与Q，有两点式并化简可得直线l2的方程为：7x-y-8=0

解法3先求出直线l1与l2的交点Q（1，-1），再设直线l2的方程为：

y+1=k（x-1）即kx-y-1=0

由对称关系可知直线l上的点到直线l1与l2的距离相等解得k=7或k=1（舍去）

故所求直线l2的方程为：7x-y-8=0

总之，以上主要讲解了点关于点对称、点关于直线对称、直线关于点对称、直线关于直线对称的问题。而点关于点、点关于直线的对称是最基本的对称问题，是解决其它对称问题的基础。