考虑风险阈值的物流基础设施网络布局模型
李汉卿,姜彩良,华 光,闻克宇(.交通运输部科学研究院,北京 0009;.铁道部经济规划研究院,北京 00038)
考虑风险阈值的物流基础设施网络布局模型
李汉卿1,姜彩良1,华光1,闻克宇2
(1.交通运输部科学研究院,北京 100029;2.铁道部经济规划研究院,北京 100038)
在将类似问题总结为考虑风险阈值的物流基础设施网络布局模型(Logistics Infrastructure Network Model under the Risk Threshold:LINM-RT)的基础上,把物流网络上的设施分为两种:“不可靠物流设施”和“可靠物流设施”。模型考虑了设施的最优数量和布局方案,研究拟通过各个设施对消费者需求的配送情况和设施类型的不同给出不同设施的布局方案,分析中断风险概率和消费者的需求对布局产生的影响和表现。分析了在已知条件充足的情况下,如何将LINM-RT模型简化为经典的无设施容量限制设施布局问题模型,并用拉格朗日松弛算法快速地去求解LINM-RT模型。研究结果证明了风险阈值的存在,用算例进一步说明在不同风险概率下物流基础设施网络布局选择是不同的。
风险阈值;供应链风险;物流网络;拉格朗日算法;布局
0 引言
国内外的学者们对于物流网络布局都做了大量的研究。其中,国外学者对于离散布局问题的研究已由传统的问题转为可靠物流设施网络布局问题,其中应急物流系统是其重要的应用领域。Daskin(1982)[1],Ball和Lin等(1993)[2]的研究集中于当中断事件发生时,最大化期望需求的服务范围。Drezner(2006)[3]的研究集中于通过最小化运输成本的权重解决p中值问题(pMP)。本研究基于UFLP问题[4-5](无容量限制的布局问题)提出了考虑风险阈值的物流基础设施网络布局模型(Logis⁃tics Infrastructure Network Model under the Risk Threshold:LINM-RT),模型布局的目标是使物流基础设施固定成本和运输成本最小化。Snyder和Daskin(2006)[6]和Spdhi[7]也在UFLP问题的基础上提出了可靠物流设施布局问题,他们使用混合整数规划将运营成本和期望损失成本之间的关系推导了出来。他们的研究提出了随机鲁棒性模型将概率p考虑了进去,分析了不同风险概率下使总成本最小化的情况。不同于其他研究的是,本研究考虑了可靠物流设施和不可靠物流设施混合的情况,而不是一味地加固为可靠物流设施。其次本研究通过公式推导证明了在一定情况下,中断风险发生概率不同,其供应链布局策略不同,即中断风险阈值是存在的。
陈剑(2001)[8]和张菊亮(2008)[9]讨论分析了一些典型的混合整数规划模型和其考虑的约束条件,提出了供应链模型优化的框架和未来的研究趋势。李彬(2013)[10]、龙静(2014)[11]研究了静态环境和需求不确定环境下的供应链系统节点设施布局和容量的一体化决策问题,建立相应的数学模型使固定成本和运营成本最小,并提出求解用的Benders分解算法。分析了不同阶段客户需求分布和设施运营成本之间的关系,建立了设施布局的评价指标体系。
本研究给出的供应链风险阈值定义为在中断风险下的物流网络结构存在一个风险概率数值或范围,超过了这个数值或范围,物流网络布局最优化设计策略将发生改变。研究将用公式推导来证明在本研究谈论的问题中风险概率阈值是存在的,并通过随机生成的风险概率来模拟不确定的供应链风险场景,从而进一步将阈值明确为具体数值或相对准确的范围,并研究风险阈值和物流网络结构之间的关系,并从物流网络设施布局和需求分配的角度来试着减少企业在面临中断风险时的损失。
研究中断风险下的物流基础设施布局和需求分配。物流基础设施布局问题已经被国内外很多学者研究,并且已经应用到政府或企业的实践中。但是经典的设施布局问题隐含性地假设了所有设施都不会出问题,而且是值得信赖的(reliable)。在此假设条件下建立设施布局的优化布局模型是理想化的。本研究在随机的中断风险下设计了一种具有防御风险的鲁棒性物流网络模型。这里,不是所有的设施都假设是值得信赖的。本研究把供应链上的设施分为两种:“不可靠物流设施”和“可靠物流设施”。“不可靠物流设施”在这里受随机中断风险的影响,它是不值得完全信赖的,会出现中断的情况。“可靠物流设施”是带防御中断风险机制的设施,它需要投入更多的钱去建设,本研究在这里假设这样的设施是值得信赖的。
本研究将类似问题总结为中断风险下的考虑风险阈值的物流基础设施网络布局模型(Logistics In⁃frastructure Network Model under the Risk Thresh⁃old:LINM-RT)。该问题的研究将通过建立混合整数规划模型并用拉格朗日松弛算法来解决。
1 模型建立
考虑风险阈值的物流基础设施网络布局模型(Logistics Infrastructure Network Model under the Risk Threshold:LINM-RT)是在随机不确定的供应链中断风险下,力求达到减少风险事件对供应链布局产生影响的优化设计问题。LINM-RT的目标是使供应链上的物流基础设施因为中断事件而造成的维修成本和预期的运输成本最小化。
1.1基本假设
本研究假设供应链上N表示所有节点的节点集,j是其中的一个节点,且 j∈N,它既可以是消费者需求点又可以是物流设施建设的备选点。在每个节点上,本研究可以建造一个“不可靠设施”,成本为∫Uj,发生中断事件的概率是qj(0
1.2模型参数说明(见表1)
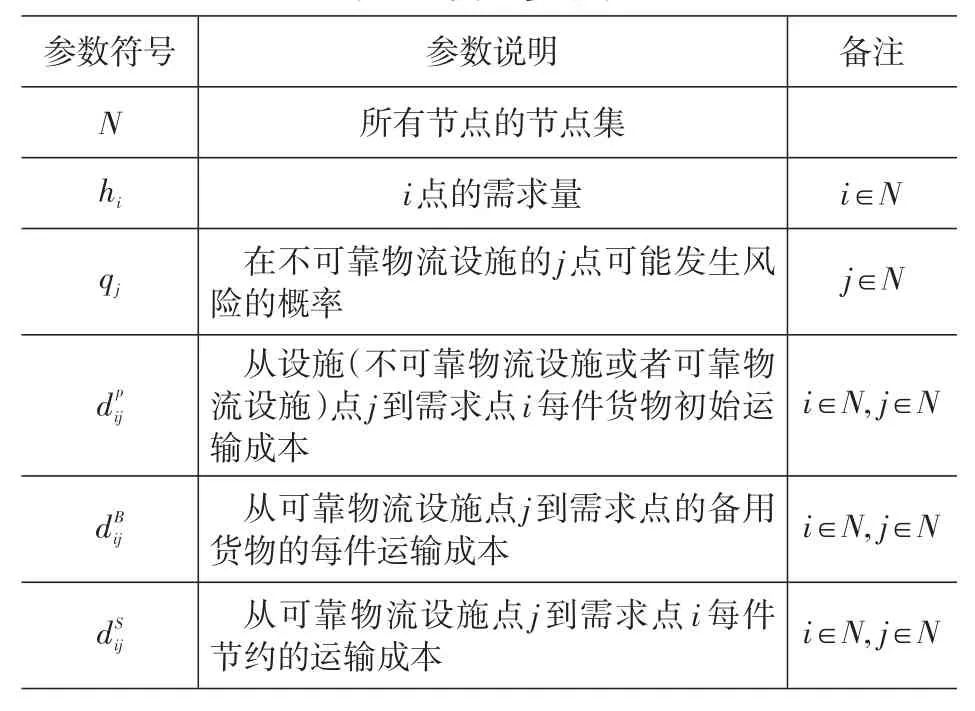
表1 模型参数表
1.3决策变量(见表2)

表2 模型决策变量表
2 网络模型设计
2.1目标函数
根据上面的假设和各种参数和变量的设定,本研究建模如下:模型(1)包含五个部分。前两个部分是建造
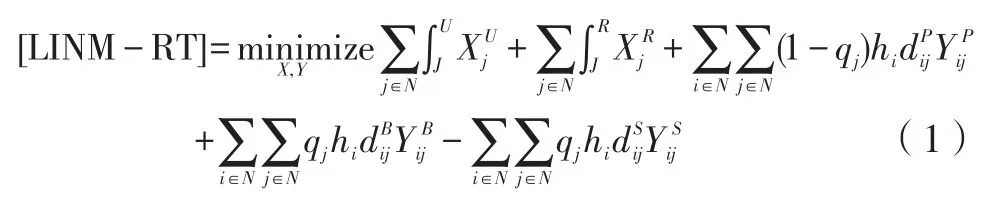
不可靠物流设施和可靠物流设施的固定成本。第三部分表示当初始发货可以满足需求时的运输成本(初始发货的点可能是不可靠物流设施或可靠物流设施)。第四部分表示当需要备用货物来满足需求时的运输成本。第五部分为当一个可靠物流设施点既为其中的需求点进行初始发货又为受不可靠物流设施影响的需求点发送备用货物时节约的运输成本。
2.2约束条件
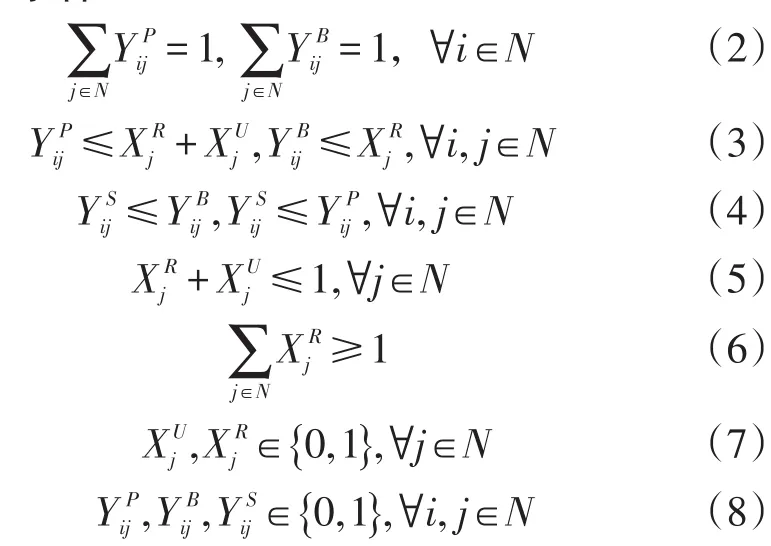
约束(2)供应链上的物流设施会对每一个需求点进行服务,有的是初始配送满足的需求,有的是备用货物满足的需求。约束(3)表示初始配送一定是一个已设立的物流设施完成的,而备用货物的配送一定是可靠物流设施完成的。约束(4)说明任何配送所节约的成本都仅被认为是当一个可靠物流设施点既为其中的需求点进行初始发货又为受不可靠物流设施影响的需求点发送备用货物时节约的运输成本。约束(5)表示为避免不必要的浪费,本研究不能在同一点上既建立可靠物流设施又建立不可靠物流设施。约束(6)说明在供应链设施建设中,本研究至少建立一个可靠物流设施来抵御可能发生的风险,给受中断事件影响的需求点配送备用货物。约束(7)和(8)是整数规划的约束。
2.3改进的算法
LINM-RT模型可以使用CPLEX这样的优化软件进行计算,但是计算时间和空间资源消耗随着数据规模的增加而加大。由此考虑,本研究设计了一个基于拉格朗日松弛定理(LR)的算法。
本研究加入拉格朗日乘数l和μ使约束条件(2)松弛,则目标函数变为:
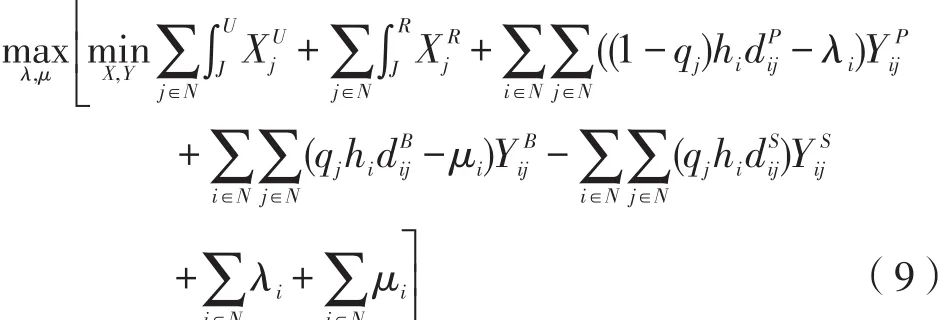
约束条件依旧为式(3)~式(8)。
本研究试着用X和Y将目标函数最小化,用λ 和μ使函数最大化。目标函数(1)进一步可以被改写为:
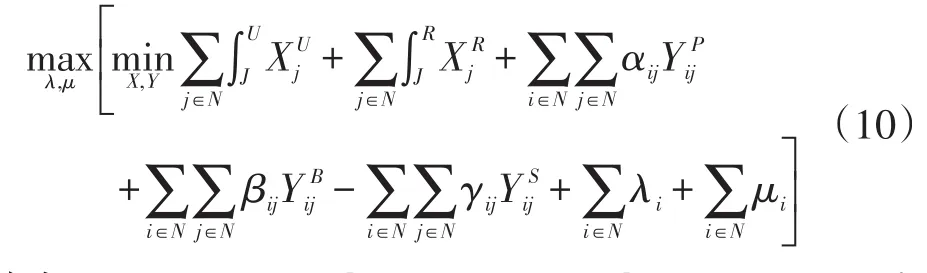
其中:αij=(1-qj)hi-λi,βij=qjhi-μi,γij=qjhi
如果(10)中拉格朗日乘数λ和μ取固定值,它会为目标函数(1)提供了一个下限。本文用如下步骤处理(10)。
步骤1:判断不可靠设施在j点的值(例如,使XjU=1)。如果αij=(1-qj)hi-λi<0,本文可以设YiPj=1。因此,如果=1,那么独有的固定设施成本为=∑i∈Nmin(0,αij)=∑i∈Nmin(0,(1-qj)hi-λi)。
ij
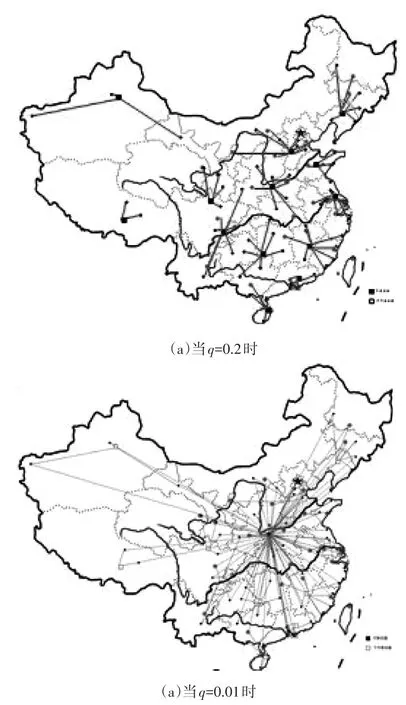
步骤4:在设置完选址变量后,本文得出∑j∈N≥1,计算下限的问题由选址变量来决定。如果∑j∈N=0,本文需要修改下面的选址决策,让N1={j|
=1},并且N0={j|=1}。现在本文设V1=minj∈N{+-(+)},并且 j1= arg minj∈N1{+-(+)}。相似地,设V0= minj∈No{+},并且 j0=arg minj∈N0{}。最终,本文设:如果V1 一旦知道了选址决策变量的值,只需根据上述关系简单地进行计算。计算上限步骤同计算上限步骤。 初始化:本研究初始化拉格朗日乘数λ和μ,得: 改进:国外学者Daskin(1995)都用标准梯度优化对拉格朗日乘数每次迭代进行改进。下面就是改进后的迭代公式: dλi( n)和diμ(n)代表在第nth次迭代后λ和μ分别的方向,此时迭代步骤的规模为t(n)。特别地, 步骤0:本研究先计算了在第nth次迭代后的改进方向: C是克罗德阻尼常数(Crowder damping con⁃stant)。本研究设C=0.3,==0(∀i)。 步骤1:本研究接下来计算迭代步长(step size)t(n): α(n)是在第n次迭代下的常数,初始值为2.0,并当24次连续迭代失败后减半到达下限值。UB代表通过第n次迭代的上限值。ζ(n)代表第n次迭代的下限值。 步骤2:最终,本研究改进了式(11)中的λ 和μ。 在这一小节,将LINM-RT模型进行深入分析。通过推导证明发现在中断风险发生概率达到极值时,模型可以转换为UFLP(Uncapacitated Fixed Charge Location Problem)问题,即无固定容量限制的布局问题。最终,发现了在一些情况下,中断风险概率存在阈值。 定理1.在LINM-RT模型中存在一个中断风险事件发生的概率阈值qˉth(<1),如果qj≥qˉth,最优方案是仅建立理论上能抵御中断风险事件的可靠物流设施。此时,模型最优化布局正好与UFLP问题的布局一样,设施成本为,距离为。 证明:上述模型的参数说明中已经提到q是中断风险发生的概率。本研究可以假设一种情况S:(XU,XR,YP,YB,YS),其中包含至少一处不可靠物流设施,变量XU,XR和YP,YB,YS分别代表优化后的布局位置和配送方案。本研究再假设另一种情况:(0,XR,YB,YB,YB)。 ZSCRDP(S)是在S情况下LINM-RT问题的总成本。因为≥,并且,所以无论q取何值,都有: j∈N满足: 设ZUFLP(XR,YB)是UFLP的总成本,设施成本为,距离为。XR,YB是布局分配变量。这等同于ZSCRDP(0,XR,YB,YB,YB)。即: ZSCRDP(XU,XR,YP,YB,YS)≥ZSCRDP(0,XR,YB,YB,YB) X*,Y*是UFLP的最优解,此时设施成本为,距离为。所以在LINM-RT模型中存在一个中断风险发生阈值qˉth(<1),如果qj≥qˉth,此时式(12)说明了模型最优化布局正好与UFLP问题的布局一样,设施成本为,距离为(证明结束)。 推论1.中断风险概率阈值qˉth范围为 综上定理1和推论1,当中断风险概率大于阈值时(qj≥qˉth),最优方案是将所有设施都变为带有防御机制的可靠物流设施。一旦加固了所有的节点设施,LINM-RT模型中的网络将成为一个理论上“无风险”(risk free)的环境,这类问题也就可以直接转化为UFLP问题来求解最优化方案。 下面,本研究考虑当中断风险概率很小时的情况。 证明:考虑一个可行的方案: (XU,XR,Yp, YB,YS),其中包括了至少两个能抵御中断事件的可靠物流设施。可以概括为∑j∈N=k(≥2)。还可以考虑另一个可行的方案,把S其中所有的可靠物流设施转换成不可靠物流设施,只留下一个。(因为LINM-RT中可靠物流设施最少的数量是1个。)更精确地,设S͂:(X͂U,X͂R,Y͂p,Y͂B,Y͂S),则有如下: 对于任意中断风险概率q,本研究都可以得出: 因为δ>0,可以找到一个概率q满足ZSCRDP(XU,XR,YP,YB,YS)≥ZSCRDP(X͂U,X͂R,Y͂P,Y͂B,Y͂S),趋近于0。即在给定的S中,如果qj<,总存在一个风险阈值,此时最优化方案是精确地加固一个设施是其为理论上能抵御中断事件的可靠物流设施。 接下来本研究考虑UFLP问题,把总成本设为ZUFLP(Xˉ,Yˉ),其中设施成本为,距离为,=͂+,Yˉ=͂。可以找到一个中断风险概率q,则: 本研究可以通过求解赋权重心问题(1-medi⁃an location problem)来确定哪个设施需要被加固成为理论上能抵御中断事件的可靠物流设施。因为设施加固费用是个常数,从正在运营的设施中找到一个设施进行加固,要保证在中断风险发生时总运输成本最小。设N′为一个包括所有定理2中的节点的集合,本研究推出如下推论。 推论2:在定理2中的UFLP选择一个设施进行加固的问题可以运用有如下赋权重心法来确定: 约束条件: 本文模拟场景为大型企业在遇到中断事件时,全国范围内供应链选址策略的调整方案。数据选择了中国263个大城市作为模型中的节点。中断风险概率qj被假定为独立事件,且是随机的,范围被设为U~[0.01,0.2]之间。不可靠设施成本由固定成本和由该地区人口多少决定的可变成本决定。例如:=500000+1.7hj。每个节点的加固成本由中断风险发生概率的线性函数决定。例如,δj=-=5000000qj,这样的城市发生中断风险概率越高就要花费更多去加固节点。在假设中,本文把加固成本定为不可靠设施固定成本的25%。任意两城市之间的距离按照经纬度来计算。本文设c=0.002为每一件货物运送的单位距离成本。备货运输成本为=。算法用C++编码,用IBM workstation进行计算(2.4GHz,双核处理器,8GB内存)。在运行12s进行265次迭代后,最优化的拟合误差在0.0008%(上限和下限值差的平均值)。方案中有12个不可靠设施和10个可靠设施(不可靠设施:鞍山,德惠,张家口,淄博,连云港,咸阳,绵阳,怀化,九江,金华,湛江,惠州;可靠设施:沈阳,石家庄,常州,运城,宜宾,拉萨,乌鲁木齐,海口,赣州,东莞)。初始既为可靠设施的点只被指派1次,初始为不可靠设施的点被指派2次。目标函数最终计算成本为45 878 459元。本文也通过改变中断风险概率的方式验证了定理1和2。图1(a)是当中断风险大时的计算结果(验证定理1),图1(b)是当中断风险q小时的结果(验证定理2)。本文分别设q=0.2和0.01,其他变量都无变化。通过两个例子的比较,可以发现可靠设施的建设数量由中断风险概率q来决定。 图1 定理验证计算结果 本研究通过建立混合整数规划模型并用拉格朗日松弛算法对其进行求解。在模型中,本研究考虑了设施的最优数量和布局方案,并且考虑了各个物流设施对消费者需求的配送情况。结论如下: (1)建立LINM-RT模型并求解,研究设施的布局方案和不同类型设施之间的关系,分析中断风险概率和消费者的需求对布局产生的影响和表现。 (2)本研究分析了在已知条件充足的情况下,如何将LINM-RT模型简化为经典的UFLP设施布局问题模型。 (3)本研究用拉格朗日松弛算法快速地去求解LINM-RT模型,并证明风险阈值的存在。 (4)本研究通过算例来模拟中断风险物流基础设施的布局方案。 [1]Daskin M S.Application of an Expected Covering Model to Emergency Medical Service System Design[J].Decision Sci⁃ence,1982,13(3):416-439. [2]Ball M O,F L Lin.A Reliability Model Applied to Emergen⁃ cy Service Vehicle Location[J].Operations Research,1993, 41(1):18-36. [3]Drezner Z,Marcoulides G A.Mapping the Convergence of Genetic Algorithms[J].Journal of Applied Mathematics and Decision Sciences,2006(4):1-16. [4]Fisher M L.The Lagrangian Relaxation Method for Solving Integer Programming Problems.Management Science,1981, 27(1):1-18. [5]Fisher M L.An Applications Oriented Guide to Lagrangian Relaxation[J].Interfaces,1985,15(2):10-21. [6]Snyder L V,M S Daskin.Stochastic P-Robust location Problems[J].IIE Transactions 2006,38(11):971-985. [7]MMS Sodhi,BG Son,CS Tang.Researchers′Perspectives on Supply Chain Risk Management[J].Production and Opera⁃tions Management,2012,21(1):1-13. [8]陈剑,蔡连侨.供应链建模与优化[J].系统工程理论与实践,2001(6):26-33. [9]张菊亮,陈剑.供应商管理库存应对突发事件[J].中国管理科学,2008,16(5):71-77. [10]李彬,季建华.综合收益和风险的供应链鲁棒性指标模型研究[J].上海交通大学学报,2013(3):484-488. [11]龙静,张以彬,陈俊芳.制造供应链风险的虚拟应急管理研究[J].现代管理科学,2014(8):70. Logistics Infrastructure Network Model under Risk Threshold LI Han-qing1,JIANG Cai-liang1,HUA Guang1,WEN Ke-yu2 Related to the application of operations research and theoretical studies,a model of logistics infrastructure network design under risk threshold(Logistics Infrastructure Network Model under the Risk Threshold:LINM-RT)was proposed.The facilities on the logistics network were divided into two types"unreliable logistics facilities"and"reliable logistics facilities".Different facility layout plans were proposed through distribution of various facilities for consumer demand and different types of facili⁃ty.The impact and performance of disruption risk probability and consumer′s demand generated on site were analyzed.How to reduce LINM-RT model to the classic non-facility capacity constraints facility problem model and use Lagrangian to solve LINM-RT model quickly were analyzed.The results prove the existence of the risk threshold.With examples,it is illustrated that options of logistics infrastructure network layout under different probabilities of risk are different. risk threshold;supply chain risk;logistics network;lagrangian algorithm;layout F287.3 A 2095-9931(2015)01-0106-08 10.16503/j.cnki.2095-9931.2015.01.018 第1卷 第1期|2015年2月 2014-12-30
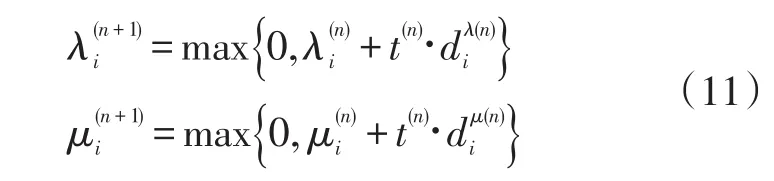
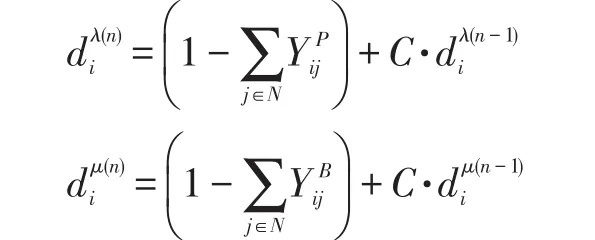
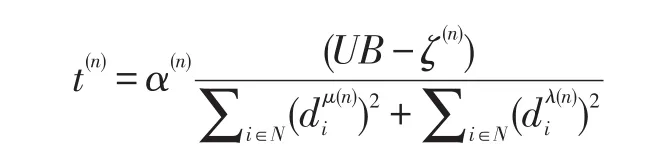
3 中断风险阈值研究
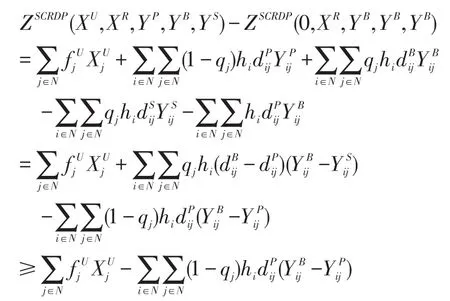
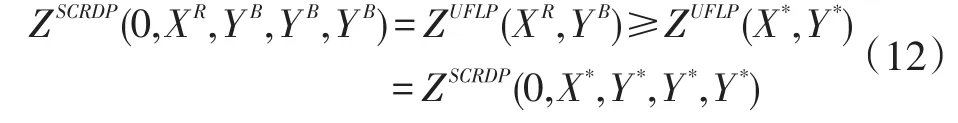

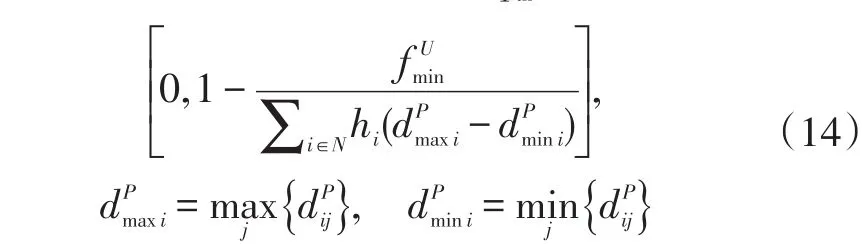

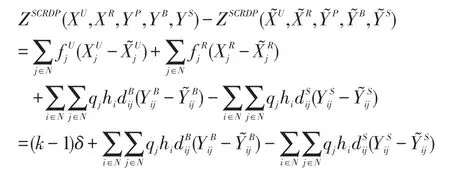
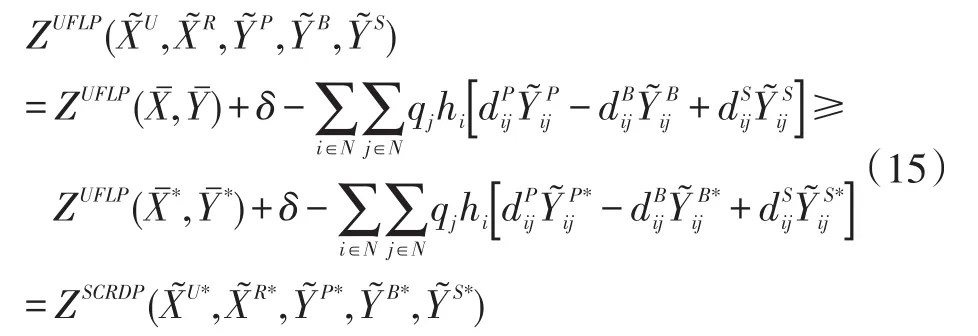
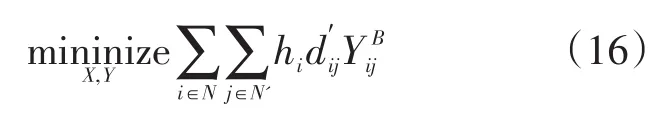
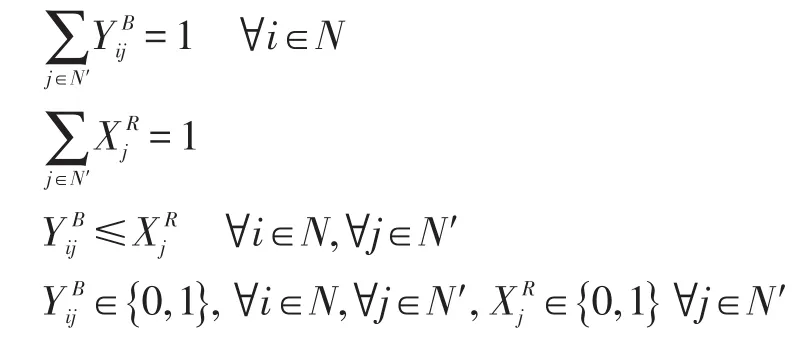

4 算例分析
5 结论
(1.China Academy of Transportation Sciences,Beijing 100029,China;2.Economic and Planning Research Institute,Ministry of Railway,Beijing 100038,China)

