基于智能优化算法的动态路径诱导方法研究进展

游　尧，林培群（华南理工大学土木与交通学院，广东 广州 510640）

基于智能优化算法的动态路径诱导方法研究进展

游尧，林培群
（华南理工大学土木与交通学院，广东 广州 510640）

采用综述的方法对当前动态路径诱导方法中一些有代表性的智能优化算法进行了深刻的探讨与总结,为未来进行深入而广泛的智能交通系统研究及应用奠定基础。主要从算法特性、改进效果、性能评价等方面详细讨论了智能优化算法在动态路径诱导系统中的常见改进机制及其效果，给出了这些优化算法的基本思想、优缺点及其应用局限性；并对智能优化算法性能评价方法的研究现状进行了详细的分析与总结，为建模人员和研究人员对智能交通系统中动态路径诱导方法的选择和研究提供支持；最后结合算法应用分析成果，展望了智能优化算法在动态路径诱导系统中的应用发展前景和智能交通系统中进一步研究未来动态路径诱导算法的重要研究方向。

动态路径诱导方法；研究进展；智能优化算法；蚁群算法；遗传算法

第1卷 第1期|2015年2月

0　引言

面对规模越来越大的城市交通网络，路径寻优的效率问题使得基于纯数学理论的最优路径算法面临新的挑战。传统的图论方法（如Dijkstra算法）和数学规划方法计算量大，以致计算时间长；而且根据几何距离、道路质量为路阻计算最优路径，不能客观描述现实交通网络的时变性。文献[1]指出，路径诱导是一个对实时性要求相当高的系统，过分追求模型的精确和复杂并没有多大帮助。描述交通网络的模型越复杂，算法的灵敏性就会减弱，最优路径的求解复杂度也越大，计算中的省略误差通常也越大，这些都会降低模型精确带来的优势。近年来，一些学者采用对模型精度要求较低的智能化方法研究动态交通诱导问题，智能优化算法[2-3]放宽了优化问题目标函数，加之本身的灵活性，在解决复杂结构优化问题方面有着传统优化算法无法比拟的优越性。因此，智能优化算法在各个领域的优化计算中都得到广泛的应用，依赖这类算法，理论上可以在尽可能短的时间内找到问题的最优解或近似最优解。

1　动态路径诱导方法研究现状

基本智能优化算法缺乏坚实的理论基础，同时，其效率低、容易陷入局部最优等缺陷，难以满足动态路径诱导的实际需要。因此，在应用领域的研究也多是采用实验的方法，针对特殊的问题，设计特殊的优化算子，通过反复实验来确定算法参数，其设计步骤如图1所示。通过优化设计而形成的方法在精度、精度时间比等评价指标[4]上往往能取得满意的效果。

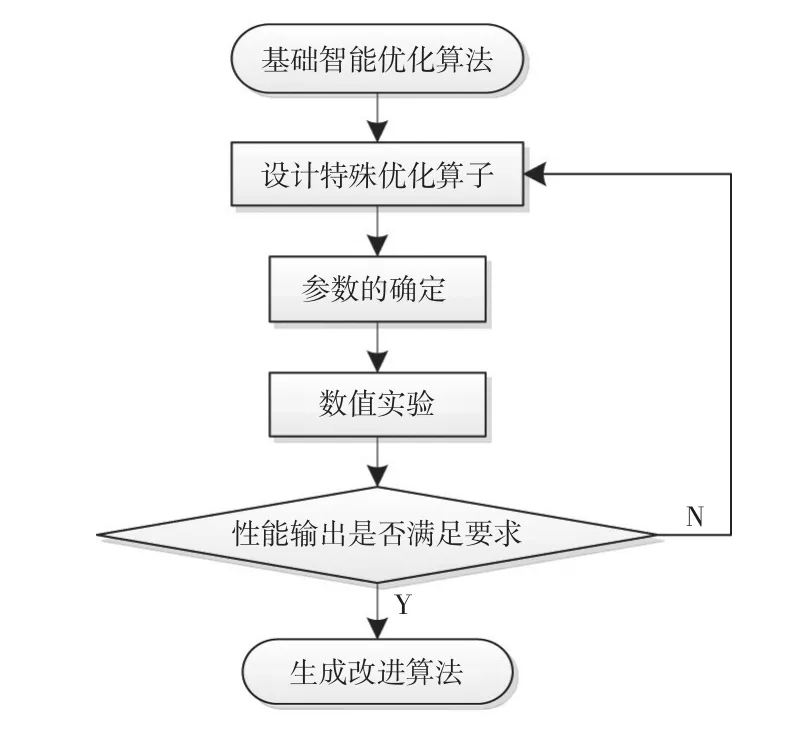
图1　基于智能优化算法的动态路径诱导方法设计步骤

数值实验是验证算法的重要方法，选取合适的测试样本是数值实验的关键。实验的内容就是算法的整体性能评价、算子测试以及参数测试。数值实验的结果一般反馈到参数选取阶段，通过参数的相关性和灵敏度测试，可以大致地确定参数变化对算法运行的影响。经过实验，发现一些能够取得较好运行效果的参数，如若达不到预期还可以优化算子设计。

1.1基于蚁群算法的动态交通诱导方法

蚁群算法[5]是受自然界蚂蚁寻路行为启发产生的一种具有自适应特性的模拟仿生算法，不需要建立复杂的数学模型和大量数学计算，简单易实现。蚁群算法自问世以来表现出了强大的生命力，具有并行性、正反馈性、健壮性等特点，且搜索过程不需要人工干预，在求解旅行商（TSP）问题、分配问题、job-shop调度问题上都取得了较好的效果[6-9]。基本蚁群算法在其开始时，信息素的作用不明显；虽然过程中正反馈机制能强化得到较好解，但却使算法出现停滞现象，即只取得了局部最优解就停止，而未达到全局最优解。因此，学者对其进行了一系列改进研究以适应动态交通网络实时性与快速性的特点。

杜长海、黄席樾等人[10]提出带方向的信息素更新和混沌选择策略来改进蚁群算法，算法将路网节点间的相对位置信息引入信息素更新，以加快搜索速度；使用混沌扰动改进选择策略，以避免出现早熟停滞现象。其优点在于通过对自然界中蚂蚁寻路行为的模拟，在全局范围内动态确定车辆最优行驶路线，提高了整个交通系统的效率。

Yang[11]结合实时的城市道路交通流信息来解决城市动态路径诱导难题，提出了一种基于蚁群优化的算法，为司机提供实时最佳路径。算法使用优先级高的干线道路循环和实时交通信息，减少并避免驾驶困难的道路；考虑到具体城市交通的特点，采用限制搜索区域机制来减少蚂蚁的时间复杂度，提高了算法的搜索性能。

周明秀、程科等人[12]提出了动态路径规划中改进蚁群算法的方法，算法改进距离启发因子以增加目标节点对下一节点的影响，从而提高全局搜索能力，避免陷于局部最优解，提高收敛速度；引入多个路径质量约束来改进信息素更新，模拟出行者在选择路径时表现的多目标性及各目标属性的特点。算法保证了在较短时间内得到全局最优解，有效地克服了传统蚁群算法中收敛速度慢、易陷入局部最优解的缺陷。

党希望[13]提出基于主次种群策略的蚁群算法的动态路径优化算法，相应的加入了信息素交流机制和信息素更新方法，并根据动态路网模型和TSP模型的不同，适时改进了路径交叉变异策略和路径去交叉策略；将小窗口策略和PASPAS算法中状态转移参数的归一化处理结合起来，减少了数据处理量，增加了状态转移概率的准确性。算法结合路径交叉变异策略和路径去交叉策略的优势，虽然时间复杂度略有提升，但解质量和搜索能力得到了改善。

刘伟[14]给出了一种基于信息素扩散策略的双种群蚁群算法——PDDPAS算法。算法选取了三个不同规模的TSP问题对PDDPAS算法进行实验，分别对PDDPAS算法性能、参数的设置、信息素扩散的策略进行考察，得出了相应的设置方案。PDDPAS算法使用信息素扩散策略提高了算法的全局寻优能力，使用双种群策略提高了算法的收敛速度。

董永峰、刘艳柳等人[15]提出了一种基于改进蚁群算法的求解K最短路径方法，实现了动态路径诱导系统中K最短路径的搜索，通过引入方向函数作为新的启发式因子，使其能在更少的繁殖代数下搜索到全局最优解，提高了算法的全局搜索能力。在求解K最短路径时将交叉口延误时间这一因素加入了目标函数中，使之符合出行者的出行行为。

林娜、霍志胜等人[16]提出基于免疫遗传的多路搜索蚁群动态路径诱导算法，利用了蚁群系统算法的动态性、正反馈性和分布式计算的优点；同时兼容了免疫遗传算法的全局搜索能力以及容易和其他算法相结合等特点。随着动态因素的增加，算法的复杂性也在增加，因此算法的效率在降低，同时算法又易陷入局部最优状态。

HUANG[17]通过在实时交通信息网络中采用蚁群算法找出最优路径，然后利用群决策理论提出了基于蚁群算法和群体决策的动态路径优化方法。算法考虑了相邻交叉口距离以及部分交通流饱和度两个参数，结合蚁群算法和最优路径，通过不同群体决策算法的结果比较得到了最优动态路径优化方法。

总的来说，基于蚁群算法及其改进算法的动态路径诱导研究一直都未停止，研究者尝试各种策略来解决基本蚁群算法的应用缺陷以及探索其能够适合的结合算法。特别是基于蚁群算法的动态路径诱导应用研究已经比较成熟，在适应性、加速收敛、防止早熟停滞、解的多样性与全局性等性能上都得到了较大提高[18]，能满足动态路径诱导需求。

1.2基于遗传算法的动态交通诱导方法

大家公认的遗传算法[19]是建立在自然选择和群众遗传学机理基础上的随机、迭代、进化、广泛适应性的搜索方法，其最先由John Holland于1975年提出，从此以后，它逐渐发展成为一种通过模拟自然进化过程解决最优化问题的计算模型，近年来，基于遗传算法的动态路径诱导方法的应用研究也越来越深入。

杨兆升等人[20]基于从出行点出发，径流量最大的通道到达目的点的路径就是对应于交通网络的最短路径假设提出了一种将交通流比拟成自然流体的神经网络诱导模式，并用遗传算法来优化流体神经网络的参数。计算表明，这种方法较传统K路最短算法优越，并且成功率较高。

Hitoshi等人[21]为实现车辆实时导航，提出了基于遗传算法的动态路径选择方法，研究分析了遗传算法用于动态路径诱导的优势，设计了从当前遗传算法路径解集中产生新路径的方法，对路口交通灯下的等待、换道等行为进行了模拟实现，通过与Dijkstra算法的对比实验，验证了遗传算法的用于动态车辆导航的高效性。但是文中很少涉及遗传算法在动态路径诱导方面的具体算子设计，具有较大的局限性。

张水舰、李永树等人[22]在建立时间依赖的动态交通网络模型的基础上，提出了基于遗传算法GA 和GIS的动态路径诱导算法，设计了基于改进轮盘赌方式的个体选择方式和高效的算子交叉、变异规则，仿真实验表明时间依赖动态交通网络模型适用性较高、算法收敛性良好，在一定程度上消除了动态诱导中的Bracess现象。

遗传算法中的关键是初始种群，初始种群的好坏将直接影响算法的收敛速度和收敛结果。邹亮、徐建闽等人[23]提出了一种以随机Dijkstra最短路径算法为基础，运用遗传算法来求解动态路径诱导系统中最短路径问题的算法，不仅能够较快地求出较优的路径，而且对网络没有任何的约束条件，对离散和连续的动态网络模型都有效。

李松江[24]通过有损算法来减少遗传算法初始种群的规模，从而提升了遗传算法的整体效率；还将模拟退火算法引入到遗传算法中，解决遗传算法过早收敛的缺点。而且考虑到用户的出行习惯，通过对适应度函数的修改，可以使算法更人性化，更符合人机工程。通过实例验证了算法的可行性，较一般的遗传算法和有损算法有着更高的搜索效率和更精确的最优解。

李春元、魏武等人[25]鉴于采用序号编码方式进行遗传操作时会产生大量无效路径，结合城市道路交叉口左转、右转、直行等转向行为，设计了一种新的基于转向行为的编码方式，减少了染色体在交叉、变异时的无效路径的生成。算例表明，这种编码方式可以有效提高算法收敛性，更容易获得最优解。

孙霞[26]通过引入一种新的带染色体交叉控制策略的改进遗传算法，保证了一对适应值有一定差异的染色体进行交叉，使产生的后代性状分离，并配合引入单点交叉算子，可以增加种群中个体的多样性，扩展解的搜索空间，避免了局部极值解；配合单点交叉算子，消除了传统遗传算法中早熟收敛的不足，并使所求最优路径更加贴近实时的交通状态，切实达到诱导目的，提高整体路网的运行效率。

赵丹[27]研究了适用于动态最优路径求解的改进自适应遗传算法，通过引入个体适应度改进算子选择、设置不随适应度改变的遗传率和变异率，解决了局部极小和收敛速度慢的问题。建立城市路网模型和车辆路径模型，把改进的自适应遗传算法应用到动态交通条件下路径诱导的最优求解，仿真比较结果验证了改进自适应遗传算法用于动态最优路径计算、效率和实用性方面的优势。

Mainali等人[28]在分层网络上提出基于遗传算法的高层网络修剪方法，以此提高交通网络计算效率。路网由子网和始发地、目的地与边界路口相交的高级网络构成，在搜索过程中减少高层网络边界路口的数量以提高搜索速度，但同时导致搜索路径精度下降，因此在遗传算法评价函数中引入了搜索时间与优化目标权重参数，以此提高搜索精度。使用道路网进行修剪搜索验证，结果表明，该方法提高了计算效率且准确性丧失较小。

总之，遗传算法作为一种模拟生命进化机制的随机搜索优化方法，以其简单通用、鲁棒性强、适于并行处理以及应用范围广等特点得到了学者的青睐，但其易出现早熟现象以及对初始种群很敏感。为了适用于动态交通网络，研究者在算子设计、初始解选择等方面[29]进行了改进设计，通过仿真实验等手段证明改进算法的合理性与高效性。

1.3基于其他智能优化算法的动态交通诱导方法

遗传算法、蚁群算法在动态路径诱导中的应用研究较为常见，形成了一套比较完整的动态路径诱导应用理论体系。除此之外，神经网络算法[30]、粒子群优化算法[31]的动态路径诱导的应用研究相对较少；禁忌算法[32]、模拟退火算法[33]等算法应用研究目前则主要停留在静态路径规划阶段。

李菲、肖洪祥[34]在动态路径优化中引入了一种神经动态规划算法，解决传统算法计算大规模路网的优化问题时所表现出来的计算时间长、存储空间大等缺陷。它将传统的动态规划和BP神经网络结合起来，通过逼近Q学习算法来寻求一种最优策略，最终达到路径优化的目的。实验表明，该方法的实时性、并行性和全局性都优于传统动态规划。

马艳丽、裴玉龙[35]将混沌神经网络应用于动态路径诱导，在神经网络中引入混沌动态，利用其遍历性进行随机搜索，再由退火策略控制混沌动态逐渐消失并转入HNN进一步优化，从而可保证网络收敛到一个最优或近似最优的稳定平衡点。通过仿真实验验证了将混沌神经网络应用于动态路径诱导系统总能保证网络收敛至全局最优，有效克服了Hopfield神经网络易陷入局部最优解的缺点，具有更高的搜索效率。

吴成东，杨丽英等人[36]提出了将神经网络与遗传算法结合的动态路径诱导方法，研究了基于神经网络的交通信息实时预测方法，构造了具有时变性的路阻矩阵，解决了传统静态路阻存在的时变性差等局限性问题；提出了适用于路径优化的编码方式、适应度函数和遗传操作算子，解决了求解效率和求解质量的平衡问题。

CHEN[37]在分析粒子群优化算法的最基本原理和特征基础上，从算法初始化、译码、健壮性计算、位置与速度更新等多个方面进行分析，针对动态交通网络特点设计具体的改进方法，将粒子群优化算法应用在动态路径诱导中。仿真实验表明，当用于动态路径道路网络搜索时，粒子群优化算法具有速度快、准确性高的特点，因此表明了粒子群优化算法用于动态路径诱导的可行性与高效性。

陈曦[38]在分析常规粒子群优化算法的基础上，针对动态交通问题，采用一种带变异因子的改进的粒子群优化算法。这种免疫粒子群优化算法结合了粒子群优化算法具有的全局寻优能力和免疫系统的免疫信息处理机制，并且实现简单，改善了粒子群优化算法摆脱局部极值点的能力，提高了算法进化过程中的收敛速度和精度，实验表明其提出的算法具有较好的性能。

DENG[39]提出一种基于神经网络模型和粒子群算法相结合的优化方法，算法搜索时使用改进间接路径编码方案，简单、收敛速度快，不易陷入局部最优解；针对不同拓扑交通网络结构进行模拟实验，均能以较高成功率找到最优解和近似最优解。混合算法大大提高了流体神经元网络的收敛效率，同时，神经网络模型和粒子群算法都是并行算法，很容易运行在并行计算机甚至神经计算机上，从而大大减少计算时间。

杨清波[40]采取了一种新的群智能优化算法——人工鱼群算法[41]来实现GIS环境下的动态交通最优路径的求解，针对原始人工鱼群算法初始鱼群覆盖空间的不确定性和收敛速度慢等问题进行了改进研究。采用网格化鱼群，使初始人工鱼群在海域中均匀分布，利于人工鱼更快的在全局范围内寻优；算法中设立一个公告板，用来记录最优人工鱼的状态和该人工鱼位置的食物浓度，以记录历史最优状态。通过实验对算法中各参数的选择进行了研究，得到了较优的参数组合，并验证了改进算法的有效性。

2　算法性能评价研究现状

目前，常见的禁忌搜索算法、模拟退火算法、粒子群优化算法、遗传算法、蚁群算法等常被用来解决各个领域的NP完全问题。智能优化算法对解决组合优化问题都有较好的应用，但随着实际问题的变化，各智能算法都有其不足之处。因此，建立一套符合智能优化算法特点的评价标准对于其改进与应用研究十分必要。传统优化算法的性能指标主要有两个[42]：收敛性和收敛速度，但其基于确定型的搜索算法，并不适合用于智能优化算法的评价。

动态路径诱导算法应用研究当中，主要通过比较算法时间复杂度、收敛速度等传统优化算法评价指标评价算法应用的有效性，也有通过比较找到最优解的概率及其稳定性等模糊性指标，但缺乏完整的评价体系及理论依据。杨劲秋[4]详细分析了传统优化算法的评价标准在智能优化算法评价中的局限性，根据智能优化算法的特点，提出了智能优化算法的一系列具有可操作性的评价指标，并提出了基于随机搜索的性能评价及优化解概率的分阶段估计方法，对智能优化算法的行为及其算子给出了具体的评价方法。

3　结论与展望

动态路径诱导是智能交通系统中最为人们所期许的功能之一，一般应具有通过考虑交通网络的变化来提供最小出行时间路径的功能。本文研究了目前常见智能优化算法在动态路劲诱导中的应用研究情况，为了更好地评价各种智能优化算法在动态交通诱导问题上的应用效果，提出了具有偏好的智能优化算法多指标评价模型。国内外有很多学者都曾对动态交通网络的特点，有针对性地进行算子设计、参数优化等研究工作，但该问题的研究大多停留在假定性较强的理论层次，动态路径诱导算法的实时性仍然还是一个很少有人涉足的研究领域[2]。

智能交通系统中的路径诱导算法是一个复杂的系统工程，具有很强的理论性和实现上的挑战性。随着车联网、移动互联网等技术的发展，结合智能交通系统的实际需求，基于智能优化算法的动态路径诱导算法将会有更广阔的前景，其应用研究可以分为以下三个方向。

（1）应用算法类型的多元化。一方面，随着研究的不断深入以及遗传算法与蚁群算法的应用实践，智能优化算法的优势逐渐表现出来，受到更多研究者和交通部门的重视；另一方面，最优路径搜索问题也属于组合优化问题，智能优化算法在一系列NP问题已经证明了其优越性，而传统算法难以解决规模越来越庞大的动态交通网络寻优问题。

（2）算法之间的结合性发展。单个智能优化算法具有的某些缺点难以满足动态交通网络实际需要，如果采用混合算法，用其他智能优化算法的思想对某种智能优化算法进行改进，往往能取得更好的效果。（3）发展基于多目标优化的智能优化算法。

实际问题中常常需要同时考虑路程最短、时间最少、费用最省、风险最小等多种因素，即节点之间的权重属性有多个。因此研究多目标具有很现实的意义，多目标所得的解是一种“折中”的解。

[1]李威武，王慧.智能交通系统中路径诱导算法研究进展[J].浙江大学学报：工学版，2005，39（6）：819-825.

[2]黄席越，张著洪，胡小兵，等.现代智能算法理论及应用[M].北京：科学出版社，2005.

[3]钟一文.智能优化方法及其应用研究[D].杭州：浙江大学，2005.

[4]杨劲秋.智能优化算法评价模型研究[D].杭州：浙江大学，2011.

[5]Schoonderwoerd R,Holland O,Bruten J,et al.Ant-Based Load Balancing in Telecommunications Networks[J].Adap⁃tive Behavior,1996,5(2):169-207.

[6]Colorni A,Dorigo M,Maniezzo V,et al.Ant System for Job-Shop Scheduling[J].Belgian J of Operations Research Statis⁃tics and Computer Science,1994,34(1):39-53.

[7]Dorigo M,Maniezzo V,Colorni A.Ant System:Optimization by a Colony of Cooperating Agents[J].IEEE Transactions on System,Man,and Cybernetics-Part B,1996,26(1):29-41.

[8]Dorigo M,Gambardella L M.Ant Colony System:A Coopera⁃tive Learning Approach to the Traveling Salesman Problem [J].IEEE Transactions on Evolutionary Computation,1997,1 (1):53-66.

[9]Mohemmed A W,Sahoo N C,Geok T K.Solving Shortest Path Problem Using Particle Swarm Optimization[J].Applied Soft Computing,2008,8(4):1643-1653.

[10]杜长海，黄席樾.改进的蚁群算法在动态路径诱导中的应用研究[J].计算机工程与应用，2008，44（27）：236-239.

[11]YANG Jian-ren.A Dynamic Route Guidance Algorithm Based on Modified Ant Colony Optimization[C]//Computer Network and Multimedia Technology.Wuhan:IEEE,2009: 1-3.

[12]周明秀，程科.动态路径规划中的改进蚁群算法[J].计算机科学，2013，40（1）：314-316.

[13]党希望.基于主次种群蚁群算法的动态路径优化研究[D].成都：西南交通大学，2013.

[14] 刘伟.基于蚁群算法的动态路径诱导研究[D].成都：西南交通大学，2008.

[15]董永峰，刘艳柳，张娜.基于改进蚁群算法的动态多路径诱导系统研究[J].河北工业大学学报，2010，39 （3）：46-51.

[16] 林娜，霍志胜.一种基于免疫遗传的多路搜索蚁群动态路径诱导算法[J].小型微型计算机系统，2013（3）：590-594.

[17]HUANG Yan-guo,LUO Qiang.Dynamic Path Optimization Method Based on Ant Colony Algorithm and Group Deci⁃sion-making[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation.Beijing:IEEE, 2012:300-304.

[18]牛新征，佘堃，路纲.蚁群算法研究的新进展和展望[J].计算机应用研究，2007，2（4）：12-15.

[19]Holland J H.Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology,Con⁃trol,and Artificial Intelligence[M].Ann Arbor:The Univer⁃sity of Michigan Press,1975.

[20]WEN Hui-min,YANG Zhao-sheng.Study on the Shortest Path Algorithm Based on Fluid Neural Network of In-Vehi⁃cle Traffic Flow Guidance System[C]//Proceedings of the IEEE International Conference on Vehicle Electronics. Changchun:IEEE,1999:110-113.

[21]Hitoshi Kanoh,Hideki Kozuka.Evaluation of GA-Based Dynamic Route Guidance for Car Navigation Using Cellu⁃lar Automata[C]//Intelligent Vehicle Symposium.IEEE, 2002:178-183.

[22] 张水舰，李永树.利用GA和GIS的动态路径诱导算法[J].武汉大学学报：信息科学版，2009，34（12）：1476-1479.

[23]邹亮，徐建闽.基于遗传算法的动态网络中最短路径问题算法[J].计算机应用，2005，25（4）：742-744.

[24]李松江.基于改进遗传算法的动态路径诱导系统的研究[D].长春：长春理工大学，2010.

[25]李春元，魏武.基于改进遗传算法的最优路径求解[J].交通与计算机，2007，25（5）：88-92.

[26] 孙霞，黄席樾.基于改进遗传算法的城市交通路径诱导系统的研究[D].重庆：重庆大学，2007.

[27]赵丹.城市交通路径诱导算法研究[D].西安：长安大学，2009.

[28]Mainal M K,Mabu S,Hirasawa K.Pruning High-Level Net⁃work Using Genetic Algorithm for Efficient Hierarchical Route Planning in Road Networks[C]//IEEE Annual Confer⁃ence.Tokyo:IEEE,2011:2903-2909.

[29]Chang W A,Ramakrishna R S.A Genetic Algorithm for Shortest Path Routing Problem and the Sizing of Popula⁃tions[J].IEEE Transactions on Evolutionary Computation, 2002,6(6):566-579.

[30]DING Zhen,Leung Henry,ZHU Zhi-wen.A Study of theTransiently Chaotic Neural Network for Combinatorial Opti⁃mization[J].Mathematical and Computer Modeling,2002, 36(2):1007-1020.

[31]Bo-Yang Q U,Ponnuthurai Nagaratnam Suganthan,Shi-Zheng Zhao.Current Position-Based Fitness Euclideandistance Ratio Particle Swarm Optimizer for Multi-Modal Optimization[C]//Nature and Biologically Inspired Comput⁃ing.Fukuoka:IEEE,2011:383-388.

[32]Glover F.Future Paths of Integer Programming and Links to Artificial Intelligence[J].Computer and Operations Research,1986(5):533-549.

[33]LV Guang-ming,SUN Xiao-meng,WANG Jian.A Simulat⁃ed Annealing-New Genetic Algorithm and its Application [C]//Electronics and Optoelectronics.Dalian:IEEE,2011: 246-249.

[34]李菲，肖洪祥.基于神经动态规划算法的最优路径选择[J].桂林工学院学报，2009，29（1）：54-57.

[35]马艳丽，裴玉龙.基于混沌神经网络的驾驶员动态路径诱导算法研究[J].交通运输系统工程与信息，2007，7 （1）：57-60.

[36]吴成东，杨丽英，许可.神经网络和遗传算法在动态路径诱导中的应用[J].计算机应用研究，2006（5）：177-179.

[37]CHEN Qun.Dynamic Route Guidance Method Based on Particle Swarm Optimization Algorithm[C]//2009 Second International Conference on Intelligent Computation Tech⁃nology and Automation.Changsha:IEEE,2009:267-270.

[38]陈曦.粒子群优化算法的改进及在动态交通分配问题中的应用[D].长沙：长沙理工大学，2007.

[39]DENG Yan-fang,TONG Heng-qing,et al.Dynamic Short⁃est Path in Stochastic Traffic Networks Based on Fluid Neu⁃ral Network and Particle Swarm Optimization[C]//2010 Sixth International Conference on Natural Computation. Yantai:IEEE,2010:2325-2329.

[40]杨清波.GIS环境下的动态交通最优路径算法研究[D].长沙：中南大学，2012.

[41]李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践，2002，22 （11）：32-38.

[42]FU L P,LRILETT R.Expected Shortest Paths in Dynamic and Stochastic Traffic Networks[J].Transportation Re⁃search B,1998,32(7):499-516.

New Trends of Dynamic Route Guidance Methods Based on Intelligent OptimizationAlgorithms

YOU Yao,LIN Pei-qun
(School of Civil Engineering and Transportation,South China University of Technology, Guangzhou 510640,China)

Some representative intelligent optimization algorithms in the dynamic route guidance meth⁃ods were discussed and summed up by the review method,which laid a foundation for the future research in the intelligent transportation system deeply and widely.The improvement mechanism and the applica⁃tion results of the intelligent optimization algorithm are analyzed from the view of the algorithm character⁃istics,improvement effect,performance evaluation,etc.And the basic idea,advantages,disadvantages and limitations of these algorithms were given.Besides,the research status of evaluation methods of the intelligent optimization algorithm performance was analyzed,which helped engineers and researchers to select the most suitable variability modeling techniques.Finally,combining with the analysis results of algorithms application,the application prospect and some important research directions in the future fur⁃ther research of the intelligent optimization algorithms in intelligent transportation system were forecast. Key words:dynamic route guidance methods;research progress;intelligent optimization algorithms; ant colony optimization;genetic algorithm

U495

A

2095-9931（2015）01-0020-07

10.16503/j.cnki.2095-9931.2015.01.004

2014-10-22