关于一阶矩阵的再认识与诠释
常秀芳,李映波,李 高
(1.山西大同大学煤炭工程学院,山西大同 037003;2.内蒙古自治区乌海市海勃湾区煤炭局,内蒙古乌海016000)
关于一阶矩阵的再认识与诠释
常秀芳1,李映波2,李 高1
(1.山西大同大学煤炭工程学院,山西大同 037003;2.内蒙古自治区乌海市海勃湾区煤炭局,内蒙古乌海016000)
对一阶矩阵与数或与数学式子及其二次型之间的表述,提出了新的看法,给出了新的具体的表述方式,指出行矩阵与列矩阵的乘积和向量的内积、数量积概念的不同之处,并得出两个结论。
一阶矩阵;行矩阵;列矩阵;内积;数量积;二次型
在教学实践中,翻阅了大量的高等代数和线性代数[1-3],注意到,行矩阵与列矩阵乘积运算成一阶矩阵,或遇到一阶矩阵后,往往认其为一个数,这与矩阵概念是相悖的,并由此产生一系列的问题,为此提出了给出了新的具体的表述方式,予以商榷。
1 一阶矩阵
定义1矩阵是由m×n个数排成的m行n列的一个数表,为了表示它是一个整体,并用括号括起来,记作

当m=n时,即行数和列数相等的矩阵,称为n阶矩阵或n阶方阵。
定义2在n阶方阵中,只有一行和一列的矩阵,称为一阶矩阵。
一阶矩阵是只有一个元素的矩阵,它是阶数最小的方阵,在n阶方阵中,是没有零阶矩阵的。
在一阶矩阵A=(a)中,如果a=0,则矩阵A=(0)称为一阶零距阵;如果a≠0,则矩阵A=(a)是一阶可逆矩阵,其逆矩阵为;如果a=1,则矩阵A=(1)是一阶单位矩阵。
由于矩阵是一个数表,它不表示任何具体的数值,因此,一阶矩阵A=(a)也是一个数表。从而矩阵(a)与a两者之间有着本质的区别,前者是一个数表,后者是一个具体的数,绝对不能把矩阵(a)与数a等同起来。可是大量的教材或参考资料中,把一阶矩阵竟然说成是一个数,这是一种错误的表达,必须引起注意,予以纠正。
2 行矩阵与列矩阵的乘积
如果只有一行的矩阵称为行矩阵,也称为行向量;如果只有一列的矩阵称为列矩阵,也称为列向量。
行向量(行矩阵)和列向量(列矩阵)是特殊的矩阵,以及由向量的内积、数量积和矩阵的概念知。
结论1同维的两个行矩阵(行向量)或两个列矩阵(列向量)是不能做矩阵乘积运算的,只能作内积或向量的数量积,其结果是一个数值。
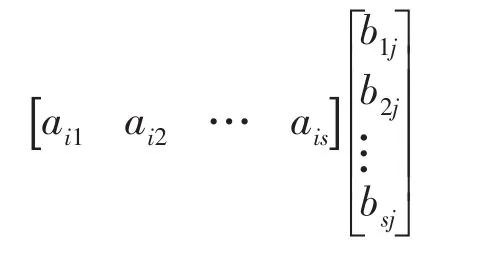
结论2同维的行矩阵(行向量)与列矩阵(列向量)是不能作内积或向量的数量积,作为只有一行或只有一列的特殊矩阵,只能做矩阵相乘运算的,其结果并不是一个数,而是一个一阶距阵,即
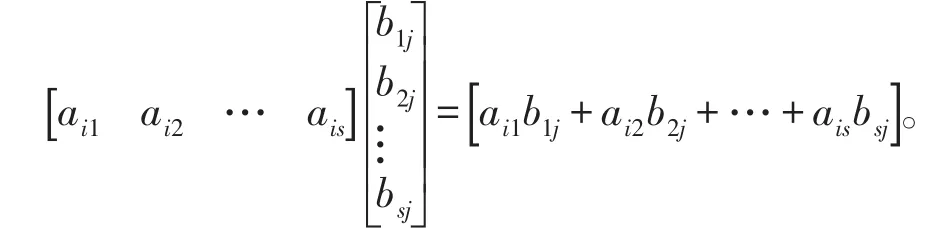
可是教材或参考资料中,大量把

错误地表述或写成是一个数ai1b1j+ai2b2j+…+aisbsj,更有甚者数与矩阵的运算不分,如把矩阵乘积定义中,一个m×s矩阵A=(aij)m×s与一个s×n矩阵B=(bij)s×n的乘积矩阵C=(cij)m×n的元素cij错误地写成等于距阵的积,又等于一个数的错误形式,例如
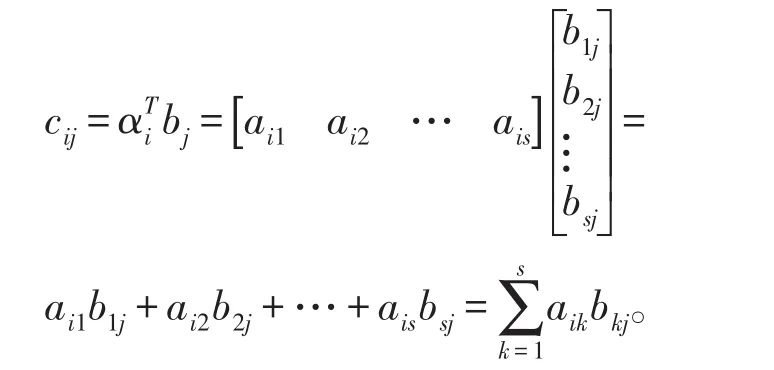
其正确的书写为

3 一阶单位矩阵
矩阵E1=(1),因对任何一个一阶矩阵A,有E1A=AE1=A,所以E1=(1)是一阶单位矩阵。
一阶单位矩阵中是没有任何零元素的,它是比较特殊的一阶距阵,只有一个元素,而且元素是1,但并不表示它就是1,有的教材把XTX=E1写成XTX=1或说成是1都是错误的,须予以纠正。
4 二次型
所以在推导二次型的矩阵形式过程中,或用矩阵表示时,甚至用矩阵作正交变换等内容时,都必须对二次型加以括号才能和矩阵相等。例如,在推导过程中,则应为

则应为[f]=xTAx。
在正交变换中,则存在正交矩阵Q,作正交变换x=Qy,则应为
5 结束语
综上所述,对于一阶矩阵中的种种易混淆的内容必须引起大家的注意,歧异的或错误的内容在教材或教参中必须消除和纠正,在内容的编排上必须融有正确的、严谨的、科学的、负责的态度。
[1]同济大学数学系.线性代数[M].北京:高等教育出版社,2012.
[2]吴传生,王卫华.线性代数[M].北京:高等教育出版社,2004.
[3]常秀芳,李高.伯努利方程的几种新解法[J].雁北师范学院学报,2007,23(2):89-91.
[4]李高,常秀芳.不定方程x2+y2+z2=2(xy+yz+xz)的解及其性质[J].山西大同大学学报,2011,27(3):6-10.
[5]李高,常秀芳.二阶变系数线性微分方程及其衍生方程[J].河北北方学院学报,2011,27(5):13-15.
[6]李高,常秀芳.关于二阶变系数线性微分方程求解法的研究[J].河北北方学院学报,2010,26(6):12-14.
[7]李高,李殊璇,常秀芳.二阶变系数线性微分方程可解的研究[J].河北北方学院学报,2013,29(2):1-2.
[8]常秀芳,李高.Taylor幂级数直接展开的新方法[J].河北北方学院学报,2013,29(5):1-3.
Interpretation of First Order Matrix
CHANG Xiu-fang1,LI Ying-bo2,LI Gao1
(1.School of Coal Engineering,Shanxi Datong University,Datong Shanxi,0370031;2.Coal Bureau of Haibowan District,Wuhai city,Innre Mongolia׀,Wuhai 016000)
Of first-order matrix and the number or and mathematical formulas and quadratic expression between,this paper puts forward a new view,gives a new concrete way of expression,points out the row matrix and column matrix and vector inner product,the difference between the inner product and the scalar product,and two conclusions.
first-order matrix;row matrix;column matrix;inner product;scalar product;quadratic form
O175.14
A
1674-0874(2015)04-0009-03
2014-10-20
山西大同大学教学改革资金资助项目[XJY2013211]
常秀芳(1965-),女,山西朔州人,副教授,研究方向:大学数学教育。
〔责任编辑 高海〕

