Study of high-speed interaction processesbetween fluoropolymerprojectiles and alum inum-based targets

Evgeny A.KHMELNIKOV*，A lexey V.STYROVKonstntin V.SMAGINNtli S.KRAVCHENKOVlery L.RUDENKO，Vldim ir I.FALALEEV，Sergey S.SOKOLOV，Artem V.SVIDINSKY，Ntli F.SVIDINSKAYA

aNizhny Tagil Technological Institute（Branch）of Ural Federal University，Russian Federation

bFederal State Enterprise“Nizhny Tagil Institute ofMetal Testing”，Russian Federation

cAll-Russian Scientific Research Institute of Experimental Physics，Sarov，Russian Federation

Received 30 March 2014；revised 13 August2014；accepted 1 September 2014 Available online 26 December 2014

Study of high-speed interaction processesbetween fluoropolymerprojectiles and alum inum-based targets

Evgeny A.KHMELNIKOVa，*，A lexey V.STYROVa，Konstantin V.SMAGINa，Natalia S.KRAVCHENKOa，Valery L.RUDENKOb，Vladim ir I.FALALEEVb，Sergey S.SOKOLOVc，Artem V.SVIDINSKYc，Natalia F.SVIDINSKAYAc

aNizhny Tagil Technological Institute（Branch）of Ural Federal University，Russian Federation

bFederal State Enterprise“Nizhny Tagil Institute ofMetal Testing”，Russian Federation

cAll-Russian Scientific Research Institute of Experimental Physics，Sarov，Russian Federation

Received 30 March 2014；revised 13 August2014；accepted 1 September 2014 Available online 26 December 2014

The experimental results and numericalmodeling of penetration process of fluoropolymer projectiles in alum inum-based targets are presented.Analysis ofmathematicalmodels for interaction of elastoplastic projectile and targetw ithout taking additional energy released during interaction of fluoropolymer and alum inum into consideration is carried out.Energy fraction which is spent effectively on the increase in cavity volume is determined.The experimental and calculated results of penetration by combined and inert projectiles are compared.

Reactivematerials；Fluoropolymer；High speed strain；Interaction；Aluminum；Titanium alloy；Numericalmodeling

1.Introduction

A prom ising direction in arm s development is an application of“reactivem aterials”instead of inert ones in its design. One of the firstworks in this direction was the experiments carried out in Ural Federal University during 1984 and 1988［1，2］.In the USA，the firstworks on reactivematerials were published in the late 1990s and the early 2000s.Beside USA，UK and Chinaarealso involved in research and testing of new principles of damage increase for kinetic，shaped charge and fragmentation projectiles，including the reactivematerials in their design.Application of reactivematerials could allow to solve aw ide range of tasks in the future-from increasing the damage and effectivenessof the projectiles to enhancing their safety and reliability.

One of the components ofmodern m ixture reactivematerials is fluoropolymer（TFE）.Fluoropolym er has the ability to develop chemical reactionswith energy released under certain conditions，not only under static loads and heating［1-3］，but also under high-speed deformation togetherw ith targets containing aluminum［4-6］.The goal of the investigation is to determine the behavior of fluoropolymer under the condition of dynam ic high-speed loading during its interaction w ith titanium alloy，and also to determine the behavior of target material.

2.Experimental resu lts

Additional energy，which is released in the exothermic chemical reactions of fluoropolymer，is transferred into a mechanicalwork on cavity expansion in target；the amountof effective work increases w ith the impact velocity.In order tocheck this effect，the experimental data of dynam ic interaction of textolite and monolith metal projectiles containing fluoropolymer and inert filler w ith semi-infinite targets from alum inum alloys AlMn1 and D16-AT was comparatively analyzed.

Projectiles with d0=0.013 m and elongationλ=L0/ d0=2.4，where L0is projectile length，were used in the experiments.The experimental results are presented in Tables 1 and 2.After the experiments，the cavity parameters in targets were measured（Fig.1）.The depth hcav，diameter dcav，and volume Wcavof cavity were determ ined.

The cavity in the sem i-infinite target is formed by the kinetic energy of the projectile and partially by the energy released from thermochemical reaction of fluoropolymerw ith alum inum-based target.The energy balance equation can be w ritten as

where E0is kinetic energy of the projectile；Echis energy released during chemical reaction and spent on cavity formation；Eepisenergy spenton elastic and plastic deformation of the projectile；and Ecavisenergy spenton cavity formation.

The amount of energy spent on cavity formation for undeformable projectile can be determ ined by the amount of specific displacementwork Aspof targetmaterial.

where h，hfare current and final penetration depth，respectively；F，E0are target resistance force and kinetic energy of the impact，respectively；Wcavis cavity volume.

Table 1 Cavity parameters from fluoropolymer projectile impact（d0=0.013 m，λ=2.4）on a AlMn1 target.

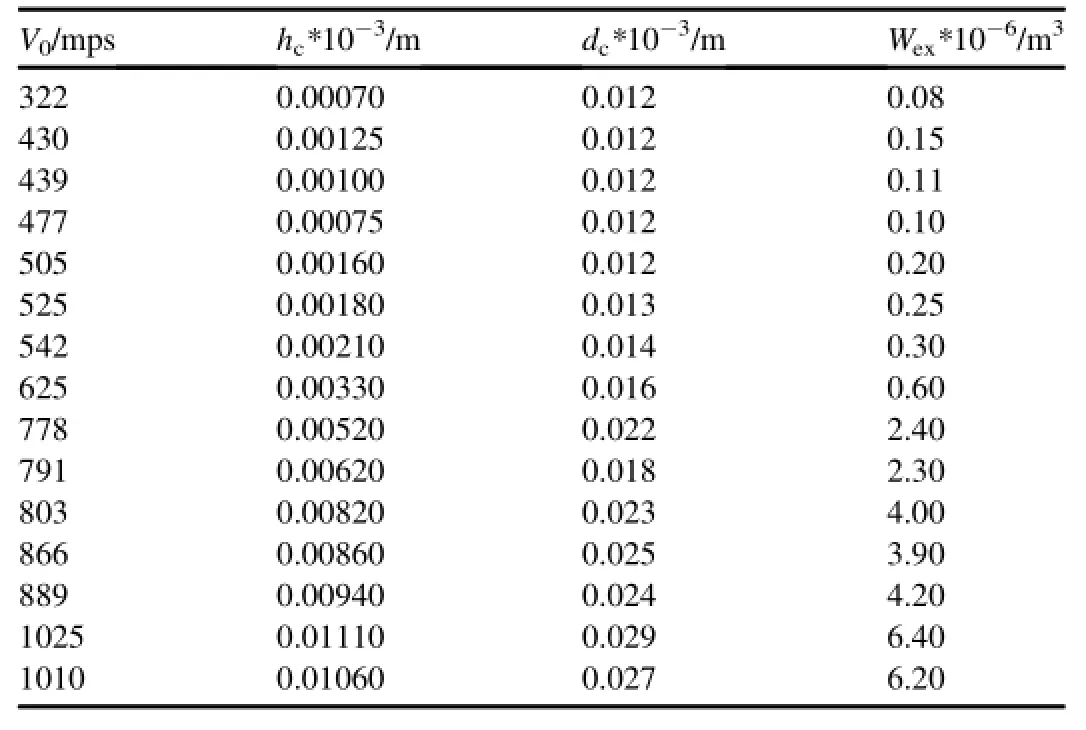
Table 2 Cavity parameters from fluoropolymer projectile impact（d0=0.013 m，λ=2.4）on a D16-AT aluminum alloy target.

Fig.2 shows the results for the experimental determination of the specific displacementwork Aspfor fluoropolymer，textolite and steel projectiles.The analysis of the results shows that the specific displacementwork necessary for the formation of the cavity w ith same volume in the fluoropolymer strikers is less than that in the steel strikers.

Fig.1.M easured parameters hcavand dcavof sem i-infinite target.

Aspwas determ ined based on the method of continuous acceleration registration during reverse ballistic experiments.

In order to determ ine the specific displacement work of material targets，the experiments on penetration of undeformable projectile（d0=0.005 m and elongationλ=10）were carried out.The nose part of projectilewas a conew ith α=60°.The targets AlMn1 and D16-AT were 80 mm in thickness w ith Brinnell hardness of 30 MPa and 43.5 MPa，respectively.The obtained results are presented in the form of functional relations

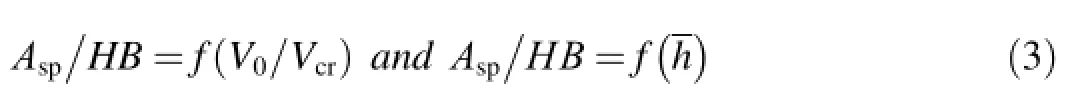
The critical velocity［7］is expressed as

The value of critical velocity was determined from the hardness of the projectiles，which is equal to 663 mps for AlMn1 and 788 mps for D16-AT alloy.The functional dependencies for both alloys in the ascending branch of thecurve（in Fig.3）can be expressed w ith a second-order polynomialand have the follow ing shape，for example，for AlMn1

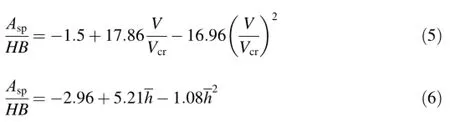
Fig.2.Specific displacement work for target material A lM n1 from impact velocity.

After the maximal penetration is achieved in the deep layers of the target（h≥2.5 d0），the specific displacement work stays constant（Fig.3）.

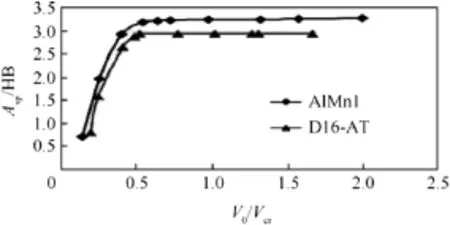
Fig.3.Dependency of Asp/HB=f（V0/Vcr）.

3.Penetration m odeling

In order to determine the amount of energy used on elastoplastic deformation Eep，the penetration of fluoropolymer projectile into semi-infinite aluminum-based alloys under the same experimental conditionsmentioned above（Tables 1 and 2）was test.The projectile was considered an elastoplastic body，and no additional thermochemical energy was assumed to be released during the penetration.

Thecalculationsweremadew ith thesoftwarepackageTIM-2D［8］designed for calculationsof two-dim ensionalcontinuum m echanics problems on unstructured polygonal Lagrangian meshesw ith arbitrary numberof connections Fig.4.

Fig.4.Initial set-up of fluoropolymer projectile interaction w ith target.

3.1.The equation of state and elastoplastic qualities of fluoropolymer projectile

3.1.1.The equation of state of fluoropolymer projectile

The equation of state of fluoropolymer projectile was calculated from three-term Zababakhin equation of state［9］. In the equation of state，two parts are distinguished for pressure and unit internal energy calculation

where PC，ECare the potential（“cold”）components of pressure and unitenergy，respectively；and PT，ETare the thermal components of pressure and unitenergy，respectively.

Potential pressure and potential energy are calculated by the relations

whereδ=ρ/ρ0is relative compression；ρ0ismaterial density under normal conditions；ρis currentmaterial density；C0is speed of sound in monolith uncompressed material；and n is adjustable parameter.

Thermal pressure is calculated by

where ET=E-Ec，andΓis Gruneisen coefficient.

Gruneisen coefficientΓisexpressed through parameter hΓ，which characterizes the value of lim it material com pression（maximal density）that could be reached in the calculations of shock adiabat

Thermal energy can be expressed as heat capacity multiplied by temperature ET=CV·T.This gives an opportunity to w rite the thermodynam ic functions.This form of equation of state allows tow rite the relations for free energy and entropy

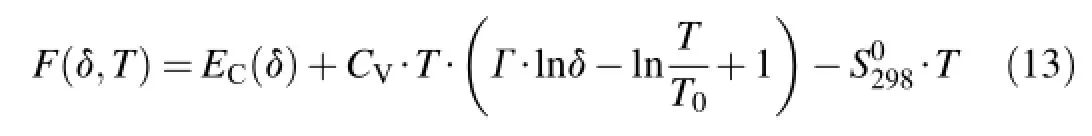
where T0is temperature at norm al conditions，which determines the start of entropy calculations（in the equation of state T0=298 Kis standard value of entropy.

From Eq.（13）for entropy calculation

In the equation of state，the parameters have follow ing values：ρ0=2190 kg/m3-initial material density；C0=2045 mps-speed of sound in uncom pressed cold material；n=4.972-power parameter in the relationship PC（δ）；γ=Γ+1=2.481，whereΓisGruneisen coefficient；Cv=1 kJ/gK-specific heat capacity.

In the second case，fluoropolymer was calculated w ith the equation of state of polymermaterials form［10］.

3.1.2.Elastoplastic qualities of fluoropolymer projectile

Consideration of fluoropolymer elastoplastic qualities was m ade w ith the help of two models：Von M ises：For calculations Y0（yield stress）was set to 0.15 GPa，or-0.035 GPa；Shemyakin：In the Shem yakin m odel，Y0is a linear function of thermal energy；thermal softening is taken into consideration.

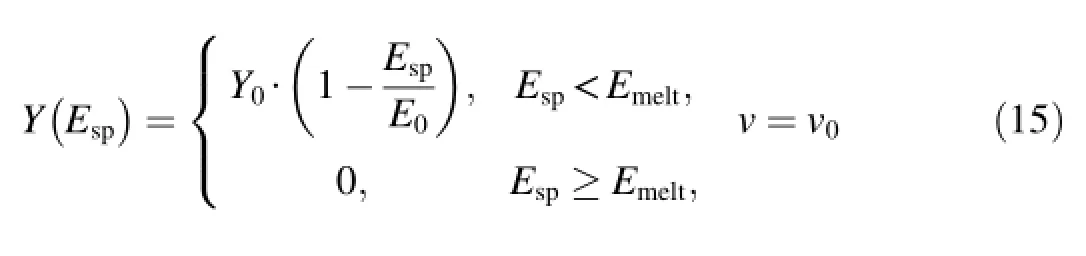
where Y0is yield stressunder normal conditions；Espis thermal componentof specific internalenergy；Emeltiseffective energy ofmaterialmelting；andνis Poisson's ratio.K=ρ·C2Sisbulk modulus，and Poisson's ratioνischosen asamain independent elasticity parameter.Shearmodulus is calculated as

3.2.The equation of state and elastoplastic qualities of target

3.2.1.The equation of state of target

For aluminum-based targets，the equation of state was calculated from Zababakhin's equation w ith maximal density reduced to standard conditions.The thermodynam ic qualities of aluminum alloy target are described w ith M ie-Gruneisen equation of state w ith variable Gruneisen coefficient and reduced to standard conditions.

3.2.2.Elastop lastic qualities of target

The elastoplastic qualities of AlMn1 were taken into consideration using threemodels.（a）Von M isesmodel［13］.

In its standard form，Y0=0.18 GPa andν=0.32.（b）Johnson-Cookmodel［14］.

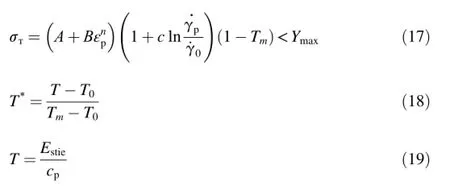
whereσтis yield point；m is parameter of thermal loss of strength，m=1；A is yield pointw ith quasistatic tension or contraction，A=0.18 GPa；B，n are deformation hardening parameters，B=0.426 GPa，n=0.34；c isdynamic hardening parameter，c=0.015；γ.0=1061/ms is fixed multip lier of d.eformation velocity，γ0=1061/ms；isplastic deformation；γpis velocity of plastic deformation；Ymaxismaximum of yield point，Ymax=0.7 GPa；T0is initial temperature，T0=293 K；Tmis temperature calculated by Lindemann's law；cpis heat capacity，cp=0.00875 kJ/g·К；and Estieis specific thermal interior energy（kJ/g）.

（c）Glushak model

The determ ination the equations for viscoplastic Glushak m odel is dependent on the deformation rate.In this case，a yield condition becomes heterogeneous w ith respect to time variable because this condition contains a scale material parameter-relaxation timeτγ.Yield stress is a sum of two functions：Glushak yield function YS（εp，P，T）and a viscoplastic term.

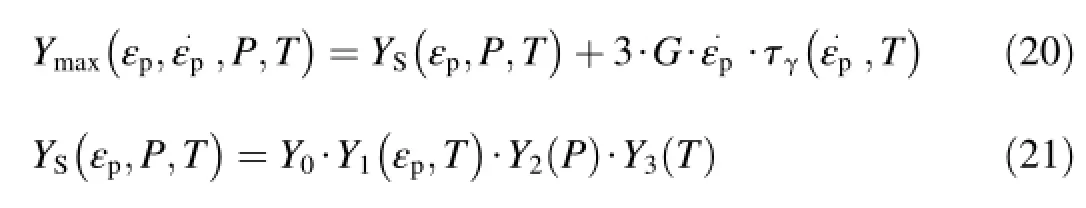
where Y1（εp，T），Y2（P），Y3（T）are the functionsof deformation and com pression hardening and therm al softening，respectively.Deformation hardening multip lier depends on plastic intensity deformation and temperature

M ultiplier of compression loss of strength is expressed as

where P is total pressure.M ultiplier of thermal lossof strength is expressed as

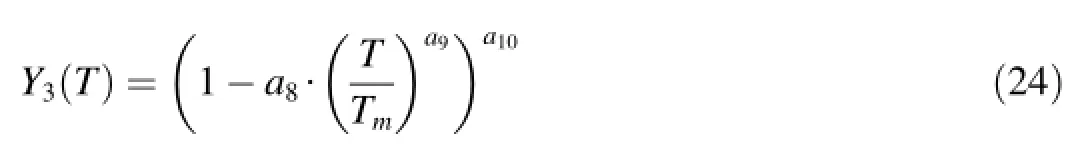
where T is current temperature；a1，…，a10are empiric constants；andεpis accumulated plastic deform ation.

The shearmodulus defines a deviator component of stress tensor for elastic field

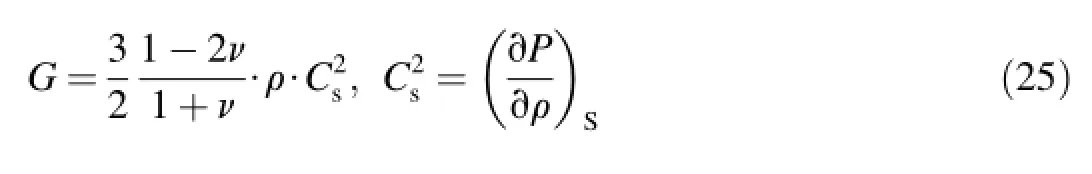
whereρis density of matter；and CSis current volumetric acoustic velocity.

Poisson's ratio depends on dimensionless parameter T/Tm

whereν0，c，k are constant coefficients.

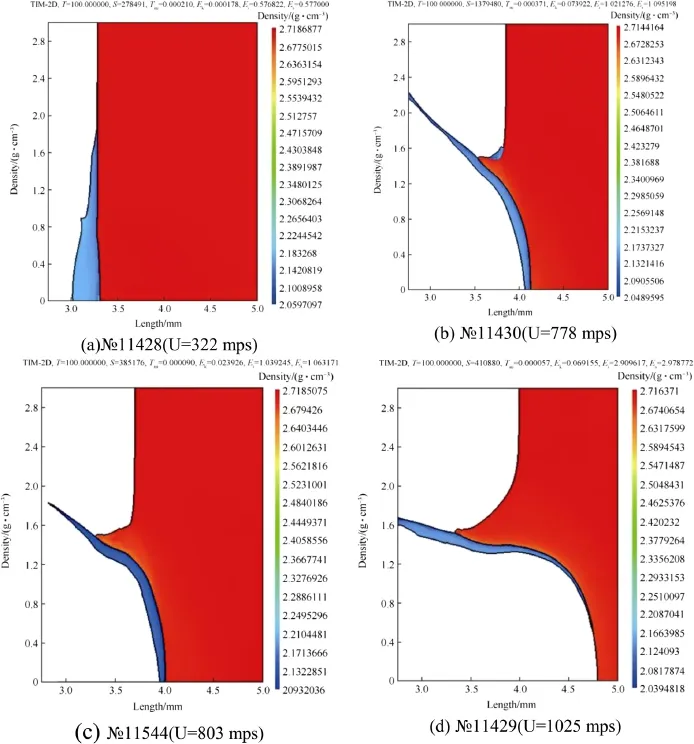
Fig.5.The density distribution at time t=1000 mks and different impact velocities using M isesmodel for D16 target.

Follow ing valueswere used in calculations：Y0=0.18GPa -yield stress for AlMn1 alloy and Y0=0.28GPa for D16-AT；a1=1.4，a2=1，a3=2，a4=1，a5=2-deformation hardening parameters；a6=0.08 GPa-1，a7=1-compression hardening parameters；a8=1，a9=1，a10=1-thermalsoftening parameters；v0=0.268，c=0.8657，k=1-parameters describing Poisson's ratio temperature dependence.

Fig.6.The density distribution at time t=1000mks and different impact velocities using Glushak model for D16 target.

4.Comparison ofm odeling and experim ental results

Figs.5 and 6 show the cavities obtained in numerical calculations for different impact velocities and target parameters according to the von M ises model and Glushak model，respectively.

Comparison of the results w ith experimental data（Fig.7）show s thatallm odels show a good agreementw ith experiment in the description of cavity diam eter.It is possible to conclude that the cavity formation，especially at the initial stage of penetration，is caused only by projectile kinetic energy.

Additionalenergy of thermochem ical reaction hasnotbeen released yet.Release of this energy is delayed，thus its influence starts to appear in the deeper layers，which leads to an increase in the penetration depth.This can explain the significant difference in the calculated and experimental penetration depths.

Amount of additional chem ical energy can be determined as

Fig.7.The relationship among cavity dimensions（diameter and depth）and velocity of fluoropolymer projectile interactionw ith D16-AT target.

The calculated results for D16-ATarepresented in Tables3 and 4.In Table3，the calculations labeled as“Glushak 1”were made with von M ises model for fluoropolymer with Y0=0.15 GPаand Glushakmodel for D16-AT.Calculations labelled as“Glushak 2”weremadew ith von M isesmodel for fluoropolymer w ith Y0=0.35 GPаand Glushak model for D16-AT.

Unfortunately，the form at of the article does not allow to presentamore detailed analysis of the calculations carried out w ith themodels.However，the results shown in Fig.6 show that the results calculated using thesemodels have the same trend as those calculated using the basic model（Table 3）.

Analysis of the results（Table 3 and Fig.7）shows that the proportion of the chemical energy decreasesw ith the increase in the interaction velocity for all models，except Johnson-Cook model，which contradicts w ith physical concepts and experimental data［1］.

In Tables 3 and 4：V0is velocity of fluoropolymer penetration into the targetmps；are experimental and calculated volumes of cavity，cm3；Echis energy released by chemical reaction between fluoropolymer and aluminum of target，kJ；Glushak 1 is the elastic plastic states of fluoropolymer calculated by M isesmodel w ith Y0=0.15 GPa and AlMn1 calculated by Glushak model w ith Y0=0.18 GPa；Glushak 2 is the elastic plastic states of fluoropolymer calculated by M isesmodelw ith Y0=0.035 GPa and AlMn1 calculated by Glushak modelw ith Y0=0.18 GPa.

In other cases，the elastic plastic states of fluoropolymer were calculated by M isesm odelw ith Y0=0.035 GPa，and the elastic plastic statesof A lMn1 and D16-ATwere calculated by Glushak and J-Cook and M isesmodels.

The quantity of chem ical energy spent in cavity form ing obtained by the calculations based on the Johnson-Cook model is in sufficiently good agreementw ith the experimental results.

Experimental dependence for Echwas determined by comparing the cavity volumes produced by the penetration of fluoropolymer projectiles and those made of inert material w ith the same density and geometrical dimensions into semiinfinite AlMn1 target（Fig.8）.

The chem ical reaction of alum inum w ith fluoropolym er proceeds as follow sw ith the release of a significant portion of therm al energy

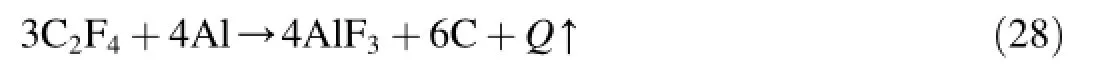
The amount of thermal energy for 3 mol of reacting fluoropolymer is Q=897 kJ［11，12，13］.Projectile mass mp=8.6 g，andmolarmassμ（C2F4）=100 g/mol.Theamount of chemicalenergy released in full thermochemicaldestruction of fluoropolym er can be determ ined from the relation

where N is the number of reactingmoles，N=3.

As a result，the effective projectilemass used in the thermochem ical reaction to increase the volume of cavity in the semi-infinite target equals

Analysis of the plots in Fig.9 shows that the obtained effectivemass of projectile doesnot exceed 20%of its initial mass.In order to improve the effectiveness of the released energy，it is possible to use the preformed fragments w ith a solid shell.

Table 3 The energy released in a chem ical reaction during penetration into the targetmade of D16-AT.

Table 4 The energy released in a chem ical reaction during penetration into the targetmade of A lMn1.

5.Conclusions

One of the components ofmodern mixture reactivematerials is fluoropolymer（TFE）.Fluoropolymer has the ability to develop chem ical reactionsw ith energy released under certain conditions，not only under static loads and heating，but also under high-speed deformation togetherw ith targets containing alum inum.

Conducted studies allowed to determine the behavior of fluoropolymer under the condition of dynamic high-speed loading during its interaction w ith titanium alloy，and also to determine the behavior of targetmaterial.And we have done such conclusions：

1）The proportion of the chem ical energy released by the reaction between fluorine and target material was determ ined effectively to increase the volume of cavity.

2）The mass fraction of the projectile spent on effective chemical energy was determined.It was shown that the effective mass fraction of the unjacketed projectile does notexceed 20%.One of the possibleways to increase the effectivemass is to create a preformed fragmentw ith thinwalled shell.Wall thickness should be optimized w ith respect to effective energy.

3）The m odel that accurately describes fluoropolymer projectile penetration into aluminum-based targetwaschosen w ithout taking into accountenergy of the thermo oxidation reaction.In the future，the assessment of the possible influence of chemical reaction for reactivematerialsand the evaluation of its influence on the penetration and cavity parameters will be conducted.This can be done by introducing the kinetics of the slow energy releasewhich appears behind the shock wave front as a result of chem ical reaction between the reactive material components.

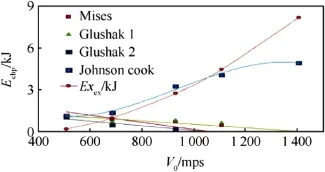
Fig.8.Energy released in the reaction between fluoropolymer and target material AlMn1.

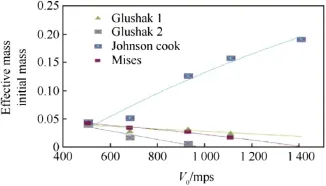
Fig.9.Mass fraction of fluoropolymer projectile reacted w ith a targetmade of A lMn1.

［1］Styrov AV，Selivanov VV，Osipov AI，Khmelnikov EA.Study of the interaction processbetween alum inum and fluoropolymer in a high-speed collision.In：Electrophysics of combustion.Proc.of XIII all-union workshop.Cheboksary；1990.p.63-4.

［2］Styrov AV，Selivanov VV，Khmelnikov EA.Influence of the temperature on the interaction between alum inum and fluoropolymer in a high-speed collision.In：Proc.of III National Seminar“Dynamic strength and resistance to cracking of structuralmaterialduring single impulse loads”，Kyiv；1991.p.62-3.

［3］M iller P.J.，Lindfors A.J.Shock induced detonation-like reactions in metal/teflon systems.In：International workshop on new models and numerical codes for shock wave processes in condensedmedia.-Oxford，UK.15-19 September 1997，pp.75-79.

［4］Davis J，Lindfors A，M iller P，Finnegan S，Woody D.Detonation like phenomena in metal e polymer and metal/metal oxide e polymermixtures.In：Proc.of XI Intern.Detonation Symposium，Colorado；1998. p.24-7.

［5］Catalog.Improved and new alum inum and titanium alloys in aircraft design645.Moscow：TsAGI；1984.p.25-6.

［6］Bazanyants SN.Aircraft damage control.Moscow：Voenizdat V；1983. p.134-7.

［7］Khmelnikov EA，Gladkov NA，Yachnik OE.On the deformation rate influence on the dynamic yield stress of the projectile material.In：Proceedings of the MSTU N°557.Moscow：MGTU；1992.p.97-106.

［8］Sokolov SS，Voropinov AA，Novikov IG，Panov AI，Sobolev IV，Pushkarev AA.TIM-2D method for the calculation of continuum mechanics on irregular polygonal meshes w ith an arbitrary number of connections in the nodes.Issue 4.In：Problems of Atomic Science and Technology.Ser.Mathematicalmodeling of physical processes；2006. p.29-44.

［9］Zababakhin EI.Some questions of gas dynamic explosion.Snezhinsk 1997：83-7.

［10］Bushman AV，Lomonosov IV，Fortov VE，Khishchenko KV.Theequation of state of saturated organic compounds at high pressures.Chem Phys 1994；13（5）：97-107.

［11］Styrov AV，Selivanov VV.Chem Phys1999；18（11）：72-8.

［12］Styrov AV，Selivanov VV.Experimentalstudyof theinteractionofaluminum w ith PTFEunderofshock loadingconditions.In：Proc.Of Intern.Conference“Shockwavesin condensedmatter”.-St.Petersburg；1998.p.133-4.

［13］Segalman DJ，Fulcher CWG，Reese GM，Field Jr RV.An efficient method for calculating RMS von M ises stress.Sandia Report，SAND98-0260.1998.p.23-4.

［14］Johnson GR，Cook WH.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures.Eng Fract Mech 1985；21（1）：31-48.

.

E-mail addresses：khmelnikov7@gmail.com，xea07@rambler.ru（E.A. KHMELNIKOV）.

Peer review under responsibility of China Ordnance Society.

http：//dx.doi.org/10.1016/j.dt.2014.09.006

2214-9147/Copyright©2014，China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

Copyright©2014，China Ordnance Society.Production and hosting by Elsevier B.V.A ll rights reserved.