用人体平面刚体模型分析太极拳在水平作用力下的力学原理

顾 杰，郭振兴，吕 蒙

（邯郸学院 太极文化学院，河北 邯郸 056005）

太极文化研究

用人体平面刚体模型分析太极拳在水平作用力下的力学原理

顾 杰，郭振兴，吕 蒙

（邯郸学院 太极文化学院，河北 邯郸 056005）

为实现太极拳的力学分析，率先提出和建立了人体平面刚体模型。刚体模型简括了人体构架、质量、速度、水平攻击力、重力、地面反力、摩擦力等因素。应用该模型对太极拳进行水平作用力下的力学分析，得出了五个重要结论，即人体的重心要在支撑面内以维持稳定平衡；脚底打滑和失根是维持稳定平衡的两种临界条件；在临界条件内人体平衡，超过任何一个临界条件将导致人体失去平衡；水平攻击力来自脚底的摩擦力、人的整体动量和肢体相对运动的动量；内劲造就动量和传递力。还通过数学计算，推导出太极拳套路训练和推手竞技中保持平衡的临界条件和相应计算公式，并用算例演示了太极拳“发劲如放箭”、“引进落空”、“牵动四两拨千斤”等技术技巧的力学原理，为太极拳的运动生物力学深入研究奠定了基础。

太极拳；力学分析；人体平面刚体模型

太极拳属于体育，是人的肢体运动和本体反应；太极拳属于武术，是人的心理活动和对抗行为；太极拳蕴含力学原理，是人体与人体、人体与大地的相互作用，具有作用力与反作用力等力学性质。运用现代力学理论分析太极拳的技术动作，揭示太极拳“小力胜大力”、“牵动四两拨千斤”、“引进落空”等奥妙，探索一条运用现代科学理论和技术手段研究太极拳的途径，对于促进太极拳的科学化发展和国际化传播具有很强的现实意义和深远意义。

一、建立人体刚体模型以分析太极拳的力

（一）太极拳攻击力的来源

太极拳是武术的一个拳种，具有独特的技击功能和巧妙的攻击能力。太极拳的攻击力来源于三个方面：

一是源于脚与大地的接触。太极拳理论大家武禹襄（1812—1880）的《太极拳论》［1］讲：“……其根在脚，发于腿，主宰于腰，形于手指。由脚而腿而腰，总须完整一气……”这不仅讲明了力的传递过程：起自脚，发于腿，转由腰，运至手。而且强调，借助地面将下肢稳住了，上肢才能实现攻防的意向；起于下肢的力要通过躯干传达于上肢，上肢才能将力施加给对方。武禹襄之后有许多论文、专著讨论“其根在脚”的重要性和实施方法［2］［3］［4］。太极拳中的长劲就是典型运用地面反作用力攻击对方的发劲方法。［5］10-17

二是源于人体的整体动量。动量是一个力学概念，是指物体质量和速度的乘积，在太极拳中用来描述太极拳的拳劲［6］54-69。太极拳讲究“一动无有不动”，其攻击和防守是在肢体不断变化的运动中实现的，有速度、有质量，采用力学的术语是具有“动量”。正如太极拳宗师王宗岳（明代万历年间生人）在《十三势行功心解》［7］中讲：“……所谓变动虚实也，……运劲如百炼钢，……发劲如放箭，……蓄而后发，……”例如，“靠”是太极拳的近身战术，是以胸、肩、背的动量（速度乘以质量）靠击对方，威力很大。又如太极拳的“转腰”动作能够形成人体的旋转（角）动量，该旋转动量产生很大的攻击力。

三是源于相对运动形成的动量。《十三势行功心解》［7］中说：“……曲中求直，蓄而后发。力由脊发，……”。杨式太极拳宗师杨澄甫（1883—1937）在《太极拳术十要》中说“……能含胸则自能拔背，能拔背则能力由脊发，所向无敌也。”。人的腰脊质量大，手臂质量小，两者相对运动时，腰脊很小的速度可造成手臂很大的速度。太极拳令人惊叹的短劲就是由腰脊发力通过臂手打击对方［5］。

总之，力可以出自地面或者其他支撑面，攻击者将地上的正向反作力和摩擦力传递给对方；力也可出自人体的整体动量，人体的动量和对方碰撞，给对方施加冲击力；力还可以出自脊胸，大质量脊胸和手的相对运动赋予手高速度，手的动量和对方碰撞产生力。这三种力能够联合对外，是太极拳的威力所在。

（二）太极拳推手中的牛顿第三定律和人体刚体模型

太极拳的主要运动形式是套路和推手，套路是自身练功形式，也称知己功夫；推手是双人对抗训练形式（也作为两人比试功力的竞技形式），也称知彼功夫。推手训练的目的一是练习在技击对抗中如何判断对方的进攻意图（也称听劲）；二是练习如何顺势借力向对方进攻（也称发劲），其实质就是两人在身体接触的对抗中保持自身平衡，破坏对方平衡。

推手时双方以手或前臂相接触，你来我往相互施力。我方给对方施加一作用力，对方也给我方施加一个反作用力，见图1。根据牛顿第三定律这两力大小相等方向相反。并不因为某方功夫高强而能给另一方多一点力。

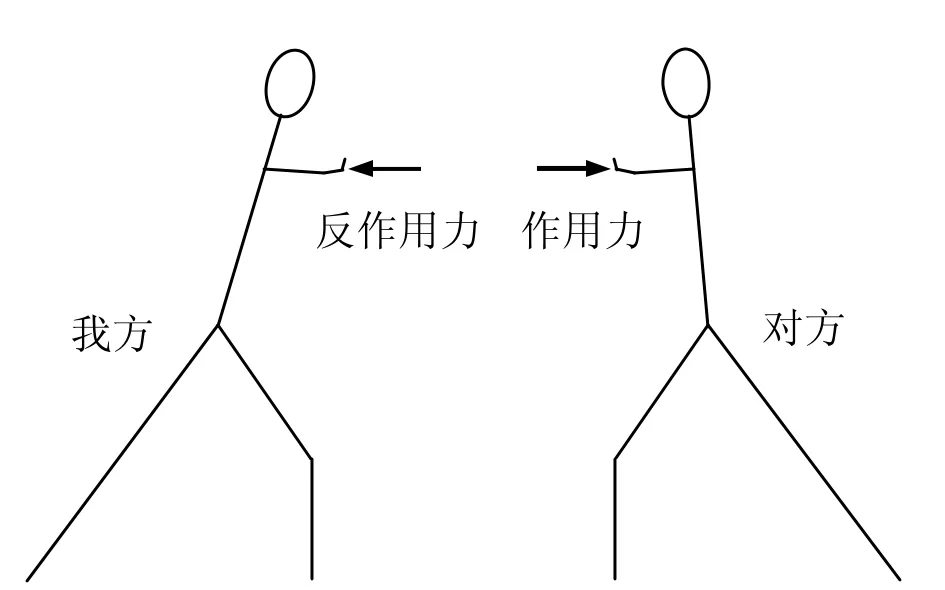
图1作用力和反作用力

用力学的原理分析太极拳可以将充满哲学理念的古老拳术与现代科学相结合，从而加深人们的理解和研究。因此，根据力学分析的一般要求和用于分析太极拳的需要，采用隔离体分析。如图2所示，把人体简化为平面内的一个刚体模型（简称为刚体），各肢体简化成刚杆，刚杆的接点视为刚性，脚和地面的接触处简化为点。人体的质心是人体质量的中心，与重心重合，质量是指人体所含物质的多少。人体的质量是m，重力是W=mg 。隔离体分析就是把一个人体与外界的因素都化成力进行人体运动状态分析。图2是我方隔离体示意图。其中：

m-人体质量

W=mg -人体重力垂直向下，作用于重心

g=9.8（m/s2）-重力加速度

F-对方对我方施加的水平外力，和我方施于对方的攻击力大小相等方向相反

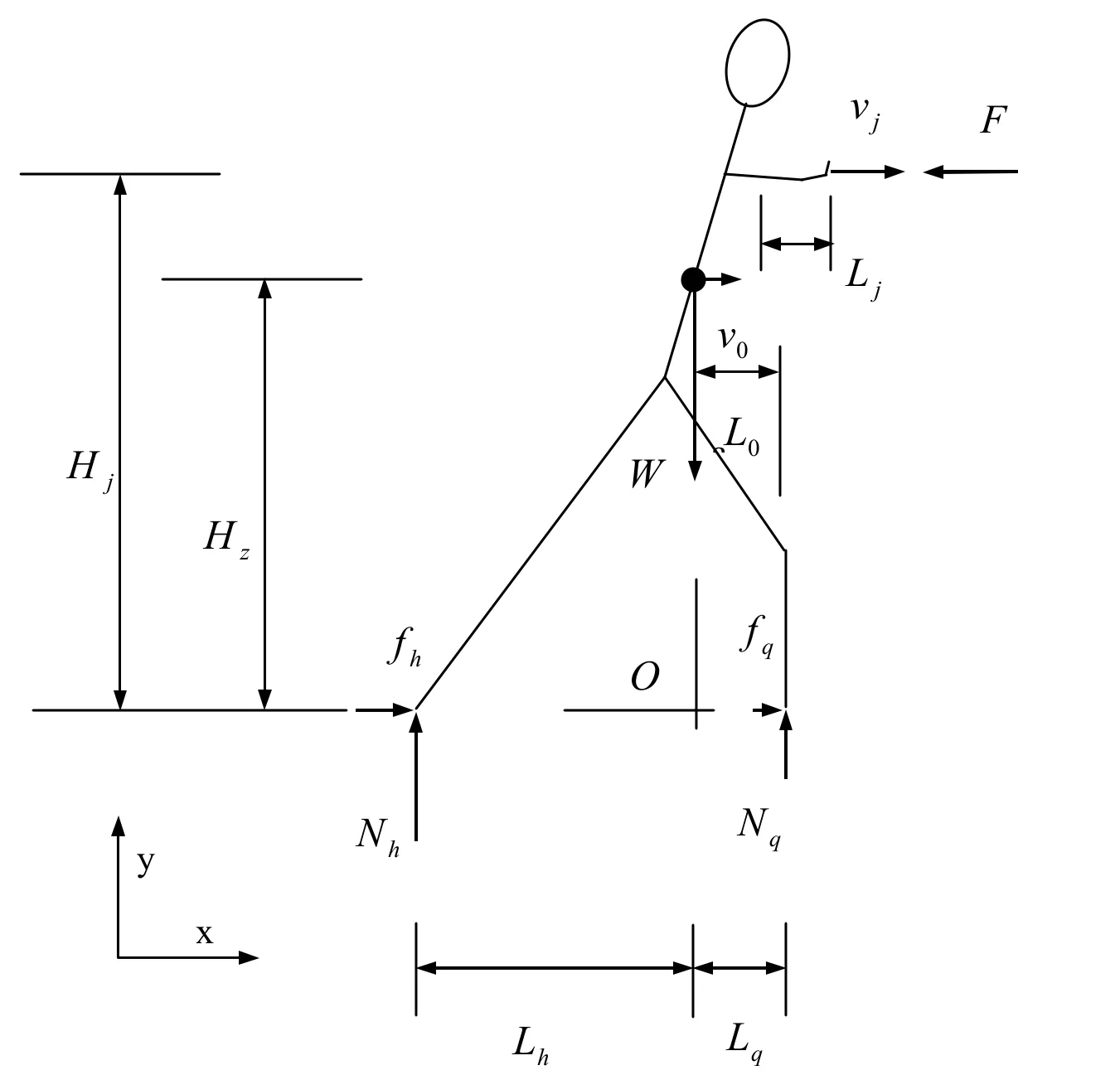
图2刚体模型的隔离体

Nq-地面对前脚的正向支撑力

Nh-地面对后脚的正向支撑力

fq-地面对前脚的切向摩擦力

fh-地面对后脚的切向摩擦力

Lq-重心到前脚的水平距离

Lh-重心到后脚的水平距离

Hz-重心到地面的高度

Hj-接手处到地面的高度

v0-人体质心的水平初速度

vj-手的水平初速度（由于手和身体的相对运动产生）

（三）太极拳人体刚体模型的力学条件

1. 摩擦力

一个物体放在水平地面上，有一个水平力Fs作用于其上，见图3-图5。地面对物体有一个与重力等值反向的正压力N，地面对物体有一个摩擦力f。

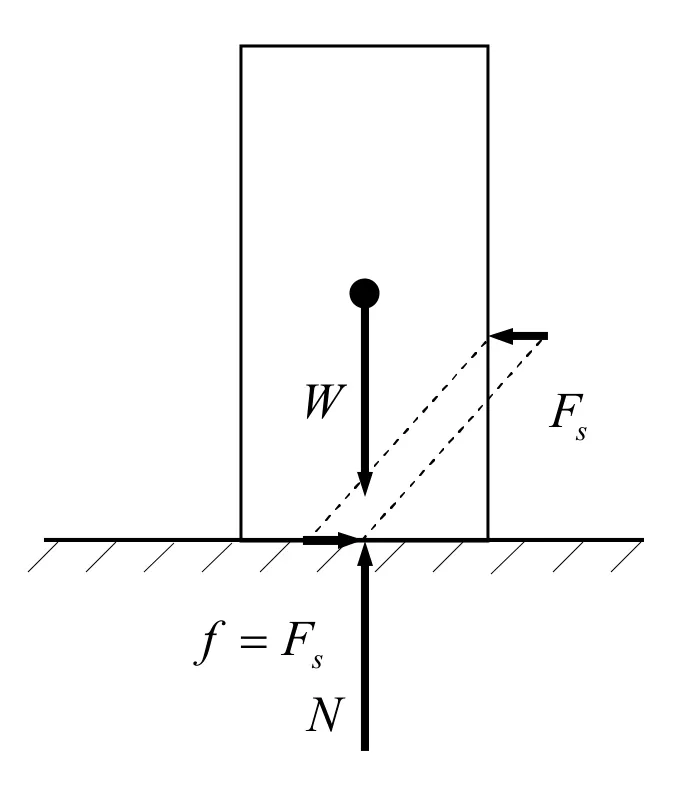
图3 水平力＜最大摩擦力

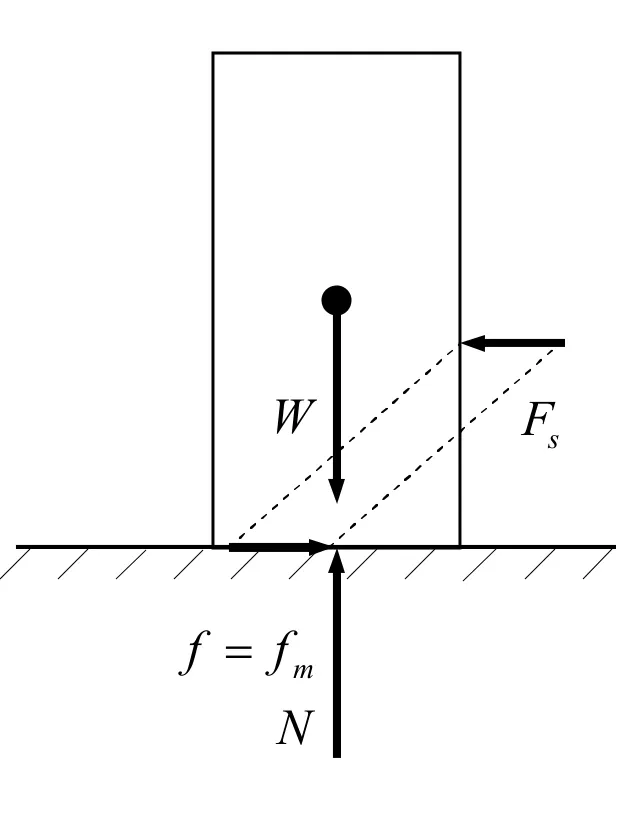
图4 水平力=最大摩擦力

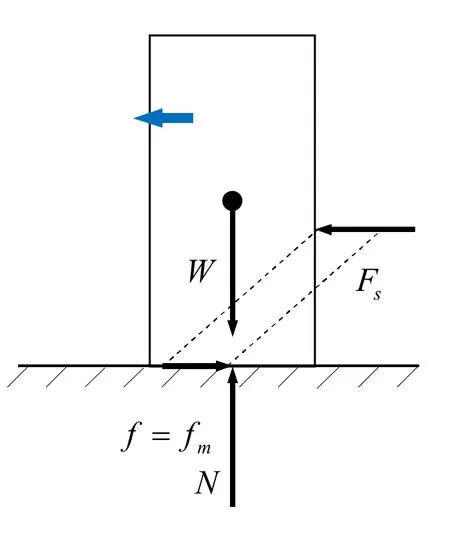
图5 水平力＞最大摩擦力

摩擦力有个上限，称为最大摩擦力fm。最大摩擦力与正向力成正比，

这里μ是摩擦系数。鉴于水平力和最大摩擦力的大小关系，有三种情况。如果水平力小于最大摩擦力，则摩擦力和水平力相等，物体不动，见图 3。如果水平力等于最大摩擦力，则摩擦力也等于最大摩擦力，物体处于要滑未滑的临界状态，见图 4。如果水平力大于最大摩擦力，则摩擦力等于最大摩擦力，物体滑动，见图 5。数学表示为，

2. 人体的平衡

以人体的重心位置变化作为依据，人体有三类平衡：稳定平衡、不稳定平衡和随遇平衡。

稳定平衡：人体在外力作用下，偏离平衡位置后，当外力撤除时，人体自然恢复平衡位置。如果物体偏离平衡位置的结果是物体重心升高，则该平衡是稳定平衡。太极拳的多数步式属稳定平衡，如弓步、虚步。

不稳定平衡：人体在外力的作用下，偏离平衡位置后，当外力撤除时，人体不仅不能回到原来的平衡位置，而是更加偏离平衡位置。如果物体偏离平衡位置的结果是物体重心降低，则该平衡是不稳定平衡。如果把脚与地的接触面简化成一个点的话，太极拳中的单腿独立式属不稳定平衡。

随遇平衡：人体在外力的作用下，偏离平衡位置后，当外力撤除时，人体既不回到原来的平衡位置，也不继续偏离原位置，而是在新位置上保持平衡。随遇平衡在太极拳运动中很少见。

人体平衡的一般条件是重心的垂线与地面的交点在支撑面内，并且要有一定的稳定角。地面为人体提供了向上的支撑力，两脚或单脚与地面的接触面是支撑点，身体向地面的投影构成了支撑面，重力作用线同连接重心与支撑面边缘相应边界的直线二者之间的夹角构成了稳定角，见图6。随时保持自我平衡是太极拳的重要目标，不仅要做到平衡，而且要追求平衡的稳定程度。因此，人们在习练太极拳时都非常注意把重心保持在支撑面内和增大稳定角，以有利于增强身体自我的平衡性和稳定性。

重心越低，支撑面边界越远，稳定角越大。稳定角越大，稳定性越好；稳定角越小，稳定性越差；稳定角为零，人体处于临界状态。

太极拳身形中，弓步、虚步的稳定角都有较大量值，稳定度都很好。相比而言，弓步前后脚的稳定角都很大，而虚步后脚的稳定角偏小，所以弓步比虚步的稳定性要好。

单腿独立一类的身形稳定角都较小，因而稳定度低，尤其在脚宽方向最差。如图7的金鸡独立一式，重心高约100cm，稳定角不到3度，因为脚宽的一半一般不超过5cm。这样的姿势常被作为训练身体稳定性的桩功，通过练习调节脚底压力分布和肢体位置的能力，提高重心和压力中心对齐的程度。

从运动学讲，太极拳是一种人体平衡运动，是在锻炼保持自身平衡同时破坏对方平衡的能力。套路训练是用于增强自我平衡能力，推手训练是用于增强破坏对方平衡能力，两者都是训练人体在一定速度下重心在相应支撑面内移动的能力。人体有速度时，重心在支撑面内移动是动态平衡；人体速度为零时，重心在支撑面内移动是静态平衡。太极拳套路训练要求在转变动作过程中和定式时都要平衡，其实质就是要实现动态平衡和静态平衡。在推手中，我方要在发放中和发放完的所有时刻都是平衡状态，而对方在被发放过程中，前期处于动态平衡状态，后期就处于不平衡状态。对方因被发放而倒地或跳出都是身体失去平衡的结果。

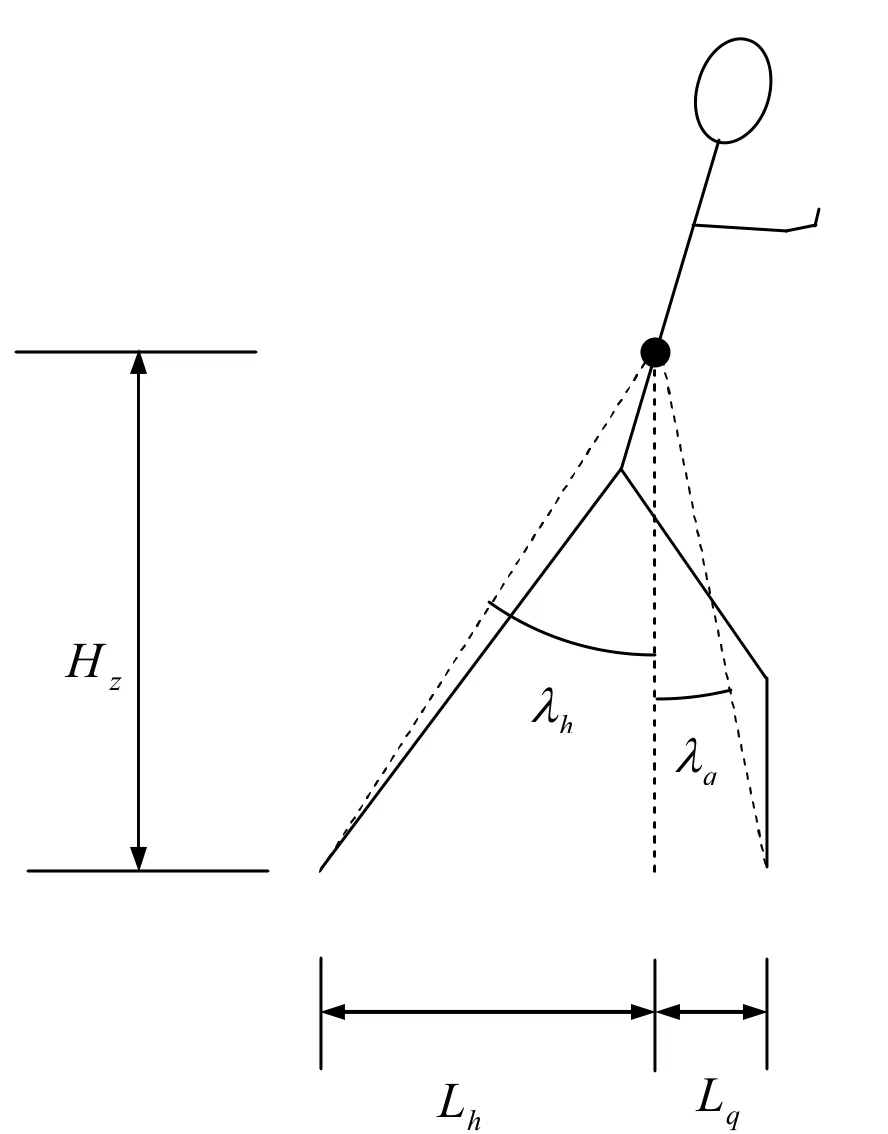
图6稳定角

图7独立的稳定角

在推手时，当我方重心越出支撑面一点点时，如果对方有一个顶的动量或力作用于我方，我方仍会保持平衡，处于稳定状态；如果对方是个太极高手，不但不顶，却顺势拉我方一下，那我方的重心会越出支撑面更远，再也无法找回平衡。因此，任何时候都要避免让重心越出支撑面。

3. 动量传递

动量是质量和速度的乘积，两个动量可以通过碰撞相互传递。这可以从对两个质点（是指只计质量忽略不计大小、形状的物体）弹性碰撞的分析中看出。碰撞前两质点有各自的速度，碰撞后他们的速度是什么？设：

m1-质点1的质量

m2-质点2的质量

v10-质点1碰撞前的速度

v20-质点2碰撞前的速度

v1-质点1碰撞后的速度

v2-质点2碰撞后的速度

按照动量守恒原理，碰撞前后的总动量不变，即：

弹性碰撞时动能守恒，即：

由（3-4）解得：

由此可见碰撞使两质点的速度得到了改变。把（3）式改写为：

（6）式左端是质点1动量的改变，右端是质点2动量改变的负值，（6）也可解释成质点1将一部分动量传递给了质点2，而质点2将等量反向的动量传递给了质点1。所以动量可以通过碰撞传递，而且这传递是互相的。我们都熟悉两个悬挂着的等质量弹性小球相互撞击的物理实验，这是一个典型的动量传递实验。小球A以一定速度撞击静止的小球B，撞击后，小球A停住，而小球B等速上摆。小球B摆回后撞击已经静止的小球A，撞击后，小球B停住，而小球A等速上摆。

动能在碰撞时也有了传递，但动能传递和动量传递遵循不同的规律。动量传递有方向有大小，是矢量运算。动能传递只有大小，是标量运算。动量守恒（3）适用于弹性和非弹性碰撞。动能守恒（4）只适用于弹性碰撞。在非弹性碰撞中一部分能量转换为非动能的形式，（4）的右端小于左端。由于上述两个原因，动量传递更适合于描述碰撞。

太极拳的推手在力学上可以认为是碰撞。因而我方有一部分动量传给对方，而对方有一个大小相等方向相反的动量传给我方。

4. 动量传递时的冲击力

动量是质量和速度的乘积。质量是个标量；速度有大小有方向，是个矢量。标量和矢量的乘积还是矢量。因动量是质量和速度的乘积，所以物体的动量是：

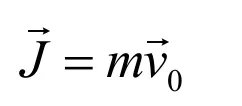
物体与另一物体碰撞需要一定的时间，在此段时间内的平均加速度为速度的变化除以碰撞时间：

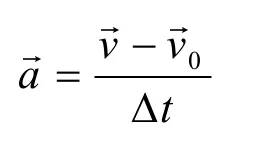
按照牛顿第二定律力是质量和加速度的乘积，因而物体受到的冲力为:

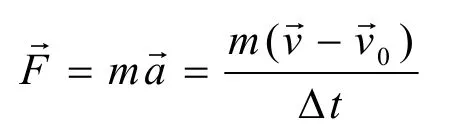
由上式可见冲击力和速度差成正比，和质量成正比，和碰撞时间成反比。平均冲量为：

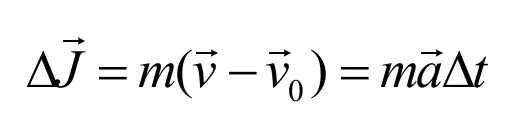
我方质心初速度为v0，见图二。当我方完成攻击时仍然要平稳，所需条件是重心没越过前脚时速度为零。假设质心作匀减速运动，由（7）式得：

其中ap是平均加速度。设在路程中速度减为为零。从运动学角度讲，物体在路程L0上作匀减速运动时有：

解（8-9）我们得到距离、初速度和平均加速度的下式关系：

在太极拳推手中，当我方用手（或其他肢体）攻击对方时，通常是由“曲蓄”而“直发”。这时在手和上体之间有一个相对运动，其原理与炮击相类似都遵循了动量守恒原理。炮击时，炸药爆炸产生的强大动能使原来没有速度的炮弹和炮身同时获得动量，炮弹获得一个向前的动量，炮身获得一个等量反向的动量。因炮弹的质量远小于炮身的质量，所以炮弹高速向前，炮身低速向后。同理，推手是人体肌肉放能，手因质量小而快速向前，脚以上身体其余部分因质量大而低速向后。

由此，假设手的初速度是vj，手运动的距离是Lj，手的平均加速度是aj，于是，类似于（10）得下式：

本文假设手的质量是mj，手的相对运动产生的攻击力为mjaj。这里手的质量是个模糊概念。因为手在向前运动时并没有完全和上体隔离，其数值难以精准确定。

二、人体动力学分析

（一）人体平衡与运动的动力学条件

按照人体的平衡和运动应满足动力学定律和方程的要求，先对我方隔离体作力学分析。如图2所示，将人体简化为一个平面刚体，将所有外在因素简化为外力。这样：

在垂直方向，诸力平衡：

在水平方向，由牛顿第二定律得：

将牛顿第二定律运用于转动，引申出转动定律：刚体所受的对于某定轴的合力矩等于刚体对此定轴的转动惯量与刚体的角加速度的乘积。图2中重力线与地面的交点是O，取定轴为通过O点垂直于纸面的直线。水平力和力高Hj形成的力矩逆时针；前脚支撑力Nq和前脚距离Lq形成的力矩逆时针；后脚支撑力Nh和后脚距离Lh形成的力矩顺时针。加速度ap向左，角加速度逆时针。人体的转动惯量是将这些条件代入转动定律，我们得到：

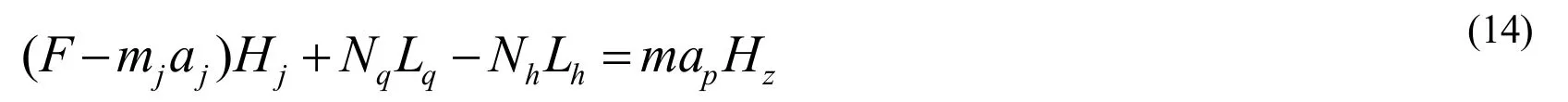
将（13）代入（14）并作一些组合，，得出：

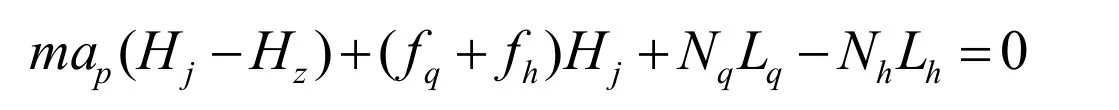
其中mpa是使质心减速需要的力，由于质心和接手有一个高度差第1项可以看成是质心减速力对高度差形成的力矩，简称为质心力矩；第2项是摩擦力对接手高度的力矩；第3、4项是正压力对质心的力矩。这些力矩共同作用达到人体动力平衡。由此可见质心力矩将对摩擦力和正压力的分配产生影响。通常接手和质心的高度差不是很大，所以对诸力的影响也不是很大，当接手和质心高度相等时该力矩消失。由公式（14）中质心力矩和前脚力矩同号，可以推断出质心力矩的存在能够减小前脚的压力。但这将使前脚失根临界条件提前发生，下面的算例也证实了这一点。为了减小这个负面影响，太极拳要求无论是习练还是实战都要做到沉肩垂肘，不要让接手处和重心有太大的高差。

上式中使手减速的力mjaj并不出现，因而该力对正压力和摩擦力的分配没有影响。下面的算例也证实这一点。

解方程组（12-14）得：

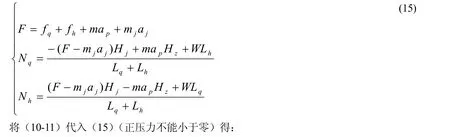
由（16）式第一式可知，我方给对方的攻击力由三部分组成：摩擦力、整体的冲撞力和后助冲撞力。

整体运动的动量和对方碰撞能够形成对对方的冲击力，并将一部分动量传给对方。质心的运动靠脚底的摩擦力来加速，通过加速积累成速度，而使整体具有动量。因而整体的冲撞力仍然来自于脚底，符合《太极拳论》中“……其根在脚，发于腿……”的论述。但是动量积累后有其独立性。设想突然将摩擦力撤走，该动量仍然会和对方碰撞而产生冲击力。这里要说明的是冲击力和直接传递来的力的瞬间效果是不同的。

手的动量和对方碰撞也形成对对方的冲击力，也将一部分动量传给对方。手的动量是靠上体的后助形成的，符合“……曲中求直，蓄而后发。力由脊发，……”的论述。我方可以力由脊发、力由腰发、力由胯发，等等。和对方接触的可以是手、臂、肘、肩、胸、背等等。这种碰撞力发自于肢体间的相对运动，和地面对脚的摩擦力没有直接的关系。为产生这种冲击力需要把全身练成一个弹性体，全身各部位都应有收缩和反弹的功能。用拳论的语言是全身各部位都应有蓄发功能。

上述分析表明了太极拳运动中三种力的力学成因。一是起于脚底的力需要通过身体各部位的接力，传递到攻击肢体，所有中间部位都要能够保持相对固定的形状，不能垮下。这是一种整劲是全身的功夫，练桩功对此很有帮助。二是整体冲撞力的酿成要靠全身运动来造就质心的速度。三是后助冲撞力的生成需要全身各部位的相对运动来造成攻击肢体的速度。这三种力都来自全身功夫，这是太极拳全身运动的力学证明。

在太极拳运动的力学分析中，《太极拳发劲的动量转递解析》一文［6］54-69将劲定义为动量， 并将劲法定义为：人体动量的有效合成与使用。本文将内劲定义为：人体动量的合成与力的传递功能。将发劲定义为：改变人体的动量。文中还研究指出，动量是通过内力加速肢体来实现的。［6］54-69见图8，想象把腿分成很多段，在假象断面处有内力作用。这里称其为内力是因为我们把人体作为研究的体系，而内力是体系内部的力。外部对体系的作用就称为外力。如图8所示，摩擦力是外力；内力1、内力2和内力3是内力。作用于脚上端的内力1和作用于小腿下端的内力大小相等方向相反。这样如果我们研究脚和小腿的组合物时，内力1就不用表述出来。

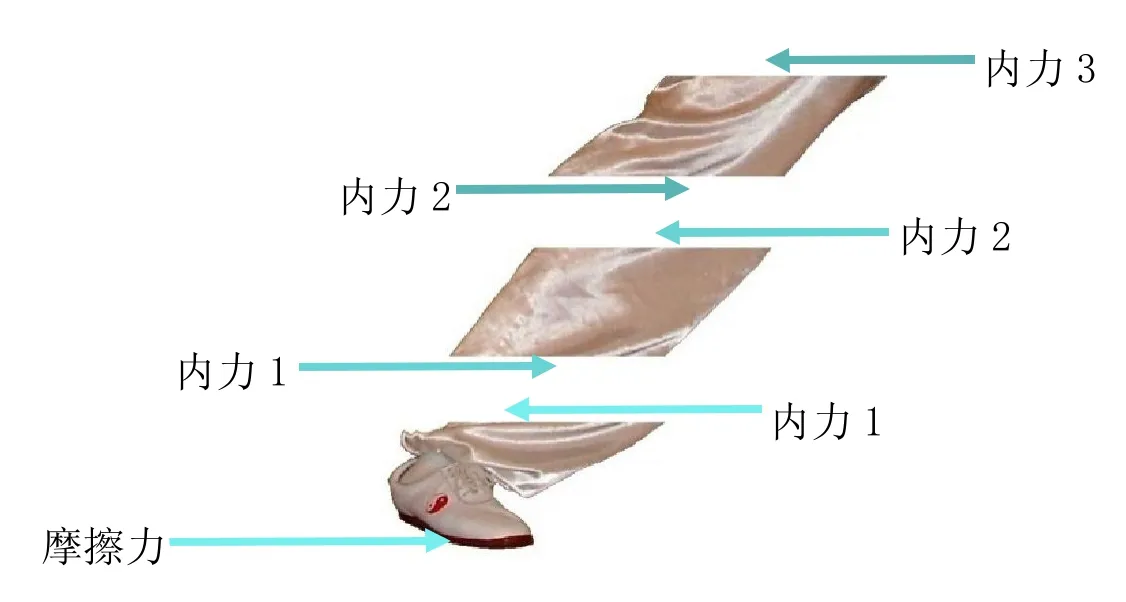
图8 肢体隔离体

人通过食物和呼吸获取营养，合成为化学能量，进而转换成肌肉的机械能。太极拳运动中的发劲主要是指通过肌肉发放机械能，也称放能。放能产生内力，图8中内力1和内力2使小腿加速，因而形成动量。如果内力1大于内力 2，小腿将获得前倾的加速度。所以内力是媒介，而力的传递是通过内力的接续来实现的。在特殊情况下，人体静止，小腿没有运动，这时内力1和内力2大小相等方向相反。也可以说内力1传递到内力2，而内力2将继续向前传。可见，力的传递在人体静止时仍然存在，当然，人体加速时力的传递也存在。小腿下端的内力1的一部分传递到小腿上端变成了膝部下端的内力2，另一部分用来加速。

发劲与有劲不同，发劲是指要改变人的运动状态，也即改变人体的动量（本文已经把劲定义为动量），要通过一定的方法。例如，太极拳讲究的中掤、捋、挤、按、採、挒、肘、靠等八种劲法，就是发劲的具体方法。而有劲是指人有一定抗拒外力或推拉重物的力量，不一定和动量积累有关。例如有的人被推拉时不为所动，能够与对方处于对抗状态，这是一种有劲的表现。因为双方基本是一种静止状态，没有位移和速度变化，也不像太极推手那样用化解的技法抵抗住对方的攻击。要能抗住对方的推力需要有两个条件：其一是人体要能够保持形状，力学上把人体简化成刚体；其二是人体的隔离体分析要符合力学平衡条件。

（二）脚底打滑的临界条件

脚底打滑是习练太极拳的大忌，不但影响自身技术水平发挥，而且极易成为对方攻击的机会。防止脚底打滑，即做到脚底不打滑的必要条件是水平外力不能大于摩擦力的最大值，见（2）式。这个条件也可表述为：水平力和正压力的合力线要在摩擦角内。摩擦角θ的定义是：摩擦角的正切是最大摩擦力和正压力之比，该正切等于摩擦系数。以前脚为例，见图9—图11：

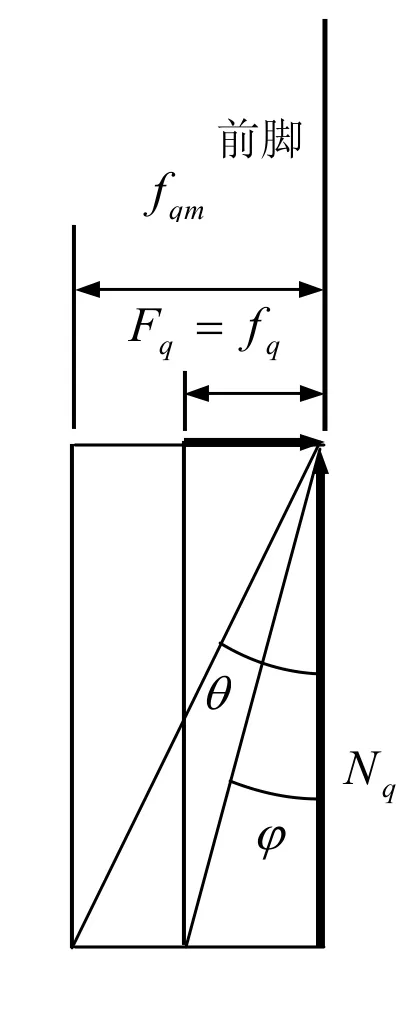
图9 力线角＜摩擦角

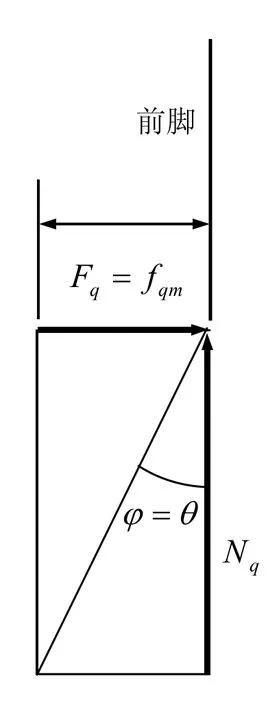
图10 力线角=摩擦角

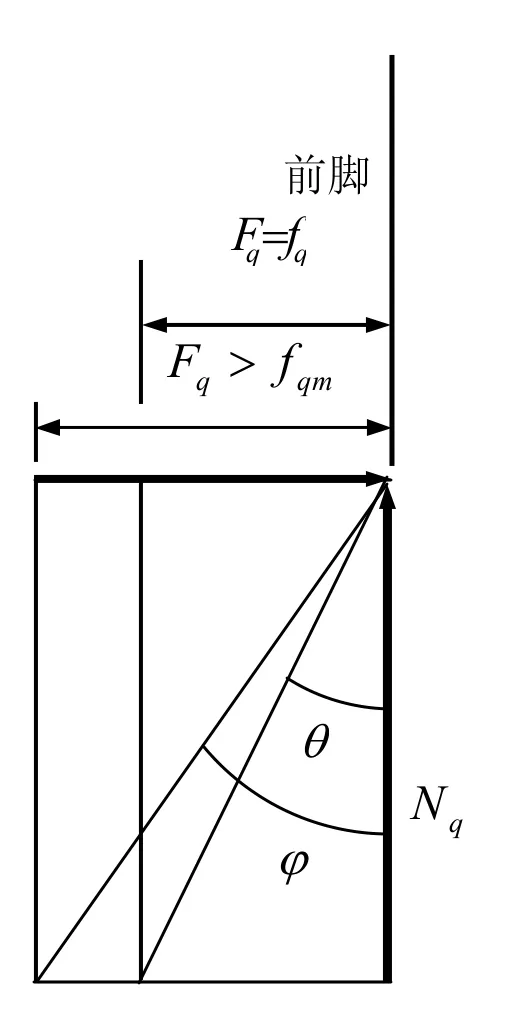
图11力线角＞摩擦角

式中 fqm是最大摩擦力。

力线角φ的定义：力线角的正切是水平力和正压力比，即：

因此，打滑的临界条件是：

图9和图3对应，符合条件φ＜θ，不打滑。图10和图4对应，符合条件φ=θ，临界。图11和图5对应，符合条件φ＞θ，打滑。

摩擦角和腿的方向没有直接关系。腿（其他肢体也一样）能承受纵向力和切向力，所以能传递和腿纵向不同的力。

上面的讨论对后脚也成立。而且前后脚的力线角是一样的。即：

如果一只脚的支撑力为零，则重力完全由另一只脚承担。如果一只脚的摩擦力为零，摩擦力也完全由另一只脚承担。这样，将（20）式代入（12）式（力线角的和摩擦角都用正切定义），得：

由方程（21）可知，两脚的摩擦力之和必需小于重力和摩擦系数的乘积时脚才能不动。由此我们得出脚底不打滑条件：水平外力不能大于总摩擦力的最大值。

（21）还说明总摩擦力和重力成正比。重力越大，摩擦力也越大，可提供更多水平攻击力。重力还将力线角变小，进一步减小打滑的机会。所以大个子在推手中占优势。

上述公式讨论的是静摩擦状态下的脚底打滑临界条件。一旦超过这个临界条件，脚就会相对于地面打滑。一旦打滑，就进入了滑动摩擦状态。一般情况下，滑动摩擦系数小于静摩擦系数，即进入滑动状态时会突然失去一部分摩擦力而加速打滑状态。所以打滑的可逆性差，打滑可能最终导致失稳。

将（21）（10）（11）式代入 （13）式，得：

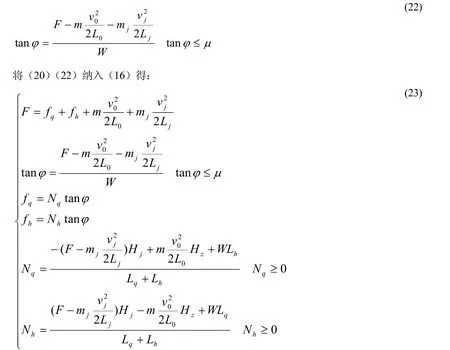
需要注意的是，摩擦角和平衡角是完全不同的概念。摩擦角阐述了摩擦力的性质及其在传力中的地位，平衡角定义了重心和支撑面的关系。

令（23）第2式中力线角等于摩擦角，可以得到打滑的临界条件：

（三）失根的临界条件

失根是太极拳的一个用语，始于脚底腾空，这时脚底正压力为零，是人体失稳的先兆。在太极拳推手中，往往是谁先失根谁就失败。为了有效控制失根，太极拳在训练和竞技中采取了许多方法和措施，从力学的角度讲，就是要保证任何一只脚的支撑力不能是负值。

（23）是用于推导人体平衡和运动的动力学条件及其相互关系，设水平外力为零、人体速度为零，则（23）式变为：

（25）式中，因为没有水平外力，摩擦力也不复存在。（1）式是最大摩擦力的计算公式。脚底摩擦力随着承重量大小变化，并于水平外力密切相关，但不超过（1）的量值。比较（23）第5式和（25）第5式可以看出水平外力将减小前脚的承重量；比较（23）第6式和（25）第6式可以看出水平外力将增加后脚的承重量；由（25）第5和第6式可见，没有水平力时，两脚的承重量和两脚到重心的水平距离成反比。如果水平外力从零开始增加，则前脚的承重量逐渐减小，后脚的承重量逐渐增加，两脚底都有了摩擦力。当前脚的承重量减小为零时，前脚支撑力Nq也为零，前脚也就不再得到地面的支撑，处于失根的临界状态。如果此时将前脚提起，把精力集中在后脚上，就会致使前脚失根。令（23）第5式右端为零，我们得到失根的临界条件：

如果水平外力是拉力的话，后脚的支撑力会随外力增加而减小，当后脚支撑力为零后会导致人体失稳。为保证人体的基本稳定，在（23）式第5和第6式中设了限制条件，也得出了保证脚底有根的条件：任何一只脚的支撑力不能是负值。

太极拳对脚与地面的接触非常讲究，尤其要求脚落地要生根。从力学上讲，脚和地面之间的相互作用力就是根，有作用力就有根，作用力大根就牢，作用小根就差，作用力为零时根就消失了。

（26）式表明推手时双方接手部位越高，重心离后脚越近，前脚就越容易脱地，以至形成失根临界状态。这种临界状态并不代表人体已经失稳，因为这时还有水平外力（对方在接手处的力）的存在，所以人体仍然处于平衡状态。但是，这种临界状态极易给对方造成进攻机会，易被对方引进落空。一是对方突然撤力，水平外力为零，假如我方毫无思想准备，前脚极易在惯性作用下骤然落地，处理不当会屈曲前腿而失稳。二是对方施加一个反向水平力，那我方的平衡将处于危机状态。

因此，太极拳要求前脚在支撑力为零的情况下，一般不要离地，以有效遏制对方的引进落空战术。如果对方突然撤力，我方因前脚从来没离开地面而可随即获回支撑力。如果对方施加反向水平力，我方也因此可以随即获回支撑力而应对自如。

当水平外力超（26）式的临界值，该水平外力对后脚的力矩大于重力对后脚的力矩，人的上体将首先被合力矩向后掀，人的重心也随之被向后推，如果重心被推到后脚的后面，整个身体将失稳，甚至倒地，见图 12。采取身体前移、降低重心、增大支撑面和稳定角等措施可以防止或缓解这种状态的出现。推手出现顶牛状态时，双方做出的弯腰、下蹲、两脚前后拉开、伸远后脚的动作就是这些措施的具体运用。

一般情况下，这些应对措施仅在双方体重相差不大时才有效。因为一方给另一方的水平力均来自对方的摩擦力，而这个摩擦力又是在相同摩擦系数下和重量成正比。

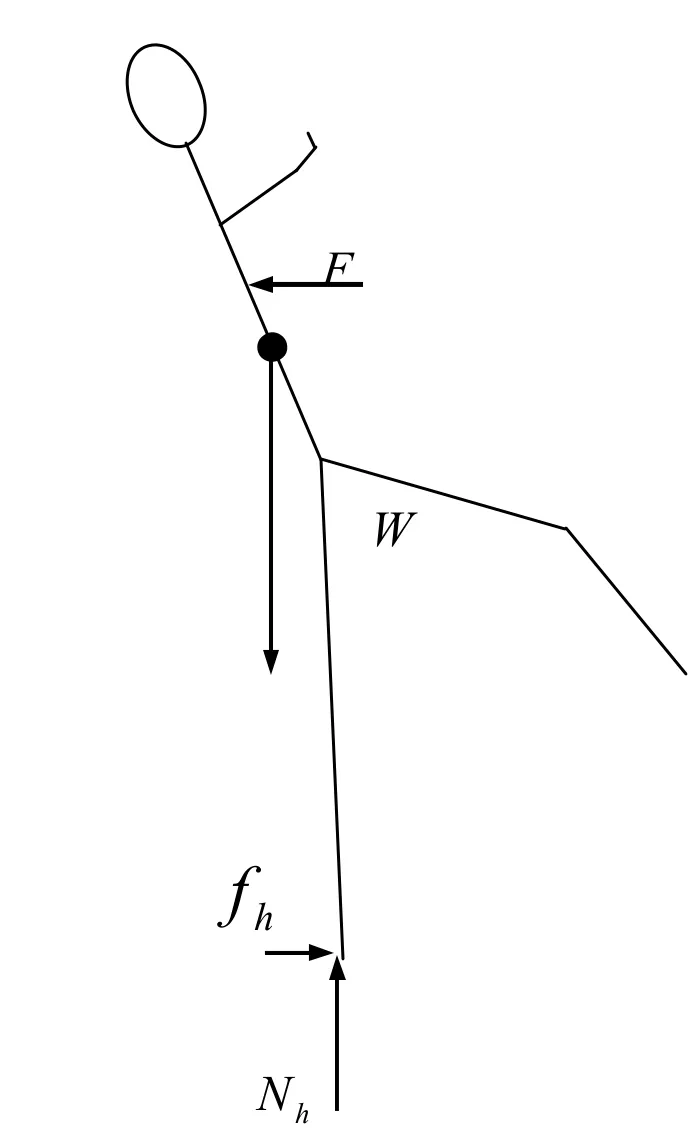
图12 最终失稳

三、弓步的水平攻击力计算与分析

（一）只有传递力的特例

弓步是太极拳中最常见和最常用的步形，弓步的水平攻击力直接影响太极拳推手的质量。我们先用前文推导出的打滑临界条件公式和失根临界条件公式，计算弓步在躯干和手都没有速度情况下的传递力和攻击力的性能。

将（30）假设的弓步数据分别代入公式（27）、（28）、（29）计算出弓步时各力及力线角随水平外力的变化（表一、图13）。

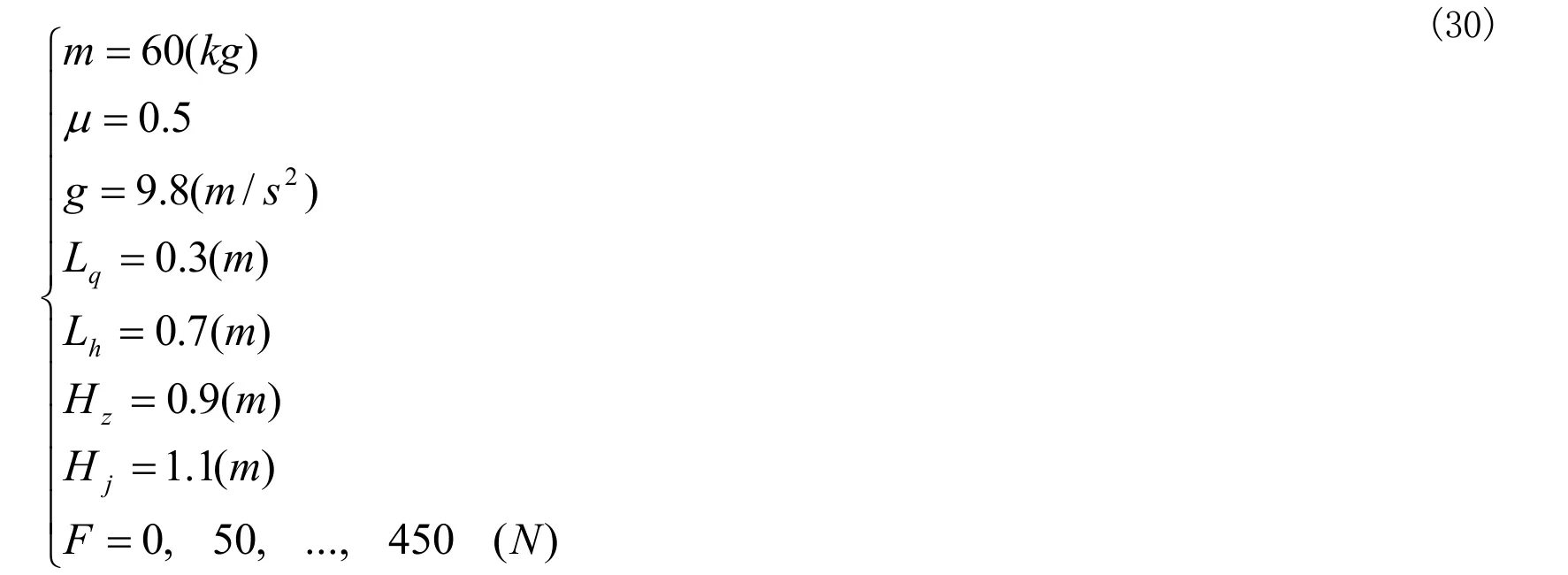
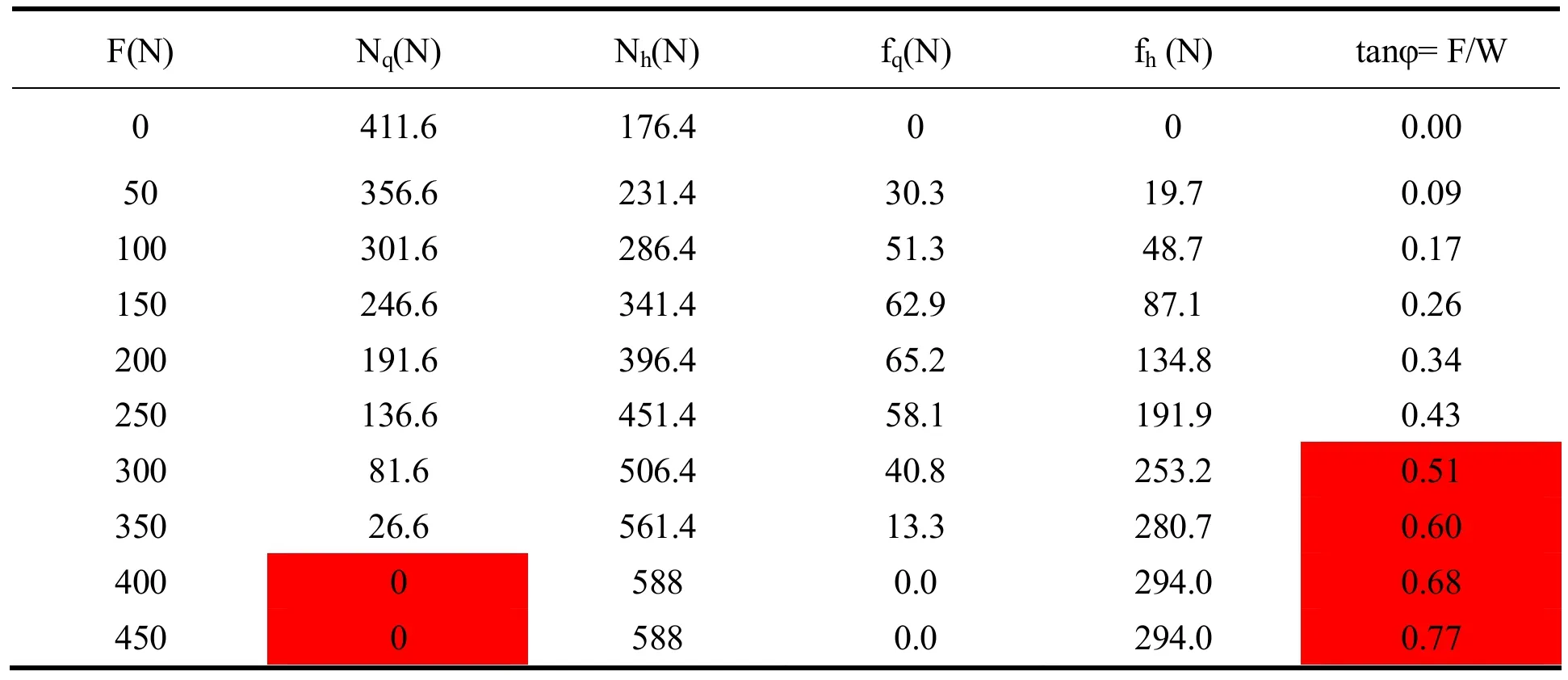
表1 弓步时各力及力线角随水平外力的变化

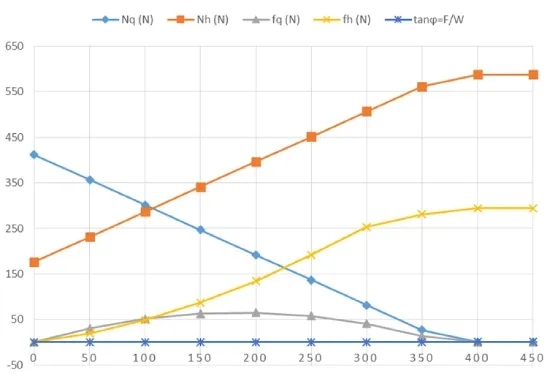
图13 各力随水平外力的变化曲线

表1分析：由第1栏和第2栏可见前脚正压力随水平外力增加而减小，用（29）式计算可知，当水平外力为374.2时正压力变成零，这是失根的临界点。由第一栏和第6栏可见力线角随水平外力增加而增加，用（28）式计算可知，当水平外力为294时力线角等于摩擦角，这是打滑的临界点。由上述可知，弓步在只有传递力的情况下脚底打滑先于失根，所以该弓步将以打滑而失效。

图13是各力随水平外力的变化的曲线。水平轴是水平外力，单位是牛顿（N）；竖直轴是各力的数值，单位也是牛顿（N）。

图13分析：当力线角增至摩擦角后（tanφ≥μ），水平力将大于摩擦力。摩擦力等于正压力和摩擦系数的乘积。（27）变为：

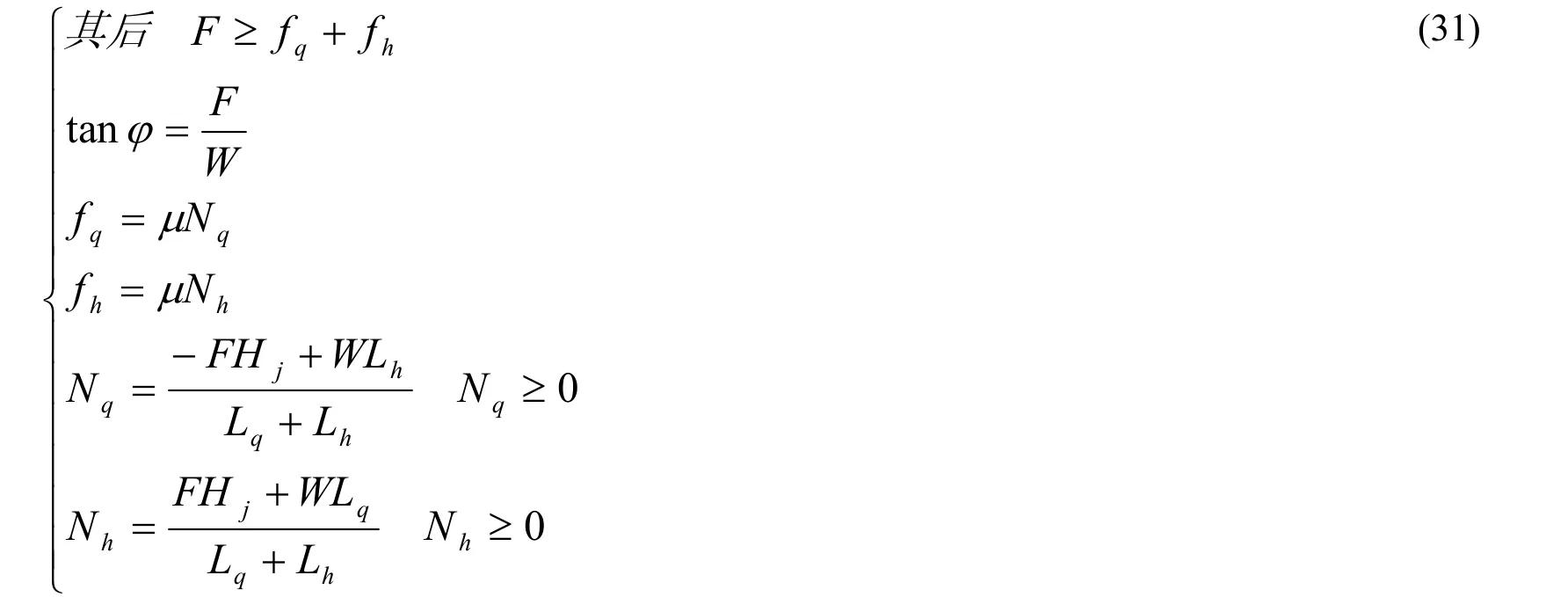
（31）式第1式是说，水平外力大于摩擦力的部分将使人体加速而滑动，加速使人体最终滑出赛场。用（31）式计算表一中自F=300N 以下各行（至下一个临界条件）。当前脚正压力递减至零时，后脚正压力递增至588牛顿。之后，当水平力大于（29）式右端后，两脚正压力不变，后脚承担全部摩擦力的最大值，（31）式就变为：

（32）式第1式是说，水平外力和其高度的力矩大于重力和后脚距离的力矩，力矩的差值将使人体加速，直至被掀翻。

用（32）式计算表一中自F=400N 以下各行。可见，前脚摩擦力增至峰值后递减，当该脚正压力为零后摩擦力也为零，此时后脚摩擦力增至294N后保值不变。294N就是全部由重力产生的摩擦力，等于重力和摩擦系数的乘积。

（二）人体动量的撞击力对弓步攻击力的影响

太极拳是“一动俱动、一到全到”的全身运动，正如太极拳论所说“其根在脚，发于腿，主宰于腰，形于手指，由脚而腿而腰，总须完整一气”。人体的刚体模型给出了这种运动的力学基础。太极拳“一动俱动、一到全到”的技术要求是对人体动量的合理使用，就是要求人体各部位能够做到协调联动和同时到位。

人体的整体动量通常称为人体动量，主要是指平动动量和角动量（旋转动量）的综合效应。在太极拳中腰主转动，造成整体的角动量；腿推动上体，造成整体的平动动量。这两者构成人体的整体动量，能够产生很大的冲击力。

为简化计算，本文把人体动量表示为人体质量和质心速度的乘积。太极拳“一动俱动、一到全到”的技术要求，就是要求人体各部位能够做到协调联动和同时到位。这是对人体动量的合理使用。

设质心有一初速度v0，手没有速度，将代入（23）（24）（26）得：

（36）假设的弓步数据加入了质心的参数，将其分别代入公式（33）、（34）、（35）得出弓步时人体动量撞击力对攻击力的影响（表二、图14）。

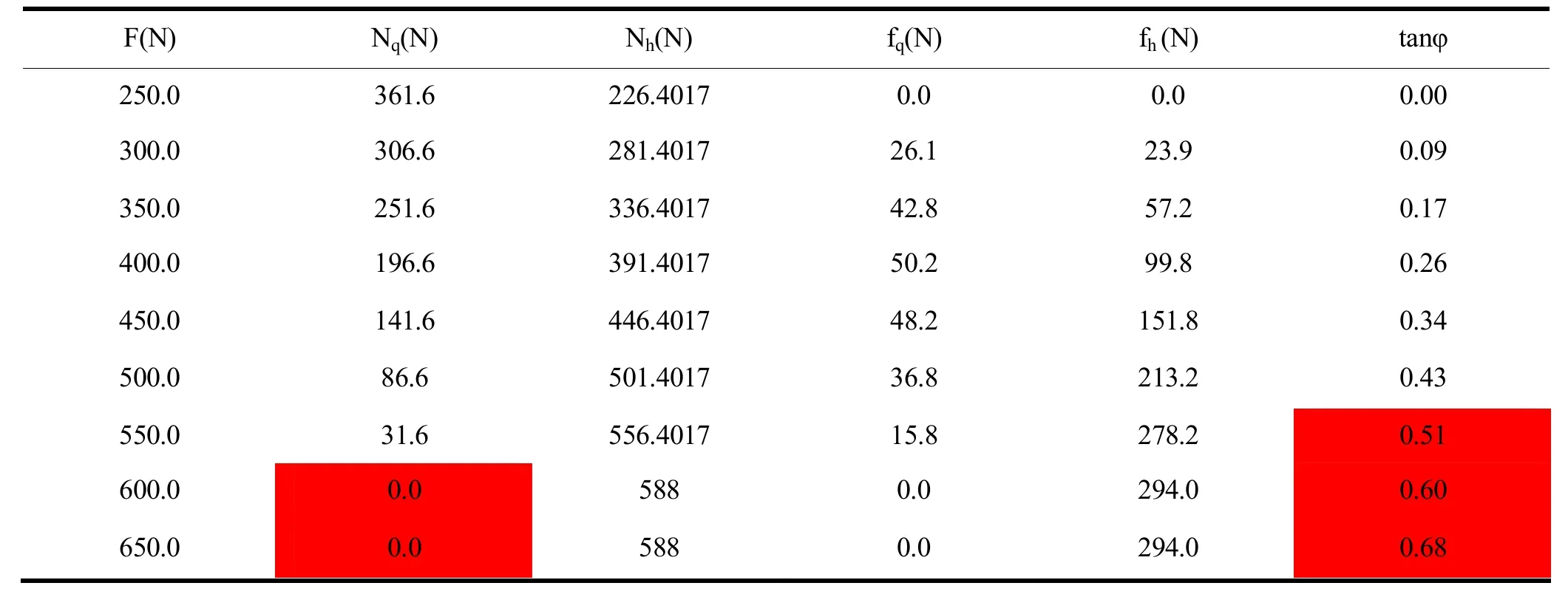
表2 弓步时人体动量撞击力对攻击力的影响

表2分析：由第1栏和第2栏可见前脚正压力随水平外力增加而减小，用（35）式计算，水平外力是为578.7时正压力变成零，这是失根的临界点。由第1栏和第6栏可见力线角随水平外力增加而增加，用（34）式计算，当水平外力为544时力线角等于摩擦角，这是打滑的临界点。由上述可知，带有撞击力的弓步在人体动量作用下，相比较只有传递力的弓步，虽然提高了250牛顿的攻击力，也缩小了打滑与失根时水平外力的差，但仍然是打滑先于失根，所以该弓步将以打滑而失效。

图14是引入质心冲击力后各力随水平外力的变化的曲线。水平轴是水平外力， 单位是牛顿（N）。竖直轴是各力的数值，单位也是牛顿（N）。

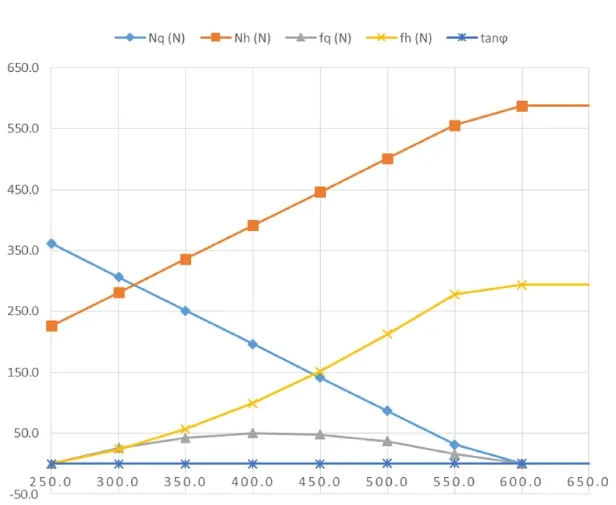
图14 引入质心冲击力后各力随水平外力的变化曲线

图14分析：将图14与图13比较，图14的曲线大致地向右拓展了250牛顿。这250牛顿就是引入质心冲击力的结果。也就是说，运用全身的质心运动使弓步的总攻击力增加了250牛顿。值得注意的是，由于引入了质心冲击力，就有了质心力矩的存在，这就致使前脚相比只有传递力时提前失根（表一失根临界点是374.2牛顿，表二失根临界点是578.7，如果减去质心冲击力250牛顿，仅为328.2牛顿）。

当力线角增至摩擦角后，摩擦力等于正压力和摩擦系数的乘积，（33）式就变为：

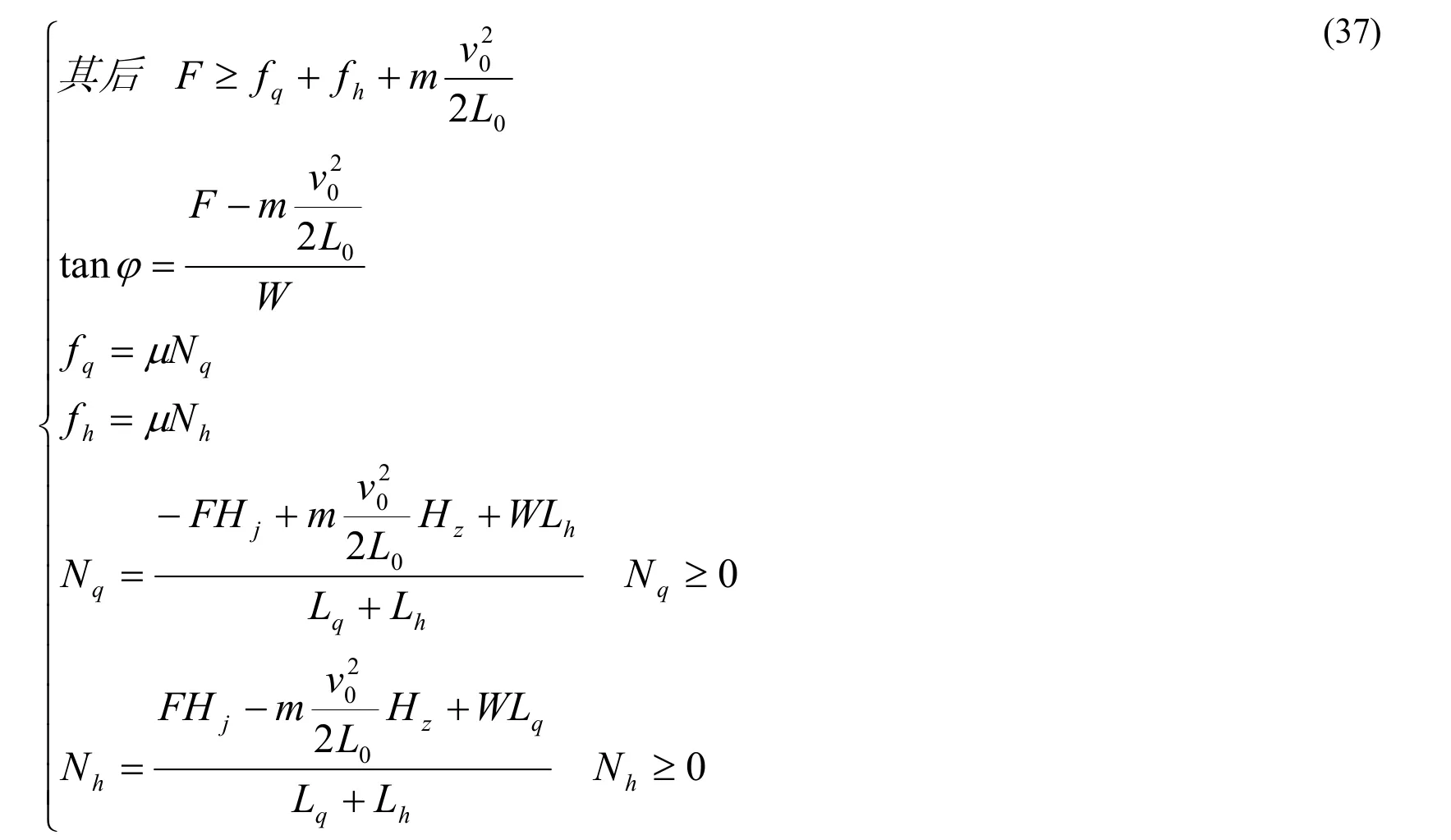
用（37）式计算表二中自F=550N以下各行（至下一个临界条件）。可知，当水平外力等于（34）式右端时前脚正压力递减至零，后脚正压力递增至588牛顿。588牛顿正好是重力的全部。其后，当水平外力大于（34）式右端时，（37）式就变为：

用（38）式计算表二中自F=600N以下各行。可知，前脚摩擦力增至峰值后递减，当该脚正压力为零后摩擦力也为零，此时后脚摩擦力增至294N后保值不变 。294N就是全部由重力产生的摩擦力，等于重力和摩擦系数的乘积。

（三）爆发力对弓步攻击力的影响

前面讨论了人体整体运动对攻击力的影响，这里将讨论肢体末梢的运动对攻击力的影响。（23）式中第一式第4项是手的综合动量造成的冲击力。我们知道，肌肉放能可以使手和躯体间产生相对运动，躯体和手同时获得等量反向的动量增量。因为躯体质量大手质量小，所以躯体的速度低，手的速度高。高速运动的手会给对方造成很大的冲击力，太极拳界称此为短劲［5］或“鞭梢劲儿”。在拳论中称此为“……行于手指……”，本文称为爆发力或肢体相对动量。为简化计算，本文把肢体相对动量表示为手的质量和速度的乘积。

设手有一个初速度，符合公式（23）（24）（26）成立的条件。（39）假设的弓步数据中加入了手的参数，将其分别代入（23）（24）（26）三个公式，计算出弓步时肢体相对动量对攻击力的影响（表三、图15）。

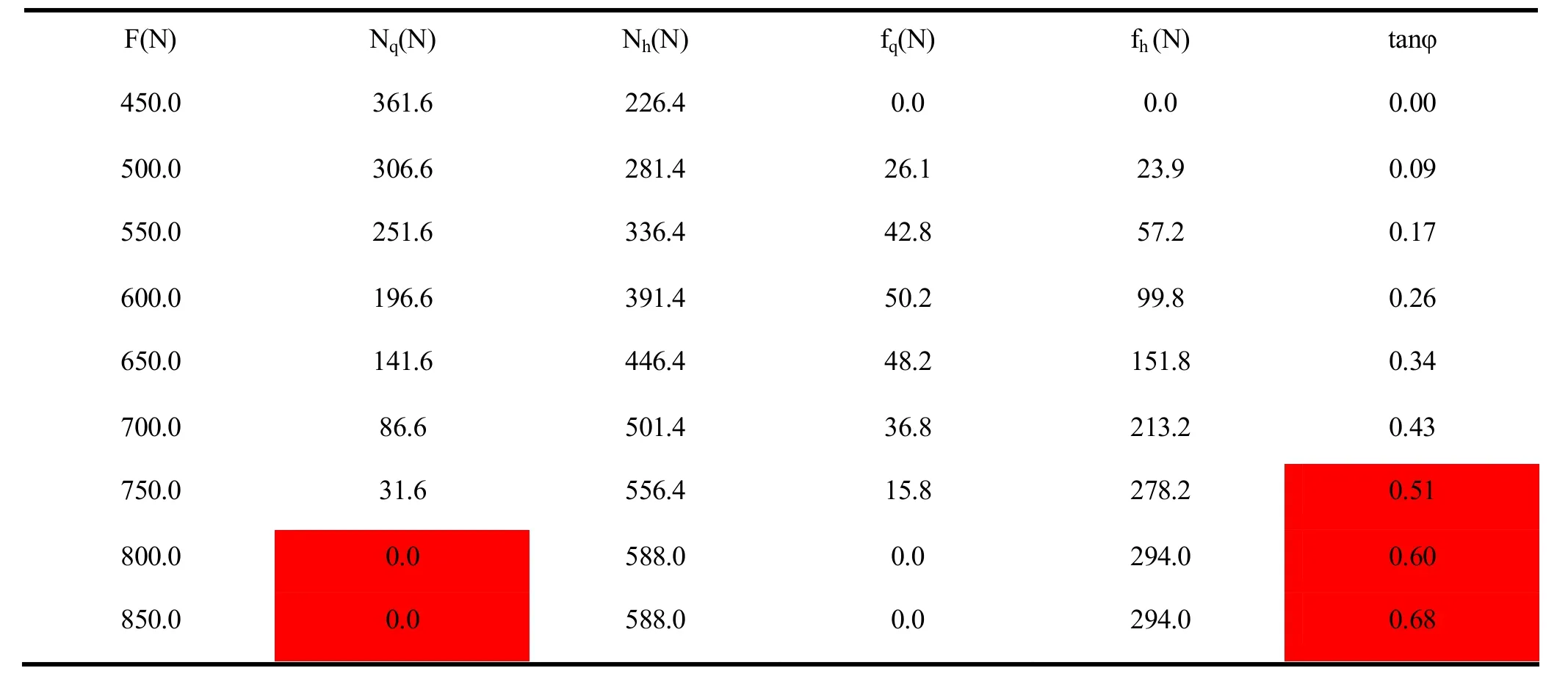
表3 弓步时肢体相对动量对攻击力的影响

表3分析：由第1栏和第2栏可见前脚正压力随水平外力增加而减小，采用（26）式计算，当水平外力是778.7时正压力变成零，这是失根的临界点。由第1栏和第6栏可见力线角随水平外力增加而增加。采用（24）式计算，当水平外力是744时力线角等于摩擦角，这是打滑的临界点。由上述可知，带有爆发力的弓步在肢体相对动量作用下，相比较只有传递力的弓步，虽然提高了450牛顿的攻击力，也缩小了打滑与失根时水平外力的差，但仍然是打滑先于失根，所以该弓步将以打滑而失效。

图15是引入爆发冲击力后各力随水平外力的变化曲线。水平轴是水平外力， 单位是牛顿（N）。竖直轴是各力的数值，单位也是牛顿（N）。

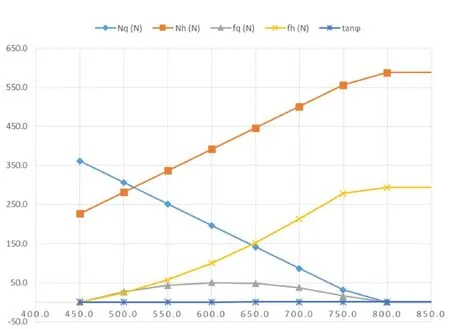
图15 引入爆发冲击力后各力随水平外力的变化曲线

图15分析：将图14与图15比较，图15的曲线完全向右拓展了200牛顿。这200牛顿就是爆发冲击力。也就是说，运用爆发发劲使弓步的总攻击力增加了200牛顿。爆发冲击力对正压力及摩擦力的关系没有影响.

当力线角增至摩擦角后，水平外力大于（26）式右端，摩擦力等于正压力和摩擦系数的乘积。（23）变为：

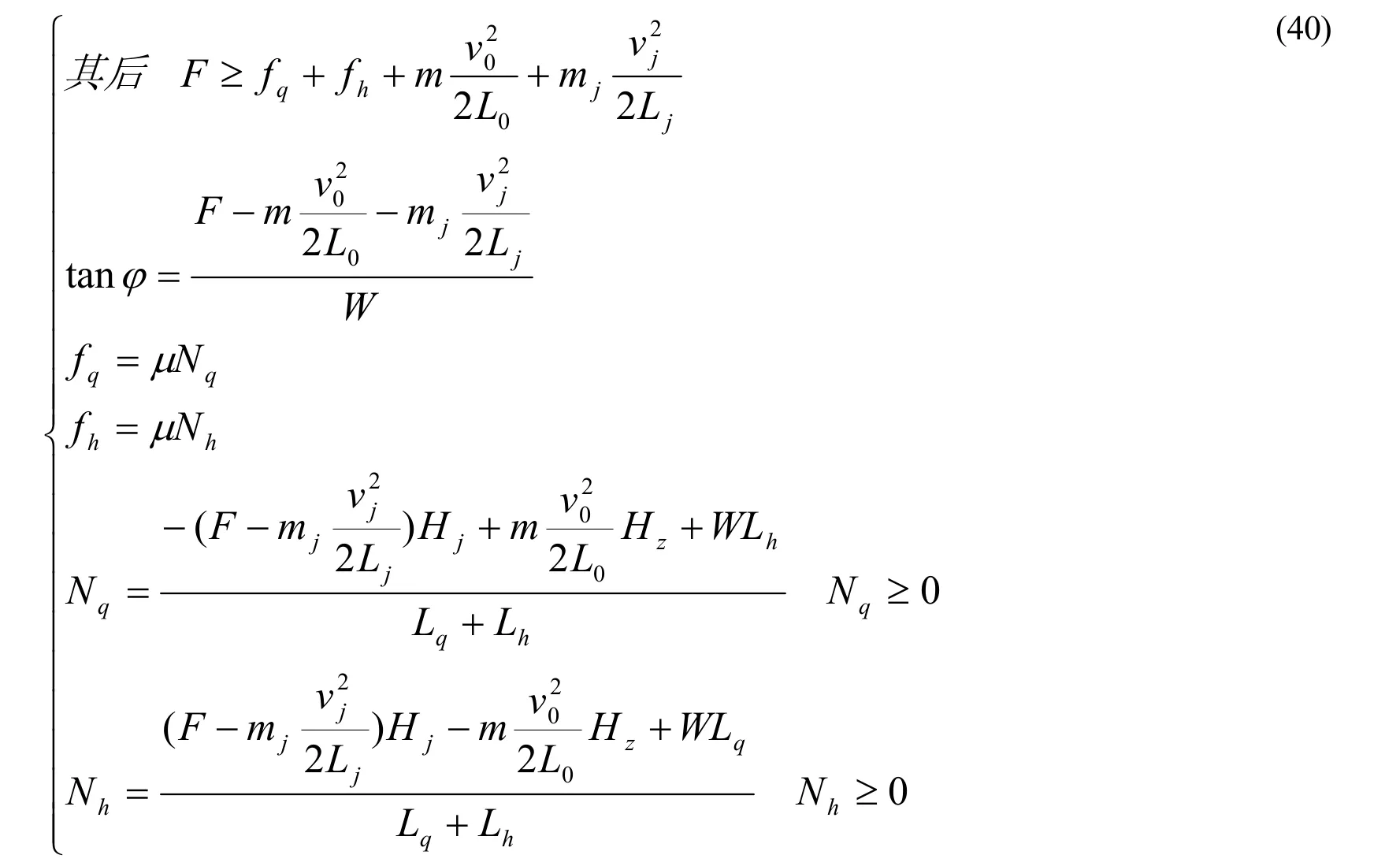
用（40）式计算表三中自F=750N 以下各行（至下一个临界条件）。可知，当水平力等于（24）式右端时，前脚正压力递减至零，后脚正压力递增至588牛顿。588牛顿正好是重力的全部。其后，当水平力大于（24）式右端时，（40）式就变为，

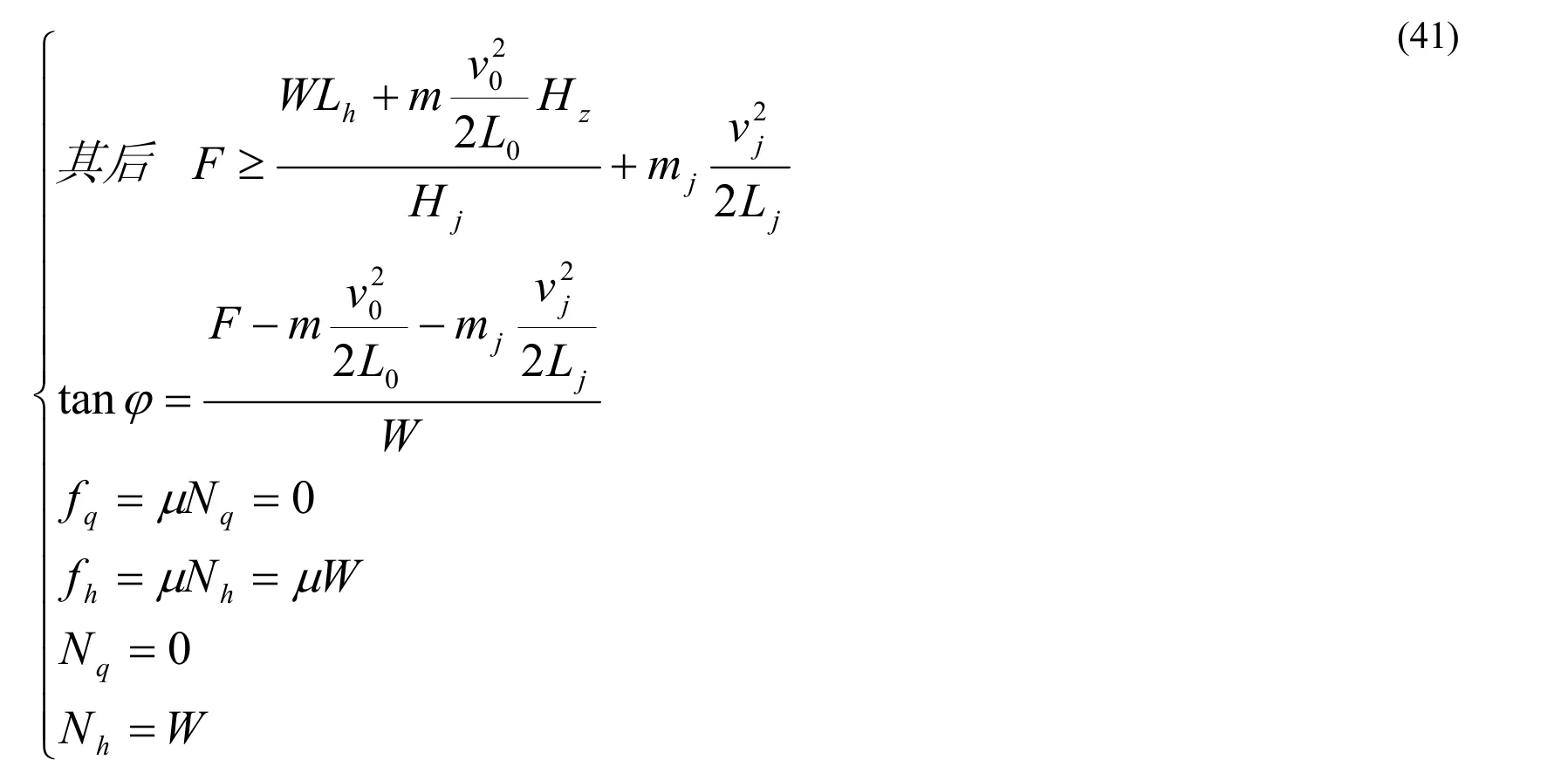
用（41）式计算表三中自F=800N 以下各行。可知，前脚摩擦力增至峰值后递减，当该脚正压力为零后摩擦力也为零。当前脚摩擦力为零后，后脚摩擦力增至294N并保持不变。294N就是全部由重力产生的摩擦力，等于重力和摩擦系数的乘积。

四、坐步的水平攻击力计算与分析

图16是坐步的人体刚体模型，与弓步的人体刚体模型相比，弓步的重心靠近前脚，坐步的重心靠近后脚。

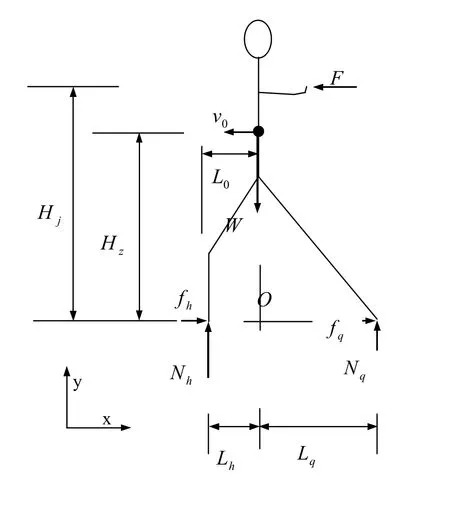
图16 坐步人体刚体模型

依照弓步的水平攻击力计算及分析的思路，也是先分析坐步的水平攻击力只有传递力的情况，仍采用公式（27）（28）（29）计算，将（42）中假设数据分别代入其中，计算出坐步时各力及力线角随水平外力的变化（表四、图17）、以及打滑的临界条件和失根的临界条件。

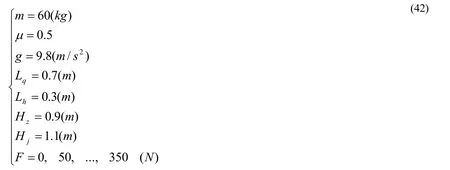
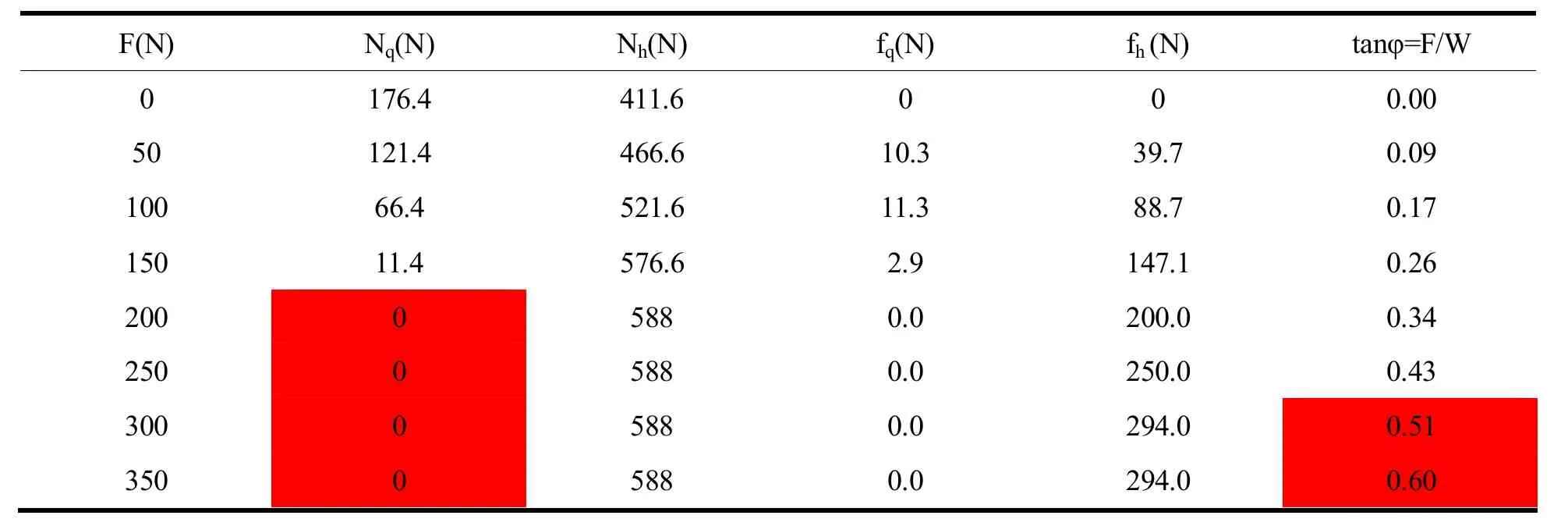
表4 坐步时各力及力线角随水平外力的变化

表4分析：坐步时失根先于打滑。

图17是各力随水平外力的变化曲线。水平轴是水平外力， 单位是牛顿（N）。竖直轴是各力的数值，单位也是牛顿（N）。

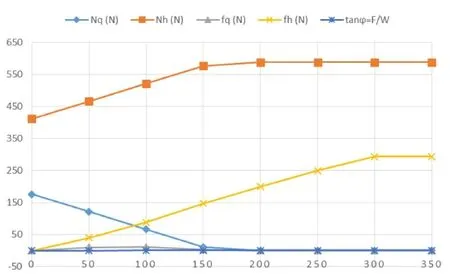
图17 各力随水平外力的变化曲线

图17分析：当水平力等于（29）式右端时，前脚正压力递减至零，后脚正压力递增至588牛顿。其后，水平力大于（29）式右端时，（27）式就变为：

用（43）式计算表四中自F=200N 以下各行（至下一个临界条件）。当力线角增至摩擦角后，摩擦力等于正压力和摩擦系数的乘积，（43）式就变为：

用（44）式计算表一中自F=300N以下各行。前脚摩擦力增至峰值后递减，当该脚正压力为零后摩擦力也为零。当前脚摩擦力为零后，后脚摩擦力增至294N并保持不变。294N就是全部由重力产生的摩擦力，等于重力和摩擦系数的乘积。

坐步和弓步相比有两点不同：一是弓步临界于打滑，坐步临界于失根；二是坐步的临界力远小于弓步的临界力。所以，向前攻击的功能，弓步强于坐步。

五、“发劲如放箭”和“引进落空”技术的分析

“发劲如放箭”和“引进落空”是太极拳的技术要求。“发劲”即是向前攻击的力，归于发放；“引进”即是向后拉的力，归于收引。

力是矢量，向前攻击的力表示为正值，向后拉的力表示为负值。前文代入正值计算了向前攻击的能力，现在代入负值计算向后拉的能力。

为计算坐步的拉力，将（42）所设数据中最下一行改设为：

将数据（45）和（42）中前七项分别代入公式（27）（28）（29），可得出各力随水平外力的变化表格和曲线（此处从略），以及失根的临界值F=-374.2N 和打滑的临界值F=-294N。由计算数值可见：打滑先于失根。

为计算弓步的拉力，将（30）所设数据中最下一行改设为：

将数据（46）和（30）中前七项分别代入公式（27）（28）（29），可得出各力随水平外力的变化表格和曲线（此处从略），以及失根的临界值F=-160.4N 和打滑的临界值F=-294N 。

由计算数值可见：失根先于打滑。

表5列出弓步和坐步的临界性质，表中第2、3栏列出了弓步和坐步的发放性质；第4、5栏列出了弓步和坐步的收引性质；第2行是先发生临界条件的类别；第3行是临界数值。

表5 弓步和坐步的临界性质

表5分析：

第2栏显示，弓步推发出294牛顿力，然后两脚打滑，从此不可能提供更大的推力。第3栏显示，坐步推发出160.4牛顿的力，然后前脚失根，从此不可能提供更大的推力。第2、3栏比较，弓步比坐步更适合用于发劲。

第4栏显示，坐步收拉出294牛顿力。然后两脚打滑，从此不可能提供更大的拉力。第5栏显示，弓步收拉出160.4牛顿力，然后后脚失根，从此不可能提供更大的拉力。第 4、5栏比较，坐步比弓步更适合用于收劲。

人是由肌肉和骨骼组成的柔体，发力时无论是向外推还是向内拉，都是通过变换体型来实现的。人体的刚体模型只是提供了某个瞬时的体型力学分析。发劲宜由坐步始而弓步终，坐步提供前弓的准备，弓步提供发劲的力学优势。类似的，收劲宜由弓步始而坐步终，弓步提供后坐的准备，坐步提供收劲的力学优势。采用弓步向前发劲可直攻对方重心，杨式太极拳的主要着式“揽雀尾”中的“挤”是典型的前攻型技术。

采用坐步向后收引或拉动时需要因时而宜灵活运用。如果是有意识化解对方攻势或以退为进诱使对方失重，都可保持我方不失根；如果对方攻势很强，或者我方要顺势发放，最好引入横向作用力，以使对方的攻击力偏离我方重心。杨式太极拳 “揽雀尾”一式中“按”的前半部就是典型的向后下牵引的引进落空技术，“捋”就是典型的向横向、向后下拉拽的引进落空技术。

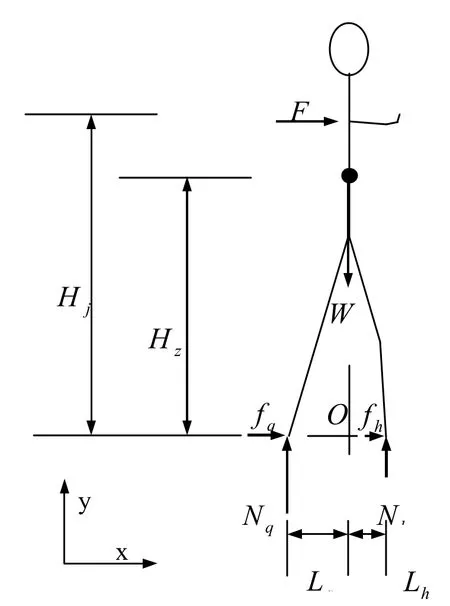
图18 宽弓步侧向刚体模型

六、“牵动四两拨千斤”的分析

太极拳讲求“牵动四两拨千斤”，这是以巧取胜、以小力胜大力的策略和技术，其中涉及人体侧向和纵向的稳定性。

（一）“牵动四两拨千斤”的横向效应

图 18是宽弓步侧向刚体模型，借此分析宽弓步侧向的抵抗力，也即“牵动四两拨千斤”的横向效应。宽弓步侧向两脚之间的距离一般是一肩宽，大约35厘米，通常一脚外撇45度，大约增加了5厘米两脚间的距离，增强了侧向稳定度。这样，两脚之间的平行距离，也即弓步的宽度为 40厘米。按三七分，前脚（直脚）到重心横向距离约12厘米，后脚（弓脚）到重心横向距离约28厘米。

计算及分析：将（47）中假设数据代入其中公式（27），计算出弓步侧向各力及力线角随水平外力的变化（表6）。

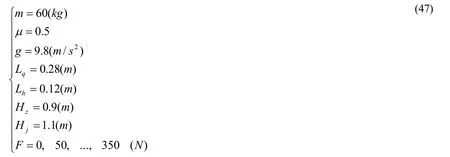
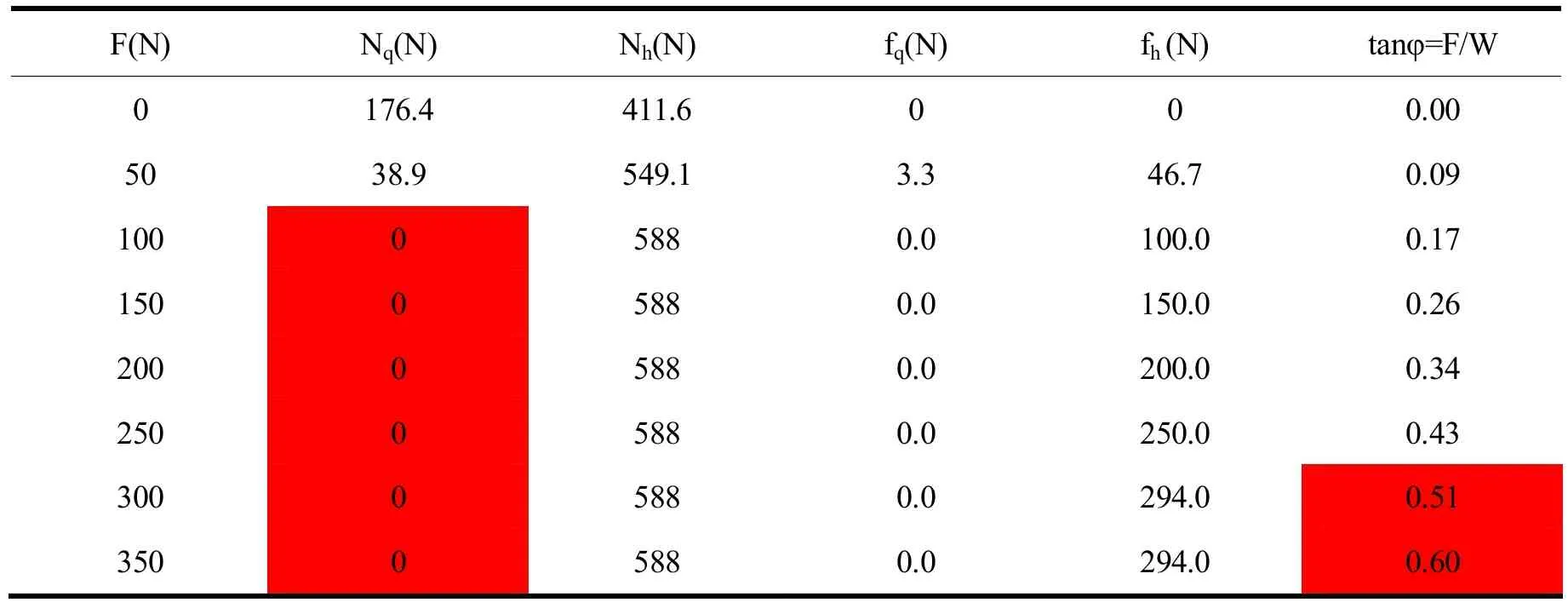
表6 宽弓步侧向各力及力线角随水平外力的变化

由表 6可见失根先于打滑，所只需计算失根值。将（47）式代入公式（29），计算出宽弓步前脚侧向失根临界值为，

弓步正向的打滑临界值为294牛顿。这表明宽弓步的侧向抗力功能比正向功能要差很多。注意这里是直脚失根，因为外力由直脚指向弓脚而把直脚上拔。这就证实了太极拳散打中套住对方的弓脚，从其身体上部向侧向攻击的做法是符合力学原理和巧妙省力、切实可行的。

从以上分析可以推论窄弓步和虚步的侧向抗力功能更差，更难以抵挡“牵动四两拨千斤”的侧向攻击。太极拳的“牵动四两拨千斤”战略战术多是从对方侧向或身体中心线一侧采用“拨动”的方法，攻击对方力学意义上的薄弱环节，即快捷又省力。

2、“牵动四两拨千斤”的纵向效应

参照图16坐步刚体模型，将（48）中所设相关数据代入公式（33），计算出坐步在质心速度向后时的抵抗力，也即表七坐步速度向后时各力及力线角随水平力的变化，

表7 坐步速度向后时各力及力线角随水平外力的变化

由表7可见失根先于打滑，所以只需计算失根值。将（48）代入公式（35）计算出前脚失根的临界力为，

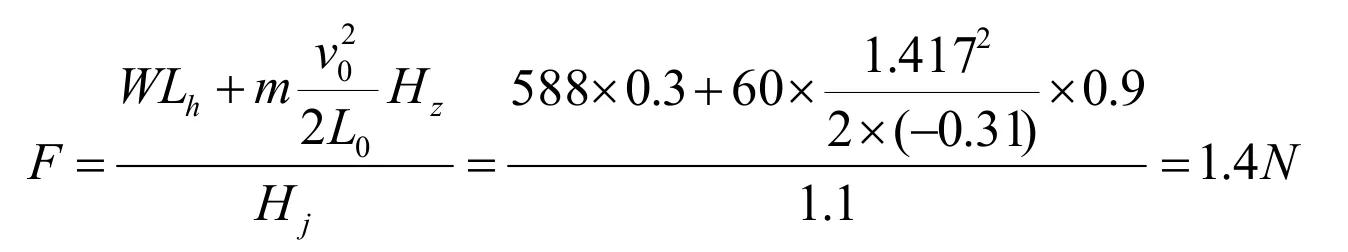
1.4N相当于我国旧时计量单位的四两多。

在数据（48）中，减速需要的距离是31厘米，后脚到重心的距离是30厘米。这就是说用1.4牛顿的力通过匀减速运动就能把对方推到其后脚外1厘米处，也就是说四两外力就可以把对方的重心推出支撑面。图16人体的质量是60公斤、质心水平初速度为1.417m/s，二者相乘的数值使其产生的较大动量。由于惯性（牛顿第一）定律，人体要保持这个速度。要在静止时分析人体的平衡状态，先要把这个动量减到零。根据牛顿第二定律，减速需要力。在本例中千斤力就是这个减速人体需要的力。这个力不是外力，而是自身克服惯性需要的力。四两拨千斤的意思就是四两外力推波逐澜于千斤惯性力。

惯性力产生于自身的动量，不是产生于两个物体间，只与人体的质量和速度相关。人的自身力量可称为劲，《太极拳发劲的动量传递解析》一文把劲定义为动量，动量可以传递。因此，上述例子可以看作是我方将小部分劲（四两力）适时传递给对方，与对方的劲（千斤惯性力）叠加，使对方失根。这里包括了劲的产生和运用两个方面，是一种太极功夫，需要锻炼而成。

尤其是劲的运用至关重要，运用的好，可以使自己平衡对方失稳；运用不妥，容易被对方借用导致自己失稳。即使自己单练也要注意，稍有不慎就会使自己失稳。

劲的恰当运用还与对方的状态密切相关。如果对方能灵活变换自己的速度方向，那我方的四量力可用来防止对方的逆向运动。如果对方向后的速度较大，我方可以乘势而进，顺势发力，完全可以把对方推出一丈（3米）之外。

试算一例，假设具有爆发力的弓步在发出750牛顿力时将对方向后推了0.3米，并迫使对方重心移到身后（后脚之外）以跳跃式后退，而自身保持稳定。750牛顿的力将对方向后退是所做的功是750（力）×0.3（距离）=225焦耳，这足以使对方后退4米多（一丈以上）。这是基于功的原理，是假设对方每退一步是50厘米，并打滑10厘米。这样，对方每打滑一次耗能588（重力）×0.5（摩擦系数）×0.1（距离）=29.4焦耳，完全消耗掉225焦耳就要跳出8.6步（225÷29.4），也就是说对方被打出了0.5×8.6=4.3米。可见，历史上太极拳名家一掌将人打出一丈之外，或将人腾空发出挂到墙上的故事是有力学依据的，是确实可信的。

七、小结

本研究表明，运用力学的方法、数学的方法研究太极拳能够有效揭示太极拳的奥妙，采用人体刚体模型依据力学原理对太极拳作隔离体分析是运用现代科技理论研究太极拳的有效途径。太极拳的技术动作、技术原理、训练要求等都蕴含着深厚的力学原理，有许多方面可以运用数学公式进行定量分析、精确分析，使其更显科学水平。

本研究采用平面刚体模型、从水平作用力入手分析是一个率先，也仅是一个开头，还受到某些局限，还需要进一步开拓思路、创新方法，从更广泛的力学角度进行深入研究。三维人体运动模型是近代的研究热点［8］，也是本文深入研究的需要。采用三维人体刚体模型模拟太极拳各种发力，通过隔离体分析更加深入解释太极拳力学原理，更加全面揭示太极拳奥妙将是下一步的研究方向。

［1］武禹襄. 太极拳论［M］. 手抄本.

［2］杨澄甫. 太极拳说十要［M］. 手抄本.

［3］马承九. 太极拳的科学观［M］. 台北：东大图书公司，1994.

［4］肖飞. 太极拳的力学原理［M］. 北京：人民体育出版社，2009.

［5］GU Jie. Explosive and Sequential Strength in Tai Chi［J］. T’ai Chi， 2013， 37（3）.

［6］顾杰，郭振兴. 太极拳发劲的动量传递解析［J］. 邯郸学院学报，2013（4）.

［7］王宗岳. 十三势行功心解［M］. 手抄本.

［8］李振波，李华. 基于运动生物力学的三维人体运动模型［J］. 系统仿真学报，2006，18（10）.

（责任编辑：苏红霞 校对：李俊丹）

Analyze Taijiquan by Rigid Human Plane Model under Horizontal Force

GU Jie，GUO Zhen-xing，LV Meng
（Taiji cultural school， Handan College， Handan 056005， China）

For the first time this article proposes a human rigid body model to do a mechanical analysis for Taijiquan. The model comprises the common mechanical conditions， including the frame， mass， speed， attacking force， gravity，normal horizontal force， friction forces， etc. The model is analyzed by dynamic laws for taijiquan， which results in a few important conclusions. The gravity center should be inside the supporting area to maintain the balance. Skidding and root loss are two critical points. The body is in balance within the critical points. Beyond one of the critical point，the body will eventually loose balance. The horizontal attacking force comes from the friction force， the body overall momentum， and the momentum of the relative motion between limbs. Interior strength has two aspects: creating momentum and transfer force. The interior strength creates body momentum and transfer force. The balancing critical points are calculated for taiji solo and push hand. Numerical examples demonstrate the classical techniques of “throw like an arrow”， “bring in to empty”， “four ounces deflect thousand pound”

Taijiquan； mechanical analysis； rigid Human plane model

G852.11

A

1673-2030（2015）02-0082-26

2015-02-15

顾杰（1955—），男，江苏苏州人，邯郸学院太极文化学院客座教授，美国通用汽车公司高级工程师，美国奥克兰大学机械制造博士；郭振兴（1950—），男，河北邯郸人，邯郸学院太极文化学院原院长，高级政工师，华中科技大学铸造机械专业。