SPH并行计算方案及其在自由表面流动模拟中的应用*

周 浩，徐志宏，邹 顺，汤文辉

(1.国防科技大学 理学院， 湖南 长沙 410073； 2.国防科技大学 计算机学院， 湖南 长沙 410073)

SPH并行计算方案及其在自由表面流动模拟中的应用*

周 浩1，徐志宏1，邹 顺2，汤文辉1

(1.国防科技大学 理学院， 湖南 长沙 410073； 2.国防科技大学 计算机学院， 湖南 长沙 410073)

针对光滑粒子动力学主要计算量是近邻粒子搜索这一特点，提出了一种基于粒子分解的光滑粒子动力学并行计算方案。利用该方案可以方便地将任意串行光滑粒子动力学代码并行计算，而且每一个时间步内的信息传递量只和粒子总数有关，而和粒子的分布无关，因而特别适合于自由表面流动等大变形问题的并行数值模拟。对一个粒子总数为40万的三维溃坝问题的模拟结果表明：此方案能达到的最大加速比约为16，这一结果可能比空间分解方案(不考虑动态负载均衡)更优。

光滑粒子动力学；并行方案；粒子分解；空间分解

(1.CollegeofScience,NationalUniversityofDefenseTechnology,Changsha410073,China；

2.CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073,China)

多数数值方法在处理大变形时存在一定困难。光滑粒子动力学(SmoothedParticleHydrodynamics,SPH)[1-2]方法作为一种无网格的拉格朗日方法，在处理自由表面流动等大变形问题时具有很大的优势，近年来其应用已经扩展到很多领域。又因为它的拉格朗日特性，界面附近物质的运动即代表了界面的运动，因此处理多相流也比较自然，且不需要额外的界面追踪算法。但是，SPH方法比有限差分、有限元等网格方法的计算量要大，因此在模拟规模较大的问题时经常需要并行计算。

SPH的计算过程和分子动力学(MolecularDynamics,MD)类似，所以其并行也和MD类似。Plimpton[3]总结了3种不同的MD并行方案，即空间分解，粒子分解和力分解。目前，文献中绝大多数SPH方法并行采用的都是空间分解方案，因为其信息传递量小，其缺点是编程实现复杂。

空间分解方案又可以分为静态和动态两种。静态空间分解时，每个处理器分配的空间始终固定。当所有粒子始终在计算域近似均匀分布时，这种方法能够得到极高的加速比。但是，在自由表面流动等实际问题中，粒子往往在空间中分布非常不均匀，这会使得负载严重不平衡，导致加速比较小。动态空间分解时，需要根据负载平衡原则每隔一段时间动态调整各个处理器空间的大小和位置，来保证所有处理器的计算量大致相等。调整处理器空间需要额外的计算时间，因此动态调整的频率要适当，而且调整算法也必须高效。

动态空间分解虽然能够高效地模拟大变形问题，但是实现起来非常复杂。如Ferrari等[4]在采用并行SPH方法模拟三维溃坝问题时，采用第三方软件包METIS来动态调整处理器空间。在METIS中，首先需要在空间布满背景网格，再根据每个小网格中粒子数的多少来给每个小网格一个权重，来实现每个处理器空间大小不等但是计算量近似相等，用以实现负载平衡。Marrone等[5]采用并行SPH方法模拟行船产生的波浪及其破碎时，只在主要流动方向上动态调整，因为这能极大地简化编程，并且指出存在主要流动方向的特征越明显，并行模拟的加速比越高。并行SPH程序JOSEPHINE[6]和开源软件parallelSPHYSICSv2.0在模拟二维自由表面流动时，也都只在一个主要流动方向上实现了动态调整，因此，当流动有多个主要方向时，加速比会下降。总的来说，动态空间分解的实现复杂度严重限制了其在SPH并行模拟中的广泛使用。

Plimpton描述了MD的粒子分解并行方案，其基本思想是每个处理器负责维护固定的某一部分粒子。这种方案的最大优点在于并行很容易在串行代码的基础上实现[3]。但是，由于MD中的分子由若干原子组成，分子具有一定内部结构，需要考虑其旋转等因素，而且与每个分子有相互作用的分子列表可以若干时间步更新一次，所以其主要计算量在于分子间相互作用力的计算。而SPH中粒子间的相互作用力相对简单，而且一般每个时间步都需要更新每个粒子的近邻粒子，因此其主要计算量在于近邻粒子搜索[7]。

针对SPH方法的上述特点，提出了一种简单的粒子并行方案。这种方案能够达到可观加速比，有效节约计算时间，而且方案实现非常简单，负载均衡，每个时间步的信息传递量与粒子分布无关，可以十分方便地采取任意奇数个处理器并行计算。但是，这种方案的信息传递量较大，不适合上百个处理器的大规模并行计算。

以二维圆柱绕流和三维溃坝问题为例，比较了这种粒子并行方案和空间分解方案(不考虑动态负载均衡)的计算时间或加速比。在这两个算例中，前者粒子分布始终非常均匀，而后者则是典型的大变形问题，粒子分布严重不均匀。这两个算例的对比可以明显地展示出粒子并行方案只适合于粒子分布严重不均匀问题的并行模拟。SPH静态空间分解方案在开源软件平台OpenFOAM的基础上实现，粒子分解方案采用Fortran90语言加上讯息传递接口(MessagePassingInterface，MPI)消息传递库实现。本文所有模拟都是在广州超算中心的天河二号计算机上完成。

1 控制方程及其SPH离散

假设系统中没有温度梯度，黏性流动的控制方程为如下N-S方程

(1)

(2)

其中:ρ，u,p,t分别为密度、速度、压力和时间；υ2u为黏性力；υ为运动黏性系数；fe为外力。控制方程式(1)和式(2)右边各导数项的SPH离散形式如下：

(-ρ

(3)

(4)

(5)

其中，式(5)为Morris基于有限差分和SPH离散提出的黏性力计算模型[8]。本文模拟中时间积分采用蛙跳法。

对不可压缩流体采用弱可压来近似，通过将流体的密度变化控制在1%以内来近似实现不可压[9]。本文中采用如下最常用的物态方程其中，γ=7，c0取粒子最大速度的10倍。

(6)

2 SPH并行方案

现阶段文献中SPH并行绝大多数采用的是空间分解方案。本文实现并比较了空间分解和粒子分解这两种并行方案各自的优缺点。

2.1 空间分解方案

空间分解方案是目前使用最普遍的方案，其基本思想就是首先将整个计算域划分为若干不重叠的子域，然后每个处理器负责一个子域，如图1所示。

图1 空间分解示意图Fig.1 Domain decomposition

当计算满足局域性(任何一点在下一时刻的值只和包括这点的某局部空间相关)时，只有在子域之间的交界处才需要传递信息，如图1中的实心粒子部分。因此，划分子域的一个原则就是让交界面积尽量小，这代表了信息传递少，即并行带来的额外时间开销小。另一个原则是尽量保持每个子域的计算量相等，即负载均衡，这样才能达到较高加速比。

在欧拉类网格方法中，往往是网格的数量代表了计算量。由于网格是不动的，所以负载均衡比较容易实现。但是SPH方法属于拉格朗日方法，粒子数量大致代表了计算量，大变形条件下，粒子占据的空间可能发生很大变化，如模拟溃坝、气体扩散、超高速碰撞等问题。这会导致每个子域的粒子数量严重不平衡，导致并行效率低下。一种做法是采取动态负载均衡，即模拟过程中如果发现负载不均衡，就按照一定策略将空间重新分解，如开源软件parallelSPHYSICSv2.0的使用手册中给出的二维溃坝问题的模拟结果，其动态负载均衡如图2所示。

图2 动态负载均衡Fig. 2 Dynamic load balancing

图2中有3个垂直方向的处理器边界，它们将整个计算域划分为4个子域，每个子域用一个处理器计算。当粒子整体向右移动时，每个处理器边界也适当向右移动，来尽量保证每个子域的粒子数相等。

动态空间分解虽然能够解决负载不均衡问题，但是实现起来复杂，所以本文不考虑动态空间分解。

2.2 粒子分解方案

本文针对SPH方法的主要计算量在于近邻粒子搜索这一特点，提出并实现了一种新的粒子分解方案，其基本思想是将找出所有近邻粒子对这样一个大任务划分为np(处理器数)个小任务，每个处理器完成一个。

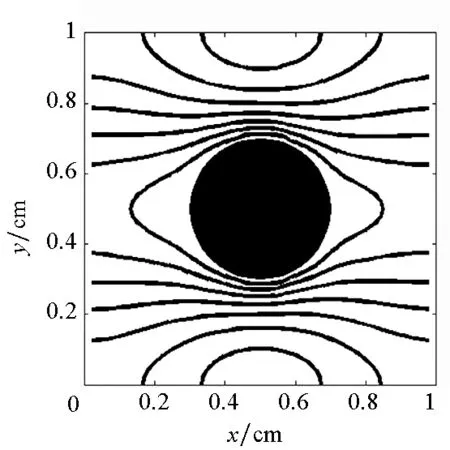
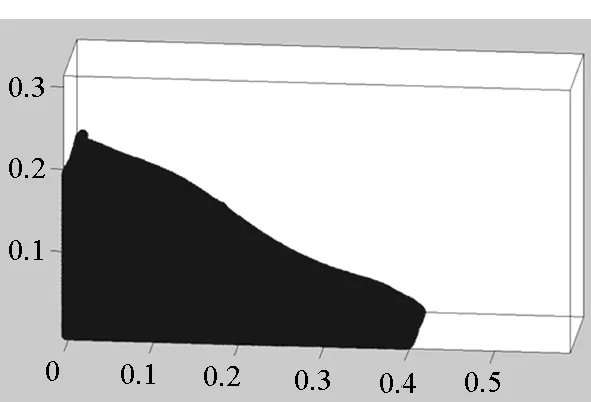
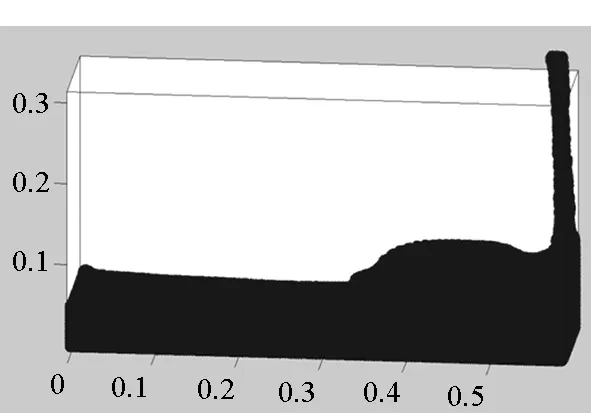
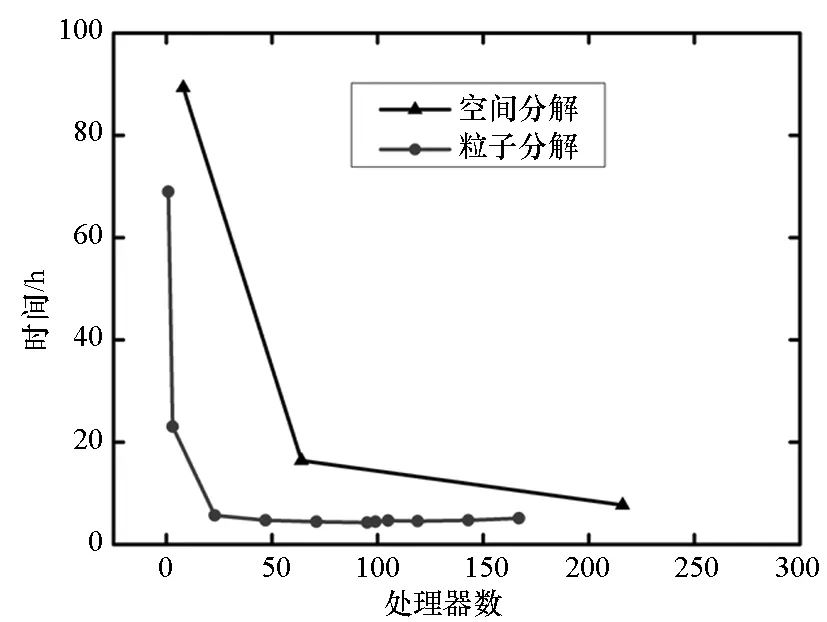
首先将所有粒子依据编号从小到大分为np个组Gm(m=1,2,…,np)，每个组的粒子数近似相等，约为N/np(其中N为粒子总数)，处理器m维护组Gm。当粒子i和粒子j是近邻粒子时，可以用(i,j)来表示这一近邻粒子对，为了避免重复，因此要求i

由于m≤n，可知子集(Gm,Gn)有np(np+1)/2个，且相互不重叠。每个处理器负责(np+1)/2个。显然，当np为奇数时，(np+1)/2为整数，此时，每个处理器的负载非常均衡。下面以np=5为例来说明这些子集在处理器上的分配策略，如表1所示。

表1 近邻粒子对在不同处理器之间分配策略

由表1可以看到，处理器P1负责维护G1这组粒子。在每个时间步长内，P1首先需要将G1组粒子的所有信息发送给P4和P5，因为P4需要找出近邻粒子对子集(G1,G4)，P5需要找出(G1,G5)；然后P1搜索被分配的近邻粒子对(本文采用树搜索算法)并同时计算相互作用力；最后P4和P5将所计算的G1组粒子受到的部分作用力发送回P1，由P1更新G1这组粒子的状态。

处理器P2的计算过程类似，即P2首先将G2组粒子的所有信息发送给P1和P5；然后寻找被分配的近邻粒子对并同时计算相互作用力；最后P1和P5将所计算的G2组粒子受到的部分作用力发送回P2，由P2更新G2这组粒子的状态。其他处理器的计算过程也类似。

于是，每个时间步可以分为如下4步：粒子信息发送、近邻粒子搜索并同时计算粒子间相互作用力、相互作用力信息交换和更新粒子状态。分别统计每步的计算时间，可以得到：第1步和第3步为信息传递，时间随着处理器的增加而缓慢增加；第2步是主要计算量，随着处理器的增加而单调减小；第4步也是计算，时间几乎可以忽略不计[10]。

可以看到，本粒子分解方案有如下特点：①一个时间步长内的所有通信为每个处理器调用一次广播函数和一次求和归约函数，实现非常简单；②每个处理器的计算量和通信量都大致相等，负载非常均衡；③每步的信息传递量为O(N)，与粒子的分布无关；④可以十分方便地采取任意奇数个处理器并行计算。

3 两种并行方案的比较

3.1 二维圆柱绕流

模型参数与文献[8]中的圆柱绕流算例一致，雷诺数为0.03。初始时，X方向和Y方向各均匀分布1000个粒子，总粒子数为100万。X方向为周期性边界条件，对应的实际物理问题为无限长管道中均匀分布无数个圆柱。图3给出了SPH模拟结果和有限元模拟结果的对比，其中图3(a)为文献[8]中的有限元模拟结果，图3(b)为本文模拟结果。

(a)有限单元法(a)Finte Elmemt Modeling

(b) 光滑粒子动力学(b)Smoothed particle hydrodynamics图3 SPH和有限元模拟的速度大小等值线对比Fig.3 Contour lines of velocity magnitude using FEM and SPH for Re=0.03

分别采取两种并行方案，测得的加速比如图4所示。

图4 空间分解和粒子分解加速比随处理器的变化Fig. 4 Speed-up ratio of domain decomposition and particle decomposition with the change of processors

从图4可以看到，空间分解时，当处理器数目在小于100时，加速比反常地略高于理想值，其原因可能和缓存等硬件有关，文献[4-5]以及开源软件parallelSPHYSICSv2.0使用手册中都报告了类似的情况。当处理器数目为320时，加速比约为234.69，并行效率为73.34%。如果继续增加处理器数至640，加速比迅速降低为100.13，对应的并行效率为15.65%，因此结果没有在图4中给出。

粒子分解时，最多采用了93个处理器，此时的加速比为23.33，并行效率为25.09%。如果继续增加处理器数量，加速比则缓慢下降。

因此，对于粒子分布均匀的情况，空间分解的加速比远大于粒子分解。而且可以发现，粒子分解不适合上百个处理器的大规模并行计算。

3.2 三维溃坝问题

模型参数与文献[11]中的溃坝算例一致，初始水柱高0.292m，宽0.146m，容器宽度为0.584m。初始粒子总数大约为40万，时间步长固定为20μs，共计算了50 000个时间步长。图5为文献[11]给出的二维流体体积法(VolumeOfFluid，VOF)模拟结果，从左到右的时刻依次为0.2s，0.4s，0.6s和0.8s。

图5 溃坝问题的二维模拟结果[10]Fig. 5 2D VOF simulation of dam break

本文采用静态空间分解和粒子分解两种不同的并行方案对同样的问题进行了三维数值模拟。模拟的粒子分布如图6所示。

(a) t=0.2s

(b) t=0.4s

(c) t=0.6s

(d) t=0.8s图6 三维溃坝问题的SPH模拟Fig. 6 3D SPH simulation of dam break

可以看到，三维模拟结果和文献[11]中的实验及VOF模拟结果基本一致。为了和二维模拟结果对比，图7给出了0.8s时刻粒子分布的一个二维视图。

图7 0.8s时刻的二维视图Fig.7 2D view point at t=0.8s

从图7可以看到，流体在0.8s时刻形成了一个空腔，这和VOF计算结果吻合。

因为容器在X，Y，Z方向上的尺寸约为1∶4∶2，因此在空间分解时，X，Y，Z方向上的处理器个数取为n，4n，2n，从而让每个处理器分配的空间大小近似相等，总处理器个数为8n3。但是由于粒子在整个容器中的分布极不均匀，每个处理器上分配的粒子数实际上极不均匀，甚至多数处理器上没有粒子。本算例中，空间分解时处理器个数分别取为8，64，216，分别对应于n=1，2，3。

两种并行方案测得的计算时间如图8所示。

图8 空间分解和粒子分解计算时间随处理器的变化Fig.8 Total computing time of domain decomposition and particle decomposition with the change of processors

可以看到，空间分解的计算时间比粒子分解要长，而且计算时间随处理器数的增加缓慢下降。当处理器数为216时，空间分解需要约7.7h，加速比为9.0。此处加速比定义为speedup=T1/Tn，其中Tn为采用n个处理器并行计算的时间，T1为串行计算时间。由于空间分解程序的计算时间较长，没有测试其串行计算时间，所以其串行计算时间采用粒子分解程序的串行时间。计算中还发现，当处理器数为216时，绝大多数处理器中没有粒子，这是由溃坝问题中粒子分布不均匀的特点以及没有动态负载均衡造成的。

粒子分解时，当处理器数为23时，计算时间为5.7h，几乎已经降到最低值，且计算时间比空间分解方案的最优值少。当处理器数为95时，需要的时间最少，为4.3h，最大加速比为16.1。如果继续增加处理器数，计算时间缓慢增加。

4 结论

本文提出了一种非常简单的基于粒子分解的SPH并行方案，并以二维圆柱绕流和三维溃坝问题的SPH并行模拟为例，比较了粒子分解和空间分解的计算时间或加速比，得到了以下主要结论：

1)当粒子分布均匀时，SPH并行应该采用空间分解方案。此时，只有处理器边界处有信息传递，信息传递量小，能够达到非常大的加速比。而粒子分解的加速比相对较小。

2)当粒子分布非常不均匀时，SPH并行可以采用粒子分解方案。此时，静态空间分解的负载严重不平衡，导致加速比较小。而粒子分解采用较少处理器就能达到可观加速比。

3)从文中两个算例可以看出，当问题规模在40万～100万左右时，粒子分解方案的加速比固定在16～23左右。在粒子分布非常不均匀的情况下，这一结果可能比静态空间分解更优。因而，本文提出的粒子分解方案在自由表面流动模拟中具有一定优势。

References)

[1]LucyLB.Anumericalapproachtothetestingofthefissionhypothesis[J].AstronomicalJournal, 1977, 82: 1013-1024.[2]MonaghanJJ,GingoldRA.ShocksimulationbytheparticlemethodSPH[J].JournalofComputationalPhysics, 1983, 52(2): 374-389.

[3]PlimtonS.Fastparallelalgorithmsforshort-rangemoleculardynamics[J].JournalofComputationalPhysics, 1995, 117(1): 1-19.

[4]FerrariA,DumbserM,ToroEF,etal.Anew3DparallelSPHschemeforfreesurfaceflows[J].Computers&Fluids, 2009, 38(6): 1203-1217.

[5]MarroneS,BouscasseB,ColagrossiA,etal.Studyofshipwavebreakingpatternsusing3DparallelSPHsimulations[J].Computers&Fluids, 2012, 69: 54-66.

[6]CherfilsJM,PinonG,RivoalenE.JOSEPHINE:aparallelSPHcodeforfree-surfaceflows[J].ComputerPhysicsCommunication, 2012, 183(7): 1468-1480.

[7]MoulinecC,IssaR,LatinoD,etal.High-performancecomputingandsmoothedparticlehydrodynamics[C]//ProceedingsofParallelComputationalFluidDynamics,Lyon, 2008.

[8]MorrisJP,FoxPJ,ZhuY.ModelinglowreynoldsnumberincompressibleflowsusingSPH[J].JournalofComputationalPhysics, 1997, 136(1): 214-226.

[9]MonahanJJ.SimulatingfreesurfaceflowswithSPH[J].JournalofComputationalPhysics, 1994, 110(2): 399-406.[10] 周浩，汤文辉，冉宪文，等. 光滑粒子流体动力学的一种并行数值计算方案[J]. 航天器环境工程， 2012， 29(1): 23-26.ZHOUHao,TANGWenhui,RANXianwen,etal.Spacecraftenvironmentengineering[J].SpacecraftEnvironmentEngineering, 2012, 29(1): 23-26.(inChinese)[11]DoringM,AndrillonA,AlessandriniB,etal.SPHfreesurfaceflowsimulation[C]//Proceedingsofthe18thInternationalWorkshoponWaterWavesandFloatingBodies,LeCroisic, 2003.

SPH parallel schemes and its application in free surface flow simulation

ZHOU Hao1, XU Zhihong1, ZOU Shun2, TANG Wenhui1

Forthemaincomputationofsmoothedparticlehydrodynamicswasfinitenearestparticlesearch,anovelschemetoparallelizethesmoothedparticlehydrodynamicsmethodbasedontheconceptofparticledecompositionwasproposed.Anyserialsmoothedparticlehydrodynamicscodecouldbeeasilyparallelizedbyusingtheproposedscheme.Theamountofinformation,whichwastransformedineachtimestep,dependedonlyonthetotalnumberofparticles,butnotonthespatialdistributionofparticles.Therefore,theproposedschemewasparticularlyusefulfortheparallelsimulationofcasesinvolvedviolentfreesurfacemovements.Fromthesimulationresultsofa3Ddambreakcasewithatotalnumberof0.4million,theproposedschemecanachieveaspeedupratioabout16,whichprovesthattheproposedschememaybeisbetterthanthedomaindecompositionscheme(withoutconsideringdynamicloadbalance).

smoothedparticlehydrodynamics;parallelscheme;particledecomposition;domaindecomposition

2014-07-08

国家自然科学基金资助项目(61221491，61303071)，广州科信局基金资助项目(134200026)

周浩(1986—)，男，湖南常德人，博士研究生， E-mail: zhouhao12029014@163.com；汤文辉(通信作者)，男，教授，博士， 博士生导师，E-mail：wenhuitang@163.com

10.11887/j.cn.201504012

http://journal.nudt.edu.cn

TB

A