基于FPGA的串行结构递归神经网络LS-SVM实现
宋 鲁
基于FPGA的串行结构递归神经网络LS-SVM实现
宋 鲁
使用FPGA实现递归神经网络的LS-SVM串行计算结构,能有效降低并行计算结构对嵌入式系统硬件资源的消耗。该结构具有串行计算、并行传输的特点。采用verilog HDL来实现该结构,可以在编译阶段设置处理数据的字长,具有较强的灵活性。利用Altera Cyclone III系列FPGA完成LS-SVM训练的仿真实验。结果表明,该硬件实现方法很好地完成LS-SVM的分类训练,与现有的LS-SVM matlab软件包相比,达到相似分类准确率的情况下,具有更快的训练速度。
支持向量机(SVM)作为机器学习的一个研究热点,被广泛应用到工程领域中。目前,SVM的研究较多局限于软件实现。然而,这种方法在执行过程中需要巨大的硬件资源 。因此,研究SVM硬件实现架构是必要的。这种专用电路结构可以提高硬件资源的利用效率,从而降低芯片的面积、功耗、成本,提高速度和可靠性。
最早适用于VLSI实现的SVM学习电路采用Chua递归网络来解决受约束的二次规划问题,但其要达到精确解,惩罚因子会接近无穷大,硬件不易实现。随后出现了一些处理SVM学习过程的双层或单层结构的神经网络。不足之处在于,当不存在界内支持向量,即当所有支持向量机都为界上支持向量时,无法得到偏移量。
在双层网络的基础上,文献提出较为简单的单层递归神经网络拓扑结构来实现SVM学习,并在理论上证明了其收敛性和分类性能,与双层网络相比,其硬件实现更加简单。然而,当训练数据集较大时,并行系统将耗费过多的硬件资源,并行计算结构将不能满足嵌入式系统的要求。鉴于此,本文提出一种串行计算结构,使用FPGA实现基于递归神经网络的LS-SVM。该结构具有串行计算、并行传输的特点,计算核心单元采用复用的方式,硬件资源得到较大程度的缩减。
基于递归神经网络的LS-SVM
最小二乘支持向量机(LS-SVM)
LS-SVM分类器由Suykens等提出,它通过线性系统来求解二次规划问题。LS-SVM在原空间中求解如下优化问题:
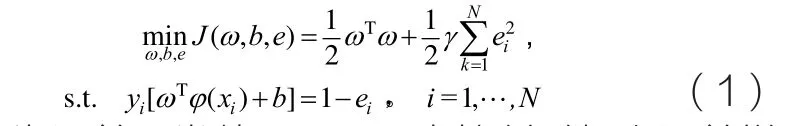
式中:e 为误差;常数γ>0,用来控制对超出误差样本惩罚的程度。问题(1)相应的拉格朗日函数为
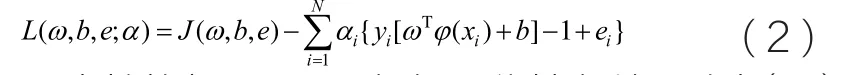
式中,αi为拉格朗日乘子。根据最优性条件,对式(2)求偏导并令其为0,得
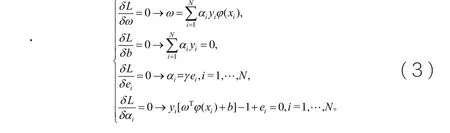
消除变量ω和e,可得到如下矩阵方程来代替二次规划问题:

其中,

设上述方程的解为α=[α1,...,αN],则LS-SVM分类器的决策函数为:
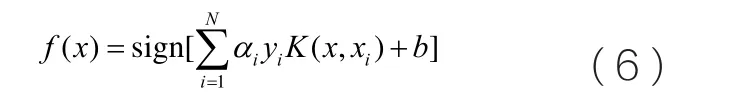
LS-SVM神经网络
在文献中,作者利用部分对偶原理,将SVM的二次规划问题转化为递归神经网络的动态方程求解问题。
对式(4)展开,可得

其中:qij=yiyjkij,kij(=k, xi) xj为核函数。若核函数满足Mercer条件,且对称阵QC=[qij]为半正定,则该问题只有一个全局最优解。
神经网络模型由下面的动态方程描述:

可以看出,该动态系统在平衡点处,即满足最优化条件(7)、(8)时,所提出的神经网络在平衡点处满足KKT条件。这样,当所提出的动态网络收敛到平衡点时,就可求解LS-SVM问题。式(9)、(10)两边同时积分可得:

式(11)、(12)可以用图1所示的递归神经网络来实现。
图1所示的神经网络是由(N+1)个神经元组成的递归网络;∑为累加器,传输函数f为一个积分环节。输入向量通过如下权矩阵W进入网络:

图1 实现LS-SVM的神经网络拓扑结构图

图2 神经元的verilog HDL运算流程框图

该网络结构很容易采用硬件电路实现。为在FPGA实现该结构,先将式(9)、(10)进行离散化处理,得
式中,∆T 为采样时间间隔,本研究取∆T=2-10s。式(14)、(15)可用逻辑门电路实现。
LS-SVM神经网络神经元FPGA实现
根据图1和式(14)、(15)可知,用FPGA实现LS-SVM分类功能的神经网络架构需要乘法累加器(MAC)、乘法器(MUL)、加法器(ADD)、减法器(SUB)和累加单元(AC)等运算单元。系统分别使用ROM单元和RAM单元,用于存储神经网络权值系数qij和每个神经元运算得到的αi值。神经元硬件实现以图1中第i个神经元为例,神经元的verilog HDL运算流程框图如图2所示。
在实现LS-SVM分类功能的神经网络时,神经网络权值系数qij在运算过程中保持不变,仅与训练数据集有关。在进行神经网络训练前,首先将权值系数qij计算好并存放在FPGA的ROM单元中。为了缩短开发时间,MAC、MUL、ADD和SUB等计算单元均采用开发软件QUARTUS II中的IP核实现。图2可以看出,每个神经元中ROM的读取、RAM的读取以及MUL(1)、MUL(2)的运算可以并行进行,从而可以节约每个神经元的运算时间。将网络训练的初始αi值存储在RAM中,当运算需要αi时,可直接从RAM中读取;下一个周期运算获得新的αi值存储在RAM中。RAM中的αi随系统运行一直处于更新状态,这就对系统中时序的控制提出了较为严格的要求。在进行神经网络训练时,只有在所有αi计算完成并存储在RAM中,下一个周期的训练才能进行,因为下一个周期的运算依赖于上一个周期的αi。以一个周期为例,说明LS-SVM神经网络神经元FPGA的实现,其流程图如图3所示。
图中,神经元按图3箭头所指的方向进行运算,依次从基本元件库中调用运算单元,从而完成式(14)中b 和式(15)中αi的计算。

图3 LS-SVM神经网络神经元实现流程图
LS-SVM神经网络串行计算的FPGA实现
LS-SVM串行计算的FPGA实现如图4所示。系统主要由系统时序控制单元(TCU)、Lssvm_alpha单元、Lssvm_bias单元、RAM读写单元、Judge单元、Add及Lock单元组成。各单元的功能简介如下。
(1)系统时序控制单元(TCU):负责整个系统的时序产生及控制,包括αi(i=1,…,N),b值运算时序的产生,RAM读写时序的产生,ROM读取时序的产生以及系统中加法器、锁存器等运算单元时序控制。
(2)Lssvm_alpha单元:在时序控制单元的控制下,串行逐个完成图2所示的每个神经元的计算。
(3)Lssvm_bias单元:当前周期所有的αi(i=1,…,N)值计算完成后,将αi(i=1,…,N)值存储在RAM中,通过时序控制模块将αi(i=1,…,N)值从RAM中读出,并与yi值进行乘法累加运算,以获得b。与此同时,该单元并行将运算获得的b值送入Lssvm_alpha单元,进行b值的更新,为下一个周期的运算做准备,该单元的模块结构图如图5所示。
(4)RAM读写单元:负责αi(i=1, 2,…,N)存取,为Lssvm_alpha单元、Lssvm_bias单元以及加法器单元提供本周期的αi(i=1,…,N)值,同时从Lock锁存器单元中获得下一周期计算得到的αi(i=1,…,N)值,并按顺序存储。
(5)Judge单元用于判断每个神经元的输出增量值是否小于设定阈值,若N个神经元的输出增量值均小于设定阈值,则判断αi(i=1,…,N)训练完毕。
(6)Add单元将上一个周期的αi值与本周期神经元输出的增量值相加,通过Lock单元将获得的αi逐个锁存起来,并将所有计算完成的αi(i=1,…,N)统一传给RAM单元存储。
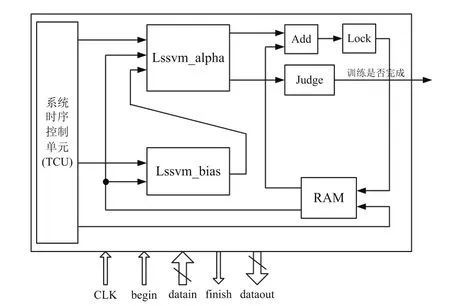
图4 LS-SVM串行计算实现框图
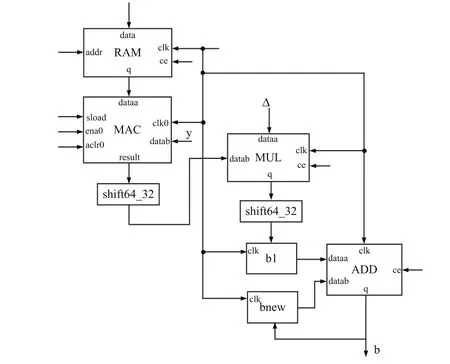
图5 Lssvm_bias单元的模块结构图

图6 实验1的FPGA实现运行结果
实验结果及分析
通过仿真实验测试串行LS- SVM结构的性能,并将其与LS-SVM Matlab软件包运算值进行比较。实验所用的计算机配置为:Intel (R)Core(TM)2Duo CPU2.40GHz,1GB内存;Matlab版本为R2009a。硬件平台为Altera公司的Cyclone III系列FPGA,系统仿真频率为100MHz。软件平台为Quartus II编译环境及Verilog HDL硬件编程语言。其中,采用verilog HDL实现该串行计算结构具有较强的灵活性,因为可以在编译阶段指定处理数据的字长。
(1)实验1。选取植物数据集(Iris data)中Irissetosa与Iris-versicolor共10个样本点作为训练数据,2类中剩余的90个样本作为测试数据。Iris-setosa与Iris-versicolor线性可分,4个属性分别为sepal length、sepal width、petal length和petal width。核函数选择高斯核函数,sig2=2.25;γ-1=0.2。图6为参数α的FPGA平台实现结果,“result”中的10个数分别代表参数α0,α1,…,α9,Judge模块输出信号all_ok为“1”时,α训练完成。将FPGA训练的α0, α1,…,α9、b值代入LS-SVM Matlab软件包对测试数据集进行预测,结果如表1所示:其中,分类准确率达到98.89%,与LS-SVM Matlab软件包获得的分类准确率相同。从参数α的收敛时间来看,FPGA的计算速度明显优于LSSVM Matlab软件包的运算速度。结果表明,串行结构的LS-SVM FPGA实现架构同样可以很好地解决实验1的分类问题。可见,本文方法对解决线性可分分类问题是可行的,且在缩短训练时间的同时不会降低预测准确率。

表1 实验1的软硬件平台速度比
(2)实验2。选取植物数据集(Iris data)中Irisversicolor和Iris-verginica共20个样本点作为训练数据,2类中剩余的80个样本作为测试数据。Iris-versicolor与Iris-verginica线性不可分,4个属性分别为sepal length、sepal width、petal length和petal width。核函数选择高斯核函数,sig2=2.25;γ-1=0.2。按照试验1的方法,将FPGA训练得出的α0, α1,…,α19、b值代入LS-SVM Matlab软件包对测试数据集进行预测,获得的结果如表2所示。其中,分类准确率达到96.25%,比LS-SVM Matlab软件包获得的分类准确率略高一些。从参数α的收敛时间看,FPGA的训练速度是LS-SVM Matlab软件包的运算速度的28.65倍。结果表明,串行结构的LSSVM FPGA实现架构同样可以很好地解决实验2的分类问题。可见,本文方法对解决线性不可分分类问题是可行的,且在缩短训练时间的同时还提高了预测准确率。

表2 实验2的软硬件平台速度比
结束语
本文研究了最小二乘支持向量机的FPGA硬件实现,完成了基于递归神经网络的LS-SVM串行FPGA结构设计。该结构具有串行计算、并行传输的特点。采用verilog HDL来实现该结构,设计者可以在编译阶段设置处理数据的字长,具有较强的灵活性。实验表明,与LS-SVM matlab软件包实现相比,基于递归神经网络的LS-SVM串行FPGA结构,能够准确地进行线性可分、线性不可分数据分类,并在速度上有一定的优势,验证了该硬件结构是可行、有效的,从而为LS-SVM在硬件平台上实现提供了一种思路。
10.3969/j.issn.1001-8972.2015.24.004

