基于ADAMS的连铸板坯摆式飞剪刚柔耦合仿真分析

张文强，罗会信，党 章，肖 腾，肖述池

（武汉科技大学机械自动化学院，湖北 武汉，430081）

连铸板坯摆式飞剪是现代连铸生产线的重要设备之一，其主要功能是对铸坯进行切头切尾以及将铸坯剪切成要求的定尺长度。在剪切时，摆剪的剪刃与铸坯之间要有较高的速度同步精度。传统研究［1－2］中，往往把摆剪作为多体刚性系统来进行分析，更侧重于理论层面，且研究工作多数以摆剪的动作控制分析为主。但是，把摆剪作为柔性体［3－4］来处理更符合实际情况，可以提高模拟精度以保证计算结果更为准确。为此，本文以某钢厂连铸板坯生产线摆剪为原型，运用多体动力学仿真软件ADAMS，建立以摆剪曲轴为柔性体的刚柔耦合虚拟样机，对其进行刚柔耦合分析，以期为飞剪产品的设计提供参考。

1 摆剪的结构和工作原理

该钢厂摆剪主要由上剪刃、下剪刃、摆动框架和驱动机构组成，其基本结构如图1所示。偏心轴的上剪刃曲轴和框架曲轴的夹角为180°。以摆剪传动主轴为中心点，上剪刃曲轴偏心距为70 mm，下剪刃曲轴即框架曲轴的偏心距为90mm，如图2所示。

在剪切板坯时，上剪刃在摆动框架的滑道内向下运动，下剪刃随摆动框架向上运动，同时摆动油缸带动摆动框架沿铸坯方向运动，并与板坯速度保持同步，当上下剪刃与板坯接触并作上下相对运动时实现对板坯的剪切［5－6］。

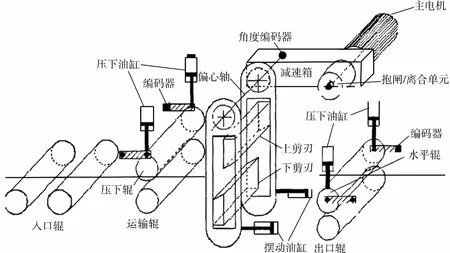
图1 摆剪结构图Fig.1 Structure of the pendulum flying shear

图2 摆剪偏心轴示意图Fig.2 Schematic diagram of the crankshaft

2 摆剪刚柔耦合模型的建立

2.1 多刚体模型的建立

采用Solidworks建立摆剪零件的几何模型，将模型文件（.x＿t格式）导入ADAMS中，添加运动副和约束，建立摆剪的多刚体几何模型，如图3所示。

图3 摆剪的多刚体模型Fig.3 Multiple－rigid－body model of the pendulum flying shear

2.2 刚柔耦合模型的建立

2.2.1 曲轴柔性体模型的建立

在HyperMesh中对曲轴进行建模及单元划分，共生成28432个六面体单元，单元类型为Solid45，网格图如图4所示。其中，曲轴与摆剪其他构件相关联的部件需要采用刚性连接处理，刚性连接区域定义了各铰点与相关节点间的力与位移的关系，以便在ADAMS中完成刚柔替换后实现运动与力的传递，关系式如下：

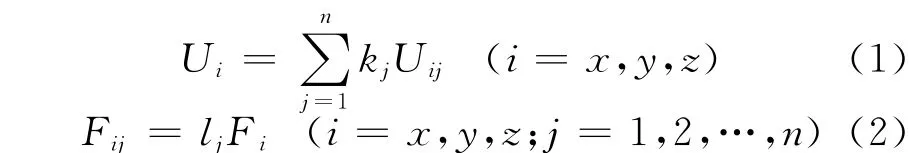
图4 曲轴的网格图Fig.4 Crankshaft grid

式中：Ui为刚性连接点的总位移；kj为j节点对总位移的影响系数，此系数与节点和刚性连接点的距离和角度相关；i为3个坐标方向；j为刚性区域从动节点数；Uji为j节点在i方向的位移；Fij为j节点在i方向的受力；lj为j节点对刚性连接点受力的影响系数，此系数与节点和刚性连接点的距离和角度相关；Fi为刚性区域在i方向的受力。

曲轴材料属性如表1所示。将模型导入Abaqus中计算得到模态中性文件（MNF文件），将此文件导入ADAMS中就可生成相应的曲轴柔性体模型。

表1 曲轴材料参数Table1 Material paramaters of the crankshaft

2.2.2 摆剪刚柔耦合模型的建立

在ADAMS仿真中，为了让剪切力更真实地传递，同时为了便于在ADAMS中添加载荷和约束，在HyperMesh中对直接受力部件（上、下刀刃）也进行离散化处理，并建立相应的刚性耦合单元，定义材料属性后分别导入Abaqus中计算得到相应MNF文件。将MNF文件通过RIGID TO FLEX方法导入ADAMS中，完成刚性体的柔性替换，参照文献［7］方法得到摆剪的刚柔耦合动力学仿真模型，如图5所示。

图5 摆剪刚柔耦合模型Fig.5 Rigid－flexible coupling model of the pendulum flying shear

3 添加驱动与载荷

3.1 曲轴及摆动液压缸驱动的添加

钢厂摆剪主要参数如表2所示。

在生产过程中，摆架的速度不仅要适应浇铸拉速，同时也要与曲轴转动角度相匹配，才能保证摆剪设备正常作业。在ADAMS中运用STEP函数来模拟曲轴驱动与摆动液压缸驱动，其中，曲轴驱动函数为

表2 摆剪主要参数Table2 Main paramaters of the pendulum flying shear

3.2 载荷的添加

本仿真忽略各部件之间的摩擦因素，取摆剪最大设计剪切力12400kN为系统负载来考察曲轴的变形与受力状况。根据实测的人字形剪刃剪切钢板时的剪切力变化规律［8］，用STEP函数近似替代真实受力变化，并将剪切力施加在上、下剪刃上面的相应节点上（在HyperMesh中设定的点集合），方向为垂直钢板表面，STEP函数具体设置如下：

上剪刃添加载荷函数

剪切90mm厚钢板时，上、下剪刃均接触到板坯的时刻为2.05s，故从2.05s开始加载，剪切力在2.35s时达到最大值12400kN，2.5s时板坯断裂，剪切阻力迅速消减为零，故仿真中摆剪的剪切时刻为2.05～2.5s。

4 仿真结果与分析

4.1 仿真可靠性验证

该钢厂连铸板坯摆剪正常工作时曲轴传动侧扭矩的实测值和仿真计算结果分别如图6和图7所示。对比图6与图7可以看出，曲轴传动侧扭矩的实测曲线和仿真曲线相似，扭矩均在剪切时刻达到峰值，扭矩峰值也在同一数量级上，实测及仿真计算所得扭矩峰值分别为5×108N·mm和7.57×108N·mm。虽然曲轴传动侧扭矩峰值的仿真值较实测值大了51.4%，但因为仿真时负载采用的是最大设计剪切力值，而实际生产中剪切力一般不会达到最大设计值，由此可以认为本次仿真的结果具有可靠性。

图6 曲轴驱动扭矩的实测值Fig.6 Torque of the crankshaft from field measurement

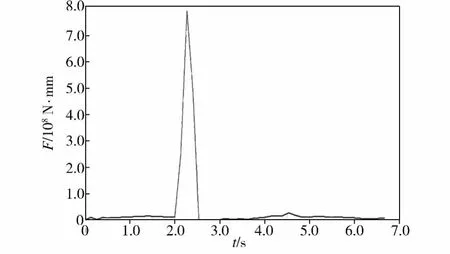
图7 曲轴驱动扭矩的仿真值Fig.7 Torque of the crankshaft from ADAMS simulation

4.2 曲轴上各连接处受力状况

剪切过程中曲轴上各连接处的约束力状况仿真结果如图8所示。由图8可以看出，曲轴上各连接处约束反力在剪切时刻（2.05～2.5s）随着剪切力的突然变化而增大，最大值达到6.8×106N，然后迅速衰减，表明摆剪系统危险时刻为其剪切力最大时刻。

图8 曲轴上各连接处受力图Fig.8 Force curves of each connection on the crankshaft

4.3 曲轴的动态应力分布结果

曲轴在剪切力最大时刻的等效应力分布图如图9所示。由图9中可见，应力较大区域位于上剪刃曲轴与下剪刃曲轴之间，最大等效应力值为100.4MPa。应力最大节点的等效应力时间历程曲线如图10所示，该节点主要承受剪切应力，在Hot plot table中查看Max Shear Stress可知，曲轴切应力最大值为66.4MPa。由旋转弯曲载荷作用下材料疲劳极限的经验公式［9］可得曲轴的疲劳极限为415MPa。根据第三强度理论，曲轴最大切应力远小于曲轴疲劳极限，在许用范围以内，满足生产需求。

图9 某时刻曲轴等效应力分布图Fig.9 Von Mises stress of the crankshaft at a certain time

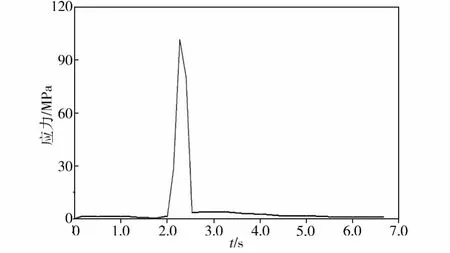
图10 应力最大节点的等效应力时间历程曲线Fig.10 Von Mises stress－time history curve of the node having maximum stress

4.4 曲轴的变形分析

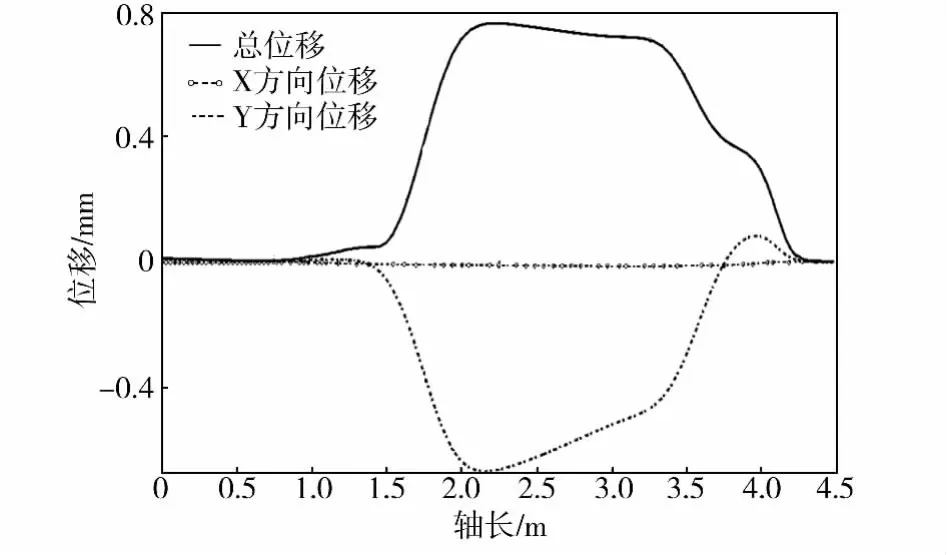
图11 曲轴轴承座中心线上各点位移图Fig.11 Deformation curve of nodes on the center line of the bearing seat of the crankshaft

曲轴沿轴向的变形如图11所示。从图11中可以看出，最大变形出现在曲轴轴承座中心线上距输入端2.2m的位置，最大变形量为0.78 mm，变形量较小，在正常情况下不会导致系统剪切故障。

5 结语

本文联合运用Abaqus与ADAMS对连铸板坯摆式飞剪进行刚柔耦合动力学仿真分析，得到了摆剪在剪切板坯过程中曲轴的受力及变形情况，通过与实测数据对比，验证了仿真结果的可靠性，可为摆剪的设计改造提供依据。仿真结果显示曲轴强度在许用范围内，曲轴的最大变形为0.78mm，满足生产要求，并且可以排除摆剪常见故障如因曲轴变形过大引起顶剪、上下刀架滑道铜板过度过快磨损等。本次仿真成功运用刚柔耦合虚拟样机技术，将有限元与多体动力学相结合，为复杂机构的设计分析及改造提供了一种方法，通过在ADAMS样机中改变机构的结构或参数来模拟现实状况，可以提高工作效率，降低生产成本。

［1］唐庆远，李慧剑.Z021－1摆式飞剪机构运动弹性动力分析［J］.振动与冲击，1990，9（1）：65－71.

［2］夏建芳.IHI摆式飞剪工作原理及剪切机构运动学模型［J］.中南工业大学学报：自然科学版，2001，32（6）：626－630.

［3］刘俊，林砺宗，刘小平，等.ADAMS柔性体运动仿真分析研究及运用［J］.现代制造工程，2004（5）：53－55.

［4］洪嘉振，蒋丽忠.柔性多体系统刚－柔耦合动力学［J］.力学进展，2000，30（1）：15－20.

［5］刘铁湘，林进江，程合喜，等.薄板坯连铸摆剪设备及改进［J］.连铸，2010（3）：38－39.

［6］周立宏.CSP摆动剪压下辊的故障分析［J］.安徽冶金，2006（4）：30－32.

［7］赵丽娟，马永志.刚柔耦合系统建模与仿真关键技术研究［J］.计算机工程与应用，2010，46（2）：243－248.

［8］刘才，李彤.摆式飞剪剪切过程弹塑性有限元模拟［J］.燕山大学学报，2003，27（2）：95－99.

［9］王国军.Msc Fatigue疲劳分析实例指导教程［M］.北京：机械工业出版社，2009：40－41.