含分布式电源的配电网可靠性评估

孙光远 李冬梅

（东北农业大学，黑龙江哈尔滨 150030）

含分布式电源的配电网可靠性评估

孙光远 李冬梅

（东北农业大学，黑龙江哈尔滨 150030）

采用改进的最小割集算法对含分布式电源的配电网进行可靠性评估。然后将分布式电源接入传统典型配电网，计算分布式电源接入前后可靠性的各项指标，分析不同数量、不同种类的分布式电源对配电网可靠性的影响。

分布式电源 配电网可靠性评估 最小割集算法

1 引言

本文采用改进的最小割集算法对含分布式电源的配电网进行可靠性评估。然后将分布式电源接入传统典型配电网，计算了分布式电源接入前后可靠性的各项指标，验证了分布式电源在改善电网可靠性方面的作用，同时分析了不同数量、不同种类的分布式电源对配电网可靠性的影响。

2 最小割集算法

最小割集法将计算限定在最小的范围之内，这样能够降低计算工作量。由于每个割集中的元件都是相互关联的，运用最小割集法时，首先要对最小割集进行确定，搜索出负荷点到电源点的供电路径。对于满足并联关系的割集内部元件，计算出并联系统的可靠性指标，公式如下：

式中：

UP为并联系统的年平均停电时间；

UEi为元件Ei的年平均停电时间；

rP为并联系统的平均停运持续时间；

λP为并联系统的故障率；

rEi为元件Ei的平均停电持续时间。

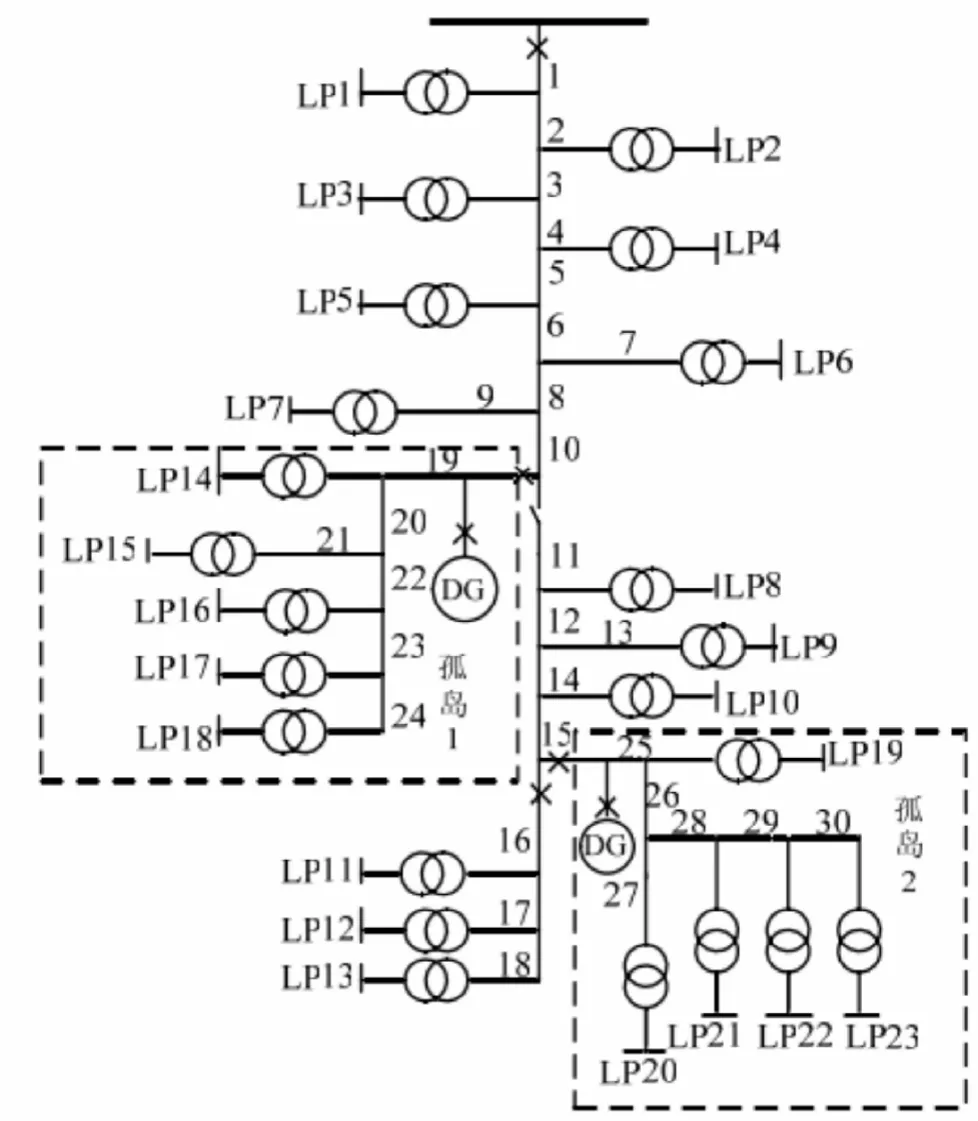
图1 含分布式电源的配电网接线

表1 方案一下的系统的可靠性指标

3 基于改进最小割集法的配电网可靠性评估

本章假设在负荷总量不超过发电总量时线路的潮流不会出现过载，即认为孤岛能够形成。由于负荷也是随时间变化，考虑到计算的精度和快速性，可以用文献［4］介绍的方法，将负荷分为10个等级水平，并计算出各个负荷水平出现的概率。由于DG发电量的不确定性和负荷的随机变化性，使得在发生故障后孤岛不能总是形成，孤岛的形成具有一定的概率性。

当发生上行故障时，孤岛形成的概率用公式表示为

式中

PIPLP为孤岛形成的概率；

PDGoutput为DG的发电量不小于某一负荷水平的累积概率；

Pload为负荷在某一水平的概率；

Pf为DG的故障率。

因此，由全概率公式可以得到，孤岛内负荷点LP的可靠性指标计算公式为：

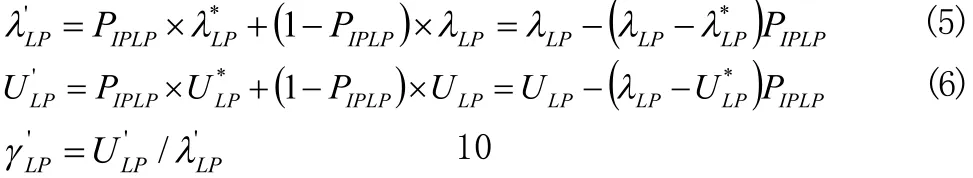
式中

λ'LP为孤岛范围内的负荷点的故障率；

U'LP为孤岛范围内的负荷点每次故障平均停电持续时间；

γ'LP为孤岛范围内的负荷点年平均停电时间；

λLP为配电网不带DG时负荷点的故障率；

ULP为配电网不带DG时负荷点的年平均停运时间；

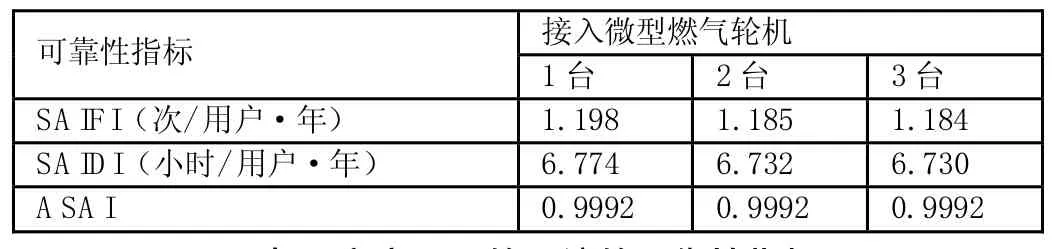
表2 方案二下的系统的可靠性指标

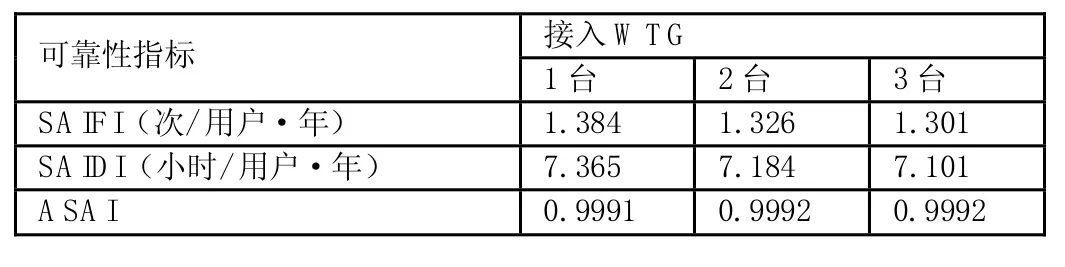
表3 方案三下的系统的可靠性指标

λ*为配电网带DG且孤岛能够形成时岛内负荷点的故障率；

LP

U*为配电网带DG且孤岛能够形成时岛内负荷点的年平均停

LP运时间。

对于孤岛外的负荷点，由于没有DG继续为其供电，因此可以按照传统配电网最小割集评估方法进行计算。

4 算例分析

4.1 算例

以IEEE-RBTSBus6系统主馈线F4为基础，在分支线19和25处加入2处DG。当上游供电路径发生故障时，通过断路器操作，形成孤岛1和孤岛2继续给岛内负荷供电，如图1所示。图中LPi表示第i个负荷点。

该系统有23个负荷点、1个隔离开关、23台配电变压器、4台断路器、23个熔断器（装设在负荷线路首端）。隔离开关操作时间为20分钟。

4.2 采用最小割集算法计算可靠性

运用本章提出的方法，对图1所示的配电网进行仿真计算，研究加入分布式电源前后对配电网供电可靠性指标的影响。

方案一：不考虑分布式电源的作用，计算出的负荷点可靠性指标，如表1所示。

方案二：设两处DG均采用微型燃气轮机，其故障率为4%，分别计算了1台、2台和3台微型燃气轮机后的可靠性指标（如表2所示）。

方案三：设两处DG均采用风力发电机组WTG，表3列出了这种方案下分别计算了加入1台、2台和3台WTG后的的负荷点可靠性指标计算结果。

从三种方案的可靠性指标计算结果可以看出：

（1）有DG和无DG的方案相比，DG的接入只对孤岛内的负荷点可靠性有影响，能使孤岛内的负荷点的故障率和年平均停运时间减小，并且显著提高系统可靠性。

（2）随着接入DG数量的增多，孤岛形成概率增大，负荷点的故障率和年平均停运时间降低，负荷点的供电可靠性提高。

（3）随着接入DG数量的增多，其对系统可靠性指标的改善程度逐渐变小，因此可以综合考虑经济成本、环境等各方面的因素，以决定DG的投运数量。

（4）程序的运行结果表明，该方法计算简单快速，但是欠缺灵活性，不能解决各种状态下的可靠性指标计算问题，例如若孤岛采用按等级切负荷措施以保证孤岛继续运行时，这种运行状态下的可靠性指标就无法计算了。

［1］黄伟，孙昶辉，吴子平，等.含分布式发电系统的微网技术研究综述［J］.电网技术，2009.33（9）：14～18.

［2］张勇，吴淳.分布式发电在配电网中的优化配置［J］.电力系统保护与控制，2010，38（11）：33～37.

［3］刘传铨，张焰.计及分布式电源的配电网供电可靠性［J］.电力系统自动化，2007，31（22）：46～49.

［4］杨文宇.基于最小割集的配电系统可靠性评估［D］.西安：西安理工大学，2002.