Design of a modern automatic control system for the activated sludge process in wastewater treatment

Alexandros D.Kotzapetros,Panayotis A.Paraskevas*,Athanasios S.Stasinakis

Water and Air Quality Laboratory,Department of Environment,University of the Aegean,University Hill,Mytilene 81100,Greece

Keywords:Activated sludge Modern automatic control PID controllers Root locus Waste treatment

ABSTRACT The Activated Sludge Process(ASP)exhibits highly nonlinear properties.The design of an automatic control system that is robust against disturbance of inlet wastewater flow rate and has short process settling times is a challenging matter.The proposed control method is an I-P modified controller automatic control system with state variable feedback and control canonical form simulation diagram for the process.A more stable response is achieved with this type of modern control.Settling times of0.48 days are achieved for the concentration of microorganisms,(reference value step increase of 50 mg·L−1)and 0.01 days for the concentration of oxygen(reference value step increase of0.1 mg·L−1).Fluctuations of concentrations of oxygen and microorganisms after an inlet disturbance of 5 × 103m3·d−1 are small.Changes in the reference values of oxygen and microorganisms(increases by 10%,20%and 30%)show satisfactory response of the system in all cases.Changes in the value of inlet wastewater flow rate disturbance(increases by 10%,25%,50%and 100%)are stabilized by the control system in short time.Maximum percent overshoot is also taken in consideration in all cases and the largest value is 25%which is acceptable.The proposed method with I-P controller is better for disturbance rejection and process settling times compared to the same method using PI controller.This method can substitute optimal control systems in ASP.

1.Introduction

Activated Sludge Process(ASP)is a biological process commonly used during wastewater treatment where microorganisms convert organic substances(substrate)to CO2and H2O via aerobic respiration as shown in reference[1].In its simplest form,ASP is consisted of an aerobic bioreactor(or aeration tank),where microorganisms participate in metabolic reactions degrading organic compounds,and a clarifier(or settler)where microorganisms are separated from treated wastewater via gravity.Treated wastewater is discharged from the upper part of the clarifier,whereas settled biological sludge is partly recycled from the settler to the bioreactor to maintain stable concentration of microorganisms and is partly wasted from the system for further treatment as shown by[2]and(Fig.1).

It is widely known that Wastewater Treatment Plants(WWTPs)often receive wastewater that presents significant daily and seasonal variations in in fluent flow rates.These variations may have negative effects on ASP performance and in some cases may result in process failure[1].Because of that,an advanced control system is necessary to make the process more robust in such variations,improving in parallel process' settling time.

So far,the majority of the systems that have been used to control ASP are based on P or PI controllers(classical automatic control)as shown by[3,4].Sometimes even PID controllers are used.Classical controller parameters' adjustment is done through compensation procedures using root locus and frequency response(if the process' model is known)or through Ziegler–Nichols method which requires termination of the system function until the adjustment is completed[5].In cases that only one ASP unit is available in a WWTP,the environmental pollution during parameter adjustment is possible.Other methods for parameter adjustment are through frequency–response analysis and Bode diagrams[6].The Ziegler–Nichols method calculates directly the necessary values for the parameters of PID controllers,while the Bode method evaluates the transfer function of the process.The second method has the advantage that there is no need to shut down ASP for adjustments because the adjusting signal‘from a sinusoidal generator’is applied during the normal operation of the process.However,the sinusoidal signal some times is a disturbance that has significant value and causes instability to the operation of ASP.All the aforementioned methods are applied to ASP through a Supervisory Control and Data Acquisition system(SCADA)as shown by reference[7].

Fig.1.Conventional activated sludge system.

Modern automatic control is a system that controls various processes.It uses the feedback of state variables that describe the process to control activated sludge system as shown by[6].Modern control has the flexibility to place the poles of a system in more desirable locations of root locus via the adjustment of its feedback gains(pole placement design)while classical control based on PID controllers cannot always fulfill this task through compensation procedure[7–13].

Regarding the obstacles that modern automatic control has to overcome,it should be mentioned that ASP is a non-linear process and it can not deviate much from its working point.If there is a large deviation,the process fails as demonstrated in references[5,6].The inability of state variables' measurement with precision,reliability and in real time is another significant obstacle as demonstrated by literatures[2,7].The designer of a modern control system,with state variable feedback in complex processes which stem from the combination of simpler sub-processes such as SOand XH,has the opportunity to enhance the quality of treated wastewater in a degree that is not possible with the multi-loop classical systems that are commonly used today[14–21].On the other hand,there is an optimal control such as the optimal regulator which is a complicated system and it is rarely implemented in WWTP.

The main objective of this study was to design a modern automatic control system which uses an I-P modified controller[5]for ASP that will achieve faster system response in reference value changes and smaller fluctuations oft he controlled variables to the disturbances of influent flow rate(increased robustness or lower sensitivity)than the same system but with PI controller.Through examination of control variable fluctuation in the transient response region,there is no saturation in its value.As mentioned above a comparison was performed between PI controller and I-P modified controller.That comparison was feasible because the two control systems had the same characteristic equation as it results from Mason gain formula and signal flow graphs(Figs.2 to 4).ASP was a second order system in this study,combining the oxygen and microorganisms subsystems.The control system was tested with step changes in reference values of SOand XHwhich were symbolized as SO,REFand XH,REFand in step change of the disturbance qFfor both SOand XH.A control-canonical form simulation diagram was used for the process and the controller was a modified I-P type with state variable feedback design(or pole placement design).The selected poles were−0.018,−200.0− 200.0·i and−200.0+200.0·i for SOand –8.0,–7.0+7.0·i and –7.0 − 7.0·i for XH.Modern control such as this one was not as effective as optimal control but it was simpler and it was not studied extensively for the control of ASP.Additionally oxygen subsystem was combined with microorganism subsystem,a combination which was usually avoided in other studies because of the large difference in the settling times of the two systems(SOin minutes and XHin days).This approach has advantages compared to isolated subsystems of SOand XHin both settling time and disturbance rejection.I-P controller is different from PI controller in that the proportional part of the controller is fed with the feedback variable and not with the error as it is done with the PI controller.This difference makes the system more robust.When in the reference input there is a step function change then the control signal of the closed loop system will have a step-like shape with overshoot.This is undesirable in many cases where a smoother response is required.By moving the proportional action of the controller in the feedback loop this acts only in the feedback signal and the step like control signal is omitted(Ogata[5]).So the controller I-P is also a PI type as it is shown in Fig.2 and the difference of I-P with the PI controller is the type of signal the two parts of the controller(proportional and integral)are fed with(error signal or feedback signal).From Fig.2 it is calculated that if the reference value is zero then for I-P controller:which is the transfer function of a PI controller.This calculation shows that if the reference value is zero then the I-P and PI controllers are identical.Changes in the reference values of oxygen and microorganisms(increases by 10%,20%and 30%)show satisfactory response of the system in all cases.Changes in the value of inlet wastewater flow rate disturbance(increases by 10%,25%,50%and 100%)were stabilized by the control system in short time.Maximum percent overshoot is also taken in consideration in all cases and the largest value was 25%which is acceptable.

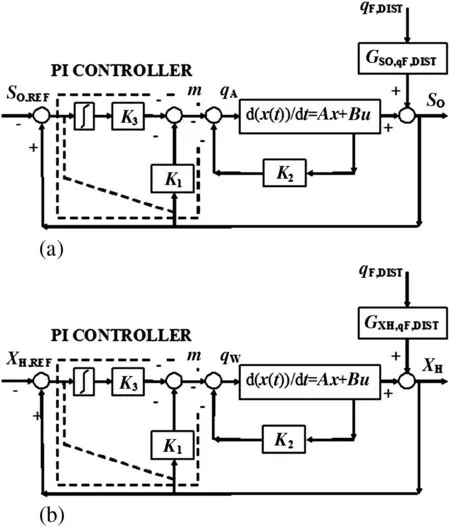
Fig.2.Modern automatic control system block diagram with disturbance for(a)oxygen and(b)microorganisms[6].

2.Proposed Modified I-P Controller Control System with Pole-Placement Design

An I-P controller control system or modified I-P controller control system with pole-placement design is the modern automatic control system used in this study.A more stable response is achieved with this type of modern control.The modern automatic control system is used as a single input and single output control system but with the feedback of all the state variables of the process which is controlled[6].The block diagrams of oxygen and microorganisms are presented in Fig.2.In Fig.3,it is shown how the process transfer function gives the simulation diagram of control-canonical form.Two control variables(qWand qA)are used by the I-P controller control system of this study as input control signals.

Comparisons between the systems presented in Figs.3(a)and 4(a)are easily done because they have the same characteristic equation according to Mason's gain formula.Also systems in Figs.3(c)and 4(b)have the same characteristic equation and can be compared.Similarly the signal flow graphs for the qFdisturbance can be drawn.Inlet flow rate(qF)value change is the external disturbance for the subsystems of SOas can be seen in Eq.(14)and XHas can be seen in Eq.(16).

Fig.3.Modern automatic control system signal flow graph for oxygen with I-P control and(a)reference or(b)disturbance value step change.Modern automatic control system signal flow graph for microorganisms with I-P control and(c)reference or(d)disturbance value step change.

The above block diagram(Fig.2)results in[6]:

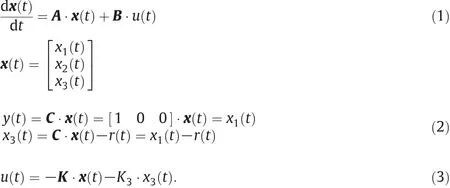
Substitution of Eq.(3)to Eq.(1)gives:

State variable x3(t)is adjoined to x（ t）in order to form the state vector of the feedback system xα（t）.The result from Eqs.(1),(2)and(4)is:

or

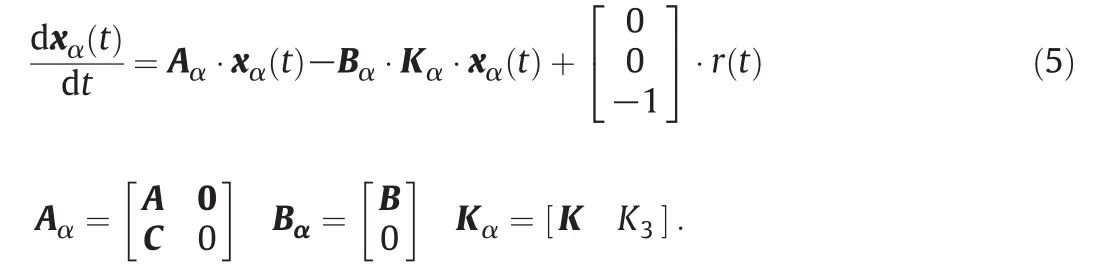
With Laplace transform the determinant or characteristic equation is calculated.Then this determinant is equated with the desired polynomial.The polynomial is the result of the pole-placement design(poles are selected to be in the appropriate regions of root locus and form the desired characteristic equation),and thus α0,α1and α2are known:

The coefficients in Eq.(6)can be equated to give three linear equations which define the values of K1,K2and K3.

3.Process Model

3.1.Model linearization

A simple model of ASP is used in the current study which is composed of three differential equations or mass balances of the substrate SS(Eq.(7)),oxygen SO(Eq.(8))and microorganisms XH(Eq.(9))as demonstrated by references[2,22]:

If it is assumed that the derivatives are zero,then the system of algebraic equations which arises gives the following working point(equilibrium point)values:XH=1121.0 mg·L−1(active biomass concentration),SO=2.079 mg·L−1and SS=4.213 mg·L−1.

If the system is in the working(equilibrium)point,then:

All the parameters used in these equations as well as their common values are reported in Table 1.For simplicity reasons,Eq.(7)is not used and it is assumed that SSFconcentration in the in fluent wastewater and SSin the bioreactor have steady values(Table 1 and working point values).As a result,if concentrations of microorganisms and oxygen are in acceptable levels,substrate consumption will also be acceptable.Inlet flow rate disturbance(qF)is placed in the same vector with the two control variables u.The above differential equations are nonlinear,and thus it is necessary to be linearized[6]and the transfer functions of the system are extracted after Laplace transform.In the working point of the system(system point of balance x0and u0),the following values can be calculated:from which matrices A and B can be defined:

and matrix C is:

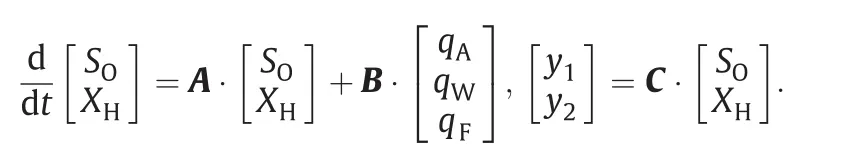
The Laplace transformation of the above equation yields:

In order to take SOopen loop transfer function with respect to qA,the control variable qWand disturbance qFmust be zero:

In order to take SOopen loop transfer function with respect to qF,the control variables qWand qAmust be zero:

In order to take XHopen loop transfer function with respect to qW,the disturbance qFand control variable qAmust be zero:

In order to take XHopen loop transfer function with respect to qF,the control variables qWand qAmust be zero:

From A and B matrices stems that the process' system is controllable and observable.In the above equations,x is a vector containing controlled or state variables that describe the ASP process,while u contains control variables qA,qWand the disturbance in fluent flow rate qF.In Eq.(11),the vector of output variables y1and y2is shown.State variables are SOand XH,while control variables are sludge discharge flow rate qWand air flow rate qA.It is important to mention that qAis used to control SOand qWfor XH.In addition,qAalso affects XHand qWaffects SO.It appears that ASP is a multivariable process as also shown by reference[23].It can be seen that all the above open loop transfer functions of the multivariable process have the same poles(same characteristic equation in the transfer matrix of Eq.(12)).There is a pole−0.15 close to the start of root locus,which stems from the subsystem of microorganisms with a slow transient response and a pole−84.034 which comes from the subsystem of oxygen with a fast transient response.In most studies it is avoided to combine these two subsystems due to the above characteristic.

3.2.Model simplifications

In the current study,it has been assumed that the clarifier is operated ideally achieving perfect separation of suspended solids from water,while the state variables are measured with precision,reliability and in real time.Finally in this study,automatic control has been applied only for organic carbon removal and not for the control of other biotic reactions observed in ASP process(biological nitrogen and phosphorous removal).

4.Control System Design Method

For the entire system(composed from the process model and the control system model)all system poles must lie in the desirable area of the root locus.The corresponding feedback gains for these poles are calculated.An appropriate area for pole placement is shown in Fig.5,[6,5,24].The stability,sensitivity and speed of response(settling time)of the state variables SOand XHin the system are adjusted by setting the poles in the right location.Settling time is a technical specification that describes the transient response of the system and should not be confused with the settling time of suspended solids in the clarifier via gravity.Another such technical specification is the maximum percent overshoot of the system.

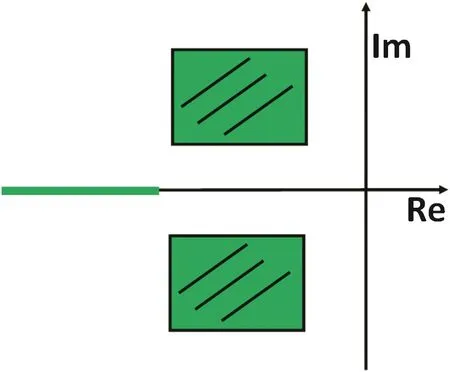
Fig.5.Suitable root locus areas for pole placement.(Im:the imaginary axis;Re:the real axis)

The a0,a1,b0and b1values for SOwith qAas a control variable are calculated from Eq.(13)and are used in the control-canonical form simulation diagram as shown in Fig.3(a):a0=12.589998,a1=84.184,b0=0.967086 and b1=53.727.The poles chosen for the system are−0.018,−200.0− 200.0·i and −200.0+200.0·i,and the K1,K2and K3values which result from these poles are:K1=−5.5734,K2=615.2769 and K3=1489.0.The pole−0.018 is chosen in order to deal with the problems that are faced in the transient response of the system(large overshoot)by the root of the numerator-0.018 which is the zero of the closed loop transfer Function(17).These problems stem from the difference in the transient response speed of the two subsystems SOand XH.It must be highlighted here that there is no cancelation or elimination of the transfer function's pole and zero and the system remains a third order system.The transfer function of oxygen concentration(SO)for I-P control(Eq.(17))for qA(control variable)is calculated from Mason's gain formula application in Fig.3(a):

It is shown here that the I-P's integrator increases the order of the system from the second to third.In PI control,the SOtransfer function is Eq.(18)for qA(control variable)and it is calculated from Mason's gain formula application in Fig.4(a):

The K1,K2,K3,a0,a1,b0and b1values are the same.Only the signal flow diagram changes‘Figs.3(a)and 4(a).

In the case of the qFdisturbance in SOand for I-P controller control K1,K2,K3,a0,a1,b0and b1are equal to the above values but the poles here are:−0.018,−200.0 − 200.0·i,−200.0+200.0·i,−0.15 and−84.034(Fig.3(b)the two last poles stem from Eq.(14)).The SOfor inlet flow rate disturbance qFhas the transfer Function(19)which is calculated from Mason's gain formula application in Fig.3(b):

The a0,a1,b0and b1values for XHand qWare(Eq.(15)):a0=12.589998,a1=84.184,b0=−14166.063626 and b1=−168.311.The poles that are chosen for the system(with pole placement design)are:−8.0,−7.0+7.0·i and−7.0−7.0·i.The K1,K2and K3values that are calculated for these poles are:K1=−0.013,K2=−64.372 and K3= − 0.055 ‘Mason's gain formula application in Fig.3(c)’.The transfer function of XHand I-P control for qWis Eq.(20):

The transfer function of XHand PI control for qWis Eq.(21)and it is calculated from Mason's gain formula application in Fig.4(b):

In the case of the effect of qFin XH,the values of K1,K2,K3,a0,a1,b0and b1are equal to the above values but the poles here are−8.0,−7.0+7.0·i,−7.0−7.0·i,−0.15 and−84.034(Fig.3(d)the two last poles stem from Eq.(16)).In I–P control,the inlet flow rate disturbance qFfor XHhas the transfer Function(22)and it is calculated from Mason's gain formula application in Fig.3(d):

It can be seen above that the feedback state variables are not only SOand XHbut also a combination of their derivatives(Figs.3 and 4).The two control systems are designed to control a multivariable process of combination of SOand XHbut they are functioning separately and isolated from each other(one controls SOand the other XH).

The response of the system to external disturbances in real time(inverse Laplace transform)is shown.The subsystems are subjected to step function input disturbances in the reference values of concentrations of oxygen and microorganisms,and in fluent flow rate.After this test which gives the stability,speed of the transient response(settling time as reported above)and sensitivity or robustness of the system,it is necessary to find the steady state response and the steady state error for step input function.State variables'(SOand XH)subsystems with I-P controller control have the same characteristic equations‘as it is calculated from Mason's gain formula’compared to that using simple PI controller.As a result,comparison of the two control systems is done simply by comparing their settling times.A system is bounded-input,bounded-output stable(BIBO),if,for every bounded input,the output remains bounded for all time.Sensitivity is the ratio of the percent change in the system transfer function to the percent change in a parameter(qF)of the transfer function.

5.Results and Discussion

For SO,the I-P modified controller control has lower settling time than PI control.The response of I-P is faster than that of PI and the reason for that is the selected poles of the closed loop system which are−200.0−200.0·i,−200.0+200.0·i and−0.018(−0.018 is canceled by the zero of the closed loop system).These poles give a response with high oscillation for PI controller which settles down slower than I-P controller.The purpose from the beginning was to prove that a control system with less oscillation can work better with two complex conjugate poles that are far from the imaginary axis.Margins are±5%of the value change and reference value is increased by 0.10(mg·L−1)by a step function(which is a 4.8%change), ‘Fig.6(a)and(b)’.In I-P,settling time is 0.01 days and in PI 0.02 days.The I-P control realization is used when it is not desirable to ‘bump’the plant with a step function as it is done in Fig.6(b)and PI controller.Maximum percent overshoot is 4%for I-P and 6%for PI controller.There is a value decrease in the start of oxygen system response with PI control.This is explained by the fact that K1has a negative value.The values of the feedback gains are K1=−5.5734,K2=615.2769 and K3=1489.0 so from Fig.4(a)it can be seen that when oxygen concentration reference value is increased by a step function the signal that is produced from the route with K1is negative.At the same time the signal from the route with the integrator is initially stable and increases gradually to make the control variable qAto have larger value than that in the beginning of the response and to increase SOconcentration.The reason for this gradual SOconcentration reduction in the start of the response is that the negative signal dominates and decreases qA.There was a gradual increase in oxygen reference value from 4.8%to 10%,20%and 30%.In the case of I-P control the only difference observed is the increase in the steady state value of oxygen concentration(as it was expected).Overshoot and settling time remain unchanged because the system has smoother response a common characteristic of I-P controller.In the case of oxygen reference value gradual increase and PI control there is a change in overshoot which is increased from 2%to 6%,and to settling time which is increased from 0.012 to 0.02 days.The steady state value of oxygen is also normally increased.The decrease in the start of the response is observed in all cases Fig.6.

Inlet flow rate disturbance has minor effects in oxygen concentration.A step increase of qFby 5(km3·d−1)causes initially a small decrease in oxygen concentration by 5.5× 10−4mg·L−1(the initial value of qFis 50 km3·d−1).The controller manages to reduce the error to zero as shown in Fig.7(a).This reduction of oxygen concentration stems from the increased dilution of oxygen because of the inlet flow rate which is larger.The disturbance percent change is 5/50=0.1 or 10%,while oxygen is disturbed no more than[(5.6×10−4)/2.079]=0.00026936 or 0.026936%.It is proven that the SOsystem with the I-P controller is adequately insensitive(robust)to the disturbance(this is of course a crude calculation of sensitivity).The transient response of the system in the qFstep change is slower than the transient response in reference value step change and this is caused by the pole−0.15.For the inlet wastewater flow rate disturbance there was a gradual increase from 10%to 25%,50%and 100%.This increase in the cases of oxygen and microorganisms gave an increase in their fluctuation but no change in the time interval required to enter the steady state(Fig.7).

Fig.6.Control for S O transient response in reference value step change of 4.8%to 30%for(a),(c)I-P controller and(b),(d)PI controller(dashed lines±5%of the value change and time in days(d)).

Fig.7.Effect of disturbance from 10%to 100%for(a),(c)S O and(b),(d)X H with I-P control.

Fig.8.Control for X H transient response in reference value step change from 4.46%to 30%for(a),(c)I-P controller and(b),(d)PI controller(dashed lines±5%of the value change).

Fig.9.Sludge wastage flow rate(q W control variable)value fluctuation for 4.46%reference value increase in(a)I-P and(b)PI control.

The concentration of microorganisms(XH)has lower settling time in I-P control than PI control.In I-P controller control,a reference value step increase of 50 mg·L−1in microorganisms' concentration has a settling time of0.48 days.This is 50.0/1121.0=0.0446 or 4.46%change for microorganisms.In PI control settling time is about0.6 days as shown in Fig.8(a)and(b).Maximum percent overshoot is zero for I-P control and 25.0%for PI control.There is a gradual increase of the microorganisms' concentration reference value from 4.46%to 10%,20%and 30%.For microorganisms' reference value gradual increase and I-P control no change is observed in settling time.There is no overshoot in any case.There is only an increase in the steady state value.For microorganisms' reference value gradual increase and PI control the results are the same with I-P control with the only difference to be that here there is an overshoot which is also unchanged Fig.8(c),(d).All the above are justified because the system's response speed does not depend from the magnitude of the step change.Fig.9(a)gives the fluctuation of the control variable qWin the transient response region for I-P controller(in XHit must be known how the control variable fluctuates since microorganisms define the substrate reduction in the wastewater which is the main purpose of the ASP).Fig.9(b)gives the fluctuation of the control variable qWin the transient response region for PI controller.From these two figures it is realized that there is no saturation on the control variable and that in I-P controller despite the fact that the control variable qWfluctuation is smaller it achieves lower settling time.Fig.9(a)and(b)stem from the control-canonical form part of diagram of Fig.3(c)and Eqs.(20),(21)and(23).The node from which K2gain is feedback is symbolized with J as shown in Fig.3(c).Also Fig.4(b)is used and then:

For the fluctuation of the control variable qWin the control of the microorganisms' concentration the superiority of I-P controller is shown.While PI controller value comes very close to the saturation value of zero in I-P there is a much larger margin and a lower settling time in the controlled variable of microorganism concentration.

The effect of inlet flow rate disturbance in the concentration of microorganisms is small for a step input increase of 5(km3·d−1).In I-P controller control,there is a drop of nearly 0.35 mg·L−1for concentration of microorganisms.This reduction of microorganisms' concentration stems from the increased dilution of microorganisms' because of the inlet flow rate which is larger.Then,the controller settles the error successfully as shown in Fig.7(b).The disturbance of qFis 5/50=0.1 or 10%,while XHis disturbed no more than(0.35/1121.0)=0.0003122 or 0.03122%.It is proven that the XHsystem with the I-P controller is adequately insensitive and robust to qFdisturbance.

Additionally,according to Figs.6,7 and 8 there is no steady state error in step inputs for all the above cases.These results are for comparison of the two control systems,I-P controller control and PI control,respectively,in the multivariable process of ASP.In a multivariable open loop system,all characteristic equations are the same.The slowest subsystem(XH)defines the response of the fastest subsystem(SO)(dominant poles).With pole placement design the pole that causes the slowest response can be chosen in such a way that it can be canceled with a zero as it is done with SOin the present study.Usually SOsubsystem alone has a settling time around 30 min,as shown by references[25–27].Settling time in XHas shown by references[2,28]is 5 days for a change of 850 to 1100 mg·L−1.So for both systems(SOand XH)the proposed control method achieves smaller settling times.

6.Conclusions

In this study,it was shown that the design of a high performance modern automatic control system which was stable,and insensitive(robust)in qFfluctuations,and had a low settling time was possible.I-P controller control was faster in XH,REFand SO,REFvalue step change and gave lower settling times than PI control.Disturbances in qFcould be handled without system failure.Moreover,there was no steady state error for all cases.Fluctuations of SOand XHvalues was very small in both cases(much smaller than the disturbance percent change),because of qFdisturbance,a result which exhibited system robustness.There was no saturation in the values of qW,which was used for XHcontrol.Additionally,oxygen subsystem was combined with microorganism subsystem,a procedure which is usually avoided in other studies because of the large difference in the transient response speeds of the two systems(SOin minutes and XHin days).As it is shown here,this approach has benefits in the settling time for both SOand XH.In this control system there was a combination of better performance and lower complexity,so as to be easier for the operators to adjust it.The proposed method takes into account the interactions between state variables in the multivariable process of ASP.It was an alternative control method to optimal control systems such as the optimal regulator which are rarely used and to other modern control methods.This study can be followed by experimental research that can confirm the simulation results.

Acknowledgments

The authors would like to thank Prof.C.Pilinis and Assistant Prof.C.Matsoukas for their helpful remarks.