基于改进EEMD的滚动轴承故障特征提取技术
魏永合,王明华,林梦菊,田 鹏
(沈阳理工大学机械工程学院,沈阳 110159)
基于改进EEMD的滚动轴承故障特征提取技术
魏永合,王明华,林梦菊,田 鹏
(沈阳理工大学机械工程学院,沈阳 110159)
在对集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)进行研究之后,提出了一种利用改进的EEMD进行滚动轴承故障特征提取的方法。该方法根据EEMD的分解过程中信号和加入的白噪声的特点来选择EEMD的参数,并且对分解后所得到的的固有模态函数(IMF)分量进行阈值处理后再重构,以降低噪声的干扰。对重构后的信号进行包络谱分析,提取其故障特征,最后将该方法与通用的EEMD方法进行对比,研究结果表明EEMD是一种很有效的滚动轴承故障特征提取方法。
集合经验模态分解(EEMD);滚动轴承;特征提取
0 引言
在机械工业领域中,旋转机械是使用最多的一类设备,而且通常状态下是负载大、连续工作的核心设备,非常容易发生各种故障而影响其正常运转,严重影响了质量和工作效率。而在各种旋转机器中,普遍应用的零部件便是滚动轴承,滚动轴承又是容易发生故障的零件,其安全与否,直接影响到机械设备系统的性能。滚动轴承的振动信号具有瞬态性和随机性,属于非平稳信号,因此使用传统的傅里叶变换不适合振动信号的分析[1],如果能够采用先进的信号分析技术,及时、无误的辨别出轴承故障信号的特征,必将为提高在工业领域应用较多的旋转机械的整体运行安全性和可靠性,避免意外停机和恶性事故。集合经验模态分解(EEMD)方法十分适合用于非稳定、非线性信号的分析[2-3],该方法是一种噪声辅助分析方法,通过在分析信号中加入一定白噪声,EEMD方法可以自动消除经验模态分解(EMD)存在的模态混叠问题。
1 EEMD的基本理论
经验模态分解(Empirical mode decomposition, EMD)方法能将信号自适应地分解到不同的尺度上,非常适合对于非稳定、非线性的信号进行处理[4],但其重要缺陷就是模态混淆现象的产生。所谓模态混叠,即一个IMF分量包含了特征的尺度差别较大的信号,或者为一相近尺度的信号显示在互相各异的IMF分量中[5]。
为降低EMD的模态混叠,Wu Z H等人在对白噪声进行EMD分解深入研究的基础上提出了集合经验模态分解(EEMD)[6]。EEMD是一种噪声辅助分析方法,通过在分析信号中加入一定白噪声,EEMD方法可以自动消除存在的模态混叠问题,该方法将所得到的EMD的IMF进行多次平均,从而得到最终的EEMD的IMF。EEMD方法能够将原始的时间序列分解成若干个不同时间尺度的序列,各个组分序列分别体现原始序列的局部化特性,每个组分的影响因子不同。分解得到的IMF分量的数量以及每个IMF分量的频率和振幅由时间序列本身决定。EEMD算法的分解步骤和原理如下[7]:
步骤1:对EMD的执行总数设定初始值M,加入的高斯白噪声系数k,m=1;
步骤2:进行第m次EMD试验:
(1)对输入的初始信号x(t)上加入高斯白噪声nm(t),得到加噪后的信号xm(t)
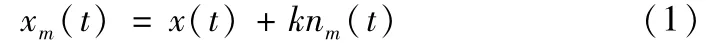
(2)采用EMD的方法分解xm(t),获得I个IMF cj,m(j=1,2,…I),cj,m为第m次试验分解的第j个IMF;
(3)若m<M,返回步骤2,m=m+1;
步骤3:计算M次试验的各个IMF均值
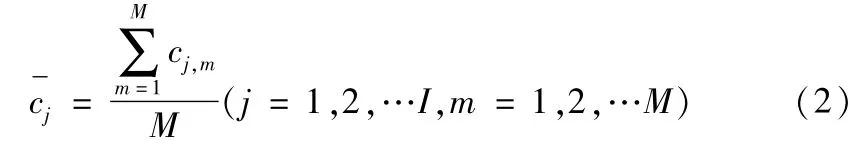
2 故障特征提取方法
试验所用轴承破坏性数据来自于美国凯斯西储大学轴承实验室,试验时分别在电动机端轴承的内圈、外圈和滚动体上使用电火花方法人为地加工了直径为0.021英寸的故障。将有故障的轴承重新装到电机上进行测试和记录振动数据,本实验所用的轴承型号为SKF6205-2RS。采样频率为12000Hz,采样点数为10000Hz。根据轴承的参数以及故障频率公式求得滚动轴承理论的内圈故障频率为157.94Hz,外圈故障频率为104.57Hz,滚动体故障频率为68.75Hz。
2.1 对数据进行小波去噪
在信号的采集和传输中,由于受外界干扰和本身设备的影响,不可避免的会有噪声掺杂在里面,而噪声对数据的准确性有重要的影响,所以在进行故障特征提取之前,需要先对原始信号用小波技术进行去噪,小波去噪主要分成以下三个步骤[8]:
(1)对观测数据作小波分解变化:
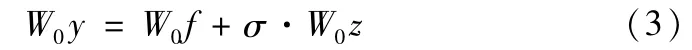
上式中y为观测到的数据向量y1,y2,…yn,f是真实信号向量f1,f2,…fn,z是高斯随机向量z1,z2,…zn。
(2)对小波系数W0作门限阈值处理,阈值形式为:

门限阈值处理可以表示为ηtn,可以证明当n趋于无穷大时使用阈值公式(4)对小波系数作软阈值处理可以几乎完全去除观测数据中的噪声。

2.2 EEMD参数设置
根据前面的EEMD理论对降噪后的数据进行处理得到I个IMF分量。由于EEMD是在EMD的基础上进行改进的算法,因此包含了EMD的全部优势[9]。但和EMD有差别的是,EEMD方法有两个参数必须在应用之前进行设定,也就是算法执行EMD的总次数M以及信号中加入的白噪声幅值标准差比值系数k。由于噪声对于分解结果的影响e(定义为输入与加噪分解后所有IMF和的标准差),与M、k有如下关系:

由式(6)可知,如果加入的白噪声幅值系数k相对信号来说幅值太小,将不会导致信号局部极值点发生改变。另一方面,当所加入的白噪声幅值系数过大时,就会导致分解出过多的IMF组成部分。通用的EEMD方法是根据经验人为选取参数,为了使分解结果更加准确,本文采用signal-to-noise(SNR)的方法来确定EEMD的参数,该方法的计算公式如下:
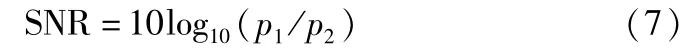
上式中p1为信号的能量,p2为噪声的能量,当所分析的信号的能量被确定之后,就可以确定加入的白噪声的能量,之后就可以求得加入白噪声的幅值。当SNR取50-60dB的时候可以取得较好的效果[10]。
对于重复试验的次数M,由于当加入的白噪声信号覆盖频率所在范围时,只有低频白噪声会对信号起作用,而高频不会,因此在进行正式分解之前,首先对信号进行傅里叶变换,获得其频率所在范围的上限,再根据这个频率上限对加入的白噪声进行滤波,这样就可以减少重复试验的次数。经多次试验表明,当重复试验次数M=70时,EEMD会取得较好的分解效果。滚动轴承的内圈、外圈、和滚动体的EEMD分解结果分别如图1、图2和图3所示。

图2 外圈有故障的轴承振动信号EEMD分解结果
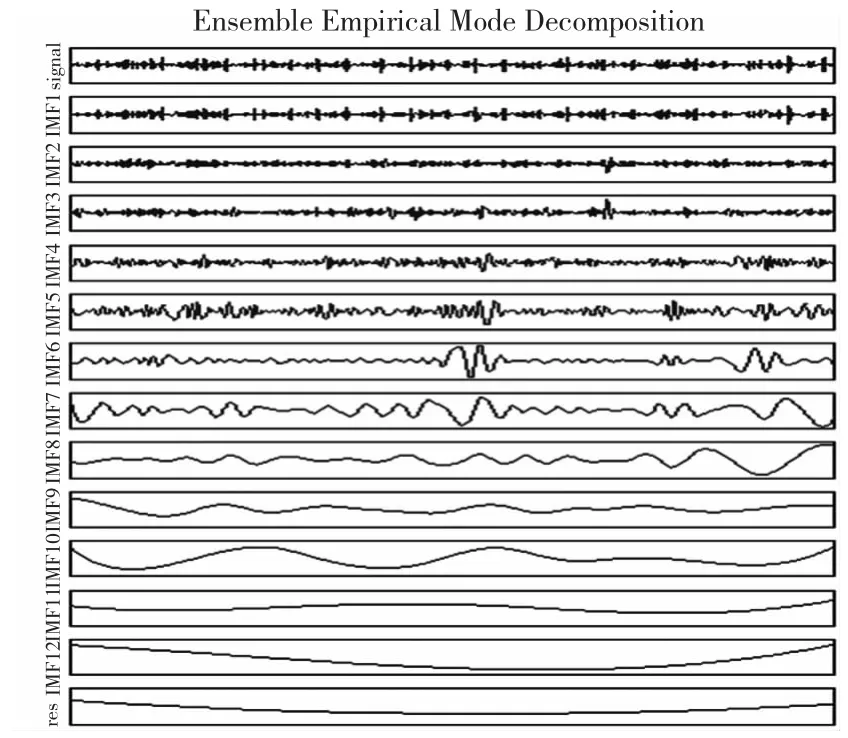
图3 滚动体有故障的轴承振动信号EEMD分解结果
2.3 固有模态函数重构
通用的EEMD方法只是根据经验设置参数,选择其中与振动信号相关性较好的IMF分量进行包络谱分析,但这会对振动信号的主要信息进行遗漏,而采用改进的EEMD方法,根据阀值选择IMF进行重构,则可以避免上述缺点,并有抑制噪声功能。
采用皮尔逊相关系数法得到各个IMF分量与振动信号的相关系数[11],公式如下:
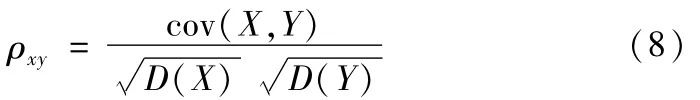
式中,cov(X,Y)为两序列的协方差,D(X),D(Y)为序列X和序列Y的方差,由此公式可以得到振动信号与IMF的各个分量cj的相关性系数αj。
相关系数越大的IMF,包含信息量越大。对滚动轴承的内圈、外圈和滚动体信号进行EEMD后,得到IMF分量的相关系数曲线如图4所示。

图4 IMF的相关系数曲线
之后采用阀值法去除与振动信号相关性特别小的伪分量,具体的方式是将各个IMF与振动信号的相关系数的最大者的十分之一设定为阀值。对信号进行EEMD分解后的分量进行重构,能在保留信号主要信息的条件下有效的消除噪声影响。由前面EEMD分解原理可知,所分解的IMF分量是从高频到低频的层层过滤,并且噪声信号主要集中在前面的几个分量中,所以可以考虑用从底层到顶层的细节重构(c-f)来对前面的经过阀值处理后的IMF分量进行重构。c-f的重构算法如下:
(1)将第n个IMF分量赋值给第1个c-f分量,即
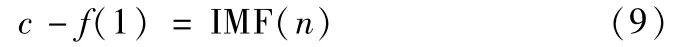
(2)对j=2:n而言,
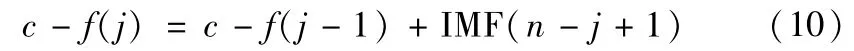
从而得到全部的n个c-f信号。
3 故障特征提取结果
对去噪后的内圈、外圈和滚动体的振动信号采用改进的EEMD法分解后所得到的IMF分别进行重构,再做包络谱分析,得到的包络谱与通用的EEMD方法的包络谱对比图分别如图5、图6和图7所示。

图5 滚动轴承内圈故障包络谱
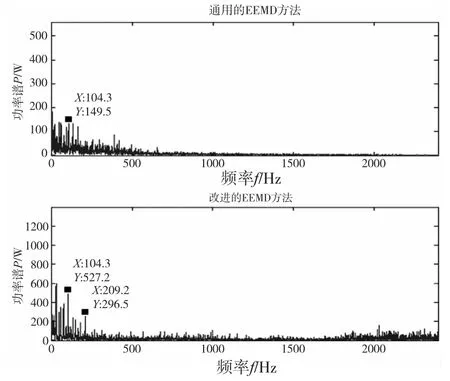
图6 滚动轴承外圈故障包络谱
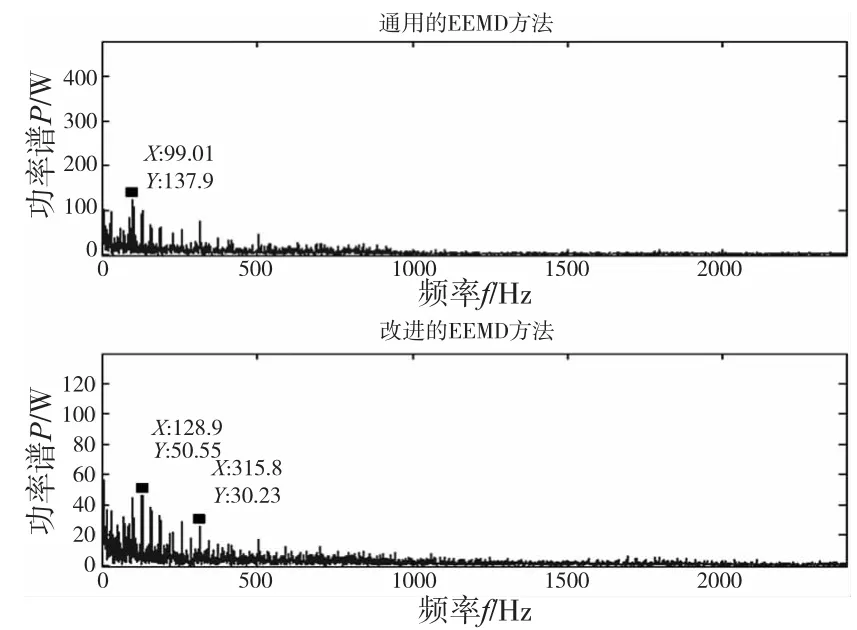
图7 滚动轴承滚动体故障包络谱
如图5所示,对于内圈故障,改进EEMD法的包络谱图中的故障特征频率相对于通用EEMD法更明显,与内圈的理论故障频率157.94Hz及其倍频很接近,误差在3%以内。对于外圈和滚动体故障,采用改进EEMD法进行故障特征提取的效果相对于通用的EEMD法有了较大的改善,图6所示的改进EEMD法的外圈故障包络谱中所提取到的故障频率与理论故障频率104.57Hz及其倍频也很接近误差也在3%以内;由于当轴承滚动体出现损伤时,其缺陷冲击滚道带有随机性,所以提取滚动体的故障特征比较困难,图7中采用通用EEMD法进行特征提取的效果很差,并没有提取到故障特征频率。但是采用改进EEMD法对滚动体的故障特征频率进行提取获得了很好的效果,理论故障频率68.75Hz的倍频很明显,误差较小。
4 总结
本文采用改进的集合经验模态分解(EEMD)方法对滚动轴承振动信号进行分解,根据加入的白噪声的特点来进行参数的设置,对于故障特征信息的提取更加准确。并且之后对分解后的信号重构再进行包络谱分析,抑制了噪声。最后与通用EEMD法进行对比,特征提取的效果有了改善,特别是对于外圈和滚动体故障,证明了采用改进EEMD法对滚动轴承的故障特征提取的可行性。
[1]高鹏磊,库祥臣.数控机床刀具磨损状态特征参数提取[J].组合机床与自动化加工技术,2013(6):65-67.
[2]王谨敦,陈略,曲卫.基于EEMD的故障微弱信号特征提取研究[J].电子设计工程,2012,20(14):72-74.
[3]任玥.基于Hilber t-H uang变换的滚动轴承智能诊断方法研究[D].成都:西南交通大学,2007.
[4]Huang N E,Shen Z,Long SR,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of theRoyal Society,1998,454(1971):903-995.
[5]曹冲锋,杨世锡,杨将新.大型旋转机械非平稳振动信号的EEMD降噪方法[J].振动与冲击,2009,28(9):33-38.
[6]Wu Z H,Huang N E.Ensemble empirical modedecomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[7]董文智,张超.基于EEMD能量熵和支持向量机的轴承故障诊断[J].机械设计与研究,2011,27(5):53-63.
[8]徐明林.基于小波降噪和经验模态分解的滚动轴承故障诊断[D].哈尔滨:哈尔滨工业大学,2013.
[9]窦东阳,赵英凯.集合经验模式分解在旋转机械故障诊断中的应用[J].农业工程学报,2010,26(2):190-196.
[10]Jian Zhang.Ruqiang Yan.Robert X.Gao.Zhihua Feng.Performance enhancement of ensemble empirical mode decomposition[J].Mechanical Systems and Signal Processing,2010,24:2014-2023.
[11]聂鹏,徐洪,刘新宇,等.EEMD方法在刀具磨损状态识别的应用[J].传感器与微系统,2012,31(5):147-152.
(编辑 李秀敏)
A Technology on Rolling Bearings Fault Feature Extraction Based on Improved EEMD
WEI Yong-he,WANG Ming-hua,LIN Meng-ju,TIAN Peng
(School of Mechanical Engineering,ShenYang Ligong University,shenyang 110159,China)
A method using improved EEMD to the feature extraction of rolling bearing is proposed,after research on Ensemble Empirical Mode Decomposition.This method select the EEMD parameters according to the characteristics of signal and the added white noise of EEMD.In order to reduce the interference of noise,through thresholding and reconstructing every intrinsic mode function.Then the envelop spectrum of the signal was analyzed,extracted the fault characteristics of the rolling bearings.Finally,comparing the method with universal EEMD method,the result shows that EEMD is a very productive method of fault diagnosis of rolling bearings.
ensemble empirical mode decomposition(EEMD);rolling bearing;feature extraction
TH165+.3;TG506
A
1001-2265(2015)01-0087-04 DOI:10.13462/j.cnki.mmtamt.2015.01.024
2014-04-16;
2014-04-26
魏永合(1971—),男,河北邯郸人,沈阳理工大学教授,博士,研究方向为先进制造技术、企业流程管理、设备管理和制造业信息化技术,(E-mail)yonghewe@sina.com。

