Fuzzy-PID知识库的优化及其IP核设计*
于世华,闫庆鑫,齐献伟,袭萌萌,郑佳硕,王开宇
(1.呼伦贝尔学院计算机科学与技术学院,内蒙古呼伦贝尔 021008;2.大连理工大学电子科学与技术学院,辽宁大连 116024)
Fuzzy-PID知识库的优化及其IP核设计*
于世华1,闫庆鑫2,齐献伟2,袭萌萌2,郑佳硕2,王开宇2
(1.呼伦贝尔学院计算机科学与技术学院,内蒙古呼伦贝尔 021008;2.大连理工大学电子科学与技术学院,辽宁大连 116024)
优化知识库是提高模糊控制性能的关键和难点,文章结合传统模糊PID控制规则与理论知识,重点优化了比例系数和积分系数的推理规则,并在Matlab/Simulink仿真平台进行验证。优化后的控制器具有更强的适应性和鲁棒性,对于典型二阶系统,在阶跃输入条件下,上升时间与峰值时间均减少8ms,超调量下降2.18%,进入±5%误差带调整时间减少105ms,在高频扰动或被控参数变化频繁的场合尤其重要。同时,为使该控制器灵活运用于SOPC系统级设计,文章运用Verilog HDL描述语言,采用模块化设计方法,模糊推理部分采用离线计算、在线查表的方式,PID算法采用改进的增量式并行结构,实现了基于FPGA的模糊自适应PID控制器IP软核,简化了系统设计,降低了FPGA资源耗费。测试结果表明,该控制器IP软核结果正确有效,可以灵活调用。
知识库;现场可编程门阵列;模糊PID;知识产权核
0 引言
随着被控对象复杂度的增加及对控制性能要求的提升,如今工业自动化市场呈现出集成化、网络化、数字信息化、智能化等发展趋势[1]。提高系统控制性能,一方面要对算法进行优化或改进,另一方面要采用更好的数字信息化技术[2]。利用现场可编程门阵列(FPGA),设计者可根据需要集成一个或多个RISC处理器、专用外设和硬件加速单元,做成一片上可编程系统(SOPC);而且,对频率和算法并行计算要求较高的系统可以进行全硬件电路设计;此外,FPGA也开始集成A/D、D/A等外设。利用FPGA进行智能算法(模糊控制、神经网络、遗传算法等)的实现和系统级设计的研究日益活跃[3-5]。FGPA在工业领域的应用正在从辅助性器件向功能器件转移。
本文从智能控制算法改进和数字化实现角度,完成了模糊PID智能控制器的优化和硬件实现。模糊PID控制技术可以同时满足静态指标和稳态性能的高要求,克服单独采用PID控制技术的动态特性较差和单独采用模糊控制精度较低的不足,达到满意的控制效果[6]。通过文献调研发现了模糊PID控制规则的不一致性,本文对控制规则进行了优化并验证了优化后的控制效果。此外,利用FPGA技术设计了优化后的控制器IP核。
1 模糊自适应PID知识库的优化
1.1 测试平台搭建
常规的增量式PID算法如式(1)所示:
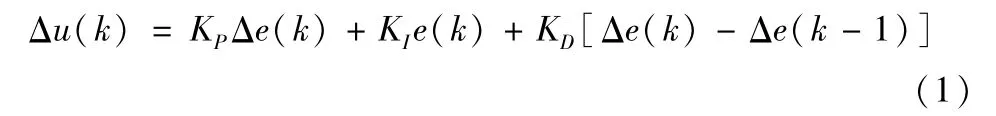
针对该PID算法,模糊自适应PID控制器的核心思想是:基于偏差E和偏差的变化率ΔE与PID三个参数之间的模糊关系,在系统运行过程中对E和ΔE实时检测,运用模糊推理对三个参数进行在线调整,以满足系统不同阶段的变增益控制需求,从而达到良好的动静态特性。
为测试控制器的效果,本设计选择典型二阶系统为被控对象,其系统传递函数如下:
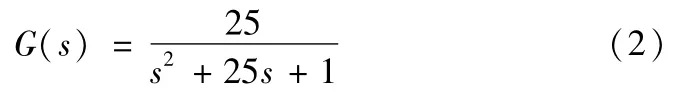
结合MATLAB中的Fuzzy Logic工具箱和Simulink仿真平台进行相应控制器的设计及控制系统的搭建。通过系统的阶跃响应曲线、偏差E及其变化率的实时曲线、PID三个控制参数经模糊推理后的增量变化曲线图等,来清晰地对比分析不同控制方式和优化前后的控制效果。
1.2 模糊控制器的设计及推理规则的优化
经过对系统控制精度和实现复杂度的权衡后,本设计对输入输出变量都进行了7级分割,偏差和偏差变化率的模糊论域均为{-3,3},ΔKp/ΔKi/ΔKd的模糊论域均为{-9,9},通过量化因子和比例因子来调节各变量物理论域与模糊论域之间的映射。语言变量为{PB,PM,PS,ZE,NS,NM,NB},即{正大,正中,正小,零,负小,负中,负大},PB隶属函数为S型,NB隶属函数为Z型,其他均为三角型。
模糊控制器类型为Mamdani,相应模糊逻辑算法选择如表1所示。

表1 Mamdani模糊逻辑算法
PID参数模糊自整定技术基于Kp、Ki、Kd各自的控制作用及其相互关系进行在线整定。综合考虑系统的稳定性、响应速度、超调量、稳态精度等性能指标,总结工程技术人员的知识和操作经验,人们对于参数选定总结了以下规则[7]:①若|E|较大时,为使系统有较快的响应速度,同时避免超调过大,应取较大的Kp,较小的Kd,并对积分加以抑制;②若|E|处于中等大小时,为保证系统的稳定性和较小的超调,应取较小的Kp,合适的Kd和Ki;③若|E|较小时,为使系统具有良好的稳态性能,同时避免系统在设定值附件出现震荡,应取较大的Kp和Ki,并取适当的Kd。综上,可以得出模糊规则表,多篇文献[6-8]中的模糊推理控制规则如表2所示。
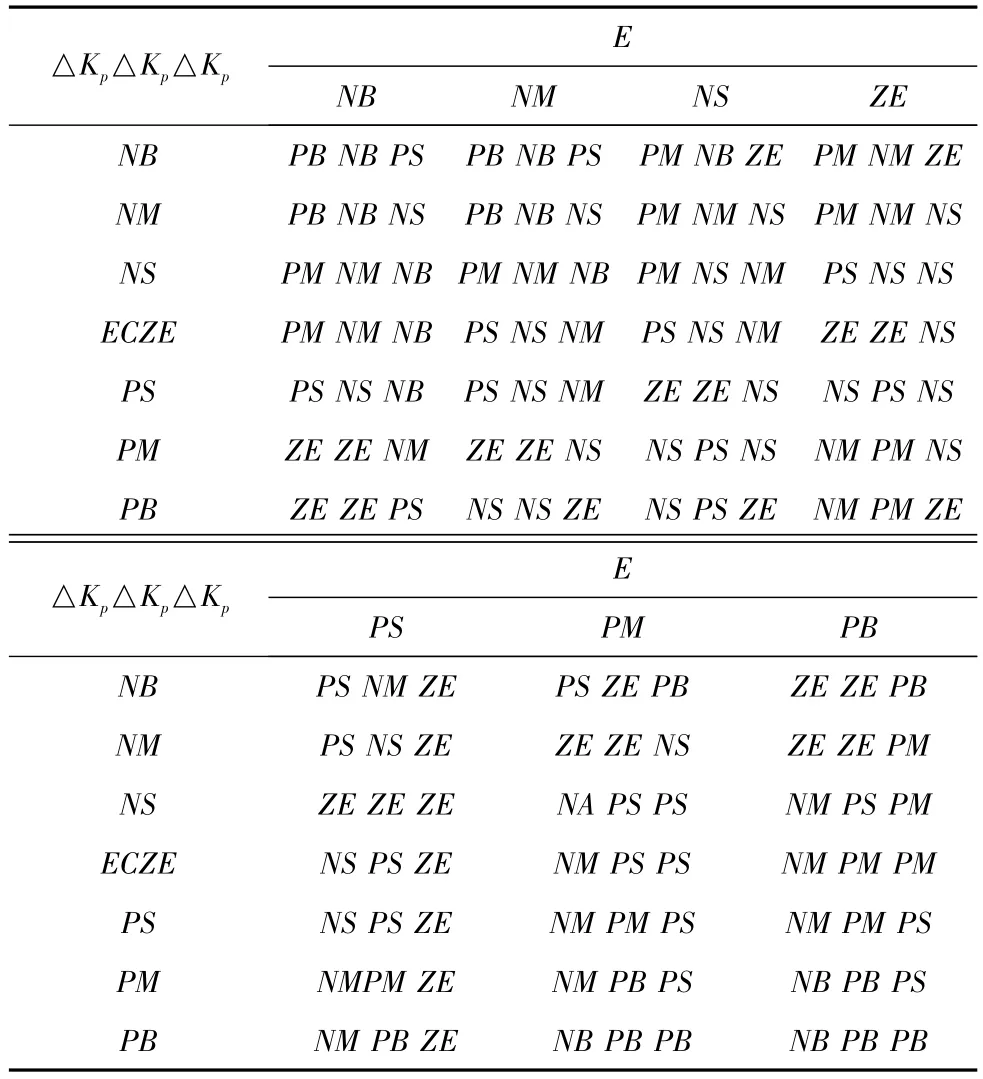
表2 优化前模糊PID推理规则表

图1 优化前控制参数在线调整规律
如图1所示,当偏差E比较大时,比例系数减少,积分系数增大;而偏差接近零和向负的方向继续增大时,积分系数仍在减少。最初偏差较大时,为了避免积分饱和,且保证系统的响应速度,积分系数应取较小值,比例系数取较大值。当系统出现超调,偏差为负,偏差变化率为也为负时,为尽快减少超调,应适当增大积分系数。因此,该控制规则推理结果不符合理论期望值。其中Kd变化曲线符合理论要求,于是本文主要对Kp和Ki推理规则进行优化。
基于文献[9-10]的启发,本文在传统控制经验的基础上,通过对文献中控制规则的测试及理论分析得出了新的模糊规则表。具体地,根据误差E和误差变化率DE的特征信息,分段对原控制规则进行优化。图2为典型二阶系统在阶跃输入条件下误差和误差变化率的响应曲线。

图2 典型二阶系统阶跃输入的偏差和偏差变化率响应
AB段,系统由零状态向稳定状态转变。起始阶段为使系统有较快的响应速度且避免积分饱和,Kp取较大值,并且对积分作用进行抑制;中间阶段,为保证系统稳定性,减少可能出现的超调,适当增加Kd值,并且减少Kp,Ki;接近B点时为使系统具有良好的稳态性能,同时避免系统在设定值附件出现震荡,应取较大的Kp和Ki,并取适当的Kd。BC段,系统出现超调且向增大的方向变化,此阶段应尽量压低超调,加大比例和积分控制作用,使得系统尽快回到稳态值。CD段,为防止系统回调,适当降低比例和积分作用,防止系统回调;DE段,系统误差在较小范围内正向增大,此时主要采用PI控制。所得优化后的整体控制规则如表3所示。
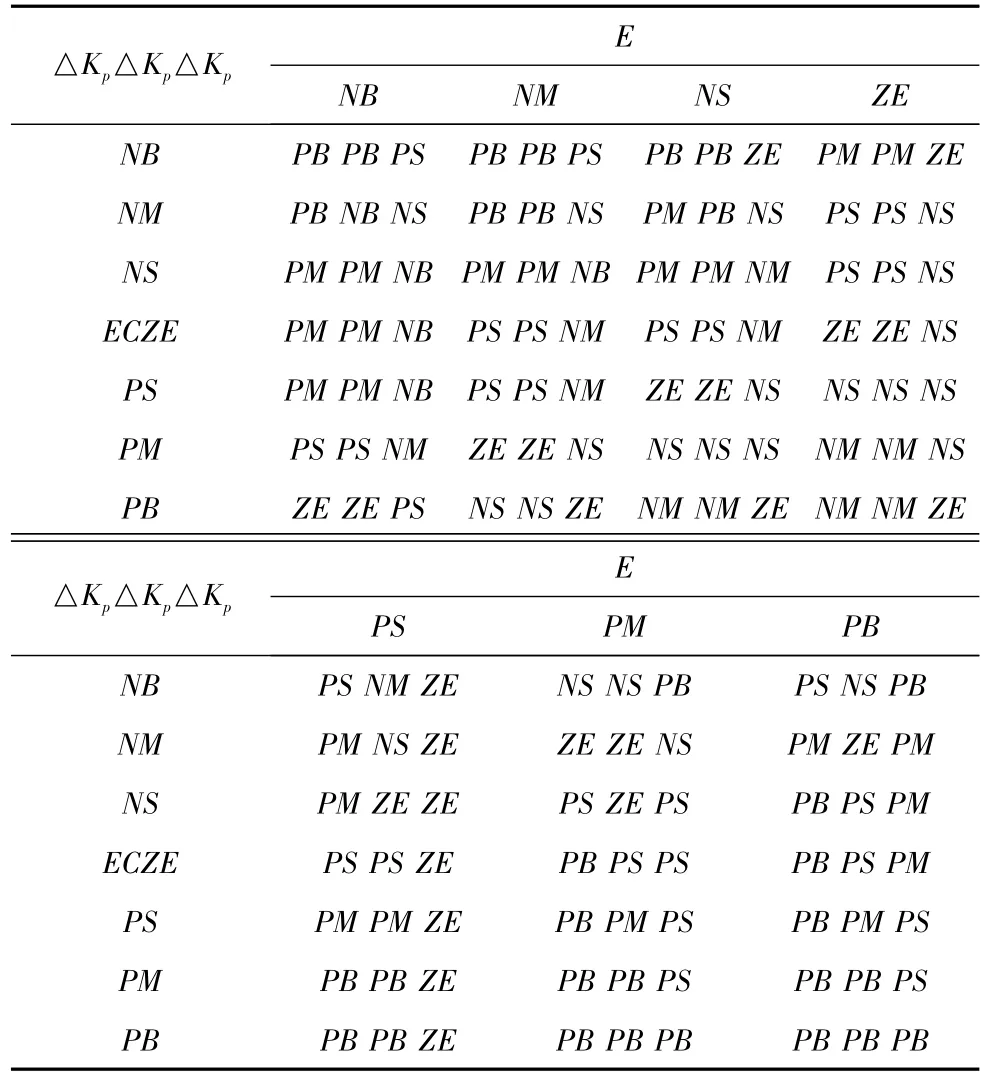
表3 优化后的控制规则表
图3是优化后控制规则对于典型二阶系统控制参数在线调整规律,图中各参数调整规律达到了期望效果,之后对其控制效果进行仿真测试。
1.3 结果分析
基于相同被控系统、量化因子、模糊论域、比例因子及参数初始值,本文在Simulink测试平台上对于优化前后的控制规则进行了测试验证,并与PID独立控制效果进行了对比分析。图4为阶跃输入条件下,三个控制系统的输出响应曲线。
对于三种控制效果,从上升时间、峰值时间、超调量和调整时间的性能指标角度进行对比分析,如表4所示。从图4及表4中可以看出,规则优化前的控制效果并不理想,而优化后的控制效果较优化前上升时间减少8ms,峰值时间减少8ms,超调量下降2.18%,进入±5%误差带调整时间减少105ms,对于控制性能实时性要求较高的应用场合具有较大的意义。

图3 优化后控制参数在线调整规律
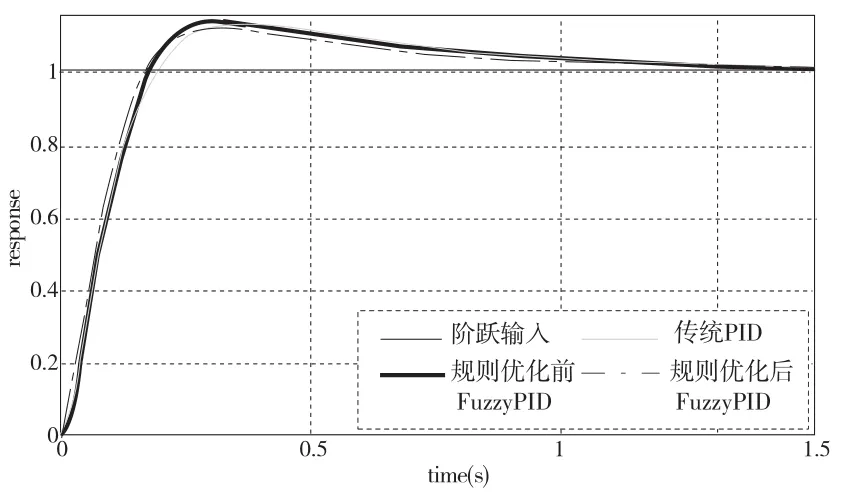
图4 三种控制方案控制效果对比图
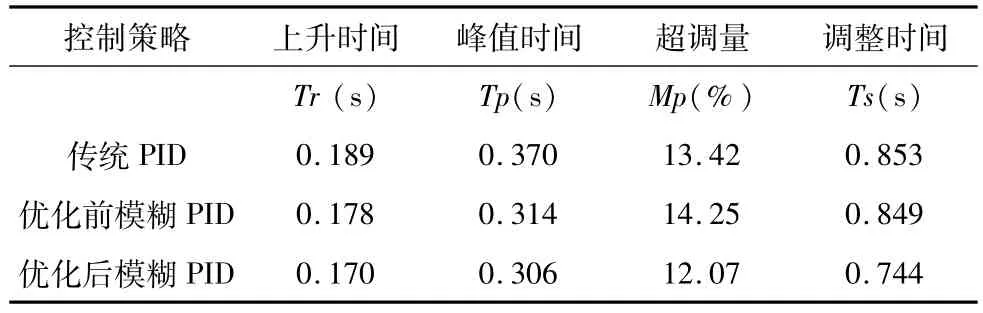
表4 三种算法控制效果对比分析表
2 Fuzzy self-turning PID的FPGA实现
该设计中核心部分仍为PID控制器,其硬件实现方式有串行、并行、混合、DA(分布式算法)等策略,鉴于并行实现结构较强的实时性,并充分利用FPGA的并行计算能力,本设计运用并行结构进行实现。
对(1)式进行整理化简得:
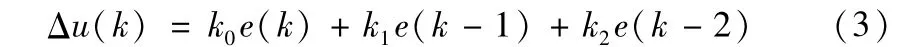
上式中,

因此实现该增量式PID算法,首先进行控制参数的线性变换,然后只需用3个乘法器和两个加法器即可完成计算过程。
对于模糊自适应环节,本设计采用离线计算、在线查表的方式实现。首先设计存放三个控制参数增量变化量的ROM表,将优化后的模糊控制器在Matlab/ Simulink环境下生成的模糊推理数据导入相应ROM表中,通过查找ROM表代替整个模糊自适应过程。该方法简化了模糊推理过程,加快了控制器的运行速度,缩短了开发周期。
本文在Xilinx ISE 14.1开发环境下,用Verilog HDL硬件描述语言,基于自顶向下的Top-Down设计思想,完成了该IP核的设计,其内部硬件结构和状态机模块分别如图5、图6所示。
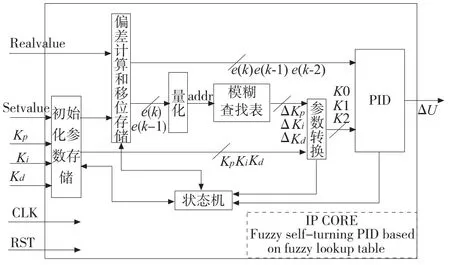
图5 模糊自适应PID控制器IP核的内部结构图

图6 状态机模块状态转换图
该状态机采用独热码编码方式实现,共包括六个状态(idle、st0~st4),其中Done信号为各状态的结束标志。
状态idle为复位状态,当复位信号RST出现下降沿时系统复位,复位结束后状态转入st0;状态st0完成初始化参数(如图8所示,包括期望值Setvalue、三个被控参数的初始值Kp、Ki、Kd),结束后状态转入st1;状态st1完成实际值Realvaue的采样和偏差计算及存储功能,输出量为最近三次偏差值(e(k)、e(k-1)、e(k-2)),完成后进入状态st2;状态st2为完成模糊推理的过程,包括利用e(k)和e(k-1)进行偏差变化量Δe(k)的求取,及e(k)和Δe(k)的量化,并通过量化所得的地址变量add进行查表输出三个控制参数增量的过程,该部分为纯组合逻辑,下一个时钟周期进入状态st3;状态st3进行参数转换,得到(3)式中对应的k0、k1、k2,结束之后状态转换至st4;状态st4实现增量式PID控制算法的并行计算,并且完成对输出的更新,结束后转至状态st1,进入下一个循环周期。
最后通过编写测试向量,结合Modelsim 10.1b仿真软件,得到了图7所示的功能仿真波形图。通过时序分析,该设计的结果符合设计思路,达到了预期效果。

图7 模糊自适应PID IP核功能仿真波形图
3 结论
针对文献中模糊自整定PID控制算法推理规则的不一致性性,综合分了析专家经验和理论知识,利用MATALB Simulink对推理规则进行了优化,结果表明优化后规则的控制效果在响应时间、超调量、调整时间等性能指标上都优于原规则的效果,能够使控制器拥有更强的适应性和鲁棒性。
优化效果验证后,本文以FPGA为硬件实现平台,设计了优化后的模糊PID控制器的IP核,并通过仿真验证了其功能的正确性,可以应用于实际控制场合。
[1]陆楠.创新FPGA平台环境针对工业应用[J].电子技术设计,2013(2):19-20.
[2]Leong,P.H.W.Recent Trends in FPGA Architectures and Applications.Proceedings of the Forth IEEE International Symposium on Electronic Design,Test&Application[C]. Hong Kong,2008:137-141.
[3]Kravets,P.I.,et al.,Methods of hardware and software realization of adaptive neural network PID controller on FPGA-chip[J].Journal of Automa-tion and Information Sciences,2011,43(4):70-77.
[4]Suratia,P.,et al.FPGA based Fuzzy Logic Controll-er for plasma position control in ADITYA Tokamak[J].Fusion Engineering and Design,2012,87(11):1866-1871.
[5]Somsubhra Ghosh,Ranjit Kumar Barai,et al.An FPGA Based Implementation of a Flexible Digital PID Con-troller For a Motion Control System.International Conference on Computer Communication and Informat-ics[C].Coimbatore,INDIA,2013:1-6.
[6]黄霞.基于FPGA的智能温度控制系统的设计[D].武汉:武汉理工大学,2012.
[7]刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2011.
[8]石辛民.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2008.
[9]Basil Hamed,Moayed Al-Mobaied.Fuzzy PID Controllers Using FPGA Technique for Real Time DC Motor Speed Control[J].Intelligent Control and Automation,2011,2:233-240.
[10]Wen Chen,Huimei Yuan,Yan Wang.Design and Implem-entation of Digital Fuzzy-PID Controller Based on FPGA.Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications[C].Xi'an,P.R.China,2009:393-398.
(编辑 李秀敏)
Optimization of Know ledge Base in Fuzzy-PID Controller and the Design of IP Core
YU Shi-hua1,YAN Qing-xin2,QI Xian-wei2,XI Meng-meng2,ZHENG Jia-shuo2,WANG Kai-yu2
(1.School of Computer Science and Technology,Hulunbuir College,Hulun Buir Inner Mongolia 021008,China;2.Department of Electronic Engineering,Dalian University of Technology,Dalian Liaoning 116024,China)
Optimization of Know ledge Base is key and difficulty to improve the performance of fuzzy control. This paper adjusts and optimizes the inference rules of proportionality and integral coefficient of fuzzy PID controller by combining the theory analysis with conventional inference rules.Then it was tested on the simulation platform of MATLAB/SIMULINK.And it proves that the optimized controller has better robustness and adaptability than the previous one.For a typical second order system with a step input,the rise time and peak time was both reduced by 8ms,the overshoot by 2.18%and the setting time(±5%)by 105ms which is vital in the occasions containing high frequency disturbance and frequent changes of the parameters.Meanwhile,the Fuzzy self-turning PID IP(Intellectual Property)Core based on FPGA(Field Programmable Gate Array)was implemented by using Verilog HDL and modular design method,to make it be flexibly used in system design based on SOPC(System on Programmable Chip).In this core designing,the modified incremental PID algorithm was used,and the part of fuzzy self-turning was replaced by on-line look-up table structure and off line inference,thus simplifying this design and reducing the hardware resources.The simulation results shows that the IP core can achieve correct and effective results and can be flexibly called.
know ledge base;FPGA;fuzzy PID;IP core
TH166;TG659
A
1001-2265(2015)01-0042-04 DOI:10.13462/j.cnki.mmtamt.2015.01.012
收稿日期:2014-03-28;修回日期:2014-05-06
中央高校科研基本业务项目(DUT13LAB17)
于世华(1972—),女,山东莱州人,呼伦贝尔学院副教授,硕士,研究方向为图像处理,模糊自动控制,(E-mail)ftdu@sohu.com。通讯作者:王开宇,(1973—)男,吉林榆树人,大连理工大学副教授,硕士,研究方向为硬件加密技术,(E-mail)wkaiyu@dlut.edu.cn。

