Application of pH control to a tubular flow reactor

İ.Halil Vural,Ayla Altinten *,Hale Hapoğlu ,Sebahat Erdoğan Mustafa Alpbaz

1 Ankara University,Faculty of Engineering,Department of Chemical Engineering,Tandogan,Ankara 06100,Turkey

2 Gazi University,Faculty of Engineering,Department of Chemical Engineering,Maltepe,Ankara 06570,Turkey

Keywords:Tubular flow reactor pH control Self tuning PID control PID control Fuzzy control

ABSTRACT Tubular flow reactors are mainly used in chemical industry and waste water discharged units.Control of output variables is very difficult because of the existence of high dead-time in these types of reactors.In the present work,sodium hydroxide and acetic acid solutions were sent to the tubular flow reactor.The aim was to control pH at 7 in the nonlinear region.The pH control of a tubular flow reactor with high time delay and a highly nonlinear behavior in pH neutralization reaction was investigated experimentally in the face of the various load and set point changes.Firstly,efficiency of conventional Proportional-Integral-Derivative(PID)algorithm in the experiments was tested.Then self-tuning PID(STPID)control system was applied by using the ARMAX model.The model parameters were calculated from input-output data by using PRBS signal as disturbance and Bierman algorithm.Lastly,the experimental fuzzy control of pH based on fuzzy model was achieved to compare the success of fuzzy approach with the performance of other control cases studied.

1.Introduction

In chemical engineering,processes are conducted for various purposes,some of which are for the production and separation of products.However,processes are defined with input and output variables in control studies and their design is based on these parameters.All the variables of this type of processes are constant with time under operating conditions and the system is at steady state.Some deviations may be observed due to some load effects in the course of the operation.Process control systems are applied in order to eliminate such disturbing effects and achieve optimum operating condition.

In literature,tubular flow reactors,which operate on the basis of piston flow,are favored as the best designed ones among the wastewater treatment systems because the chemicals are in good contact with the wastewater throughout the reactor and thus they help to save energy.The pH control is vitally important in the production of fatty acids,soap and medicine as well as in waste water treatment.The pH neutralization process is known as a difficult one because of its nonlinear dynamic properties.

Several dynamic mathematical models of pH systems are available in literature.Gustafsson and Waller[1]investigated adaptive pH controland dynamics of acid base reaction in a continuously stirred tank reactor.A number of controlling algorithms among which are linear based model,nonlinear internal control and nonlinear general models have been applied to pH control.Kulkarni et al.[2]applied nonlinear internal model controller(IMC)in single input-output(SISO)systems in which strong base and acid reactions were conducted.Wright and Kravaris[3]developed a new method for nonlinear controller for pH processes and a general nonlinear dynamic model consisted of chemical equilibrium reactions and material balance.Minim and Filho[4]defined tubular flow reactors as systems with nonlinear complex dynamic characteristics and as uniform time varying systems.Henson and Seborg[5]developed an adaptive nonlinear control strategy for a semipilotscale pH neutralization process and tested this strategy experimentally.Palancar et al.[6]applied a model predictive adaptive control system in a continuously stirred tank reactor for pH neutralization in wastewater containing acetic acid,prophyonic acid and sodium hydroxide.Bharathi et al.[7]performed an application of model based control systems to highly nonlinear systems such as pH controlled fed-batch reactors.Traditional PID controllers were far from giving efficient pH control in such processes because of their extra nonlinear features.It is proved with the simulation results in this paper that model based PI controller is superior in the performance and robustness to traditional PI controller.Gomez et al.[8]made Wiener model identification and developed a predictive model for pH neutralization process.They utilized the identified Wiener model as an internal model in a model predictive controller(MPC)and compared the performance of Wiener model predictive control(WMPC)with that of a linear MPC and PID controllers.The simulation results revealed that WMPC,linear MPC and PID controllers had better performance.Altinten[9]carried out generalized predictive control(GPC)in a pH neutralization process.This process consisted of a continuous tubular reactor.In the study,polynomial autoregressive integrated moving average with external input(ARIMAX)was used and the model parameters were determined by Bierman and Genetic algorithms.Efficiency of GPC in the experiments was tested by calculating the integral of the square of the error(ISE)and the integral of the absolute value of the error(IAE).Balasubramanian et al.[10]proposed a neural network(NN)based adaptive interaction technique for the development of a nonlinear pH controller.Meenakshipriya et al.[11]tested a proportional-integral-plus(PI-P)control strategy based on the coefficient diagram method(CDM)with a pH neutralization system.Simulation results showed that the CDM-PI-P controller had a good performance when compared to other techniques.

Fuzzy control has a wide range of industrial applications.Control rules and membership functions on fuzzy control are generally determined by trial and error method.Contrary to classical controller,fuzzy controllers are more capable of adopting information gained through human experience and they are more significant and convenient in dealing with control problems whose mathematical modeling is really hard and operation is expensive.The difficulties in the application may arise from nonlinear characteristic of processes,time-varying nature of the process to be controlled,unpredicted environmental effects,poor sensitivity of sensors and from the difficulties in making reliable and correct measurements.Technical knowledge of the experienced operator may serve as an alternative to the process model in overcoming such difficulties.Although it is not easy to formulate this knowledge with correct terminology,the operator can give a linguistic definition of the control behavior.This linguistic definition consists of a set of control rules derived by means of fuzzy method[12].Kelkar and Postlethwaite[13]stated that nonlinear characteristics of pH processes obstructed the application of classical control systems and they achieved to control the pH of strong base-weak acid neutralization reaction in a continuously stirred reactor using fuzzy based pH control.Wang et al.[14]suggested fuzzy model-based nonlinear internal model control(FNIMC)for pH neutralization process control.Sousa et al.[15]reported that fuzzy models represent highly nonlinear processes and integration of the predefinitions can be achieved by the information gained through process data.Altinten et al.[16]designed fuzzy control using genetic algorithms(GA)based on the natural selection principle of evolution.They built fuzzy membership functions and a relevant relation matrix using GA.They tried to control the temperature of a water-jacketed batch reactor,in which a free radical polymerization reaction of styrene takes place,by means of the system they designed.İbrahim and Murray Smith[17]designed a system for cloudy water for a pilot scale plant with industrial standards.The tests they performed yielded satisfying performance in terms of both steady state and transient characteristics.Chen et al.[18]studied on pH neutralization process and designed a robust control system Fuzzy Sliding Mode Control(FSMC)which combines the fuzzy control and sliding mode control.They used this control system in multivariable pH neutralization reaction.

The present study dealt with the pH control of a neutralization process with weak acid-strong base input in a tubular reactor.Base flow rate was chosen as the manipulated variable.Control of the pH was harder because there was time delay in addition to nonlinear characteristics of pH neutralization processes[19].As is known,PID controller has a linear nature.Tuning parameters of this controller are not changed when the operating conditions alter,but then a lot of characteristics of the process are changed.If the changes are small,then PID can perform a good control within most of the measurement range.Any change made in the value of concentration of acid,base and buffer solution in neutralization reactions may result in a highly nonlinear behavior in pH.This nonlinear behavior is also experienced when the feeding flow rate is changed during such reactions in continuously stirred reactors.For this reason an advanced strategy is required to control such a nonlinear behavior.In the present study,self tuning PID and fuzzy control strategies are proposed.In the evaluation of control efficiency,integral square of error(ISE)and integral of absolute value of error(IAE)are utilized.

2.Control Strategies

2.1.Conventional PID control based on linear model with nonparametric system identification

Conventional three term controllers employ proportional,integral and derivative control actions.

Various combinations of the three fundamental control actions involve their specific advantages and disadvantages.The PID controller is the most utilitarian of all the different combinations of control action.Three term control action can be described quantitatively by:

where Δ M is the variation in the controller output.

The performance of a PID controller depends upon the selection of a suitable sampling interval as well as on the correct tuning of KC,τIand τD.Different methods of controller tuning such as Cohen-Coon,Yuwana-Seborg and Jutan-Rodriguez for open-loop and close-loop systems are used.

2.2.Self-tuning PID control based on linear model with parametric system identification method

Self tuning control mechanism consists of a parameter estimator and automatic control systems.In this sort of control first a linear model is built for the system to be controlled.Structure of this model is defined with polynomial degree of the parameters.

The control equation is given as follows[20]

where r(t)represents the set point,and:

The system transfer function is given as

Self-tuning PID control algorithm may be given as follows:

(1)Apply a pseudo random binary sequence(PRBS)to the system as a forcing function and attain the plant output.

(2)Estimate A and B from autoregressive moving average exogenous(ARMAX)model using Bierman U-D update algorithm[21].

(3)The coefficients of polynomials are calculated from the following equations according to the tuning parameters as

(4)The STPID control parameters are found from the values of s0,s1and s2as

(5)The incremental control signal Δu(t)is calculated from the following equation

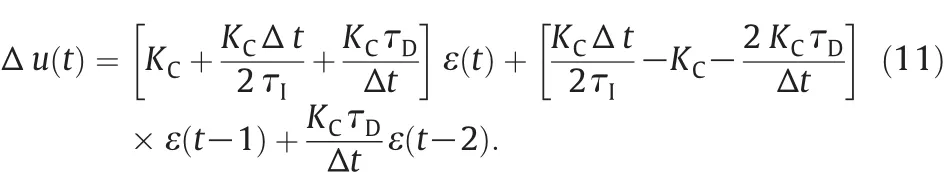
(6)The calculated output value is compared with the set point and thus an error is found.

(7)Return to Step 5.

2.3.Fuzzy control based on fuzzy method with fuzzy identification

One of the fundamental problems faced in the design of fuzzy control systems is the determination of control rules and the establishment of relation matrix.In most cases an operator might not determine and practice suitable control rules.Then the fuzzy model based control is the most widely applied one.The most significant part in building a model based control is the establishment of a model.The simplest model,as we all know,is dependent on the experience of the operator[22].The structure of the fuzzy model based controller is shown in Fig.1.

2.3.1.Fuzzy model identification

Fuzzy relation matrix may be in several different forms.The matrix used in this paper is first degree and has a single input-single output.The model of this form is given below[23].

where∘is the max-min composition;Y and U are the possibility vectors for model output and input,respectively and R is the model relation matrix.Subscribed k represents current time,and k−1 one sampling time in the past and the dead time of d sampling periods in the past.

The fuzzy identification procedure applied is given as follows:

(1)The model form is as given in Eq.(12).

(2)Appropriate sets of fuzzy reference sets for the input and output is selected such as given in the present work(see Figs.9-10 and 12-13).

(3)Appropriate input-output data are collected from the process such as obtained and given in the present work(see Fig.4).

(4)The identification algorithm described below is applied to evaluate the model relation matrix.

2.3.2.Model(the model relation matrix)identification algorithm

(1)Initial relation matrix R is identified.This matrix can either be empty or have some knowledge of the operator or the engineer.

(2)Yk,Yk−1,Uk−dare defined as sets.

(3)The data obtained are fuzzified and turned into Yk,Yk−1,Uk−dvectors.

(4)A relation matrix is formed

(5)Maximum values of the members in vectors Uk−dand Yk−1are defined with i*and j*.

(6)R is updated from R′according to the relation below:

where i*and j*are the positions of the maximum membership values in the possibility vectors Ukand Yk−1,respectively and a is a scalar constant between 0.5 and 1.0.

(7)In case of more data,Step 2 is repeated.

Application of N reference sets for each variable gives N×N×N relation matrix(in the case studied,5 reference sets for each variable are chosen).

3.Experimental Setup and Method

3.1.Reaction of neutralization with weak acid-strong base

In this study,the neutralization reaction of acetic acid with sodium hydroxide is selected.Because of the fact that acetic acid has a balanced reaction with sodiumhydroxide and does not completely separate in its components,the system acts as a buffer solution between pH of 4 and 6.5(Fig.2)[24].In the experimental control cases studied,base flow rate was manipulated to maintain pH value at pH=7.

Fig.1.Fuzzy model based controller.

Fig.2.Titration curve of the neutralization reaction in the solution with 0.01 mol·L−1 acetic acid and 0.01 mol·L−1 sodium hydroxide(K a=1.0 × 10−5).

3.2.Experimental method

All the experiments in this study were performed in a continuously fed tubular flow reactor from which products were obtained(Fig.3).Operating conditions were constructed in such a way to maintain the internal temperature of the reactor and the temperature of the water jacket at 20°C.In order to achieve the required temperature,water jacket was fed with tap water at a certain flow rate and then the flow rate was decreased when the jacket was filled with water.Experimental run was for 4200 s.

Fig.3.Schematic diagram of the experimental system.1—computer;2—acetic acid tank;3—reactor output;4—rotameter;5—triac;6—heater;7—preamplifier(pump);8—preamplifier(thermocouple);9—preamplifier(pH probe);10—agitator;11—thermocouple;12—pH meter;13—peristaltic pump;14—sodium hydroxide tank;15—jacket input;16—jacket output.

The temperature was kept at 20°C(room temperature)by means of the heater in the water jacket controlled by on-off control systems.Then,concentrated solutions of 0.01 mol·L−1NaOH and 0.01 mol·L−1CH COOH were placed in the acid and base tanks feeding the reactor.The temperature of both feeding tanks was set at about T=20°C.Peristaltic pumps fed the solutions prepared at this temperature to the reactor at certain flow rates.First,steady state conditions were determined for pH=7.Process parameters are tabulated in Table 1.

Table 1 Process parameters of the experimental system

Some control experiments were conducted in this study.Base flow rate was chosen as the manipulated variable.First,the system was driven to steady state with the desired pH.Next,pH was tried to be kept at the desired value by applying PID,self tuning PID and fuzzy controllers in the system which deviated from steady state because of load effects and changes given to set point.

Acetic acid,sodium hydroxide acts like a buffer solution between pH of 4 and 6.5.Above 6.5,a fast increase occurs in the pH of the solution and this gives the property of nonlinearity to the system.Since the pH of the reactor is measured at the exit,depending on the flowrates of the solutions used,it has an extremely long time lag(approximately 300 s).This time lag makes it rather difficult to control the system and eliminate the effects of disturbance.

4.Results and Discussion

4.1.Conventional PID control results

Selection of PID control parameters is crucially important in controlling a tubular flow reactor by PID because of the nonlinear characteristic of pH neutralization process.In this study PID parameters were calculated by three different methods and the tubular flow reactor was controlled under similar conditions using these parameters separately.Table 2 lists the methods applied and PID parameters.

Table 2 Comparison of PID control parameters on the basis of the methods

In the first part of the study,acetic acid flow rate was subjected to a negative or a positive step change of 20%and the system was controlled using PID algorithm with the parameters identified by the Cohen-Coon,Jutan-Rodriguez and Yuwana-Seborg methods.Quantitative evaluation of the study with IAE and ISE criterion was illustrated in Table 3.

Table 3 IAE and ISE values by PID control in response to a negative and positive step change in acetic acid flowrate

The control performance is observed when the set point of the system is decreased from pH of 7 to 6.5.Quantitative results of this run are given in Table 4.In the case of a positive step change in the setpoint from pH of 7 to 9,parameters determined by the Jutan-Rodriguez method serves to achieve the best control.When a negative step change is employed in the set point from pH of 7 to 6.5,the best control performance is realized with PID parameters identified by the Cohen-Coon method.

Table 4 IAE and ISE values by PID control in response to a negative and positive step change in set point

4.2.Self tuning PID control results

In this study pH control of a tubular flow reactor was realized by using a self tuning PID algorithm.Effective operation of a self tuning PID system depends on the proper calculation of the parameters of ARMAX model used.Model parameters(a1,a2,b0)were calculated by the Bierman algorithm.PRBS signals were employed in the calculation.These signals were sent to the process experimentally by making step changes in base flow rate and the response of the system was detected by an online computer through pH measurements.The open loop system dynamic behavior in the face of pseudo random binary sequence(PRBS)excitation is shown in Fig.4.

Fig.4.Open-loop system dynamic behavior in the face of PRBS excitation[manipulated variable(base flow rate,ml·min−1)and output response(pH)].

The ARMAX model is given below:

This model was employed for all self tuning PID control studies,but for an efficient control t chosen as the tuning variable must be estimated well.Accordingly some control experiments were conducted and variations were made in t in order to get an efficient control.In this study t2and t were taken as 0.

As in the previous experiments,the tubular flow reactor is set to steady state with an output pH of 7 and self tuning PID controller maintains pH at 7 when a negative step change of 20%is given to the acetic acid flow rate.However,the achievement of an effective control requires tuning of t with different values.Fig.5 illustrates results of such experimental trials.The change in pH with time is observed when different t values are employed.IAE and ISE values for different t values are provided in Table 5 to help make a quantitative analysis.The calculations and results indicate that the best value of t enabling an effective control is0.2.

Fig.5.STPID control with a negative step change of 20%in acetic acid flowrate.

Table 5 IAE and ISE values by STPID control in response to a negative and positive step change in acetic acid flowrate

It can be observed in Fig.6 that when the acetic acid flow rate is subjected to a negative step change of 20%,self tuning PID is able to control the systemat pH of7 after a while at all tuning parameters as in PID control.Quantitative results for different tuning parameters are given in Table 5.As seen in the table,although tuning parameter does not have a significant impact on the control under such conditions,t1=0.06 could be regarded as the best tuning parameter for control.

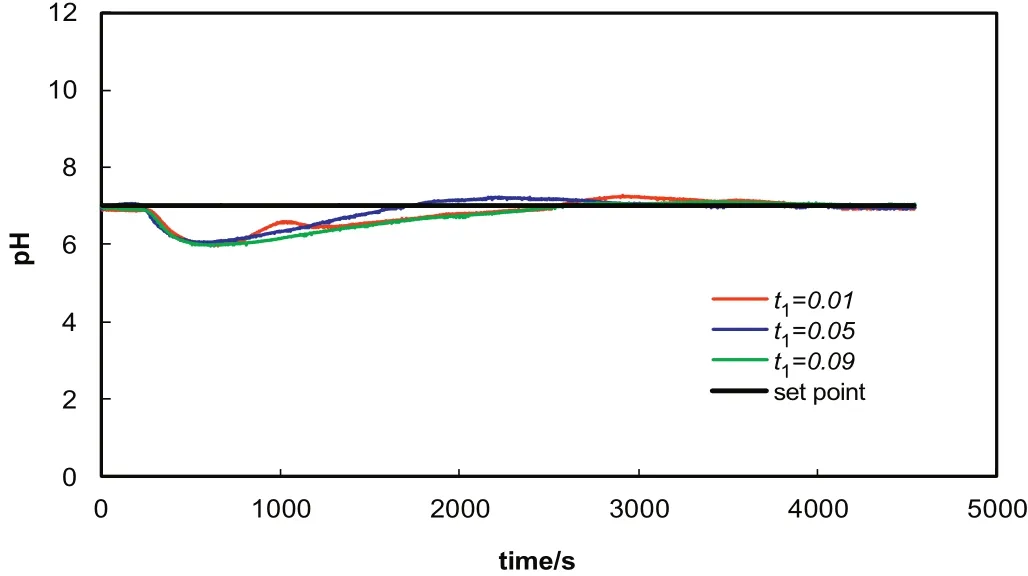
Fig.6.STPID control with a positive step change of 20%in acetic acid flowrate.

Fig.7 demonstrates how self tuning PID system controls the pH in response to a positive step change in set point from pH of 7 to 9.Self tuning PID responds to such a change in the set point and yields a good control for all the parameters after facing some oscillation.The results of this control are given in Table 6 in which the best tuning parameter is obtained with t1=0.09.

Fig.7.STPID control in the face of a positive step change in the set point from pH of 7 to 9.

Table 6 IAE and ISE values by STPID control in response to a negative and positive step change in set point

In all the experimental runs,the other set point change employed is a negative one from pH of 7 to 6.5.A desired satisfactory control of pH is achieved by self tuning PID with a negative set point change.Self tuning PID controller is able to keep the pH at the set point of 6.5 after some oscillation observed in the system.Control results under these conditions are tabulated in Fig.8.There is no doubt that the best control is realized when the tuning parameter is t=0.9(Table 6).

Fig.8.STPID control with a negative step change in the set point from pH of 7 to 6.5.

4.3.Fuzzy control results

This part of the paper investigated the control of pH at the exit of a tubular flow reactor by a fuzzy system.First,membership functions were designed for pH and base flow rate and then the relation matrix was calculated.

In order to enable a fuzzy system to operate efficiently,it is vitally important to identify and calculate the fuzzy membership function well.PRBS signals given in Fig.4 are employed in the calculations.A triangular membership function is preferred and the number of the functions is 5.Right and left widths of the triangular membership function are taken as equal to one another.Fuzzy membership functions constructed for positive and negative step changes of20%in acetic acid flow rate are depicted in Figs.9 and 10.

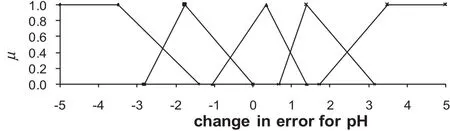
Fig.9.Fuzzy membership function for a change in error for pH(for positive and negative step changes of 20%in acetic acid flowrate).

Fig.10.Fuzzy membership function for a change in error for base flowrate(for positive and negative step changes of 20%in acetic acid flowrate).

As in other control methods, first the process is brought to steady state at pH of 7.Then some load effects are introduced to the system and fuzzy control is applied to keep the pH at 7 against the load effects.

Fuzzy control results in the presence of positive and negative step changes of 20%in acetic acid flowrate are reported in Fig.11.Fuzzy model could control the system with a small oscillation around the set point under both disturbing effects.

Fig.11.Fuzzy control performance in the presence of positive and negative step changes of 20%in acetic acid flowrate.

Fuzzy membership functions identified for the set points of positive and negative effects are given in Figs.12 and 13.pH control by fuzzy system for a given positive step change in the set point from pH of 7 to 9 is given in Fig.14.It is obvious in this figure that fuzzy controller could control the desired setpoint with a suitable oscillation when such a step change is employed in the set point.Another set point change made is from pH of 7 to 6.5.Fuzzy control system could manage to maintain pH at the desired set point of 6.5 with a small oscillation(Fig.14).

Fig.12.Fuzzy membership function for a change in error for pH(for the set points of positive and negative effects).

Fig.13.Fuzzy membership function for a change in error for base flowrate.(for the set points of positive and negative effects).

Fig.14.Fuzzy control results with positive and negative step changes in the set point.

The IAE and ISE values compiled from fuzzy control under various changes in acetic acid flow rate and set point are listed in Table 7.

Table 7 IAE and ISE values compiled from fuzzy control under various changes in acetic acid flowrate and set point

4.4.Comparison of all control results

In all control cases studied,the process was initially driven to steady state at pH of 7.Three different control strategies of PID,self tuning PID and fuzzy control were applied to control the pH at the exit of a tubular flow reactor.The same load effects and the set point changes were employed in these control cases studied.

First of all,PID was tested.PID parameters were determined by different methods of Cohen-Coon,Jutan-Rodriguez and Yuwana-Seborg.Comparison was based on the method that enabled the best control for a given load effect or set point change.Next,self tuning PID was tried out.Different tuning parameters were employed in this control.Comparison was based on the tuning parameter which enabled the best control for a given load effector set point change.Finally,fuzzy control was applied.

Fuzzy system was able to control the reactor after a small oscillation around the set point(pH=7)when a negative step change of 20%was given to acetic acid flow rate,while PID identified by Yuwana-Seborg method could control the system after a bigger oscillation.Self tuning PID was far from controlling the system even with the best tuning parameter of t=0.003.

When a positive step change of 20%was given to acetic acid flow rate,fuzzy control yielded the same control performance as the one conducted with Cohen-Coon based PID parameters,while self tuning PID using the best tuning parameter resulted in worse result than others.

When a positive step change was made in the setpoint from pH of 7 to 9,PID identified by the Jutan-Rodriguez method and self tuning PIDcould control the system at the desired set point with a small oscillation.Fuzzy control,on the other hand,faced oscillations around set point.Self tuning PID achieved the best control with the tuning parameter of t=0.009.

When a negative step change was made in the setpoint from pH of 7 to 6.5,PID identified by Cohen-Coon could control the pH at the desired set point without any oscillation.Self tuning PID maintained the set point pH at 6.5 with a small oscillation.Fuzzy algorithm controlled the system at the set point with oscillation.

The performance of fuzzy control system depended on fuzzy membership functions and relation matrix.Thus,it could be an effective controller over a wide range of conditions if relation matrix and fuzzy membership functions could be adjusted for the conditions given.Depending upon the response the rules that will govern all possible situations can be designed.

5.Conclusions

Experimental pH control in the nonlinear region was achieved successfully in tubular flow reactor with the existence of high dead-time by using three different control strategies of conventional PID,self tuning PID and fuzzy algorithms,respectively.By comparing the application performance of conventional and self-tuning PID algorithms,it is found that the conventional PID control technique with nonparametric system identification method showed better results than self-tuning PID control with parametric identification method in the experimental cases studied.Conventional PID technique has been highly applied in industry.Thus,this method was used as base for experimental control application performance comparison.The success of experimental fuzzy control application based on fuzzy model has been shown clearly by comparing the values of performance criteria obtained with the results of conventional PID application.

In the current study acetic acid sodium hydroxide neutralization reaction was carried out in a tubular flow reactor.In the acetic acid sodium hydroxide neutralization process,the solution acted as a buffer solution from pH of 4 to 6.5.Within the range of pH of 6.5 to 8.5 a sudden increase was observed and from pH of 8.5 to 12 the solution turned back to its buffer solution nature.In ideal wastewater treatment,water discharged into the environment must contain no chemicals(all of them must be removed from wastewater),no base or acid and it must be at pH=7.As the titration curve suggests,it was not easy to keep pH at 7 in acetic acid sodium hydroxide reaction.In addition,there was a great lag time since the pH was measured at the exit of the reactor.This created extra burden on the pH control.Three different control strategies employed in control studies are PID,self tuning PID and fuzzy control.The efficiency of these methods was evaluated with the IAE and ISE criteria.As a conclusion fuzzy control was better at controlling pH in the tubular flow reactor than the other two methods PID and self tuning PID.The result of experimental works stated that the performance of PID and fuzzy controllers was satisfactory.Based on these experimental results,fuzzy controller can be very effective and it was promising for pH control in a highly nonlinear process operated over a wide range of conditions.

Nomenclature

aiparameters of A polynomial

biparameters of B polynomial

Caacid concentration,mol·L−1

Cbbase concentration,mol·L−1

CHhydrogen ion concentration,mol·L−1

Kaacidity equilibrium constant(=1.8×10−5)

Kcsteady-state gain for controller

Kwdissociation constant of water(=1×10−14)

qaacid flowrate,ml·min−1

qbbase flowrate,ml·min−1

R model relation matrix

r(t) set-point at time t

t1tuning parameter

U possibility vector for model input

u(t) input variable at time t

Y possibility vector for model output

y(t) output variable at time t

z,z−1forward and backward shift operators

(t) difference between the measured variable and set point at time t

τDderivative time,min

τIintegral time,min