Lattice Boltzmann simulation of double diffusive natural convection in a square cavity with a hot square obstacle

Mohsen Nazari*,Ladan Louhghalam,Mohamad Hassan Kayhani

Department of Mechanical Engineering,University of Shahrood,Shahrood,Iran

Keywords:Lattice Boltzmann method Double diffusion Hot obstacle Opposing buoyancy force

ABSTRACT Double diffusion convection in a cavity with a hot square obstacle inside is simulated using the lattice Boltzmann method.The results are presented for the Rayleigh numbers 104,105 and 106,the Lewis numbers 0.1,2 and 10 and aspectratio A(obstacle height/cavity height)of0.2,0.4 and 0.6 for a range of buoyancy number N=0 to−4 with the effect of opposing flow.The results indicate that for|N|＜1,the Nusselt and Sherwood numbers decrease as buoyancy ratio increases,while for|N|＞1,they increase with|N|.As the Lewis number increases,higher buoyancy ratio is required to overcome the thermal effects and the minimum value of the Nusselt and Sherwood numbers occur at higher buoyancy ratios.The increase in the Rayleigh or Lewis number results in the formation of the multi-cell flow in the enclosure and the vortices will vanish as|N|increases.

1.Introduction

Natural convection occurs because of the buoyancy effect due to temperature gradient.There are also gradients of other scalar quantities such as species concentration in a flow.The flow driven by the joint effect of temperature and species concentration gradients is called double diffusive natural convection(DDNC),which appears in many fields such as astrophysics,oceanography,geology,biology,chemistry and limnology[1],and has many engineering applications such as in crystal growth,energy storage,chemical processes[2].

Natural convection in enclosures has been studied comprehensively[3-5].Moreover,double diffusive convection has been the subject of study for many researchers[6,7].DDNC of a non-Newtonian fluid in a shallow horizontal cavity was studied analytically and numerically where the short walls were submitted to uniform heat and salt fluxes and horizontal walls were insulated and impermeable[2].Double diffusion convection coupled with radiation was numerically studied in a square cavity[8].In their study the finite volume method was utilized by implementation of a SIMPLER algorithm for coupling of velocity and pressure,and to model radiation heat transfer equation,the discrete ordinate method was used.Nikbakhti and Rahimi[9]numerically studied DDNC in a rectangular cavity.In their study,a part of vertical walls with their length half their cavity height was considered at a constant temperature and concentration.The active part of the left wall had a greater temperature and concentration than the active part of right wall while horizontal walls,and inactive parts of vertical walls had no diffusion.Since placement order of active zones plays a huge role in heat and mass transfer,they considered nine different positions for active parts.For the nine positions the active zones were at the top,middle and bottom.

Recently the Lattice Boltzmann method has successfully substituted the conventional methods such as finite volume method and finite element method.The privilege of this method is its capability in calculating complex geometries,complex boundaries and multiphase flows.Many researchers have studied fluid flow and heat transfer in enclosures and micro-channels using the Lattice Boltzmann method[10-17].Among them,some authors studied double diffusive natural convection using LBM.Ma[18]proposed a temperature-concentration lattice BGK model to simulate DDNC in a rectangular cavity in the presence of a magnetic field and heat source.In the rectangular cavity,horizontal walls were insulated while vertical walls were set to constant temperature and concentration.A uniform magnetic field was applied in the x direction.DDNC in an open cavity was studied using lattice Boltzmann method[19].A simple D2Q9 model was used for flow while for temperature and concentration a D2Q4 model was applied.The square cavity has insulated and impermeable horizontal walls while the vertical walls have constant temperature and concentration.In this study only the opposing buoyancy forces were investigated.

While LBM simulation of DDNC was previously investigated by many researchers,to the best knowledge of the authors DDNC in the presence of an obstacle is not yet addressed in the literature.The species concentration induced buoyancy force either aids or opposes the thermally driven flow,determined by the value of the buoyancy ratio,i.e.the ratio of the concentration buoyancy force to the thermal buoyancy force.In this paper we investigate double diffusive natural convection in a square cavity in the presence of a hot square obstacle.The effect of aiding flow(N＞0)is not the subject of interest.

2.Method of Solution

A simple D2Q9 scheme is applied for flow,temperature and concentration.Fig.1 shows geometry of the problem and the boundary conditions.North and south walls are adiabatic(no temperature or concentration diffusion),while left and right boundaries have constant temperature and concentration.All walls of the obstacle have unit temperature and concentration.The Prandtl number is 0.71.

Fig.1.Cavity geometry and boundary conditions.

Streaming and collision terms of flow are presented as[20]:

where fa(x+eaΔt,t+ Δt)is the streaming part and the right hand side of the equation is the collision term.is the equilibrium distribution function and τ is the relaxation time.The equilibrium distribution functionis given by

whereρand u are the density and microscopic velocity respectively and ωais the weight factor which are defined for the D2Q9 model as

The velocities eaare[19]

where c= Δx/Δt,Δx is the lattice space and Δt is the lattice time step size which is set to one.

In Eq.(1),Fais the force term in each direction and can be defined as[20]:

where F is

In the above,gr,βTand βCare gravity acceleration,thermal expansion coefficient and concentration expansion coefficient and ΔT and ΔC are temperature and concentration differences respectively.The buoyancy ratio(N)is defined as

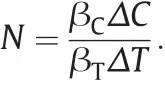
The macroscopic velocity u and density ρ can be obtained through the first and zeroth moment of the particle distribution f,i.e.[20-22]:

The kinematic viscosity in the D2Q9 method is defined as[20-22]:

Temperature(or concentration)streaming and collision are presented in this manner[19]:

where Φ(x,t)is either the temperature or the concentration.For D2Q9 model ωsis given by

where Γ is the diffusion coefficient for temperature(α)or concentration(D).The temperature and concentration can then be calculated at any point in the domain:

The average Nusselt number is defined as

where ΔX is the dimensionless lattice spacing.The average Sherwood number can be calculated in a similar manner:

where M is the number of lattice nodes in Y direction.After the streaming process the distribution functions in the domain are obtained.The distribution functions toward the domain,which are unknown,are then determined by applying the boundary conditions.

2.1.Boundary conditions

2.1.1.For flow

On-grid bounce back boundary condition is applied on the cavity and obstacle boundaries.

2.1.2.For temperature(or concentration)

For insulated(impermeable)walls,bounce back boundary condition is used.Knowing the wall temperature(or concentration),unknown distribution functions on vertical walls of the cavity and obstacle walls are determined.For instance on the right side of the obstacle(Th=1):

where i is the location of the right side of obstacle in X direction.

3.Results and Discussion

3.1.Validation of the method

In order to validate the present numerical method,the results of LBM are validated by the data reported by Beghein et al.[23]in a simple square cavity.They studied steady-state thermo-solutal convection in a square cavity filled with air,subjected to horizontal temperature and concentration gradients,numerically.This comparison is shown in Fig.2(a)where the local Nusselt number is illustrated for Le=1,Pr=0.71,RaT=RaC=104.

It is assumed herein that when the average Nusselt number reaches a constant value,the results are convergent.This is illustrated for Ra=105,Le=2 and A=0.4 in Fig.2(b).

The average Nusselt number along the vertical axis is also calculated and compared with the results of Beghein et al.[23]for different buoyancy ratios(see Table 1).It can be seen that the results predicted by the LBM model are in good agreement with the results of Beghein et al.[23].For the numerical simulations,120×120 lattices are used for Ra=104,150×150 lattices are employed for Ra=105,and 200×200 lattices are considered for Ra=106.We further refine the grid with 400×400 lattices,but no obvious improvement is observed.The values of the local Nusselt numbers at the left wall of the cavity are plotted against the number of grids and the results showed that the obtained numerical results are independent of the number of nodes.We have also checked all the important parameters(such as N,Le,A and Ra.)to obtain correct number of lattices.For double dispersion flow,the magnitude of the velocity should be of the order ofwhere M is thenumber of lattices.By definition of Ra and Pr numbers,the characteristic

3.2.The effect of controlling parameters on the flow patterns

Figs.3-6 illustrate the effect of controlling parameters on the flow patterns.When N=0,the driving force is the buoyancy force induced only by the temperature gradient.As|N|increases(more negative),the effect of concentration gradient will be added to the force term.However,when|N|＜1, flow is influenced by the buoyancy force due to temperature gradient.Once|N|＞1,the concentration buoyancy effect increases and the direction of flow patterns would change.

Fig.3 shows the streamlines in case of Ra=104,Le=0.1.As it can be observed the flow inside the cavity forms a double-cell flow.Here,the Lewis number is not very high(Le≪10)so the temperature diffusion compared to the concentration diffusion is not very effective.In contrary,when Le=10(Fig.4)the effect of temperature diffusion is high compared to that of concentration.Therefore,although the Rayleigh number is not very high(Ra=104),the temperature diffusion will affect the flow patterns and multi-cell flow patterns are witnessed in|N|＞1.The reason is that when Le is high(Le=10),the temperature diffusion is higher compared to concentration diffusion.Thus,for concentration buoyancy to dominate temperature buoyancy,higher N is required.When buoyancy ratio is near unity,the effect of temperature is not completely dominated by concentration effect due to the higher Lewis number and some parts of the flow will form small vortices which are moving in the opposite direction in respect to the direction of the main flow.As|N|increases,these vortices will shrink in size and join the main flow.

Fig.5 illustrates the flow pattern in the case of Ra=105,Le=0.1.As it can be seen,the flow inside the cavity is in the form of double-cell.By increasing the Rayleigh number to 106,the effect of temperature increases and in case of Le=2(Fig.6),although the Lewis number is not very high(Le≪10),multi-cell flow pattern is observed in the cavity due to the increase in the temperature effect.

Fig.2.(a)Local Nusselt number along the vertical wall of the cavity for Le=1,Pr=0.71,Ra T=Ra C=104.(b)Average Nusselt number per number of iterations for different buoyancy ratios in case of Ra=105,Le=2,A=0.4.

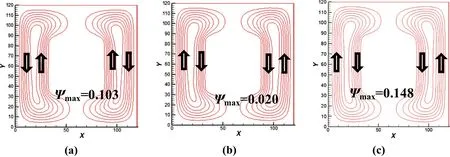
Fig.3.Streamlines in case of Ra=104,Le=0.1,A=0.4 and(a)N=0.0,(b)N=−1.2,(c)N=−2.5.

Fig.4.Streamlines in case of Ra=104,Le=10,A=0.4 and(a)N=−1.2,(b)N=−1.5,(c)N=−2.5.

3.3.Rayleigh number

Figs.7 and 8 show the effect of Rayleigh on the isotherms and isoconcentrations.When Ra=104,isotherms are almost vertical.This indicates the dominance of conduction heat transfer in the cavity.As the Rayleigh number increases at a constant buoyancy ratio,the convection heat transfer will become dominant and isotherms bend toward the cavity and obstacle boundaries.It was also observed that the form of isotherms changes with the variation of N.The results showed that with the increase in|N|,the effect of concentration increases.However,at N=−0.8,the thermal buoyancy was still dominated in the enclosure and the isotherms were similar to the case of N=0.

Fig.5.Streamlines in case of Ra=105,Le=0.1,A=0.4 and(a)N=−0.8,(b)N=−1.2,(c)N=−2.5.

Fig.6.Streamlines in case of Ra=106,Le=2,A=0.4 and(a)N=−0.8,(b)N=−1.2,(c)N=−1.5,(d)N=−2.0.

When N=−1.2,the concentration buoyancy would overcome the effect of thermal buoyancy and the isotherms curvature would be in the reverse direction compared to the case of|N|＜1.It should be noted that as the Rayleigh number increases,due to the increase of thermal effect,the domination of solute buoyancy to thermal buoyancy force and thereby the diversion of isotherms curvature would occur at higher buoyancy ratios.It was observed that as the Rayleigh number increases,the curvature of iso-concentrations increases and the isotherms will be denser near the boundaries.With an increase in the buoyancy ratio to more than one,the curvature direction of isoconcentrations reverses.

The effect of Rayleigh number on the variation of the average Nusselt number on the left wall of enclosure with buoyancy ratio is illustrated in Fig.9.One can see that the Nusselt number and thereby the heat transfer rate increase with the Rayleigh number.As it can be observed in all the Rayleigh numbers as|N|increases,the Nusselt number decreases to a minimum value,then it starts to increase again.This trend is expected because when|N|＜1,the net force(Eq.(6))decreases with the increase of|N|.When buoyancy ratio is greater than N=−1,the average Nusselt number increases with|N|due to the increase in the net force.The reason that the minimum value of the Nusselt number doesn't occur at N=−1 exactly is that the Lewis number is not equal to one so the thermal boundary layer thickness is not equal to that of the concentration boundary layer[19].

Fig.7.The effect of Rayleigh number on the isotherms in case of Le=2 and A=0.4 and N=-1.2.

Fig.8.The effect of Rayleigh number on the iso-concentrations in case of Le=2 and A=0.4 and N=-1.2.

Fig.10 shows the effect of the Rayleigh number on the variation of the Sherwood number with buoyancy ratio for Le=2 and A=0.4.It is observed that the average Sherwood number on the left wall of the enclosure,which represents the mass transfer rate,increases with the increase of the buoyancy ratio.Here the same pattern as the Nusselt number is observed and the Sherwood number decreases with|N|and then starts to increase for|N|greater than 1.The reason is that the net force decreases with N when|N|＜1 and increases with the buoyancy ratio for|N|＞1.One can also see here that the minimum value of the Sherwood number doesn't occur at N=−1 exactly due to the fact that the Lewis number is not equal to unity.

3.4.Lewis number effects

The effect of the Lewis number on the isotherms is illustrated in Fig.11 for Ra=105and N=-1.2.The results were also studied for other buoyancy ratios.It was observed that when N=−0.8,the thermal effects dominated the concentration effects,and as the Lewis number increased,these effects were increased.On the other hand,when|N|＞1,thermal effect would decrease compared to that of concentration and the curvature direction of the isotherms would change.However,the effect of heat conduction increases with the Lewis number.As it can be seen,for N=−1.2 when the effect of concentration is justs lightly more than the thermal effect(|N|≪4),as the Lewis number and thereby the thermal diffusion effect increase,the concentration effect is reduced to some extent that its overcoming to the thermal effect is not clear.However,in the case of N=−4,where the solute effect was significantly more than the thermal effect,the concentration effect was seen to still be dominated as the Lewis number increases to Le=2 and the density of isotherms near the north boundary of obstacle was slightly less than the case of Le=0.1.

Fig.9.The effect of Rayleigh number on the variation of Nusselt number with buoyancy ratio in case of Le=2 and A=0.4.

Fig.12 shows the effect of the Lewis number on the iso-concentrations.The effect of the buoyancy ratio on iso-concentration was also studied.The results showed that when|N|＜1,the curvature of isoconcentrations increases with the Lewis number,while when N=−1.2,the curvature of iso-concentrations decreases with the increase of the Lewis number.For large N such as N=−4,the curvature increases with the Lewis number.The reason is that when N=−1.2,the solute effect is slightly more than the thermal effect and increase of the Lewis number to 20 times higher will overcome this effect.On the other hand when N=−4,the effect of concentration is much higher than that of temperature and increase in the Lewis number and thereby thermal diffusion can't dominate this effect.

Figs.13 and 14 illustrate the effect of the Lewis number on the variation of the average Nusselt number with buoyancy ratio for Ra=104and Ra=105respectively.When N=0 it is only the temperature gradient that influences the flow and therefore in all the Lewis numbers,the Nusselt numbers corresponding to this case are the same.One can see that as the Lewis number increases,the minimum value of the Nusselt number shifts toward the higher buoyancy ratios due to the fact that the concentration boundary layer thickness decreases with increase in the Lewis number compared to the thermal boundary layer thickness.Thus the effect of solute buoyancy decreases and higher buoyancy ratios are required to overcome the decrease in concentration buoyancy effect.

Fig.10.The effect of Rayleigh number on the variation ofSherwood number with buoyancy ratio in case of Le=2 and A=0.4.

Fig.11.The effect of Lewis number on the isotherms in case of Ra=105 and A=0.4 and N=−1.2.

Fig.12.The effect of Lewis number on the iso-concentrations in case of Ra=105 and A=0.4 and N=−1.2.

The effect of the Lewis number on the variation of the Sherwood number is illustrated in Figs.15 and 16 for Ra=104and Ra=105respectively.As a general trend,the Sherwood number first decreases with N and then increases.Also it can be seen that for N=0,the Sherwood number increases with the Lewis number due to the decrease of concentration boundary layer thickness compared to that of thermal boundary layer.Thus,the mass transfer rate increases with the Lewis number.

3.5.Aspect ratio effects

Fig.13.The effect of Lewis number on the variation of Nusselt number with buoyancy ratio in case of Ra=104 and A=0.4.

Fig.17 shows the effect of the aspectratio on the isotherms for Ra=105and Le=2.As the aspect ratio increases,the heat transfer area and thereby heat transfer rate increases.One can see that the curvature of isotherms decreases with increase in the aspect ratio.Also,it was observed that the isotherm contours are considerably changed when|N|reaches more than unity.

The same result was observed for iso-concentration.The results showed that with the increase in the aspect ratio,the curvature of isoconcentrations and solute boundary layer thickness decreases while the mass transfer area and therefore the mass transfer rate increase.

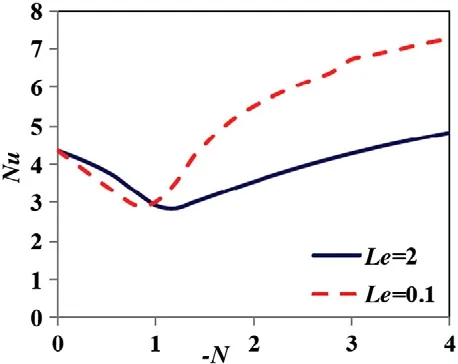
Fig.14.The effect of Lewis number on the variation of Nusselt number with buoyancy ratio in case of Ra=105 and A=0.4.

Fig.15.The effect of Lewis number on the variation of Sherwood number with buoyancy ratio in case of Ra=104 and A=0.4.

Fig.16.The effect of Lewis number on the variation of Sherwood number with buoyancy ratio in case of Ra=105 and A=0.4.

The effect of the aspect ratio on the heat and mass transfer rate is illustrated in Figs.18 and 19 in the form of variation of the Nusselt and Sherwood numbers respectively for Ra=105and Le=2.Both the Nusselt and Sherwood numbers increase with the aspect ratio.This result is expected since the heat and mass transfer area increases with the aspect ratio,thus heat and mass transfer rate increases.Also it can be observed that for|N|＜1,the Nusselt and Sherwood numbers decrease as N increases due to the reduction of net force.Once|N|＞1,the netforce and thereby heat and mass transfer rate increases with|N|.

4.Conclusions

Fig.17.The effect of aspect ratio on the isotherms in case of Ra=105 and A=0.4 and N=−1.2.

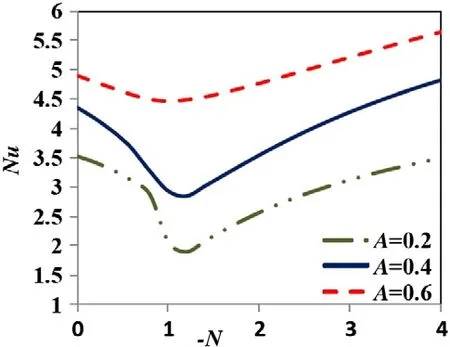
Fig.18.The effect of aspectratio on the variation of Nusselt number with buoyancy ratio in case of Ra=105 and Le=2.

Fig.19.The effect of aspect ratio on the variation of Sherwood number with buoyancy ratio in case of Ra=105 and Le=2.

Double diffusion natural convection in a square enclosure in the presence of a hot square obstacle is studied numerically using LBM.The species concentration induced buoyancy force either aids or opposes the thermally driven flow,which is determined by the value of buoyancy ratio N(positive or negative,respectively).In this study,the effect of opposing flow(N＜0)is the subject of interest.The results show that the Nusselt and Sherwood numbers increase with the increase of the Rayleigh number and aspect ratio.Also,the Sherwood number increases with the Lewis number.The Nusselt and Sherwood numbers decrease with buoyancy ratio to a minimum value and then start to increase for|N|＞1.As the Rayleigh and Lewis numbers increase,more negative N is needed for vortices to join the main flow and the multi-cell flow converts to double-cell flow.

Nomenclature

A aspect ratio

C non-dimensional concentration

c lattice streaming speed,m·s−1

cssound velocity,m·s−1

D concentration diffusion coefficient,m2·s−1

eadiscrete velocity in each direction,m·s−1

F force term of natural convection

Faforce term added to the collision term

fadistribution function

faeqequilibrium distribution function

gathermal distribution function

gaeqthermal equilibrium distribution function

grgravity acceleration,m·s−2

H height of cavity,m

Le Lewis number(α/D)

M number of lattice nodes on the vertical side wall

N buoyancy ratio

Nu average Nusselt number,Eq.(14)

Pr Prandtl number(υ/α)

Ra Rayleigh number(=gβΔTL3/υα)

Sh average Sherwood number,Eq.(15)

T non-dimensional temperature

t time,s

Δt lattice time step size,s

u macroscopic velocity,m·s−1

x lattice coordinate,m

Δx lattice space,m

α thermal diffusion coefficient,m2·s−1

βCconcentration expansion coefficient

βTthermal expansion coefficient,K−1

υ kinematic viscosity,m2·s−1

ρ macroscopic density,kg·m−3

τ relaxation time

ωaweight factor

ωsthermal relaxation time

Subscripts

c cold(concentration or temperature=0)

h hot(concentration or temperature=1)