基于可变权值的动态最短路径算法∗

汪晓洁，汤建国，李娟

(新疆财经大学计算机科学与工程学院，新疆乌鲁木齐830012)

0 引言

现今的网络对信息的交换速度有着很高的要求，在路由区域（routing area）不断变大的情况下，它需要路由更新的速度变得更快.基于链路状态的路由协议在网络中使用非常广泛，例如，Open Shortest Path First[1]（OSPF）和Intermediate System-to-Intermediate System[2]（IS-IS），运行链路状态路由协议的路由器以自己为根节点根据网络拓扑计算一棵最短路径树，并利用该最短路径树计算路由.因此，当网络拓扑结构发生改变时最短路径树的更新效率将直接影响路由的更新速度.

当网络拓扑变化时，需要重新计算SPT.根据静态Dijkstra[3]算法，当网络拓扑变化相对于整个网络的拓扑数量较小时，变化拓扑对已有的SPT影响较小.如果几条链路的改变就导致重新计算整个最短路径树，进而更新路由表，则会导致大量不必要的重复计算，使静态Dijkstra算法变得效率很低.因此，动态更新SPT可以降低计算的复杂性减少冗余的更新，这对网络性能的提高具有重要意义.

动态最短路径更新算法可以分为半动态最短路径算法和全动态最短路径算法[4].半动态最短路径算法或者处理边权值变大，或者处理边权值减校 全动态最短路径算法则对边权值变大或变小均能处理.本文则关注全动态最短路径算法.

1 相关工作

目前，人们在这方面已经做了大量的研究，为了降低计算时间[5]，提出了一种权重变化图G*，它利用有向边和变化节点的位置生成，G∗为网络拓扑的子图，通过G∗可以限制更新节点和链路的范围，从而达到减少冗余更新的目的[6].提出了处理网络拓扑图中边权值减小的MaxR、MinD算法，相比较[4]算法，MaxR和MinD算法具有更高的效率.[5，6]这些算法在一定程度上都可以减少SPT的计算时间，但它们都存在冗余计算的问题.[7]提出了路径节点驱动的思想，并提出了基于路径节点驱动的LCSPT算法.[8]说明了网络是依赖于时间变化的、动态的，证明了动态网络的最短路径问题为NP难，并在此基础上提出了基于稳定区间的近似算法.[9]从遗传算法的角度考虑更新SPT.[10]研究了动态多节点的删除对最短路径更新的影响，提出了MRDA-SPT算法.[11]提出了一种基于脉冲耦合神经网络的模型M-PCNNs来解决最短路径问题.

[12]提出的动态更新DUSPT算法只关注部分的节点和链路，他将节点的更新范围局限在权值变化的终节点的子孙节点和以这些子孙节点为源节点的节点上，此算法不需要对所有的节点和链路重新计算SPT，减少了计算时间，但此算法并未考虑权值变化时，变化链路在拓扑中的位置，节点的更新范围会变大，增加的迭代更新会造成大量的冗余计算.

本文通过深入分析，进一步改善了动态更新SPT的算法，提出了全动态更新IDEWSPT算法，该算法可同时针对权值增大和减小进行处理，不仅可以有效减少计算复杂度还可以减少大量的冗余计算.通过仿真实验验证了本算法的正确性、有效性，并具有更好的性能.

2 IDEWSPT算法

下面给出相关符号和定义，以及IDEW-SPT算法的描述，最后给出IDEW-SPT算法的复杂度分析.

2.1 术语定义

为了方便描述，引入以下符号：

（1）定义网络拓扑图G=(V，E，W)，其中V是网络中节点的集合，E是网络中链路的集合，W是拓扑图中链路的权重，并规定拓扑图中不含负权边；

（2）W(e)代表链路e的权重，且e∈E，表示链路e更新后的权重；

（3）D(i)为节点i在SPT中的最短路径值，它代表从根节点到节点i的所有链路权重的相加和；

（4）Sou-outend(N)={e|S(e)∈N，E(e)/∈N}；

（5）End-outsou(N)={e|S(e)/∈N，E(e)∈N}.

定义1对于有向链路e：i→j；

（1）i称为链路e的源节点，记为S(e)；

（2）j称为链路e的终节点，记为E(e)；

（3）若e∈SPT，且i是e的源节点，j是e的终节点，则节点i称为j的父节点，记为P(j)，即P(j)=i.

定义2节点i的子孙节点是从节点i通过SPT中的边可达的所有节点的集合，且包括i节点本身，记为sub(i).

2.2 算法描述

为了减少计算时间，SPT的计算过程根据链路的变化分为两大部分，链路权重增大和权重减小.SPT中某条链路e的权重变大时，只有集合sub(E(e))的节点和这些节点相关的链路才可能发生变化，其他的节点和链路不会发生任何变化.IDEW-SPT算法只考虑这些节点和链路.当SPT中某条链路e的权重减小时，集合sub(E(e))中的节点的最短路径值减少d=w(e)−w(e)，如果节点的最短路径值发生改变，则重新选择的最短路径一定会经过e.

在IDEW-SPT算法中，N为节点集合，包含所有需要更新的节点，每个N中的节点有一个M.v.inc属性，代表v节点的所有入边中权重的最小增量值.L为链路集合，存储所有变化的链路，每个元素e有一个min-inc属性，代表节点E(e)最短路径的增加值，且可为负值.当有链路需要加入集合L时，执行入队操作L（e，min-inc），出队操作Sel-min（L）将选择L中min-inc最小的链路，并将该链路从L中移除.

假设网络拓扑G=(V，E，W)，根据此拓扑图使用静态Dijkstra算法构造SPT.

有一条链路e：i→j的权重从w(e)变为

If，and eSPT，

d，执行权值增大，End If；

Ife∈SPT，执行权值减小-1；else执行权值减小-2，End If；

End If

权值增大

将j加入N，N.j.inc=d，L(e，d)；

for∀v∈sub(j)，按N中节点的D(v)值依次选择v；

选择链路e，E(e)=v，S(e)/∈sub(j)，and minimum{w(e)}//即e是所有以E(e)为终节点，S(e)为源节点的链路中权重最小的一条链路；

min-inc=D(S(e))+w(e)−D(E(e))，

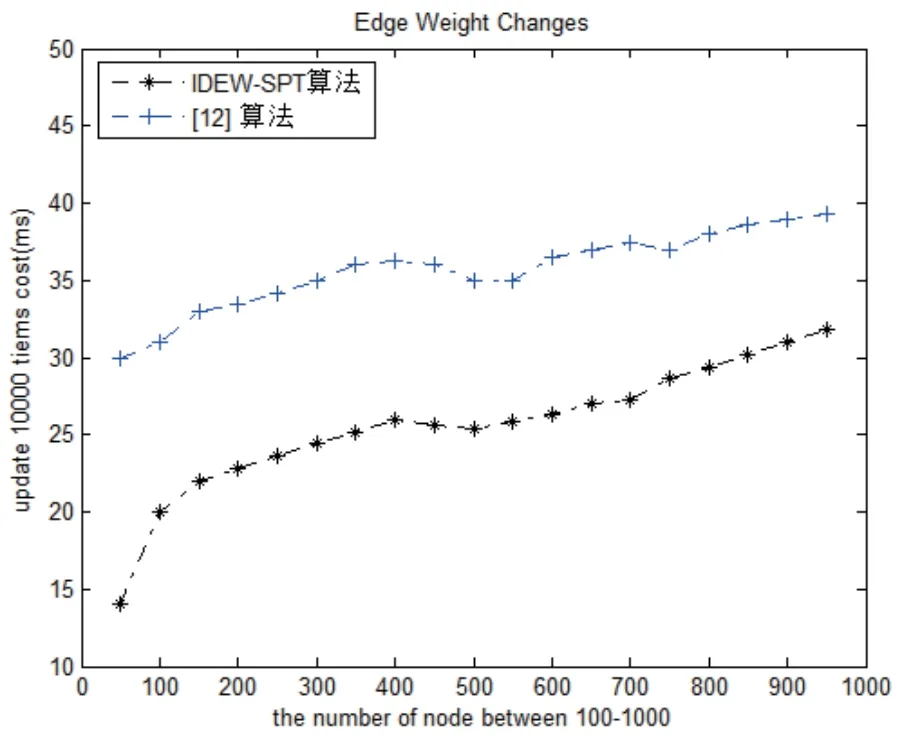
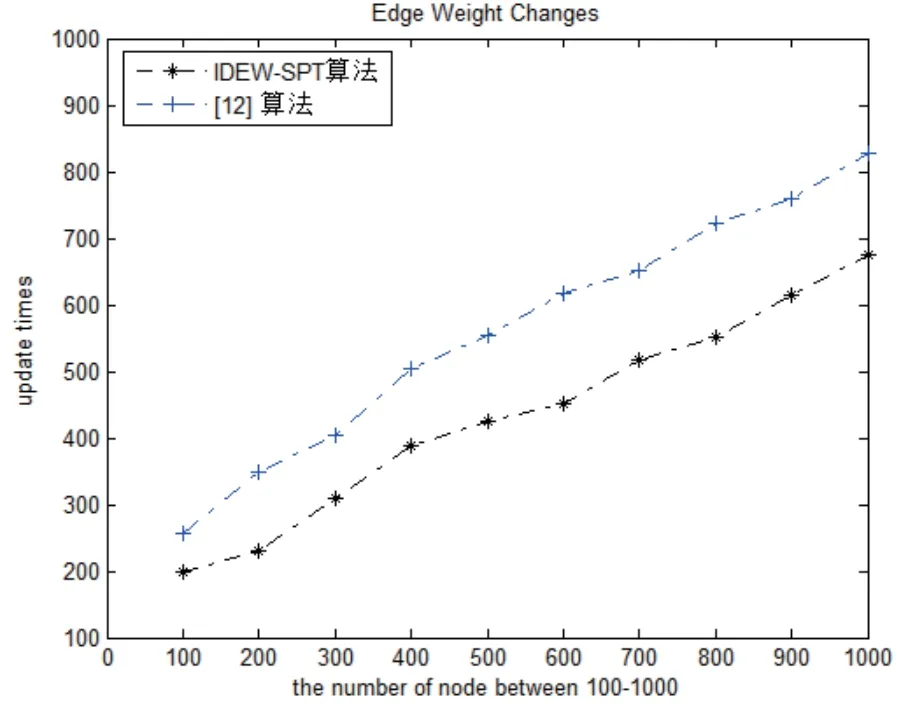
If min-inc

L(e，min-inc)，N.v.inc=min-inc，End If；

chi是v在SPT中的直接相连的子节点，∀chi，将chi加入N，N.chi.inc=N.v.inc；

End For；

whileL∅；

Sel-min(L)→{e1，min-inc}，P(E(e1))=S(e1)；

∀v∈sub(E(e1))andv∈N，D(v)=D(v)+min-inc；

从L中移除终节点为sub(E(e1))的链路，从N中移除Sub(E(e1))；

∀e∈Sor-outend{sub(E(e1))}ande∈End-outsor{N}，

min-inc=D(S(e))+w(e)−D(E(e))；

If min-inc

N.E(e).inc=min-inc，L(e，min-inc)，End If；

End While，执行步骤1；

权值减小-1

∀v∈sub(j)，D(v)=D(v)+d；

for∀e，S(e)∈sub(j)，∀E(e)选择w(e)的值最小的边；

min-inc=D(S(e))+w(e)−D(E(e))；

If min-inc<0，

D(E(e))=D(S(e))+w(e)，P(E(e))=S(e)，min-inc=D(v)−D(E(e))，End If；∀v∈(sub(E(e))-E(e))，IfD(v)-min-inc≤D(v)，

D(v)=D(v)-min-inc，End If；

End For

执行步骤1；

权值减小-2

∀v∈sub(j)，D(v)=D(v)+d；

∀e，S(e)∈sub(j)，∀E(e)选择w(e)的值最小的边；

min-inc=D(S(e))+w(e)−D(E(e))；

If min-inc<0，

L(e，min-inc)，End If；

While

Sel-min(L)→{e1，min-inc}，P(E(e1))=S(e1)；

∀v∈sub(E(e1))，IfD(v)＋min-inc≤D(v)，

D(v)=D(v)＋min-inc，End If；

从L中移除终节点为sub(E(e1))的链路；

∀e∈Sor-outend(sub(E(e1)))，∀E(e)选择w(e)的值最小的边；

min-inc=D(S(e))+w(e)−D(E(e))，

If min-inc<0，L(e，min-inc)，End If；

End while，执行步骤1；

3 算法复杂度分析

假设有一个边的权重发生变化，Q表示最短路径要变化的节点的集合，Tp是Q中节点的数目，参数Q和Tp只依赖网络的拓扑结构和初始SPT.Dmax表示和一个更新节点相连的链路数目的最大值.

算法复杂度为O(T2p+T2p Dmax).考虑当链路的权重变大的情况，执行一次Sel-min()将花费O(Tp)的时间用于线性数组的查找，并且有Tp次这样的迭代.一个父节点更新时，有|sub(v)|次子节点的更新，|sub(v)|≤Tp，父节点更新的迭代次数不超过Tp，则有.假设一条链路的更新需要花费O(1)的时间，则所有和更新节点关联的链路更新需要O(T2p Dmax).所以算法运行的总时间为O

4 仿真实验

本节采用文献[11]仿真模型来验证IDEW-SPT算法的正确性和有效性.随机产生网络拓扑图，所有节点随机分布在500*500的平面区域内，任意节点间存在边的概率由下式(1)确定:

其中d是节点间的欧几里得距离，如果任意两点间距离在l以内，则它们之间存在连接的概率为k，否则，根据节点间的距离它们之间存在连接的可能性会呈指数性下降.每条边的权重取值范围为1∼100.l定义为：N为网络拓扑中节点的个数.

在这个仿真模型中，K定义为0.8，N的范围定义为100∼1000，L根据节点的平均度数D决定.根据拓扑中包含的节点数目的不同，我们设定D为7，最大不超过10.

仿真具体由两个实验完成.实验时，分别在节点规模为100∼1000时进行测试，相同的节点规模测试10次，求其平均值作为实验值.实验1比较边权值变化时IDEW-SPT算法和[12]算法在更新SPT时花费时间的不同.实验2比较边权值变化时IDEW-SPT算法和[12]算法更新SPT时更新节点的总次数.具体实验如下：

实验1由于每一次更新SPT的时间非常短，因此实验中给出的数据是1万次更新时间的总和，时间单位为ms.根据产生的拓扑以及变化，采用[12]算法和IDEW-SPT算法更新已有SPT，仿真结果如图1所示.其中黑线为IDEW-SPT算法花费的时间，蓝线为[12]算法花费的时间.根据图1可知，[12]算法更新1万次用时在30ms到40ms之间，而IDEW-SPT算法在15ms到32ms之间.由实验数据可以得出，在边权值变化时，更新1万次花费的时间总和IDEW-SPT算法比[12]算法平均少38%.

实验2本实验比较节点规模为100∼1000时，IDEW-SPT算法和[12]算法更新SPT时节点更新的总次数，即所有节点更新次数之和.假设一个节点在更新过程中达到最后状态时更新的次数为3，则节点更新总次数增加3.根据产生的拓扑以及变化，仿真结果如图2所示.

根据图2可知，在边权值变化时，更新节点的总次数IDEW-SPT算法比[12]算法平均少31%.

5 结论

本文通过深入分析，提出一种基于可变权值的全动态最短路径算法.该算法根据初始SPT中的信息，结合变化链路在拓扑中的位置，将需要更新的节点和链路控制在较小的范围内，仅考虑和计算在更新过程中会发生变化的节点和链路，在保证节点最短路径计算正确的情况下，有效的降低了冗余计算，减少了更新时间.

图1 算法的时间开销

图2 算法的更新节点总次数