在非对易空间中Aharonov-Bohm效应和中性粒子的量子相位∗

阿布都外力·艾尼瓦尔，孙冬婷，路彬彬，江涛，贾振红

(1.乌鲁木齐民族干部学院，新疆乌鲁木齐830002；2.新疆大学信息科学与工程学院，新疆乌鲁木齐830046)

0 引言

近年来，自从弦理论与非对易理论之间的关系被揭示以后，有关非对易空间各种物理问题的研究引起了理论物理学界的广泛关注[1−4].在弦的尺度或高能条件下（TeV或更高的能量）时空会显出其非对易性质，因此对时空非对易性产生的物理效应的研究是近期理论物理领域的热门课题.最近，除了量子场论中的问题以外，量子力学的很多问题也引起了理论物理学界的广泛关注[5−9].在通常的对易空间中，国内外此类问题已研究的比较成熟.近年来随着对非对易时空的认识不断深入，很多物理学家又重新将这些问题放在非对易背景下研究，得到了与非对易性有关的一些重要结论，而这些结论又进一步加深了我们对非对易效应本质的认识.很多情况下，人们开始在非对易空间中研究有关量子相位的问题.如Aharonov-Bohm效应（AB效应）和Aharonov-Casher效应（AC效应）在非对易空间中以及非对易相空间中已开始进一步研究[10−18].文献[10-12]详细的研究了在非对易空间中和非对易相空间中AB效应；在非对易空间和非对易相空间中的AC效应以及在非对易量子力学中的He-McKellar-Wilkens效应（HMW效应）在文献[13-17]中详细地研究过；非对易量子霍尔效应在文献[18-20]中被详细地讨论了；在文献[21]中作者详细地研究了在电磁场中运动的且具有电偶极矩和磁偶极矩的中性粒子的非对易量子力学行为.目前为止，还没有文献专门研究过电四极矩在电磁场中的量子相位问题.所以在非对易情况下研究电四极矩的量子相位是很有意义的.

在前人对非对易时空理论和对粒子的AB效应、AC效应、HMW效应和对具有电四极矩的中性粒子的量子相位已有研究的基础上，本文从非对易量子力学入手，从坐标变换开始，在非对易空间中分别对外场做变换来得到在非对易空间中的对应场，以此研究非对易空间中的AB效应和带电偶极矩，电四极矩和电多极矩的中性粒子的AB相位.这样，避开了星乘积（star product）方法，解决非对易空间中的问题就变得简单多了.

这篇论文的安排如下：在第2节，我们将简短地回顾在对易空间中的AB效应和中性粒子的量子相位；在第3节，我们将通过对外场的变换来得到AB效应和中性粒子的量子相位；在最后一节会给出这篇论文所得到的一些结论.

1 在对易空间中的AB效应和中性粒子的量子相位

AB:1959年,Aharonov和Bohm(AB)[22]提出了与电子的通常的AB效应和电AB效应有关的两类干涉实验.其中通常的AB效应是指，在电子的双缝干涉实验中，若在双缝后面放置一个细长的螺线管，当螺线管通以电流从而在管内产生磁场时，发现干涉条纹移动.按经典力学，由于两束电子束的路径上=0，电子不受Lorentz力，电子的运动不会受影响，原来的两束电子的干涉条纹不会改变.电磁相互作用的一个基本原理是局域相互作用，即某点上的点和电流仅受到该点处场的作用.所以螺线管内的场不可能直接作用到管外的电子上.用经典理论是不能解释电子的这种行为的，这是一种量子效应.虽然螺线管外的磁感应强度B为零，但是矢势=0，矢势可以对电子发生相互作用.因此，AB效应表明矢势具有可观测的物理效应，它可以影响电子波束的相位，从而使干涉条纹发生移动.按量子力学，由于电子Hamiltonian中包含着磁势，两束电子的波函数差一个相位因子，电子之间的干涉条纹发生变化.AB效应的存在说明磁场的物理效应不能完全用来描述.这种量子相位如下给出[22]：

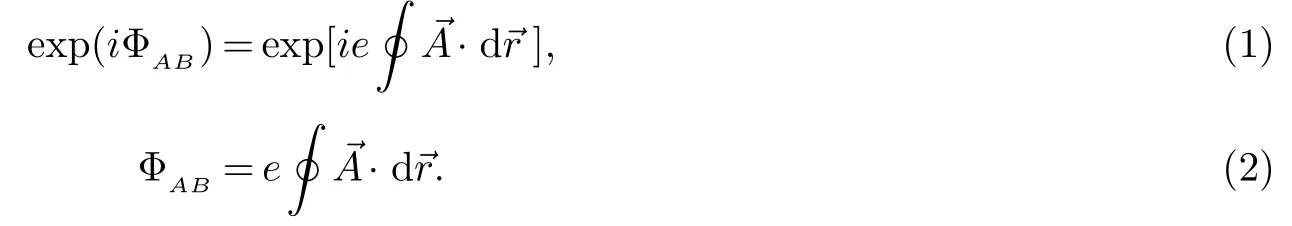
（这里我们用到了 =c=1单位）

另一种是带电粒子的电AB效应.电AB效应是指，带电粒子在电场中所发生的相位是由标势φ(x,t)引起的.这种量子相位如下给出[22]：

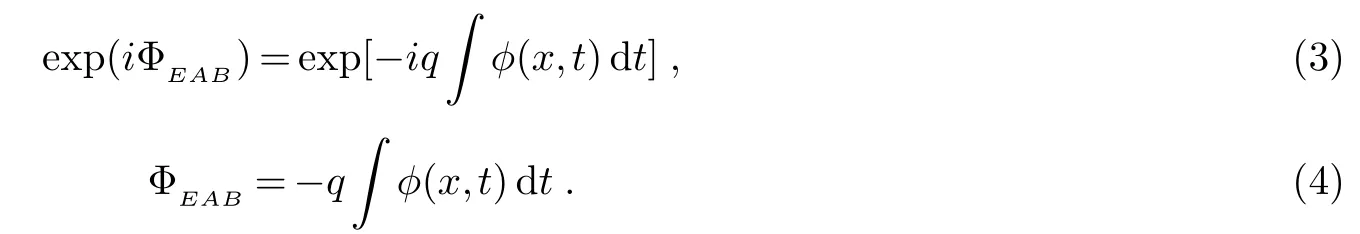
He-McKellar-Wilkens效应（HMW效应）:He，McKellar[23]和Wilkens[24]独立地预言了一种带电偶极矩的中性粒子的量子相位，即当中性粒子环绕平行于其电偶极矩方向的线磁荷（沿一条直线分布的磁单极子）运动时，将会产生类似于AB效应中的量子相位.这种量子相位如下给出[24]：

带电四极矩和电多极矩的中性粒子的量子相位：1995年，Chia-Chu Chen[25]在通常的对易空间中研究并预言了带电四极矩和电多极矩的中性粒子的AB相位.他提出，AB相位可以发生在两个简单的电荷分布，即单极和偶极矩情况.他进一步地预言了这种量子相位对于多极矩展开也是普遍存在的.

当粒子处于静止的时候，粒子在电磁场中的势能可写为：

很显然，这里的Qij是无迹的对称张量.

对于在电磁场中运动的带电四极矩的中性粒子，这种量子相位给出如下[25]:

如果我们考虑到q=0，=0和Qij=0的情况，即只有粒子的电多极矩Mi1···in∂i1.于是，在电磁场中对带电多极矩的中性粒子来说其相互作用能为：

同样，这里的Mi1···in也是无迹的对称张量.

对于在电磁场中运动的带电多极矩的中性粒子，这种量子相位如下给出：

2 在非对易空间中的AB效应和中性粒子的量子相位

上节我们简短地回顾了在通常对易空间中的AB效应和中性粒子的量子相位.现在我们在非对易空间中对这些效应进行进一步的研究.

首先，我们要简短的介绍一下非对易空间的一些性质.在弦尺度下，不仅坐标与动量不对易，而且出现了空间的非对易效应，即坐标与坐标不再对易的情况.所以非对易空间是一个坐标i与动量i算符满足以下对易关系的空间：

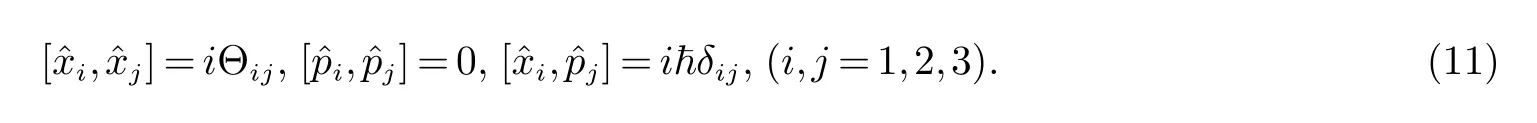
这里xi和pi是在通常的量子力学中的坐标和动量算符.

现在我们开始讨论非对易空间中的AB效应和中性粒子的量子相位.在非对易空间中研究这些问题，目前有三种方法：第一种是，在非对易空间中建立薛定谔方程，利用星乘积（star product）方法来解方程.即通过用非对易空间中的星乘积来代替对易空间中通常的乘积来写出在非对易空间中的薛定谔方程.然后，解此薛定谔方程来得到相位.如，在非对易空间中的薛定谔方程为：

这里H(x,p)是系统在对易空间中的哈密顿量.这里的Moyal-Weyl乘积（星乘积）被定义为：

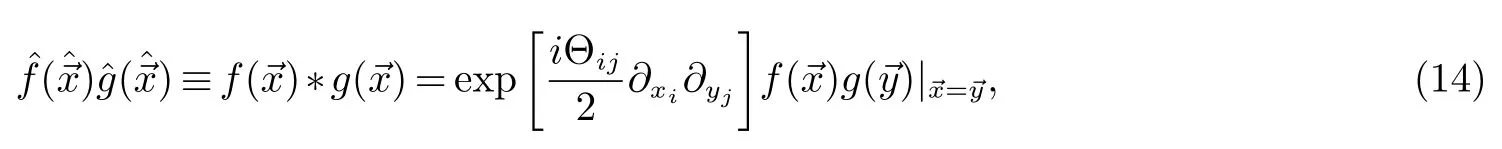
第二种是：利用Bopp’s变换，在非对易空间中的星乘积可以改为通常的乘积.即通过在对易空间中的哈密顿量H(x,p)与在非对易空间中的哈密顿量H替换来把星乘积改为通常的乘积.因此，薛定谔方程可以写成：注意到方程（15）是被在对易空间中定义的.然后，在对易空间中解此薛定谔方程来得到相位.非对易效应可以通过有关Θ的项来表现出来.

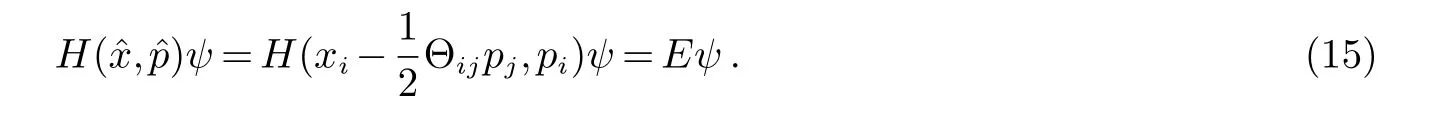
第三种方法比前两种方法简单、方便而且可以避免复杂的星乘积的计算，大大减轻计算量.即，在前人对AB效应和中性粒子的量子相位已有研究的基础上，我们在非对易空间中研究问题，仅需要分别对外场做变换，就能得到在非对易空间中的其相对应的量子相位.

即在电磁场存在的情况下，我们还需要对电磁场作如下的变换：

2.1 在非对易空间中的AB效应

按照上面介绍的第三种方法，我们通过对在非对易空间中的磁势做个变换来得到在非对易空间中的AB效应的量子相位.即，将方程（16）代入到方程（2）中，我们得到（这里我们用到 =c=1单位制），

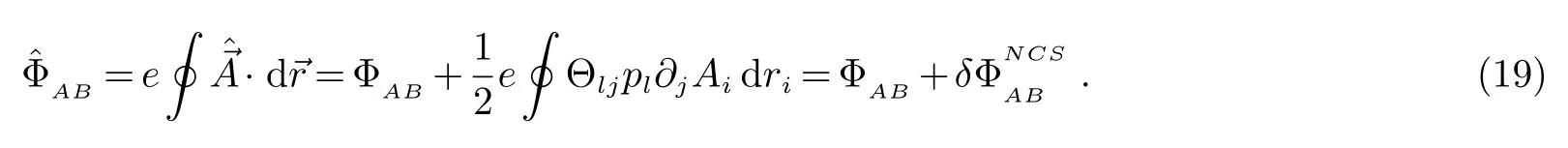
这是带电粒子在非对易空间中的AB相位.这里第一项ΦAB是带电粒子在对易空间中的AB相位；第二项是空间非对易所导致的附加项.它们如下给出：

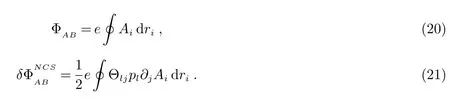
在三维非对易空间中,i,j=1,2,3,我们可以定义一个矢量θ=(θ1,θ2,θ3),这里的θi满足Θij=ijkθk或者因此，方程（19）可写成：

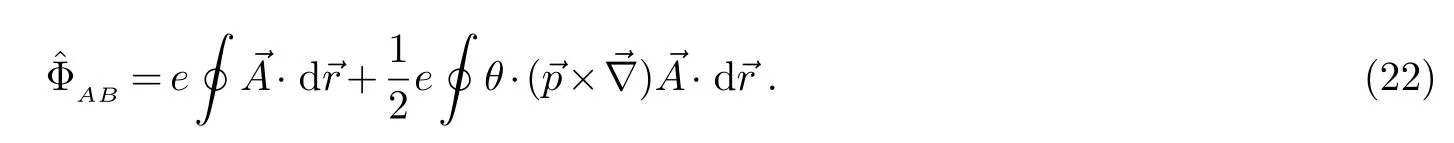
其中是带电粒子的动量.其非对易性质是通过有关θ的第二项表现出来的.从上式可以明显地看出，若非对易参数θ=0，则在非对易空间中带电粒子的AB相位跟对易空间中带电粒子的AB相位结果一致(方程(2)).

2.2 在非对易空间中的电AB效应

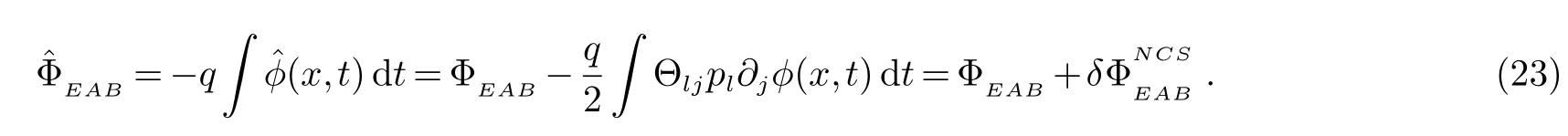
其中q是带电粒子的电荷量.这是带电粒子在非对易空间中的电AB相位.这里第一项ΦEAB是带电粒子在对易空间中的电AB相位；第二项是空间非对易性所导致的附加项.它们如下给出：

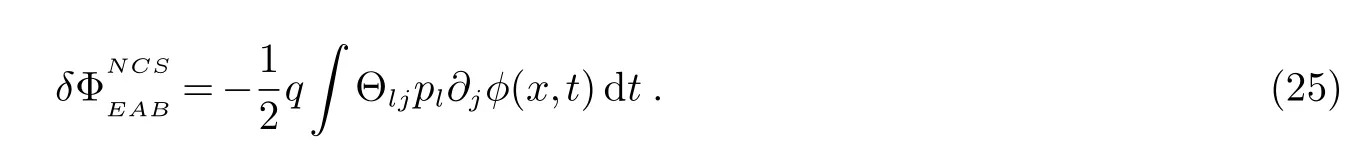
在三维非对易空间中，方程（23）可写成：

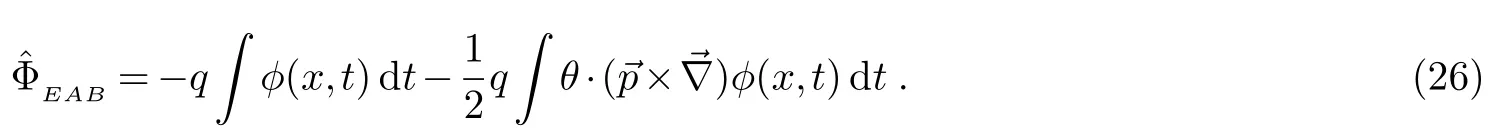
上式的非对易性质是通过有关θ的第二项而表现出来的.从上式可以明显地看出，若非对易参数θ=0，则在非对易空间中带电粒子的电AB相位跟对易空间中带电粒子的电AB相位结果一致(方程(4)).

2.3 在非对易空间中的HMW效应

现在我们在非对易空间中讨论一下带电偶极矩的中性粒子在磁场中运动情况下的HMW效应，即带电偶极矩的中性粒子在磁场中所产生的AB相位.同样的方法，我们通过对在非对易空间中的做个变换来得到在非对易空间中的带电偶极矩的中性粒子的AB相位.通过将方程（17）代入到方程（5）中，我们可以得到，

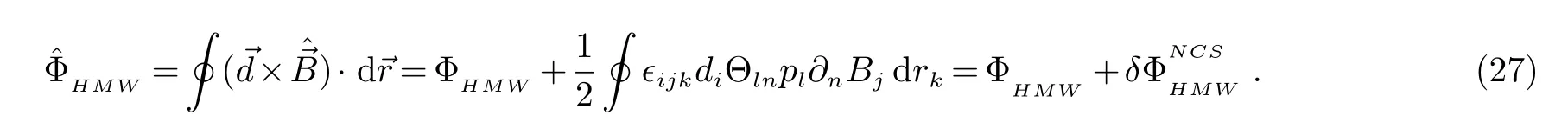
得到的这个相位是带电偶极矩的中性粒子在非对易空间中的电AB相位.这里第一项ΦHMW是带电偶极矩的中性粒子在对易空间中的电AB相位；第二项是空间非对易所导致的附加项.它们如下给出：

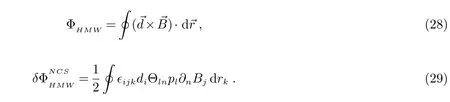
在三维非对易空间中，方程（27）可写成：

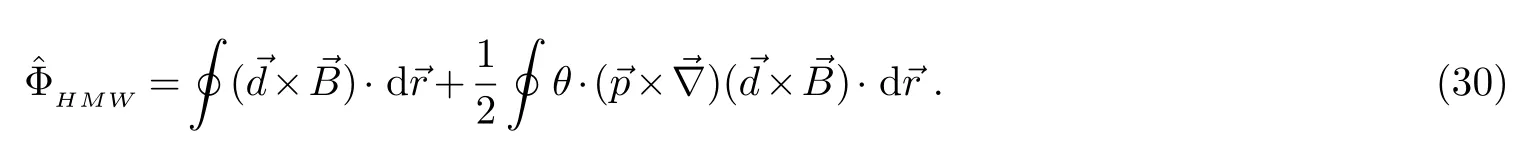
这个相位是带电偶极矩的中性粒子在三维非对易空间中的电AB相位.这里第一项是带电偶极矩的中性粒子在对易空间中的电AB相位；整个相位的非对易性质是通过有关θ的第二项表现出来的.从上式可以明显地看出，若非对易参数θ=0，则在非对易空间中带电偶极矩的中性粒子的电AB相位跟在对易空间中带电偶极矩的中性粒子的电AB相位结果一致(方程(5)).

2.4 在非对易空间中带电四极矩或电多极矩的中性粒子的电AB相位

在电磁场中运动的带电粒子将会产生AB相位（AB效应）；在电磁场中运动的带电偶极矩的中性粒子同样会产生AB相位（HMW效应）;那么，在电磁场中运动的带电四极矩或者电多极矩的中性粒子也会产生AB相位吗？这就是Chia-Chu Chen[25]所研究的问题，他预言了这种相位将会存在.这个问题我们在第二节中讨论过.根据Chia-Chu Chen在对易空间中的所得到的研究结果的基础上，我们把这些结果推广到非对易空间中.

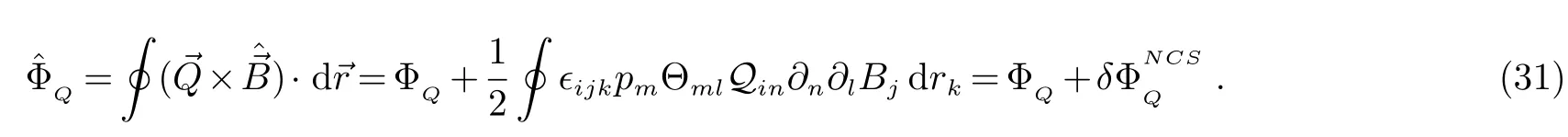
这是带电四极矩的中性粒子在非对易空间中的AB相位.这里第一项Q是带电四极矩的中性粒子在对易空间中的AB相位；第二项是空间不对易而引起的附加项.它们如下给出：

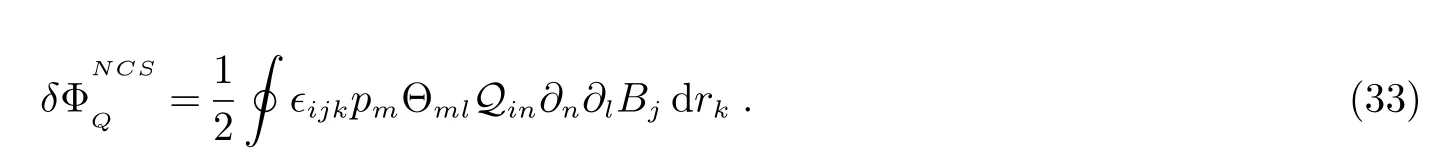
在三维非对易空间中，方程（31）可写成：

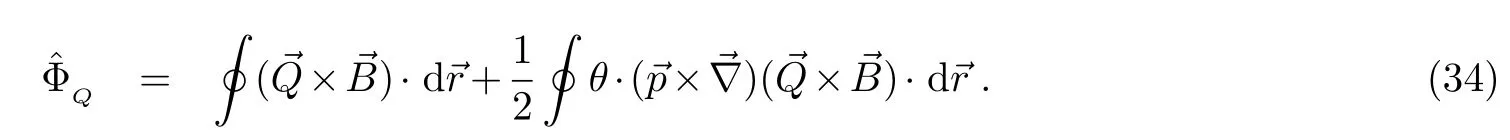
这是带电四极矩的中性粒子在三维非对易空间中的AB相位.上式的第一项是带电四极矩的中性粒子在对易空间中的AB相位.其非对易性质是通过有关θ的第二项来表现出来.从上式可以明显地看出，若非对易参数θ=0，则在非对易空间中带电粒子的AB相位跟对易空间中带电粒子的AB相位结果一致(方程(8)).

现在我们把这些结果推广到带电多极矩的中性粒子的情况.利用同样的方法，我们通过对在非对易空间中的做个变换来得到在非对易空间中的带电多极矩的中性粒子的AB相位.通过将方程（17）代入到方程（10）中，我们可以得到，

其中：

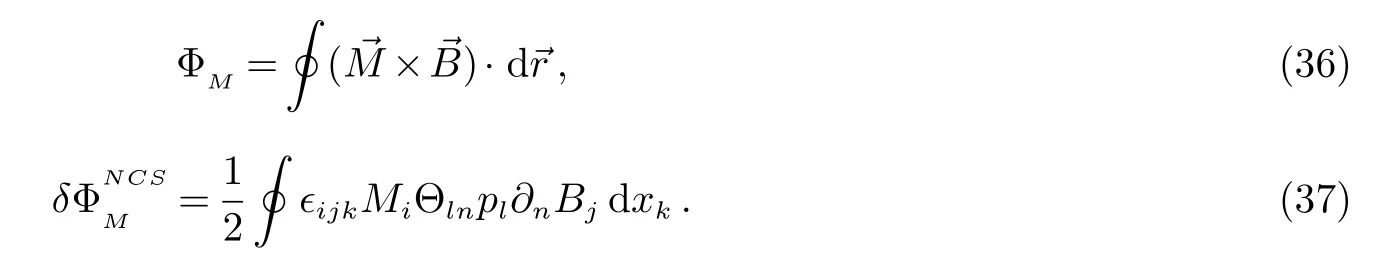
方程（35）给出的相位是带电多极矩的中性粒子在非对易空间中的AB相位.这里第一项ΦM是带电多极矩的中性粒子在对易空间中的AB相位；第二项是空间非对易性所导致的附加项.在非对易空间中带电多极矩的中性粒子的AB相位的非对易性质可以通过有关θ的第二项表现出来.

在三维非对易空间中，方程（35）可写成：

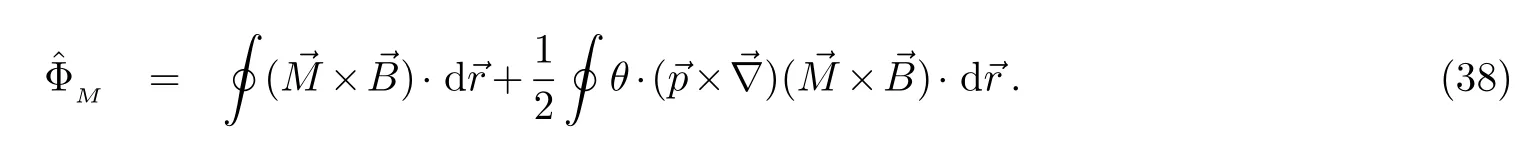
这个相位是带电多极矩的中性粒子在三维非对易空间中的电AB相位.这里第一项是带电多极矩的中性粒子在对易空间中的电AB相位.其中的非对易性质是通过有关θ的第二项表现出来的.从上式明显地看出来，若非对易参数θ=0，则在非对易空间中带电多极矩的中性粒子的电AB相位跟在对易空间中带电多极矩的中性粒子的电AB相位结果一致(方程(10)).

3 结论

论文研究了非对易空间中的AB效应以及带电偶极矩、电四极矩和电多极矩的中性粒子的AB相位.首先，在第1，2节中我们简单地回顾了这些问题在对易空间中的已有的研究结果；在第3节，首先简短地介绍了非对易空间的一些性质，并且更进一步提出了我们用于处理非对易量子力学中的问题的三种方法.进而按照我们提出的第三种方法来研究在非对易空间中的AB效应以及带电偶极矩、电四极矩和电多极矩的中性粒子的AB相位问题.相比前两种方法，这种方法简单、方便并且可以避免复杂的星乘积的计算，大大减少计算量.根据这种方法，在前人对AB效应和中性粒子的AB相位已有研究的基础上，我们在非对易空间中研究问题，仅仅通过分别对外场做变换就可以分别得到在非对易空间中的AB效应和带电偶极矩、电四极矩和电多极矩的中性粒子的AB相位.

在非对易空间中，我们得到的结果(方程(19),(23),(27),(31)和(35))跟对易空间中的结果是有所区别的(方程(2),(4),(5),(8)和(10)).在非对易空间中，我们所得到的各相位都由两项构成：第一项是在对易空间中的AB效应和带电偶极矩、电四极矩和电多极矩的中性粒子的AB相位；有关θ的第二修正项和是空间非对易所引起的附加修正项.显然，若非对易参数θ=0，则在非对易空间中的结果跟在对易空间中结果将会一致(式(方程(2),(4),(5),(8),(10)).

假如目前关于AB效应和带电偶极矩、电四极矩和电多极矩的中性粒子的AB相位的实验条件允许的话，可以利用这些实验测量估计非对易参数θ的大小.我们得出的结论是：如果能对以上量子系统进行精密的测量，则可进一步的揭示、检验空间的非对易性.