组合激光脉冲激发的等离子体尾场的参数研究∗

西日艾·买买提，沙依甫加马力·达吾来提，谢柏松

(1.新疆大学物理科学与技术学院，新疆乌鲁木齐830046；2.北京师范大学核科学与技术学院，北京100875)

0 引言

使用微波技术的传统加速器由于受到其结构的金属材料的电场阈值的限制，加速梯度制约在∼100MeV/m之下[1].这迫使科学家们提出一个新的加速机制来获得较高加速梯度.等离子体可选为理想的加速介质，因为它本身是一个电离的介质，不存在被电场击穿的阈值问题.用电子等离子体波来加速电子的设想是由Tajima和Dawson在1979年首次提出的[2].当激光脉冲在亚临界密度的等离子体中传播时，光脉冲的纵向有质动力会推动等离子体中的电子向前运动，使其偏离原来位置；等离子体中的离子由于质量太大，将几乎保持不动，当激光脉冲超越电子后，由于正负电荷分离而产生的静电力会将电子往平衡位置拉，造成电子在空间的纵向振荡，形成电子等离子体波.由于该等离子体波是由激光脉冲激发且存在于激光脉冲后方，被称为激光尾波，它的相速度与激光脉冲在等离子体中传播的群速度相同；电荷分离所产生的场被称为激光尾波场.它的加速梯度比传统加速器高三个数量级以上，带电粒子可被尾场捕获并在很短的距离内能够达到非常高的速度.伴随着每一次激光技术的革新，激光尾波场加速从理论到实验都得到了飞速发展.由于在实验上已经观察到高能量的准单能电子束[3]，使人们对尾波场加速器的前景充满期待.TeV的能量增益被提上了研究日程.有理由相信，在不远的将来，一种小型的，低廉的，台面型的高能电子加速器将进入普通大学或研究所的实验室.它的出现也必将给高能物理、材料物理、医疗科学、超快电子显微科学，飞秒X射线激光等领域带来飞速发展[4,5].在尾场中粒子的加速跟尾场的最大最小势有关，而尾场势又跟脉冲参数有着密切的关系，因此要寻找尾场势和脉冲参数之间的关系是至关重要的.

本文是在Esirkepov,Bulanov等人[6]研究的带电粒子在对称Gaussian脉冲激发的尾场的第一周期中加速的理论基础上，对两个对称激光脉冲的结合所驱动的尾场的最大最小势和脉冲参数的关系做了进一步的分析.

1 理论模型

在经典电动力学的框架下，质量为m,电荷为−e的电子在尾场中的哈密顿量H如下[7−10]；

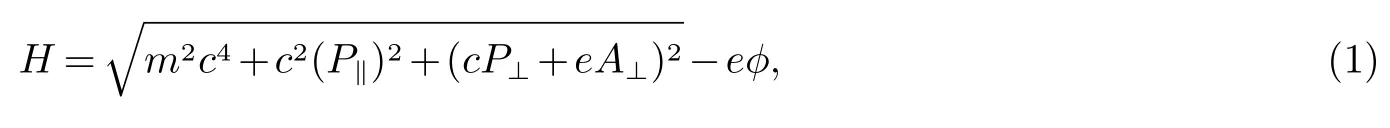
这里和P⊥是归一化动量的两个分量，A⊥是激光脉冲的矢势，φ是尾场矢量.我们可以把哈密顿量在动坐标系X=x−υgt中可重新描叙如下，υg是激光脉冲的群速度，其余尾场的相速度相等.

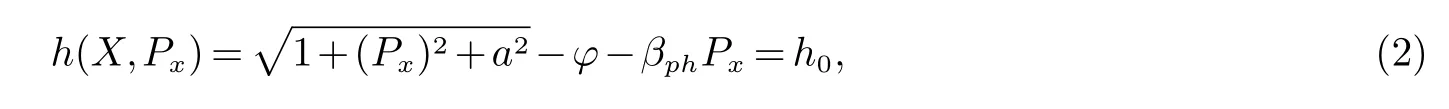
这里h0是一个常数.本文中使用的归一化物理量，比如电子横向动量，激光场矢势，尾场标矢，哈密顿量，尾场波相速度的归一化规则是.式2的解为；

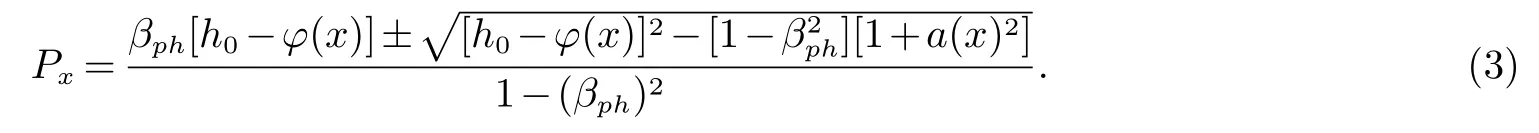
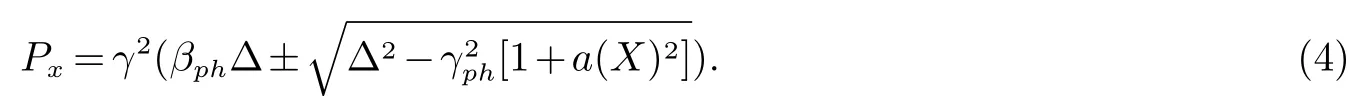
电子获得的能量ε为；

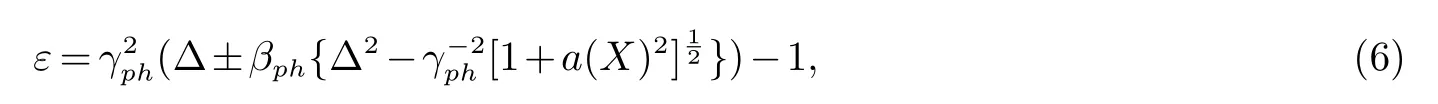
这里”+”对应的随时间增加，”-”对应的随时间减少.

通过式2给出的哈密顿量形式可以写出电子动量的正则方程如下；

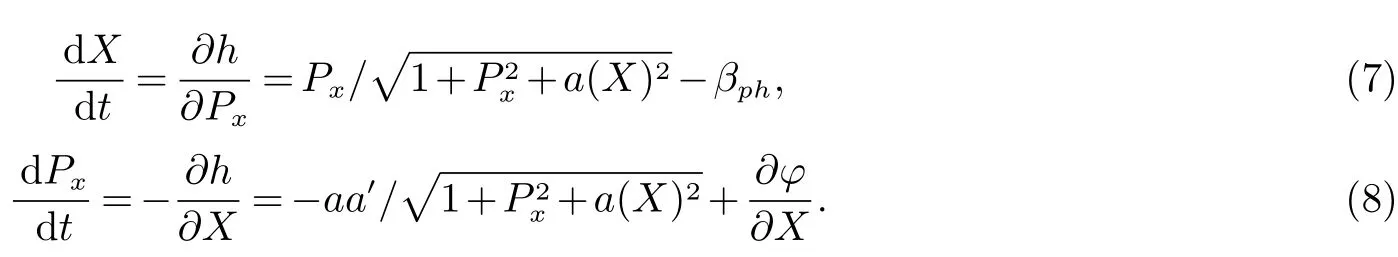
我们用Poisson方程来描述尾场势，

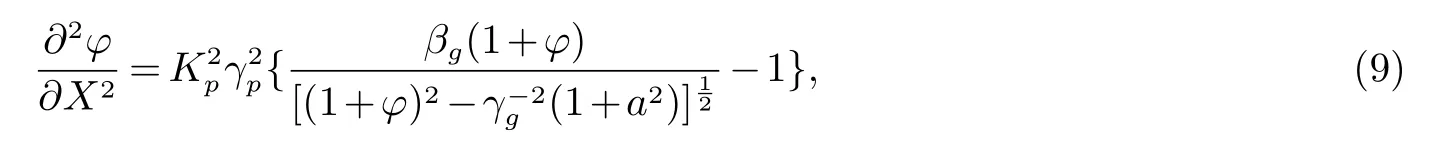
这里Kp=ωp/c.

2 数值计算结果与分析

为了方便起见，本文中使用了对称Gaussian激光脉冲.脉冲的数学表达式为.这里a01，a02代表脉冲a1和a2的最大强度.L1，L2是以激光波长归一化的激光脉冲宽度.k1，k2是可以确定激光脉冲包络顶端平滑程度的参数，比如当k=1（k=k1=k2）时激光脉冲是标准的Gaussian,当k1时激光脉冲是个方波.两个组合脉冲之间的距离（两个脉冲波峰间的距离）定为X0=L1/2+L2/2.因为激光有质动力跟组合激光的平均强度有关，所以我们得到：

和

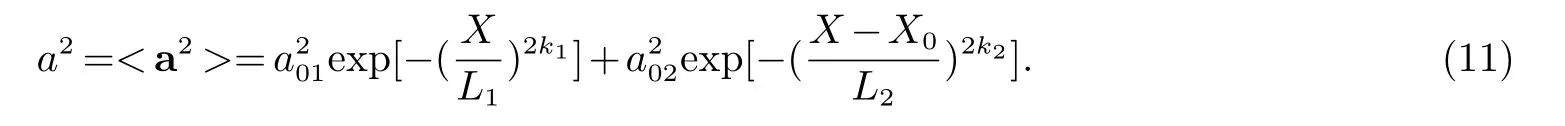
这里a1为强激光脉冲，a2为弱激光脉冲.我们考虑这两个激光脉冲的组合激光脉冲为a（见图1）.为了方便，在本文中激光脉冲的两种组合情况用符号a1a2（a1脉冲在前，a2脉冲在后）和a2a1（a2脉冲在前，a1脉冲在后）表示.

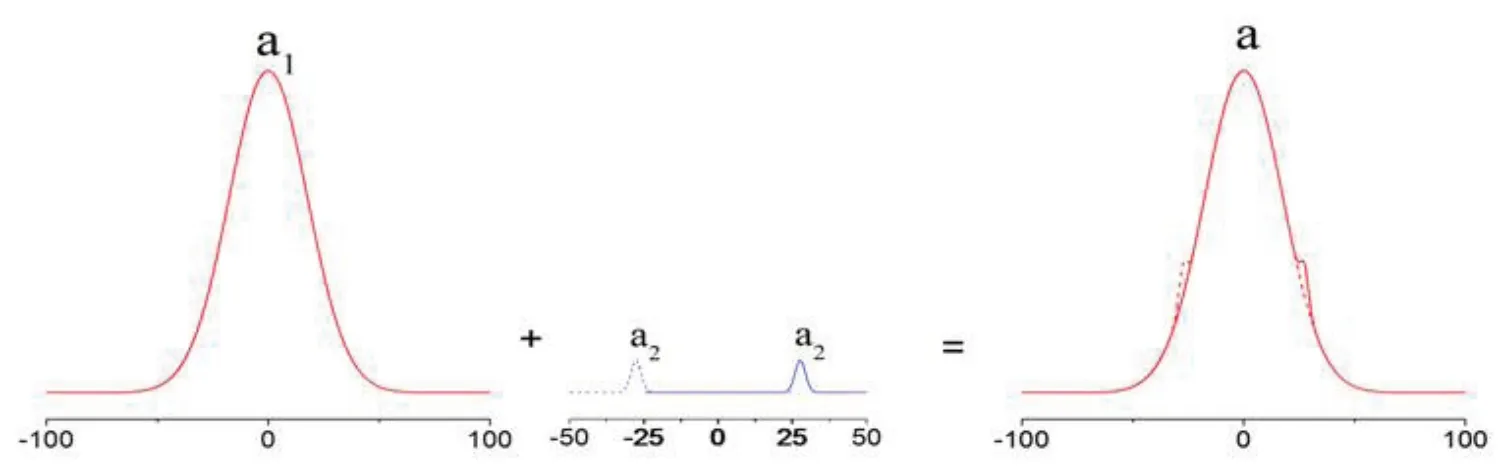
图1 显示弱脉冲a2加在强脉冲a1的前面后面的情况，这里a02=a01=a01

我们再考虑两个脉冲宽度L1和L2在四种不同情况下的组合对尾场的影响（见图2）.

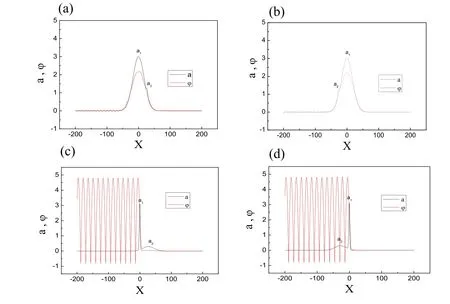
图2 两个激光脉冲的各种组合下被激发的尾场的对比.(a)和(c)是a2a1情况，(b)和(d)是a1a2情况.各激光脉冲参数如下：a01=3,a02=0.3,k1=1,k2=1;对(a)和(b)L1=25,L2=2.5;对(c)和(d)L1=2.5,L2=25

由图2可知，a2加在主脉冲a1后面的情况（a1a2情况）被激发的尾场势几乎是完全对称的，跟单个激光脉冲a1激发的尾场一样的（见图2(b)和2(d)）.而a2加在强激光脉冲a1前面时尾场势的最大值偏离中心点往小脉冲方向移动（见图2(a)和2(c)）.这说明小的激光脉冲激发的尾场被强激光脉冲调制，形成了不对称的激光尾场.而加在后面的小脉冲激发的场影响不到前面主脉冲所形成的尾常 所以a1激发的尾场几乎不变.图2(c)和2(d)中因为主脉冲a1非常短，被激发的尾场势很大.但是，尾场长度很短，也不利于有效的加速带电粒子.

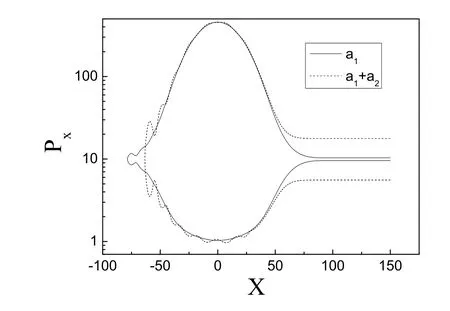
图3 被加速电子的动量相图.a2a1情况，L1=25,L2=2.5，k1=k2=1

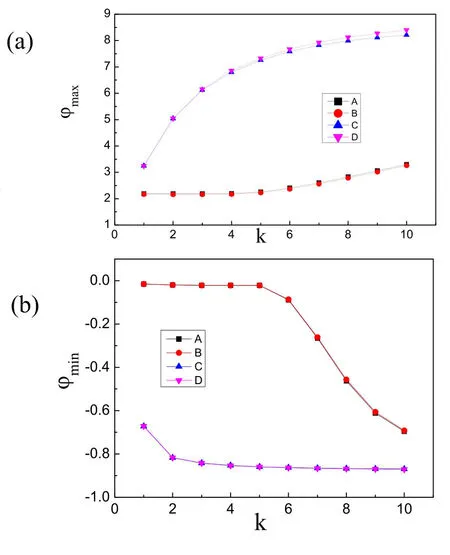
图4 尾场势ϕ和对称高斯脉冲参数k之间的关系.A,B,C,D等四种情况分别指定的激光脉冲宽度和脉冲组合顺序跟图2里的(a),(b),(c)和(d)一一对应

图3 中显示了单个脉冲（实线）和组合脉冲（虚线）激发的尾场中被加速电子的动量相图.图3中可以看出组合脉冲（a2a1情况）激发的尾场对电子加速的效果跟单个脉冲a1激发的尾场的加速效果比较提高了很多.这个结果跟我们在上面提到的尾场势在组合脉冲条件下（图2(a),a2a1情况）被调制优化了电子在尾场中被加速的效率分析一致.

因尾场加速的效率跟组合脉冲的各参数有关，所以有必要讨论尾场势的最大值ϕmax或者最小值ϕmin与激光参数之间的关系.首先研究k对尾场势的影响.图4（a）显示ϕmax和k之间的关系.a1是长脉冲时（L1=25），短脉冲a2（L2=2.5）加在a1前面或后面对尾场势最大值ϕmax随k的变化没有太大的影响.于k=5之前变化非常缓慢，从k=5开始随着k的增大逐渐增大；a1是短脉冲时（L1=2.5），尾场势最大值ϕmax在a1a2和a2a1两种情况在k=5之前都不会有太大的区别，k=5之后两条线就分开了.图4（b）显示ϕmin和k之间的关系.可以看出，a1是长脉冲还是短脉冲，a1a2和a2a1两种情况下的尾场势最小值ϕmin随k的变化趋势是一样的.当a1是长脉冲时（L1=25）在k=5之前随着k的增大尾场势最小值ϕmin不会有太大的变化，k=5后就急剧下降；当a1是短脉冲时（L1=2.5）ϕmin在k=5之前缓慢下降，在k=5后基本不再变化.

图5显示尾场势ϕ和弱脉冲a2的脉冲宽度L2之间的关系.由图5可知，主脉冲a1的脉冲宽度L1固定的情况下，辅助脉冲a2的脉冲宽度L2的变化对尾场势最大值ϕmax和最小值ϕmin引起不了多大的作用.

图6显示尾场势ϕ和主脉冲a1的脉冲宽度L1之间的关系，这里辅助脉冲a2的脉冲宽度定为L2=0.1.由图6可知，当L1逐渐增大到L1=5之前尾场势的最大值ϕmax和最小值ϕmin的变化跟L1的变化有着线性关系，然而当L1≥5之后尾场势ϕ的曲线基本扁平保持不变.

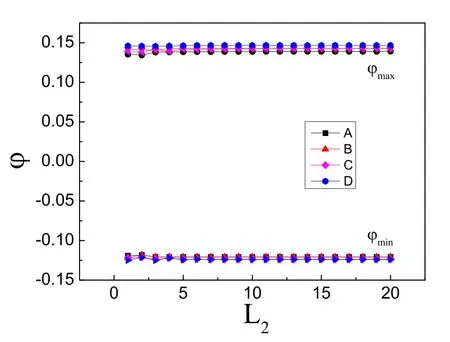
图5 ϕ和L2之间的关系.L1=0.1,a01=1,a02=0.1；A:k=1,a1a2情况;B:k=1,a2a1情况;C:k=2,a1a2情况;D:k=2,a2a1情况

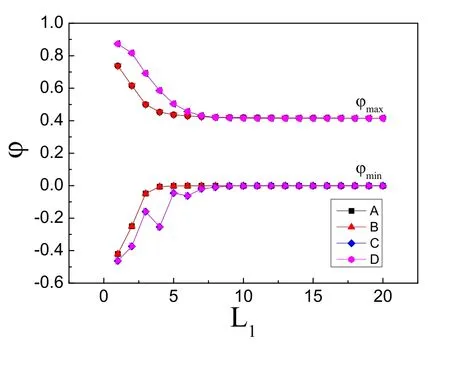
图6 ϕ和L1的关系.L2=0.1,a01=1,a02=0.1.A,B,C和D的参数取值跟图5相同

图7 显示尾场势ϕ和主脉冲a1的最大脉冲强度a01之间的关系.由图7（a）和7（b）中看出，尾场势的最大值ϕmax和最小值ϕmin随a01的变化曲线对a1a2和a2a1情况下没有明显区别.图7（a）显示ϕmax随着a01的增大而增大.当主脉冲a1是短脉冲时这种变化趋势更加明显，而且k=2时的曲线比k=2时的曲线更陡一些.图7（b）显示ϕmin随着a01的增大而减少.脉冲参数选取为L1=2.5，k=2时ϕmin下降的更快.

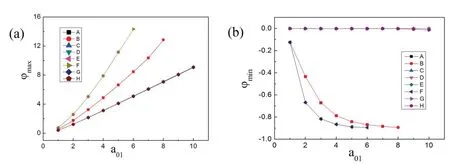
图7 尾场势ϕ和对称高斯激光脉冲振幅a01之间的关系，a02=0.1.A:L1=2.5,L2=25,k=1,a1a2情况;B:L1=2.5,L2=25,k=1,a2a1情况;C:L1=25,L2=2.5,k=1,a1a2情况;D:L1=25,L2=2.5,k=1,a2a1情况;E:L1=2.5,L2=25,k=2,a1a2情况;F:L1=2.5,L2=25,k=2,a2a1情况;G:L1=25,L2=2.5,k=2,a1a2情况;H:L1=25,L2=2.5,k=2,a2a1情况

3 结论

分析了电子在组合脉冲激发的尾场中加速问题.数值计算结果表明，一个在强脉冲a1前面的辅助脉冲a2有助于提高尾场加速的效率.这个效应应该归结为前面跑的脉冲跟等离子体的相互作用帮助调节尾场势，使其更加有利于加速.分析了脉冲包络顶端平滑程度的参数k和脉冲宽度L对尾场势之间的关系.k=5点以后尾场势ϕ随着k的增加而增加的趋势更加明显.辅助脉冲a2的脉冲宽度L2的变化对尾场势的最大值ϕmax和最小值ϕmin的影响很校 由主脉冲a1的脉冲宽度L1和振幅a01来决定.