Stability Analysis of an HIV/AIDS Model with Vertical Transmission∗

Zohragul Osman,Xamxinur Abdurahman

(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract: This paper considers an HIV/AIDS epidemic model with treatment and vertical transmission.The equilibrium points of the model are found and their stability is investigated.The model exists two equilibria namely,the disease-free and endemic equilibrium.It is found that if the basic reproduction number R0<1 the disease free equilibrium is globally asymptotically stable and in such a case the endemic equilibrium does not exist.Where as the unique infected equilibrium is globally asymptotically stable if R0>1.

Key words:HIV/AIDS epidemic model;Vertical transmission;Basic reproduction number

0 Introduction

TheHIV/AIDShas become an important infectious disease in both developing and developed nations.It is a fatal disease,which can breaks down the body’s immune system,leaving the victim vulnerable to a host of millions of life threatening opportunistic infectious,neurological disorder or unusual malignancies.So the study toHIV/AIDStransmission dynamics has been of great interest to both applied mathematicians and biologists due to its universal threat to humanity.Mathematical models have been used extensively in research into the epidemiology ofHIV/AIDSto help improve our understanding of the major contributing factors to the pandemic.Some classicHIVmodels are introduced in[1-8].Vertical transmission can be accomplished through transplacental transfer of disease agents.In recent years a few studies of vertical transmission have been conducted to describe the effects of various epidemiological and demographical factors[9-12].

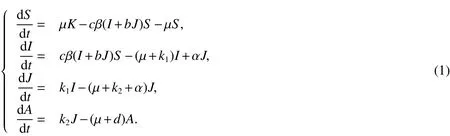
In[1],L.Cai and X.Li studied local and global stability of the equilibria of aS IJAmodel with treatment methods.It is assumed that some individuals with the symptomatic phasesJcan be transformed into asymptomatic individualsIafter treatment and model is given by the following system:

In[5],Ram Naresh et al.considered the followingS IPAmodel with treatment and vertical transmission:

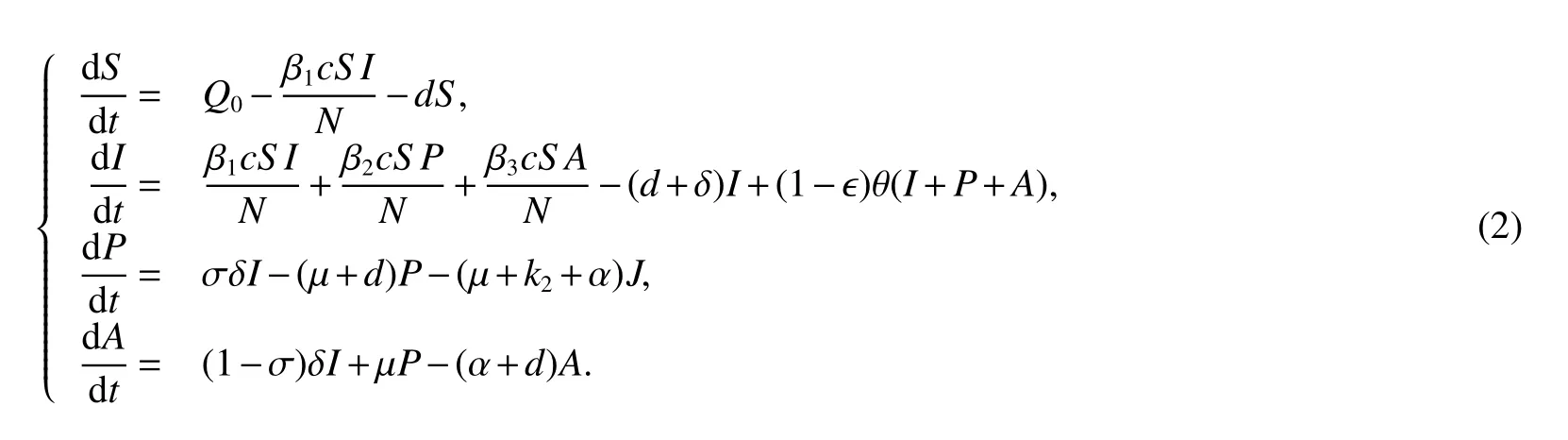
Here,the authors assumed that the pre-AIDSpatients(P)andAIDSpatients(A)are sexually inactive as they are isolated and hence are not capable of producing children,that is(1− )θP=(1− )θA=0.They also do not contribute to viral transmission horizontally,that is β2and β3are taken negligible.The authors proved the local and global stability of disease free equilibrium and endemic equilibrium considering these assumptions and under some other conditions.

Based on the model(1)and(2),we consider a new model,in which we further assume that vertical transmission of infectives and pre-AIDSpatients can back to the infective stage by treatment and(1− )θP0 which means that some of the pre-AIDSpatients’children also can effect the infectives.

The organization of the paper is as follows.In the next section we present the model with vertical transmission.Section 3 presents some basic results of the model.In Section 4,we analyze the equilibrium points of model and their local and global stability.Section 5 presents the discussion.

1 Mathematical model

Assume that the populationNis divided into four subclasses:the susceptibles(S),the infectives(I),the pre-AIDSpatients(P)andAIDSpatients(A).We further assume that the susceptibles becomeHIVinfected via sexual contacts with infectives,a fraction of new born children are infected at birth and hence are directly recruited into the infective class with a rate(1− )θ and others die effectively at birth(0≤ ≤1).The infectives through vertical transmission at any time t is given by(1− )θ(I+P+A).With the above considerations and assumptions,the spread of the disease is assumed to be governed by the following model:

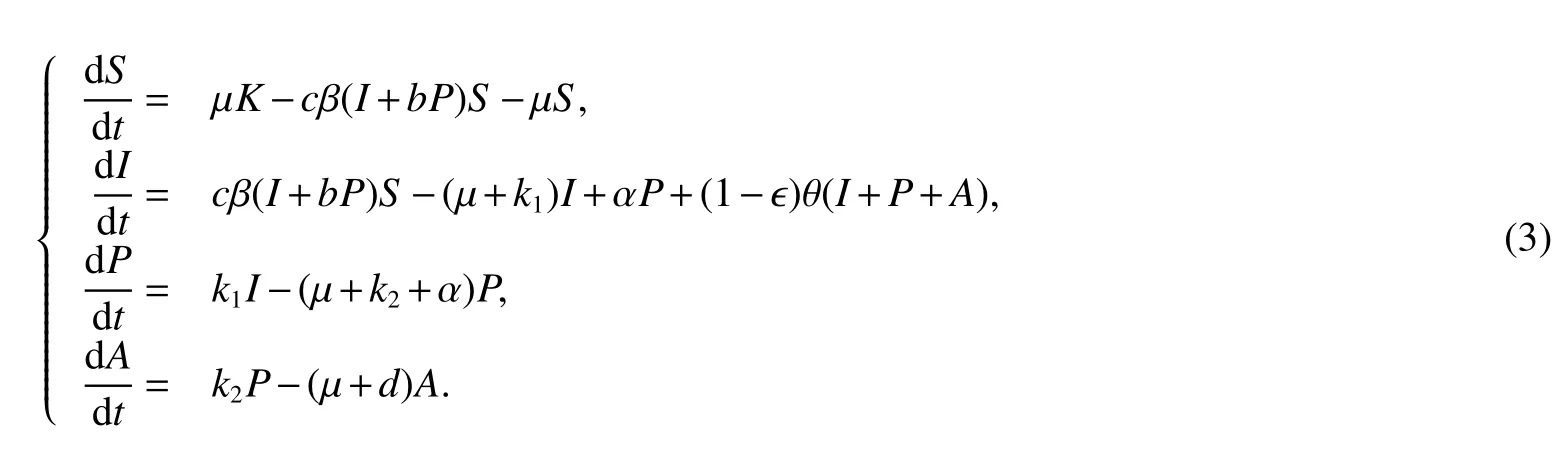
WhereµKis the recruiment rate of the population,µ is the death rate constant.cis the average number of contacts of an individual per unit of time.β andbβ are probablity of disease transmission per contact by infectives and pre-AIDSpatients.k1andk2are transfer rate constants from the infective phaseIto the pre-AIDSphasePand from the pre-AIDSphase to theAIDSphase,respectively.α is treatment rate from the pre-AIDS Pto infective phaseI.dis the disease-related death rate of theAIDScases.θ is the birth rate coefficient of newborns,(1− )is the fraction of infected newborns joining the infective class after getting sexual maturity to become infectious.It is also assumed that all the dependent parameters of the model are non-negative.

To simplify the model,it is reasonable to assume that theAIDSpatients are exposed and sexually inactive as they are isolated and hence are not capable of producing children that is(1− )θA=0.Then model(3)can be rewritten as follows:

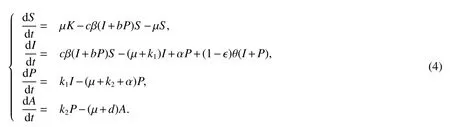
For the model(4),we have the following initial conditions:S(0)=S0,I(0)=I0,P(0)=P0,A(0)=A0.

2 Basic results

In this section we will study the basic properties of model(4).For the positivity of the solution to model(4),we have the following result.

Lemma 1IfS(0)≥0,I(0)≥0,P(0)≥0,A(0)≥0,the solution(S(t),I(t),P(t),A(t))of the model(4)remain positive for all timet>0.

ProofFrom the first equation of(4),we have

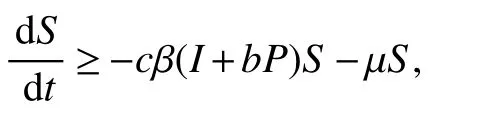
from which we get,

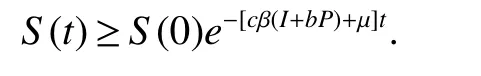
Obviously,S(t)>0 for allt>0 whenS(0)>0.Next,letm(t)=mint≥0{I(t),P(t),A(t)}.Assume that there exists the first timet1such thatm(t)>0 whent∈(0,t1)butm(t1)=0.Ifm(t1)=I(t1)=0,then by the definition of derivativefrom the second equation of(4)we can get thatwhich is a contradiction.This means thatI(t)≥0 for allt>0.From the third and fourth equation of model(4),we easily can prove the positivity ofP(t)andA(t).

Now we will consider the region of attraction of model(4),stated in the form of the following Lemma.

Lemma 2Ifµ>θ,then all solutions of model(4)starting inR3+are bounded and eventually enter the attracting set Ω,here

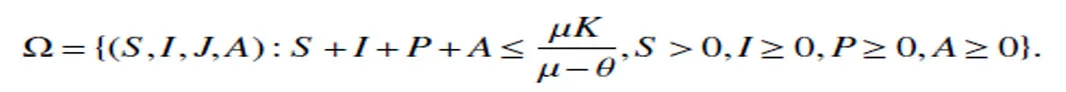
ProofLetN=S+I+P+A,then

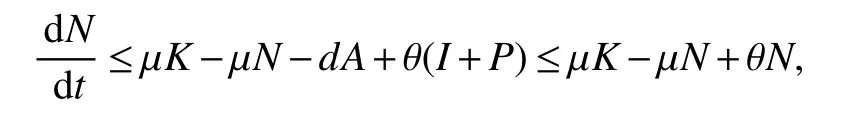
Which gives,

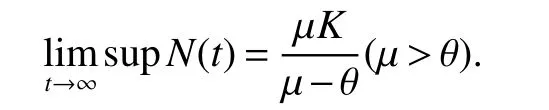
This implies that the invariant region for model(4)is Ω.

It is reasonable to assume thatµ>θ,because constantµ is the death rate,θ is the birth rate of infected newborns.In many epidemic models,it is assumed that the death rate and the birth rate are equal.However,in our model,the birth rate of infected newborns θ is smaller than the birth rate,thus in the following we assume thatµ > θ.

3 Equilibria and their stability

Since the variableAof model(4)does not appear in the first three equations,in the subsequent analysis,we only consider the submodel:

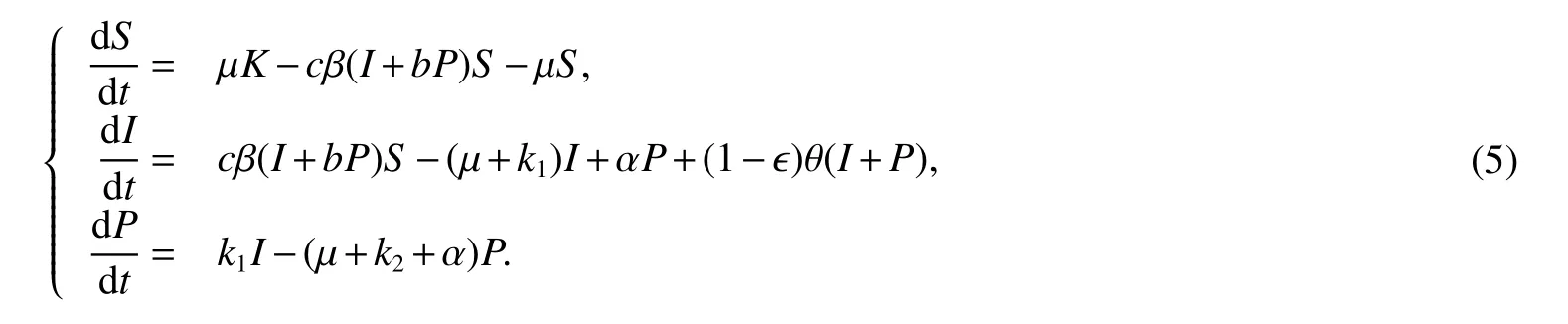
Model(5)always has a disease-free equilibriumE0=(K,0,0).

Letu=(I,P,S)T,model(5)can be written as

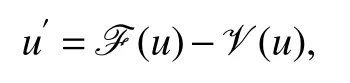
where

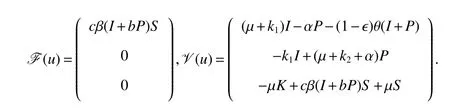
The Jacobian matrices ofF(u)andV(u)at the disease-free equilibriumE0are,respectively,

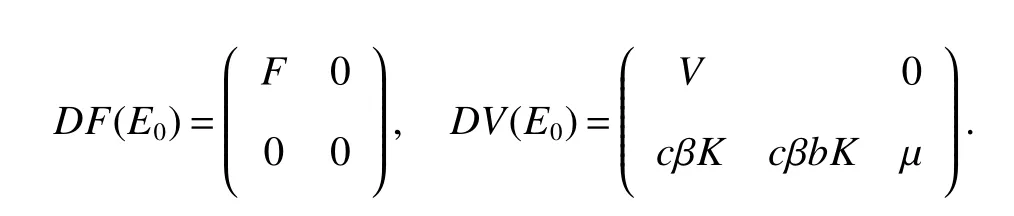
Where,

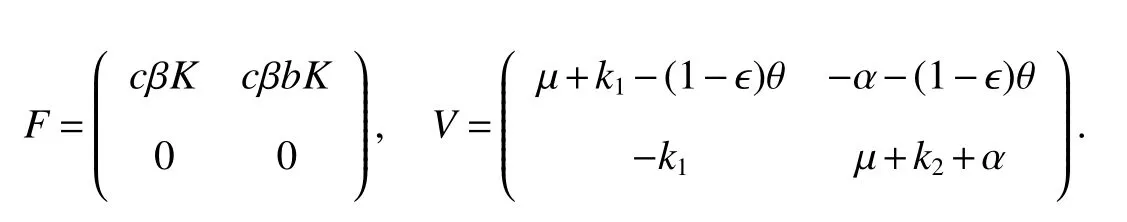
It follows that the spectral radius of matrixFV−1is

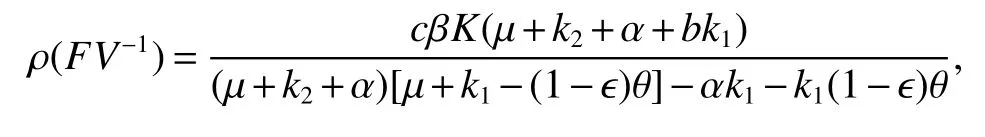
According to[14],the basic reproduction number of model(5)is

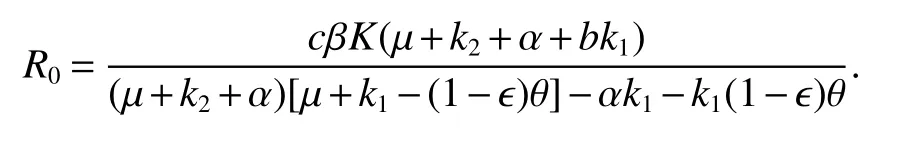
By the Theorem 2 of[14],ifR0<1,E0is locally asymptotically stable.The model(5)has the unique positive equilibriumE∗(S∗,I∗,P∗)forR0>1,where

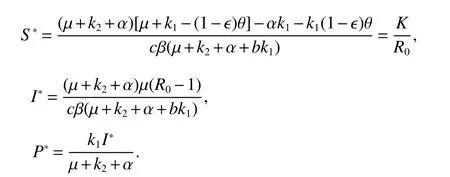
Next,we will study the local stability of the endemic equilibriumE∗.

Theorem 1IfR0>1,then the infected equilibriumE∗is locally asymptotically stable.

ProofTo prove this claim,we obtain the Jacobian matrix corresponding to system(2)aboutE∗as follows,for simplicity let

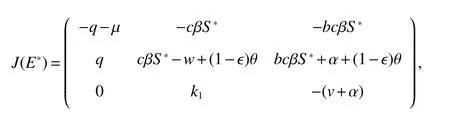
The characteristic equation of this matrix is given by

where

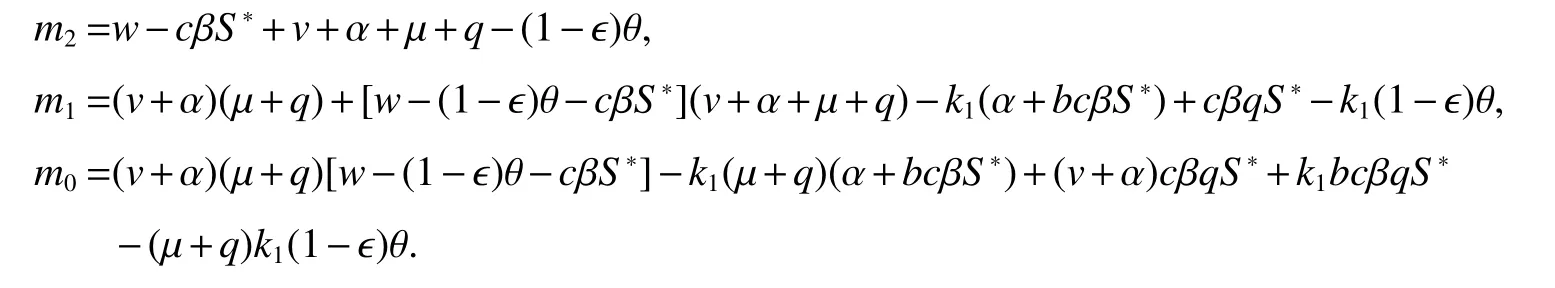
Notice that

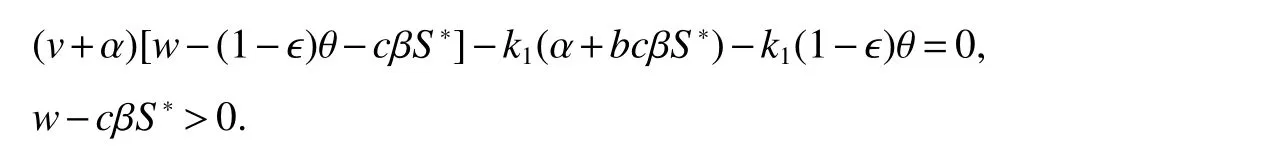
Hence

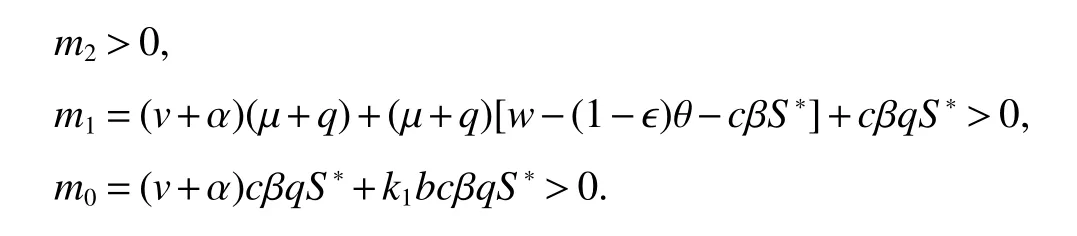
By straightforward computation,we can see thatm1m2−m0>0.By Routh-Hurwitz criteria,every root of equation(6)has negative real part.SoE∗is locally asymptotically stable whenR0>1.

We are now in a position to investigate the global stability of the disease-free equilibriumE0whenR0<1.

Theorem 2IfR0<1,then the infection free equilibriumE0is globally asymptotically stable.

ProofDefine a Lyapunov function as follows,

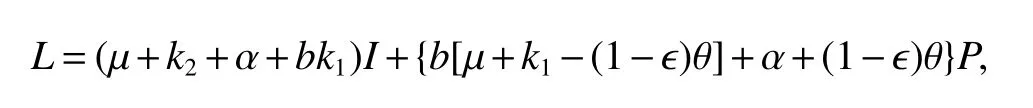
Calculating the derivative ofLalong with the solution of model(5),we have

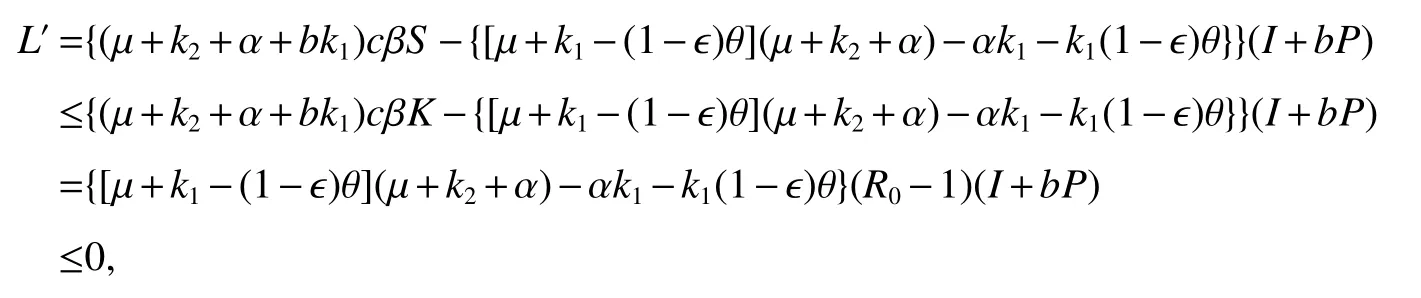
Theorem 3IfR0>1,then the infected equilibriumE∗is globally asymptotically stable.

ProofWe prove the theorem by using Lyapunov function given below.

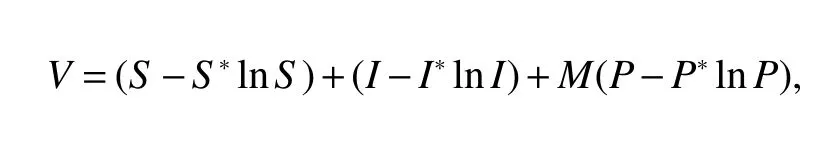
Calculating the derivative ofValong with the solution of model(5),we have

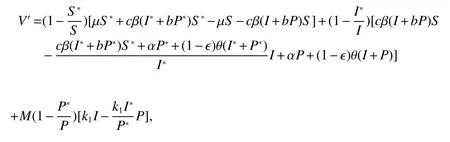
We consider the variables substitutions asThen,

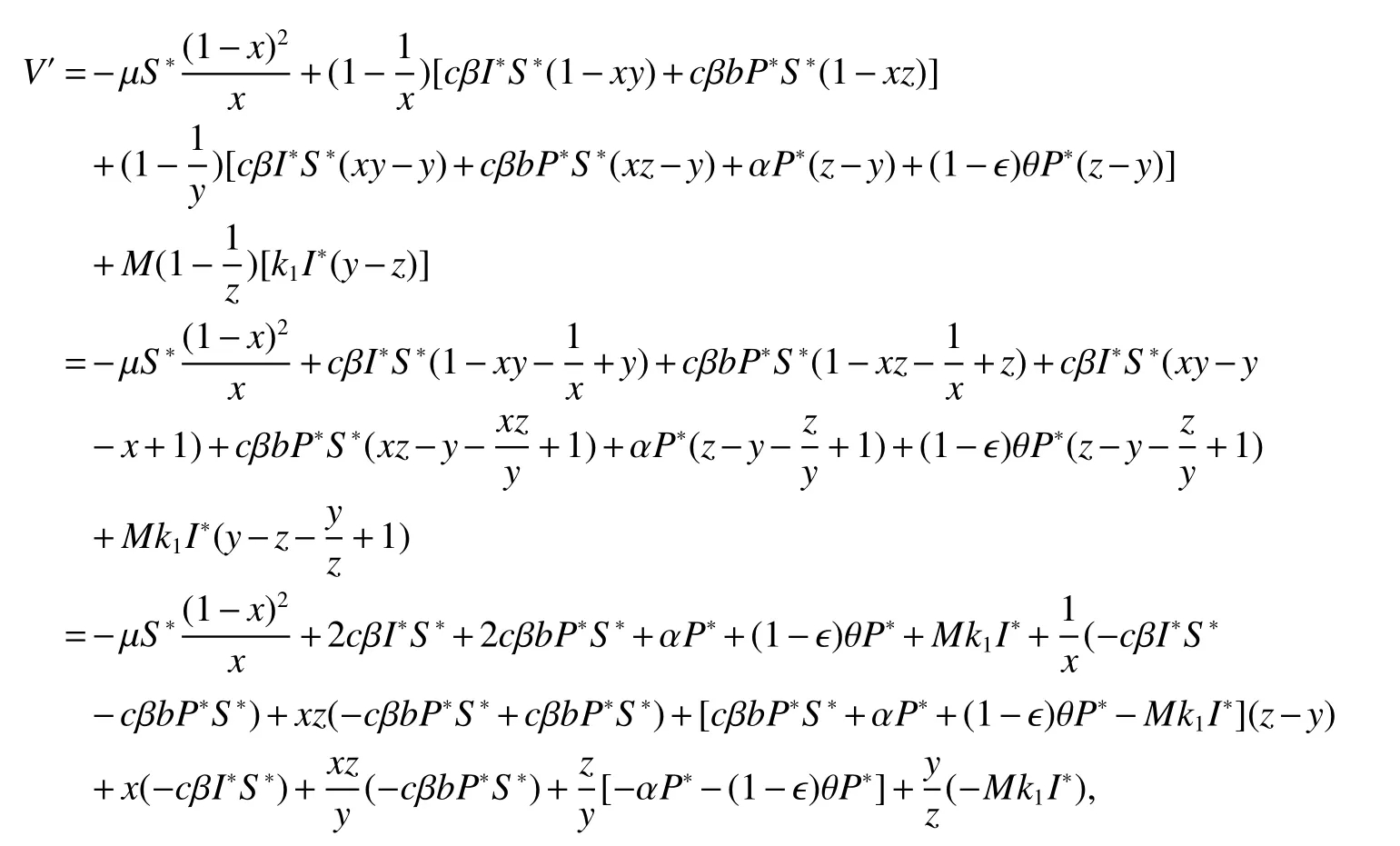
Let us choose the constantMas follows

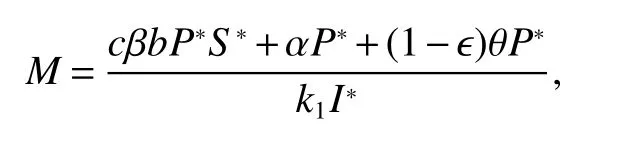
Then,

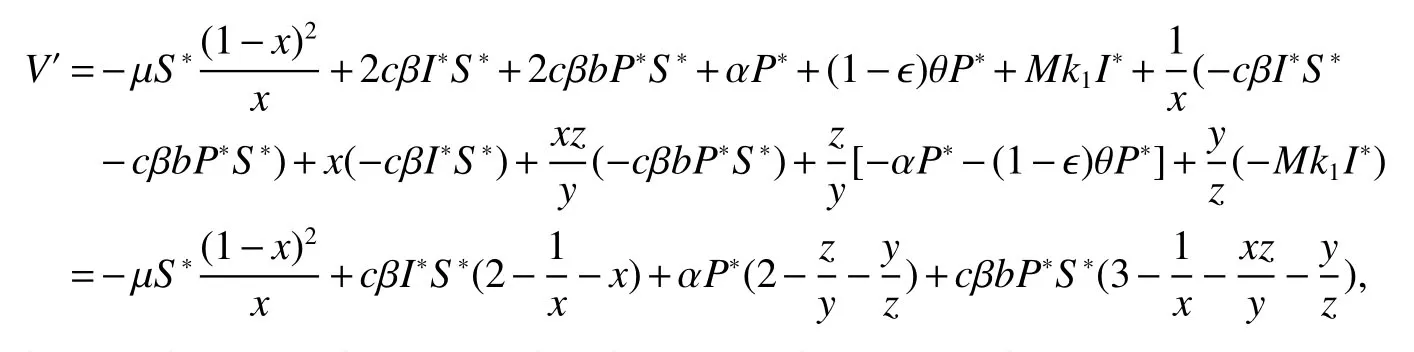
Since the arithmetic mean is greater than or equal to the geometric mean,we have

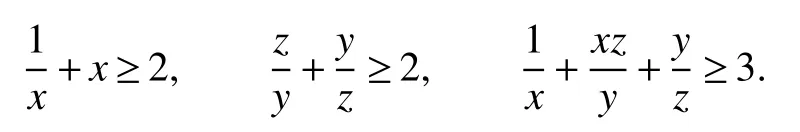
4 Discussion

In this paper,we have considered anHIV/AIDSmodel with treatment and vertical transmission under the assumption thatAIDSpatients(A)are isolated and hence are not capable of producing children that is(1 − )θA=0.Using the method given[14],we calculated the basic reproduction numberR0.Further we get the results that whenR0<1 the disease free equilibrium is globally asymptotic stable,and whenR0>1 the endemic equilibrium is globally asymptotic stable.

In[1],the basic reproduction numberR0is as follows,

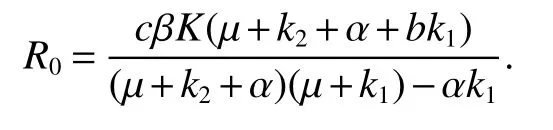
It can be easily seen that our basic reproduction number is larger than that one defined in[1].This means that adding vertical transmission of pre-AIDSpatients will increase the basic reproduction numberR0.