改进的量子蚁群算法在120急救指挥系统中应用*
董影影,张迎新
(1.西安科技大学 电气与控制工程学院,西安710054;2.福建农林大学 东方学院计算机系,福州350017)
车辆路径问题(vehicle routing problem,VRP)最早是由Dantzig和Ramser于1959年提出[1]。VRP问题在物流研究领域如减少物流运输成本,实现物流管理的科学化等方面具有很重要的现实意义。近年来对于这种强NP(Non-deterministic Polynomial)的问题研究表明,寻求其高精度解的可能性是很小的,所以利用仿生学算法如蚁群、鱼群算法来寻求其近似解是非常必要和现实的。
蚁群算法 (ant colony algorithm,简称 ACA)是由意大利学者 M.Dorigo等[2]人于20世纪90年代提出并最先应用于解决TSP(Traveling Saleman Problem)问题的。后来在TSP求解、工件排序、图着色、车辆调度以及多目标组合优化等问题中有着广泛的应用[3]。改算法有很好的鲁棒性及全局优化能力,但是基于它的收敛速度慢,易出现停滞等问题,许多学者提出了改进方法。
20世纪80年代初,Benioff和Feynman提出了量子计算的概念,众多学者因此考虑将量子计算的一些基本概念引入到经典算法上,用来改善经典算法的性能。随着Deutsch量子算法、Shor量子算法 、Grover量子搜索算法[4-6]的相继提出,量子算法(Quantum Algorithm)以其独特的计算性能受到了广泛的关注。量子蚁群算法(Quantum-inspired Ant Colony Algorithm,QACA)则将量子计算和蚁群算法相结合,把量子计算中的态矢量和量子旋转门引入到蚁群算法中,增加量子比特启发式因子,使算法的收敛速度有所提高,并有效地避免了蚁群算法易陷入局部最优的缺点。
虽然以上所研究的量子蚁群算法都有效的应用于对称性及非对称性VRP问题中,但是并没有考虑实时调度的问题,在实现最短路径的车辆调度的同时,通过使用Java语言编写了车辆实时调度的页面,仿真和实验表明,能更好的解决120急救指挥时的急救车调度问题。
1 120急救车辆调度最短路径问题
1.1 120急救问题描述
120急救车调度问题可有描述为,在接到120报警后,指挥中心从急救站派出急救车,到达报警点,因此120急救车行驶的的路径问题是特殊情况下的VRP问题,120急救车所实施的是应急事件,更注重的是时效性,因此最短路径的寻求是非常必要的。
在城市交通网络中,随着国民经济的发展,道路越来越交错复杂,因此两点间的距离正常情况下并不代表两点间的直线距离。两个地点之间存在多条路径,两地点之间的距离是指路径长度。
1.2 VRP 模型
一般地,VRP数学模型可以表示如下[3]:

N为需要经过路口的数目,i和j分别表示路口的编号,K为车辆总数,cij表示车辆由i到j的运输成本,式(1)表示成本最低的目标函数L,式(3)表示第i个路口只由第K辆车经过,式(4)表示第j个路口由第k辆车经过i后直接转移到j完成。
1.3 量子蚁群算法
量子算法是利用量子计算中的理论和概念,基于量子计算原理,使用计算机来模拟量子旋转门和态矢量表述。量子比特是量子计算中保存信息最小的单位,一个量子比特可能处于 |0>,也可能处于|1>,还可以是两种状态的线性组合,称之为叠加态。可以表示为

式(5)中,α和β为复数,代表对应状态出现的概率,0出现的概率为,1出现的概率为,α 和 β满足归一化条件:

因此,长度为n的量子位可以表示的状态多达2n个,于是,n个量子位的个体i的概率幅可以表示成

量子比特相位的改变可以由量子旋转门来实现,在传统的蚁群算法中,初始化的信息素强度相等,导致蚁群的搜索盲目性及随机性,因此信息素的更新导致寻找最优解的阻力很大。在量子蚁群算法中,用量子比特来表示信息素,用量子旋转门更新信息素。设置量子旋转门调整如下[5]:

式(8)中:[αi,βi]为第 i个量子位的概率幅,θi为第 i个量子位的旋转角度,i=1,2,…,n,θi过小,会使收敛速度减慢,θi过大,会导致算法早熟,它的方向和大小由关系式θi=Δθis(αi,βi)自动调整,Δθi为旋转角度的大小,s(αi,βi)为调整旋转角度的方向。
1.4 实验仿真及调度平台
以西安市一个医院和若干路口的实际经纬度为例,通过实验仿真,证明量子蚁群算法的有效性,并设计调度平台实时调度急救车辆。
路口及医院经纬度坐标如表1所示。
在表1中,编号1代表西安市西京医院,编号4代表首次报警点,编号5代表2次报警点。
图1为正常报警情况下的路线规划图,报警点为编号4,行车路线为1-2-3-4,首先由120报警系统的接警台受理报警电话,然后派遣急救车,此时在车载终端显示急救任务,在此页面有3个按钮为“接受任务”、“临时增加任务”、“到达目的地”3个按钮,如图2所示。
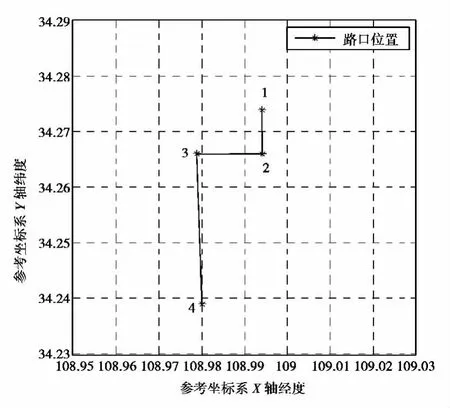
图1 首次急救任务路径规划路线

表1 路口及医院实际经纬度坐标

图2 车载终端显示急救任务
点击接受任务按钮,如图3所示,此时开始出车,根据路线规划驶向报警点,在未点击“到达目的地”按钮之前,在急救指挥中心都会显示此急救车在未到达目的地状态。
此时若接到报警离此急救车首次急救目的地不远且两个病人伤情都无紧急生命危险的情况下,可以对此急救车进行二次派发任务,派发后,车载终端“临时增加任务”按钮会变换颜色,点击此按钮,查看二次任务详情,如图4所示。
二次派发任务后,继续规划此急救车行车路径,如图5所示,行车路线为1-2-3-4-5-6-7-8。
图3 点击按钮“接受任务”显示图

图4 临时任务详情图
在急救车到达目的地,即编号为5的地点时,点击“到达目的地”按钮,如图6所示并按路径规划回到医院,完成急救任务。
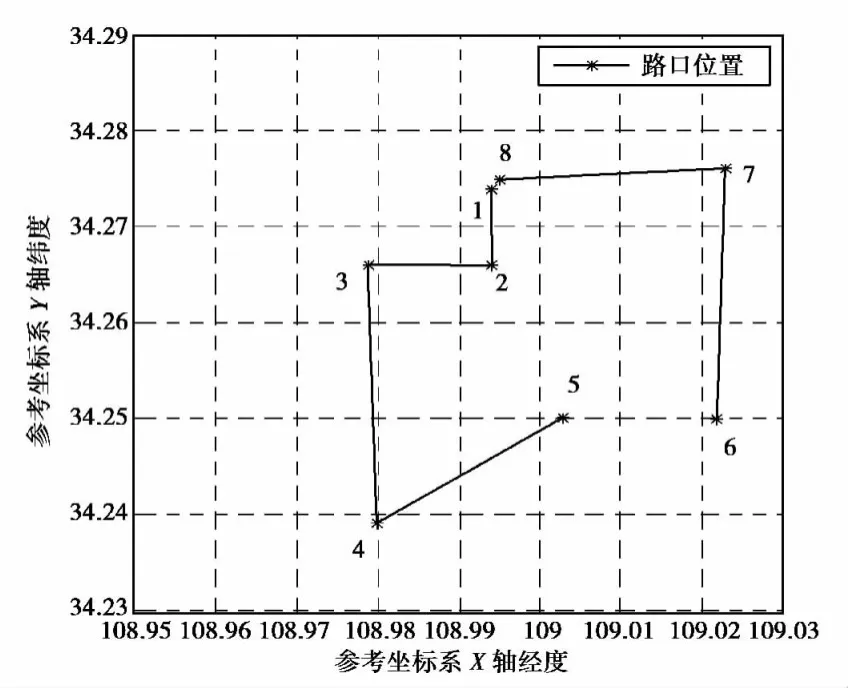
图5 增加临时任务路线图
图6 到达目的地详情
2 结语
基于120急救任务的特殊性,通过在蚁群算法中加入量子比特和量子旋转门的量子蚁群算法对急救任务中的路口进行最短路径的寻找,并在急救过程中对特殊情况下的急救车进行二次急救任务的派发,更大程度的保障了伤者的救治,同时使用Java语言和SQL数据库编写急救过程中的动态调度系统,实时监控车辆的行驶状态,是120急救的一个新的可行手段。
[1]马良,朱刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008
[2]DANTIZIG G,RAMSER J.The Truck Dispatching Problem[J].Management Science,1959,6(1):80-91
[3]DORIGO M,MANIEZZO V,COLORNI A.Ant System:Optimization by a Colony of Cooperating Agents[J].IEEE Transactions on System,Man and Cybernetics,1996,26(1):29-41
[4]杨佳,许强,张金荣,等.一种新的量子蚁群优化算法[J].中山大学学报:自然科学版,2009,48(3):22-27
[5]李跃光,赵俊生,张远平.求解TSP的改进量子蚁群算法[J].计算机工程与设计,2009,30(16):3843-3845
[6]戴芬,刘希玉,王晓敏.基于量子计算技术的蚁群算法的研究与应用[J].计算机应用技术,2009(6):99-102
[7]王越,叶秋冬.蚁群算法在求最短路径问题上的改进策略[J].计算机工程与应用,2012,48(11):35-38
[8]DEUTSEH D.Quantum Computational Networks[J].Proc Roy Soc London,1988(25):73-90
[9]SHOR P W.Algorithms for Quantum Computation[J].IEEE Computer Society Press,1994(11):124-134.
[10]GROVER L K.A Fast Quantum Mechanics Algorithm for Database Search[M].New York:USA ACM Press,1996

