Dynamics of Population Model with Aggregate Intermittent Dispersal∗
ZHU Tie-Lei,JIANG Bing-Yu,ZHANG Jie,WANG Peng-fei,ZHANG Long
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: In this paper,we propose a new aggregate dispersal population model.The migration behavior modelled in this paper is in the form of intermittence,which is different from both continuous dispersal or impulsive dispersal,instead,it is synthesis of these types.Some criteria for the permanence,extinction of system,existence,uniqueness and global stability of positive periodic solution are established by utilizing analytic method based on discrete dynamical systems.Besides,results are further confirmed by numerical simulations.
Key words:Intermittent dispersal;Permanence;Periodic solution;Global stability
0 Introduction
Generally speaking,organisms’residences are fixed within their life-cycle.However,due to the changes of external environment,or the quantity change of populations themselves,some organisms tend to leave their current habitats and migrate to another ones.Therefore,migration(or dispersal)is a ubiquitous and fundamental biological process for organisms,which study usually includes ecology,evolutionary biology,microbiology,molecular biology,mathematics etc.[1].During the last couple of decades,a great number of mathematical models have been proposed to characterize and investigate the dynamics of dispersal population(e.g.,[2,3]).The most important results for the preceding models are persistence,extinction,stability analysis of equilibriums or periodic solutions etc.(e.g.,[1,3–5]).
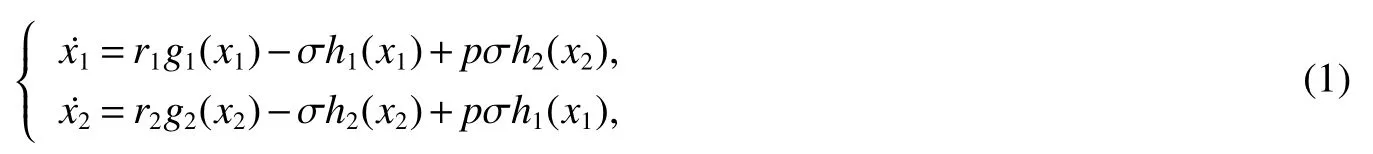
As early as 1960s’,single-species continuous dispersal model have been extensively investigated,and many important results and monographs had been obtained(e.g.,[1,3,5]).Freedman and Waltman[6]proposed the following two patches continuous dispersal model:gi(xi)is the specific growth rate ofxi,hi(xi)is the migration function,i=1,2.They discussed existence of positive equilibrium and its global asymptotic stability.The dispersal behavior in(1)occurs all the time and bidirectionally,i.e.,it’s continuous bidirectional model.Besides,Hasting[5]considered that a population will be stable if dispersal is high enough.Teng and Lu[7]studied the effect of dispersal on persistence and extinction.Lu and Takeuchi[4]discussed the global asymptotic behavior of single-species discrete diffusion system.With the impulsive differential equations introduced into population dynamics[8],many significant findings(e.g.,[9–11])have been obtained by ecologists,biologists and bio-mathematicians.
Zhang[12]proposed the following single-species logistic model with impulsive unidirectional dispersal between two patches:
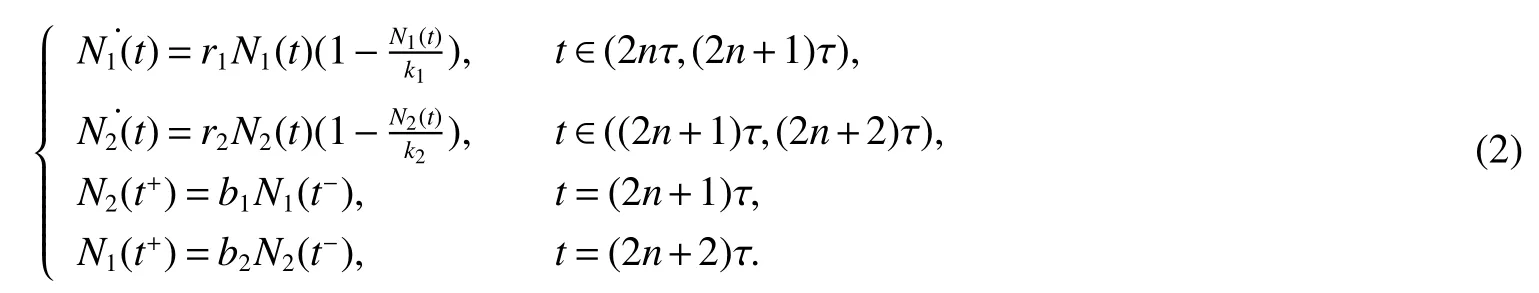
The populationN=(N1,N2)inhabits two patches(patch 1 and patch 2)and alternate periodically;Ni(i=1,2)is the density of species in thei-th patch.Intrinsic growth rate of population in thei-th habitat is denoted byri(i=1,2);ki(i=1,2)denotes the carrying capacity in thei-th patch;0≤bi≤1(i=1,2),is the dispersal rate from thei-th patch toj-patch(ij).presents the density of the population in thei-th patch before the(2n+i)-th pulse dispersal at timet=(2n+i)τ (i=1,2).present the density of the population in thei-th patch after the(2n+i)-th the pulse dispersal at timet=(2n+i)τ(i=1,2).Criteria on permanence,extinction,existence,global stability for periodic solution were established by theory of discrete dynamic system.
Actually,the movement of dispersal can be divided into two types,i.e.,continuous(e.g.,[1,5])and discontinuous(e.g.,[11,15]).For the continuous case,authors always assumed that it occurs all the time.For the latter case,authors always assumed it occurs in the form of impulse.However,it is often the case that dispersal movement spends some time periods for species to migrate from current patch to a new one.In this case,the dispersal behavior occurs intermittently,neither continuously nor impulsively,but their integration.There are some reasons for this.
First,environmental condition(weather,landscape)may not allow organisms to finish migration in short time.For example,salmons can make amazing journeys,sometimes moving hundreds of miles upstream against strong currents and rapids to reproduce.The river’s direction is opposite to that of salmons’ migration,which hampers salmons migration process,as a result,people sometimes have to clean the barriers which are lethal to fish.
Second,another reason is the habitual nature of migratory species.For example,the Serengeti plains and the Ngorongoro Conservation areas in northern Tanzania are home of giant herds of wildebeest in every year’s December to March.Whereafter,from the end of every April to late July,wildebeests migrate from Tanzania’s Serengeti Plains to Kenya’s Masai Mara National Reserve.Soon after,from every September to November,they live in Kenya’s Masai Mara National Reserve.Then,from November to December,they come back to Tanzania’s Serengeti Plains,and then they repeat the journey alternately.Besides,in autumn,it may be disadvantageous for some species to rapidly pass areas with abundant food,if they can not be sure of finding similar plentiful supplies in other patches[16].
A major loss accompanied with migration is mortality because there almost exists different dangers or enemies for migratory species during migration.On the other hand,migratory species must travel through unfamiliar areas,and often go through alien habitat[16].For example,wildebeests congregate and form much larger herds before crossing Mara River.However,crocodiles hide themselves in water,and wait for any feeble wildbeests that can not cope with the strong currents or lose their mothers as the herds cross.Moreover,in terms of many species,migration and breeding is mutually exclusive,which means that animals can not breed during migration.Therefore,we should take the mortality cost of migration into account.
Obviously,the preceding movement process of migratory species is unidirectional,meanwhile,it occurs intermittently.Based on above considerations,we proposed a single species model with logistic growth and intermittent unidirectional dispersal as follows:

We suppose that the whole life-cycle of migratory populationN=(N1,N2,N3,N4)is composed of two inhibiting process,i.e.,N1,N3,and two aggregate migration process,i.e.,N2,N4,and alternates periodically.During the time interval(nτ,nτ+τ1),the populationN1inhabits in patch 1,and does not dispersal.When timet→nτ+τ1,it starts to migrate,as a whole,with the success rate ofb1to the patch 2.The time interval(nτ+τ1,nτ+τ1+τ2)presents the migratory process of populationN2from patch 1 to patch 2.Ast→nτ+τ1+τ2,it arrives at patch 2 with the success rate ofb2.From that point,the populationN3stays on patch 2 during the time interval(nτ+τ1+τ2,nτ+τ1+τ2+τ3).Then,as timet→nτ+τ1+τ2+τ3,it leaves patch 2 and starts to migrate from patch 2 to patch 1 with the success rate ofb3.The time interval(nτ+τ1+τ2+τ3,(n+1)τ)represents the dispersal process of populationN4from patch 2 to patch 1.As timet→ (n+1)τ,it comes back to patch 1 with the success rate ofb4.=presents the density of the population in thei-th procedure before the(n+i)τ-th pulse dispersal at timepresents the density of the population in thei-th procedure after thenτ-th pulse dispersal at time
The organization of this paper is as follows.In section 1,we establish the stroboscopic map of system(3),and introduce some assumption and lemma.In Section 2,criteria on the permanence and extinction for this system are established.Besides,the existence and uniqueness of positive periodic solutions for the models are obtained.What’s more,the global stability of positive periodic solutions is presented.Finally,the numerical simulations and discussion are presented to illustrate our results.
1 Preliminaries
Before going into details,we first draw a clear definition of permanence.The definitions of permanence or persistence are numerous,but here we refer to[2,14,17].
Definition 1Systems(3)are said to be permanent,if there are positive constantsmiandMisuch that

for any positive solutionsN(t)=(N1(t),N2(t),N3(t),N4(t))of system(3).
Next,to study the permanence,existence and uniqueness of positively periodic solutions for system(3),we takewhich on substituting into(3)becomes
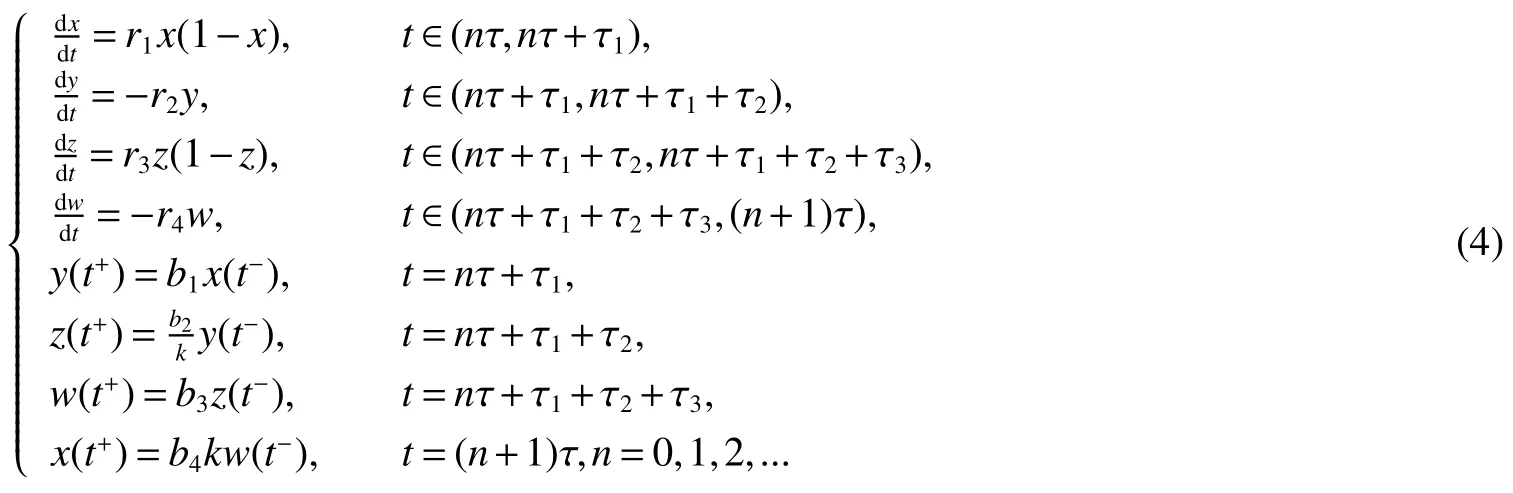
By integrating and solving the first four equations of(4),we get
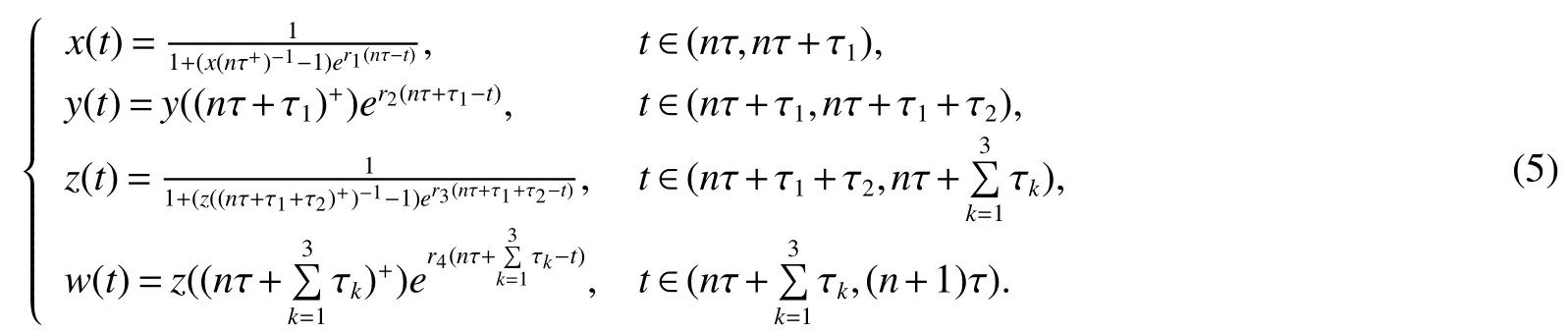
Similarly,considering the last four equations of system(4),we obtain the following stroboscopic maps
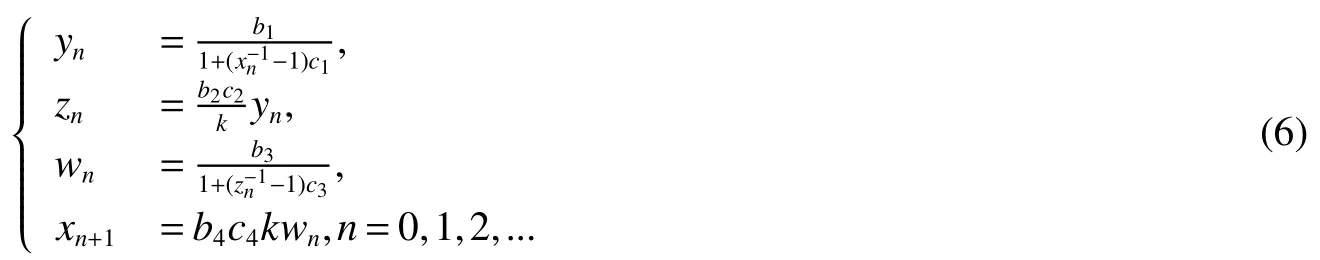
whereyn=y((nτ+τ1)+),zn=z((nτ+τ1+τ2)+),wn=w((nτ+τ1+τ2+τ3)+),xn+1=x((n+1)τ+),0
Lastly,to establish the global stability of positively periodic solutions,we introduce the following well known result of discrete dynamical system theory:
Lemma 1[13]Letbe continuous,and supposeDF(0)exists with=DF(0).In addition,assume
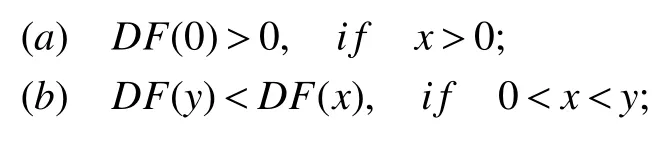
IfF(0)=0,let λ=ρ(DF(0)).If λ<1,then for everyx≥0,F(n)(x)→0 asn→∞;if λ>1,then eitherF(n)(x)→∞asn→∞for everyx>0 or there exists a unique nonzero fixed point q of F.In the latter case,q>0 and for everyx>0,F(n)(x)→qasn→∞.
IfF(0)0,then eitherF(n)(x)→∞asn→∞for everyx≥0or there exists a unique fixed point q of F.In the latter case,q>0 and for everyx>0,F(n)(x)→qasn→∞.
2 Main results
First,we establish sufficient and necessary conditions to ensure that system(3)is permanent(or extinct).
Theorem 1Assume that1 or(≤ 1),then system(3)is permanent(or extinct).
ProofFirst,we prove if1,then system(3)is permanent.Since 0 ≤bi≤ 1 and 0 ≤ci=e−riτi≤ 1i=1,2,3,4,from system(3)we have

Next,in system(4),we have
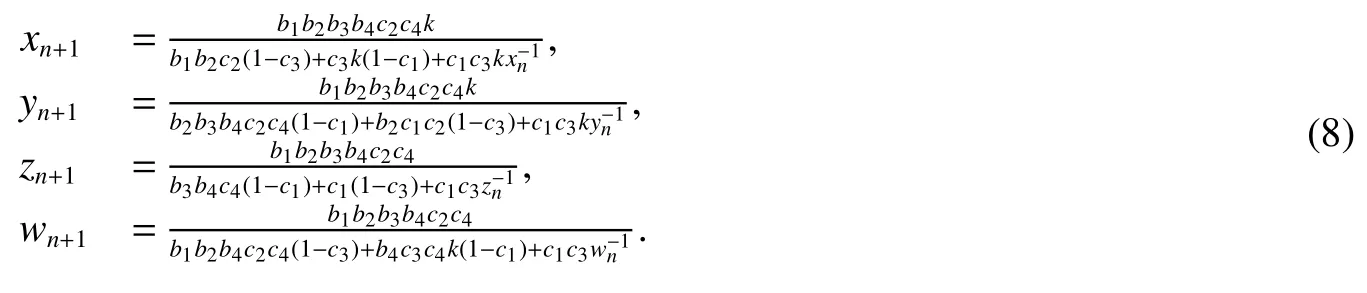
Let
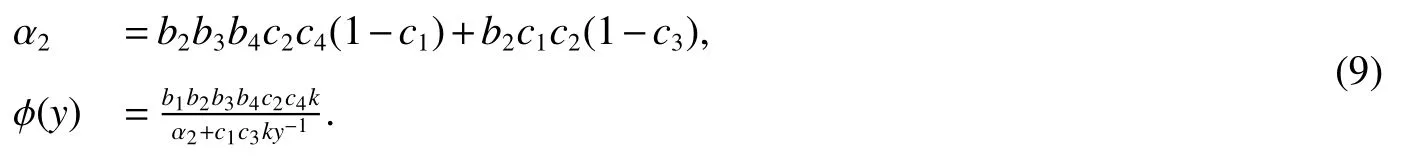
From(7)we see that the sequence{yn}is bounded above and then we have

If there existsNsuch thatyN+1≤yN.Thenyn+1≤ynfor all

Diving(11)byc1c3k,we have


Then,we have

Similarly,we can conclude
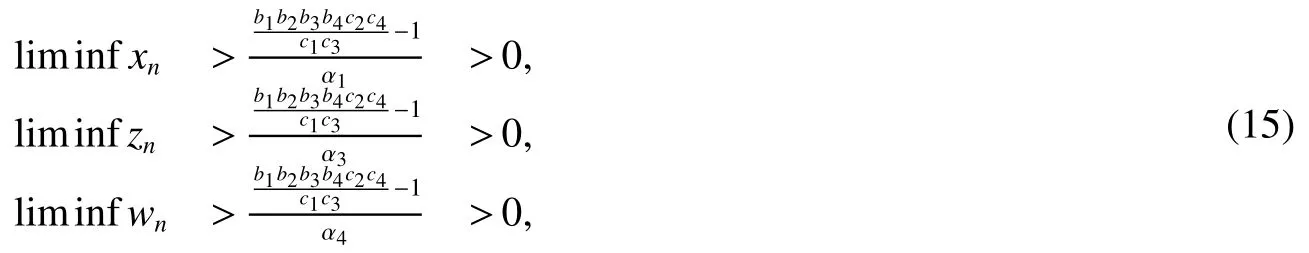
where α1=b1b2c2(1−c3)+c3k(1−c1),α3=b3b4c4(1−c1)+c1(1−c3),α4=b1b2b4c2c4(1−c3)+b4c3c4k(1−c1).Based on above arguments,we can see system(3)is permanent.

Therefore,the sequence{yn}is non-increasing.Let the limit of{yn}is γ,then γ ≥ 0.Take limit for two sides of(16),we can obtain

Therefore γ=0,i.e.limyn=0
Similarly,by the same arguments like above,we can conclude limxn=0,limzn=0,limwn=0.Therefore,if≤ 1,the system(3)is extinct.The proof is complete.
Remark 1We can see that the assumption1 in Theorem 1 is very simple and easy to verify,which means that a higher successful migratory ratebi,i=1,2,3,4,a higher growth rateri(i=1,3)and a longer migration period(that is,enough time to be restored,mature,breed,etc.)will greatly enhance the survival of natural populations.Furthermore,we can easily conclude thatK=is a threshold value of persistence for above system(3),i.e.ifK>1 it will be permanent,ifK≤1 it will be extinct.
Further,we will prove there is a unique positive periodic solution for system(3)by proving the existence and uniqueness of the fixed points of system(8).
Theorem 2There is a unique fixed point(ξ1,ξ2,ξ3,ξ4)for system(8)if
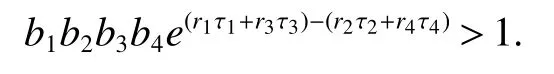
ProofLet(ξ1,ξ2,ξ3,ξ4)is the fixed point of system(8),we have
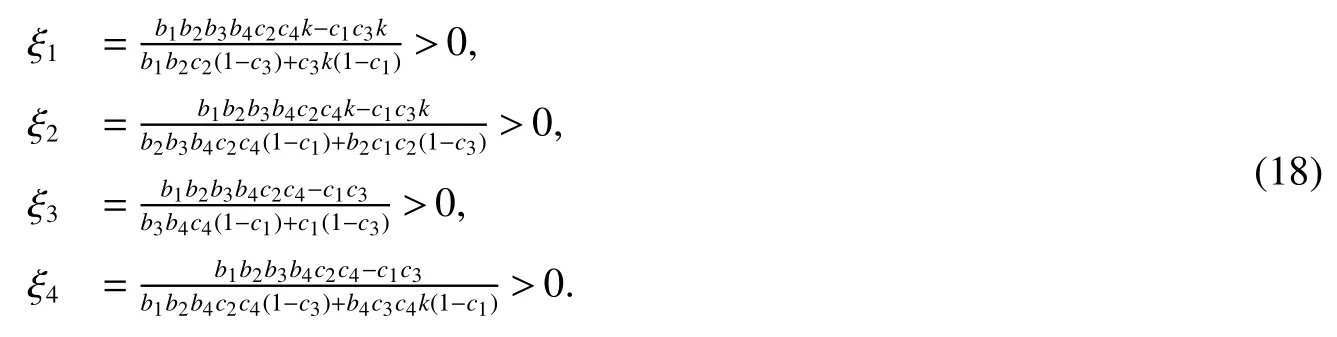
Therefore,there exists a unique positive fixed point(ξ1,ξ2,ξ3,ξ4)for system(8).This completes the proof.
Theorem 3If>1,then for every(x,y,z,w)>(0,0,0,0),F(n)(x,y,z,w) → (ξ1,ξ2,ξ3,ξ4)asn→∞.
ProofCorresponding to(6),let us consider the following system
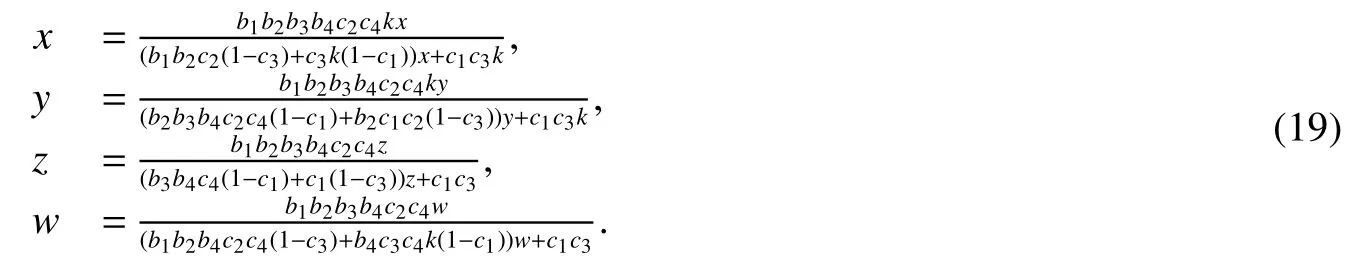
From above system,we have that

Obviously,F(y)∈C1in int(R+)andF(0)=0.Then we have
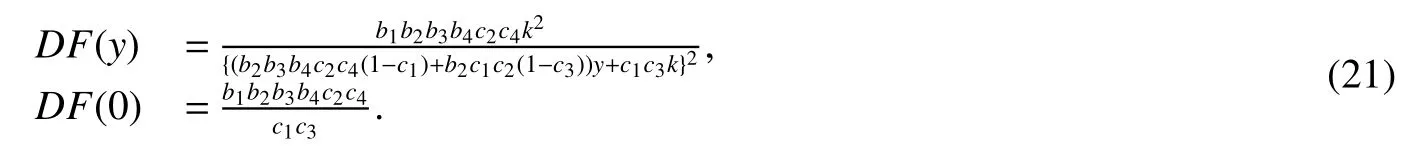

Remark 2In this paper,we consider intermittent dispersal model between two patches,comparing the model(3)with(2),we find that system(2)is the special case for system(3).In fact,if τ2=0 and τ4= τ −(τ1+τ2+τ3)=0,we can see system(3)degenerate into(2),i.e.,the behavior of dispersal occurs instantaneously at the impulsive time.Therefore,we can conclude that system(3)can be a better choice to characterize the real aggregate migration behavior.
Remark 3In this paper,we only discuss the single species with unidirectional intermittent dispersal between two patches.However,in the real ecosystems,migration populations usually choose many patches more than two as their habitats.Therefore,there is a very important open question is that whether the above results are still true for the single species model with unidirectional intermittent dispersal between n patches.
3 Numerical simulations and Discussion
In order to validate our theoretical results for system(3),we do some numerical simulations by using the following parameters:
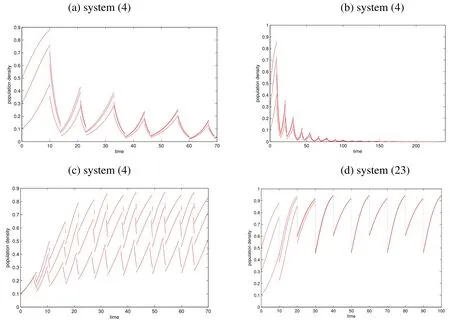
Fig 1 Dynamical behaviors of system(4)and system(23)

Table 1 Simulations of model(4)
Here SS:system state,PS:permanent and stable,EU:extinct and unstable,k=1.
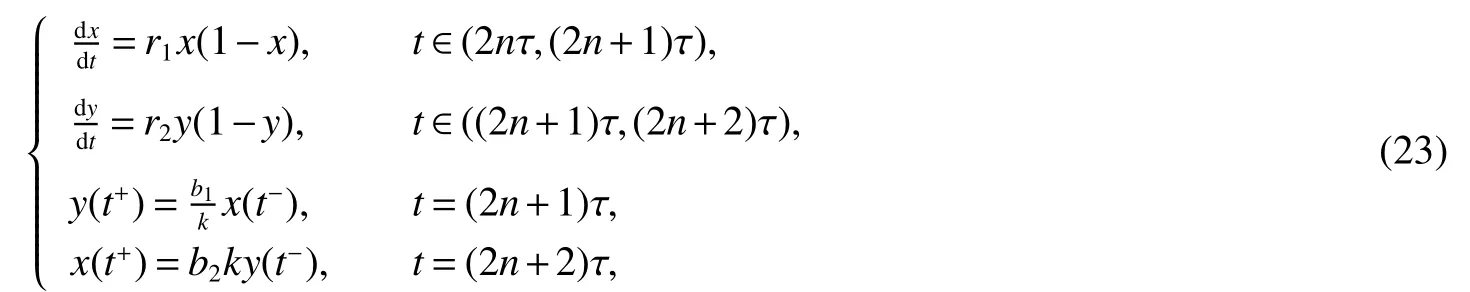
In table 1,we take τ =10.8 in case 7-9,and τ =23 in other cases.For case 1,we can easily obtain λ =1.08>1.Similarly,we can obtain that λ ≤ 1 is true for cases 4-6 and case 11,and λ >1 in other cases.According to the theorem 1,2 and 3,we can conclude that system(4)is permanent(or extinction),existence and global stability of positive periodic solution.According to the figure 1.c,we see that the result is similar to the result of impulsive dispersal when migration time is short enough.From the figure 2.a,we can see that population density in the system(23)varies at high level while system(4)varies at low level,although they are both persistent and stable.According to the figure 2.b,system(23)is permanent and system(4)is extinct in similar conditions.Therefore,we can conclude that there exists evident different dynamics between impulsive dispersal and intermittent dispersal.The intermittent dispersal is more realistic than impulsive dispersal.
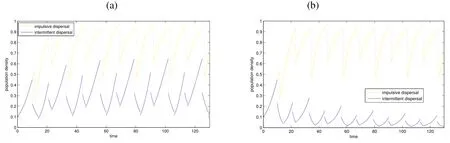
Fig 2 Comparison of system(23)and(4)
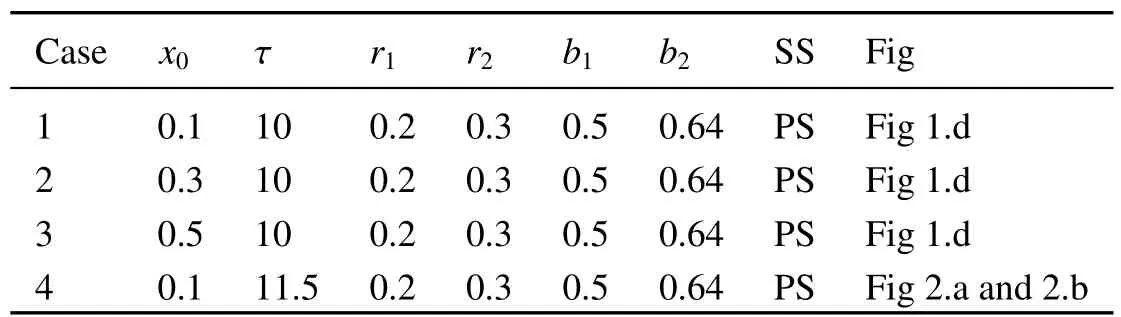
Table 2 Simulations of model(23)
Here SS:system state,PS:permanent and stable,EU:extinct and unstable,k=1.
In a word,comparing our results with the results of continuous and impulse dispersal models,we conclude that intermittent dispersal model encompass more situation and dynamical properties that can not be characterized either in continuous dispersal model or impulsive dispersal model.Therefore,hybrid model with intermittent dispersal model maybe a better choice to read the real ecosystems.

