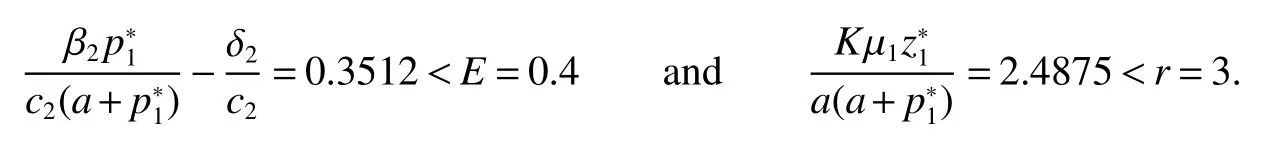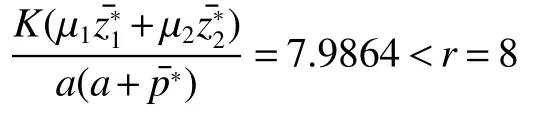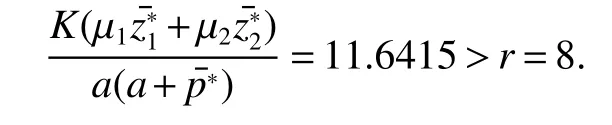Global Stability in a Zooplankton-phytoplankton Model∗
ZHANG Zhen-zhen,Mehbuba Rehim
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: In this paper,we describe a two-zooplankton one-phytoplankton system that exhibits a Holling type II functional response for the grazing of phytoplankton by zooplankton.Combined effort(E)is used to harvest the population.We consider the impact of harvesting on the coexistence of competitive predators.We firstly consider the positivity and boundedness of the solution and existence of equilibria.Secondly,stability criteria of the model is analyzed both from local and global point of view.Theoretical results of this paper justified with numerical simulations.
Key words:Existence;Coexistence;Harvesting;Stability
0 Introduction
In marine ecology,almost all aquatic life is based upon plankton,which are the most abundant form of life floating freely near the surfaces of all aquatic environments[1,2].Plankton are made up of phytoplankton and zooplankton.Phytoplankton are primary producers.As the base of the oceanic food web,they use chlorophyll to convert energy,inorganic chemicals,and dissolved carbon dioxide gas into carbohydrates.Zooplankton are microscopic animals that eat other plankton and serve as a most favorable food source for fish and other aquatic animals.As we know,phytoplankton are not only the basis for all aquatic food chains,they render very useful service by producing a huge amount of oxygen for human and other living animals after absorbing carbon dioxide from surrounding environments[3].
Recently,several mathematical models have been generated of plankton systems[4−12].For example,a simple nutrient-phytoplankton model was used to explore the dynamics of phytoplankton blooms by Huppert et al[5],Pei et al[6]considered the impact of harvesting on the coexistence and competitive exclusion of competitive predator.They proposed and investigated a two-zooplankton one-phytoplankton model with harvesting.In[7],authors have dealt with a two-zooplankton one-phytoplankton system in the presence of toxicity.In[8],considering that some phytoplankton and zooplankton are harvested for food,a phytoplankton-zooplankton model with harvesting is proposed and investigated.Zhang and Wang[12]considered a nutrient-phytoplankton-zooplankton model in an aquatic environment and they studied the global dynamics of the system.
In this paper,we consider a two-zooplankton one-phytoplankton system with a Holling typeIIfunctional response.
The basic model is governed by the following ordinary differential equations:
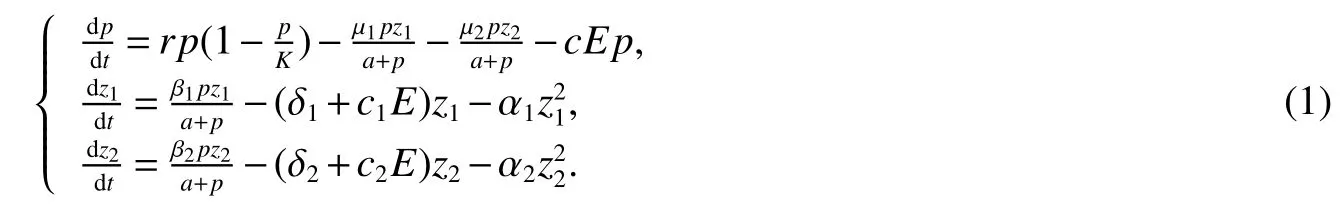
with initial conditions
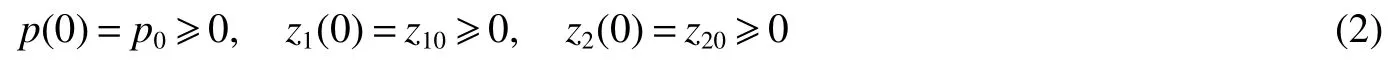
Wherep,z1andz2are the sizes of the phytoplankton population and the two different zooplankton populations,respectively,at time t.In the absence of zooplankton,the growth of the phytoplankton population is logistic with an intrinsic growth raterand carrying capacityK,or the maximum number of individuals that the environment can support.It is considered that the phytoplankton population is consumed the two different zooplankton populations and it is recycled into the two different zooplankton system.The two different zooplankton populations consume the phytoplankton population with functional responses of the formsµipzi/(a+p),thereby contributing to their respective growth with βipzi/(a+p)(satisfying the obvious restriction 0< βi< µi).The parameterais half saturation constant for a Holling typeIIfunctional response[13]and δiis the natural death rate for zooplankton species i.We consider the density-dependent mortality rate of the zooplankton aswhich describes either a self-limitation of the consumer or the influence of predation,where αidenotes the intraspecific competition coefficients of zooplanktoni.Self-limitation can occur if there is some other factor(other than food)which becomes limiting at high population densities.Predation on a consumer can increase asif higher consumer densities attract more attention from predators or if consumers become more vulnerable at higher densities[14].The constantsc,c1andc2are the catch ability coefficients(or harvest rates)of the three species respectively.The constant E is the harvesting effort(i=1,2).
The remainder of this paper is organized as following.In the next section,firstly,we prove the positivity and boundedness of the solutions of system(1),and then analyze the existence of the interior equilibrium.In section 3,we analyze the stability of the equilibria both from a local and global point of view for the model.Some numerical simulations are performed to illustrate the main analytical results in section 4.
1 Positivity and boundedness of the solution and existence of equilibria
Regarding the positivity and boundedness of the solution for the system(1)we state the following theorem.
Theorem 1All the solutions of system(1)with the positive initial conditions are positive and uniformly b ounded within a regionwhere
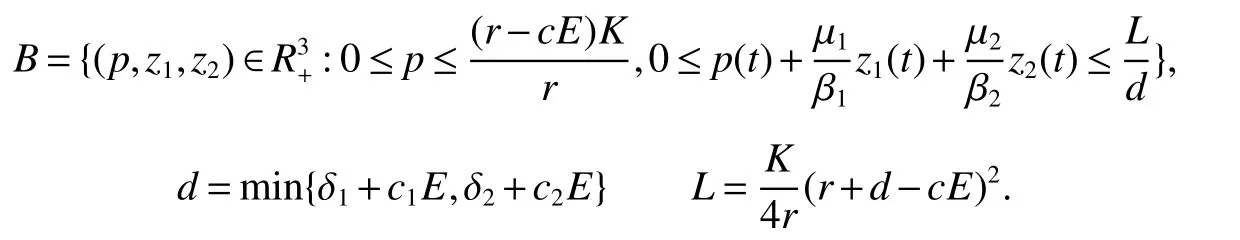
ProofThe positive of the solution is easy,we omit it here.From the first equation of equations in system(1),we get
Let us consider the functionDerivative ofVwith respect to(1),we obtain
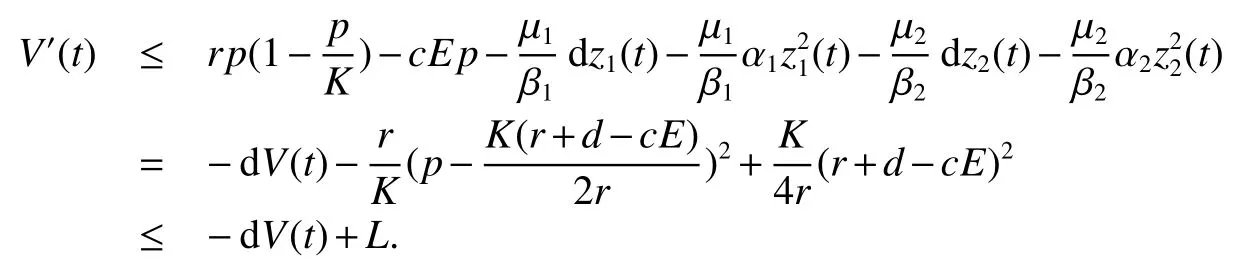
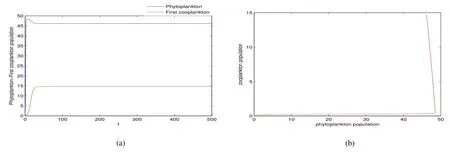
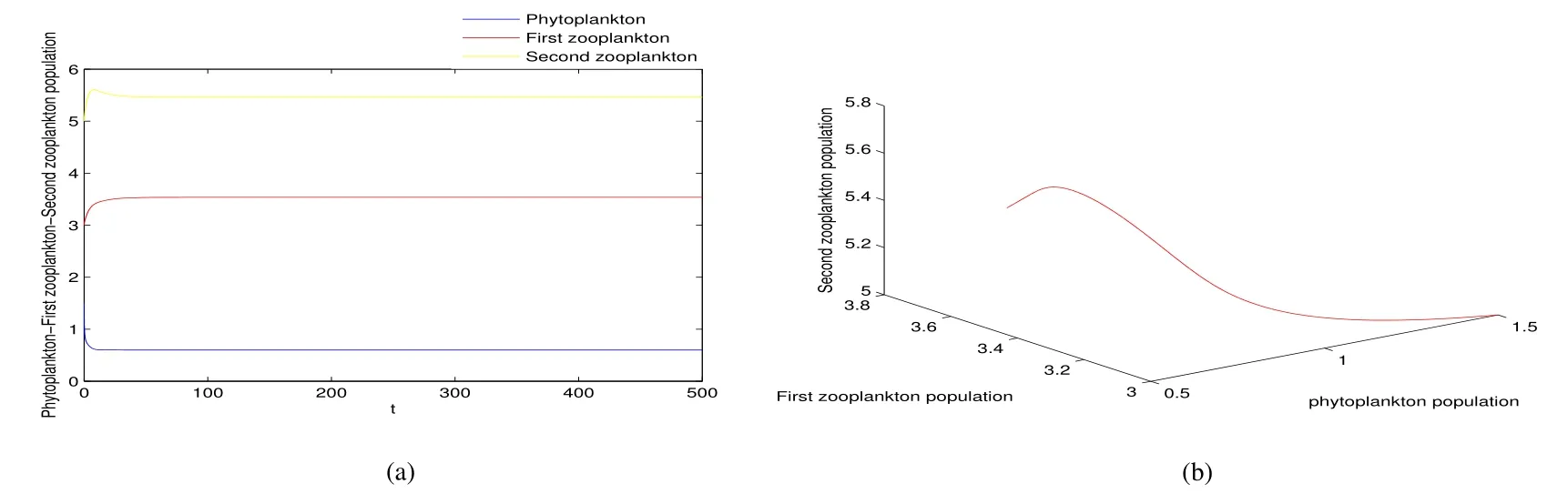
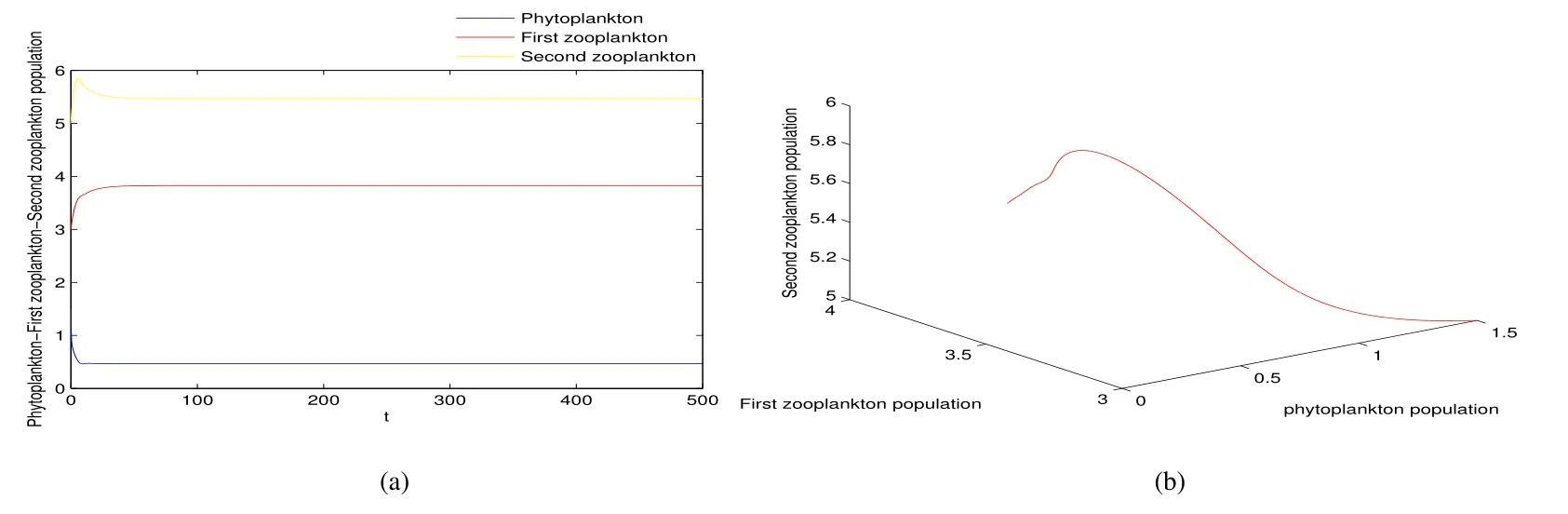
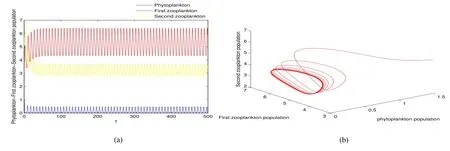
Thus ast→ +∞,0 System(1)possesses five possible nonnegative equilibria,namely the extinction equilibriumE0(0,0,0)and the zooplankton-free equilibriumand the zooplankton second-free equilibriumand the zooplankton first-free equilibriumand the coexistence equilibrium For the zooplankton-free equilibriumif such exists,it must satisfy the following equation: So,ifr−cE>0,thenexists and For the zooplankton second-free equilibriumand the zooplankton first-free equilibriumif such exist,they must satisfy the following equation: From this we have subject to Let Then intercepts of the functionh(p)andg(p)can provide us the information on the number of the zooplankton secondfree equilibrium or the zooplankton first-free equilibrium of System(1).We have that (1)Ifp0>0,then we have<0 forp∈ (p0,∞).Further,ifp0>0,thenandh()=0.Hence,h(p0)>0 andp0 (2)Ifp0<0,then for allt∈(0,+∞),Further,ifµi(δi+ciE)>αia(cE−r),then(5)has exactly one positive real root(Fig.1 b,c);ifµi(δi+ciE)< αia(cE−r),then there is no any intercept ofh(p)andg(p)in the first quadrant(Fig.1 d). Fig 1 The graph of function h(p)−g(p)=0 For the coexistence equilibriumif such exists,it must satisfy the following equation: It follows from the first of equation(6)thatFrom the second and third of equation(6),the componentsof equilibriumE∗are both positive providedwheresatisfies the equation Accordingly,if the derivative off(p)is always negative forp∈(p11,p12),then the uniqueness of the coexistence equilibriumE∗can be obtained.It seems that checking the condition for the quintic equationf(p)is more difficult.We summarize the existence results of equilibria as follows. Theorem 2If the inequalities(4)hold andr−cE>0,then system(1)possesses unique equilibriumandi=1,2.If the inequalities(8)hold,then coexistence equilibriumexists.Where For the purpose of avoiding that the total population of the system(1)declines to zero as time goes to infinity,we first investigate the behavior of the extinction equilibrium in the following.It is easy to check that the system(1)possesses the biological feasible equilibria for any parametric value. Theorem 3Ifthen the extinction equilibriumE0(0,0,0)is globally asymptotically stable andE0(0,0,0)is unstable if ProofThe eigenvalues of the characteristic equation aboutE0(0,0,0)are λ1=r−cE,λ2= −δ1−c1E,λ3= −δ2−c2E.then the extinction equilibriumE0(0,0,0)is locally asymptotically stable andE0(0,0,0)is unstable if Sincep(t),z1(t)andz2(t)are positive,it follows from=0 if and only if(p,z1,z2)=(0,0,0). ThusE0is globally asymptotically stable by Lyapunov-LaSalle invariance principle.The proof is completed. Theorem 4Suppose that zooplankton-free equilibriumexists.Ifthen zooplankton-free equilibriumis globally asymptotically stable andis unstable if ProofThe characteristic equation atis given by It is clear that equation(9)has negative root λ1then Calculating the derivative ofV0along the positive solution of system(1),we have Theorem 5then the zooplankton second-free equilibriumis globally asymptotically stable. ProofThe characteristic equation aboutis given by So, λ2<0 and λ3<0.This shows that all roots of equation(11)have the negative real part.The zooplankton second-free equilibriumis locally asymptotically stable.Further,let us define Lyapunov functional as Calculating the derivative ofV1along the positive solution of system(1),we have By using similar way we can prove the following Theorem Theorem 6Ifthen the zooplankton second-free equilibriumis globally asymptotically stable. Theorem 7Ifthen the coexistence equilibriumis locally asymptotically stable,andis unstable if ProofThe characteristic equation aboutis given by where Calculating the derivative ofV3along the positive solution of system(1),it follows that In this section,in order to facilitate the interpretation of our mathematical results,we present some numerical results for some particular values of the parameters associated with the model system(1). (1)Letr=3,K=50,µ1=0.5,µ2=0.5,a=3,β1=0.4,β2=0.4,δ1=0.002,δ2=0.2,α1=0.02,α2=0.2,c=0.2,c1=0.2,c2=0.5,E=0.4.It is easy to verify that Then the conditions of Theorem 5 are satisfied.Hence the equilibriumE1(46.1792,14.6800,0)is globally asymptotically stable,which is shown in Fig.2. Fig 2 Solution of the(1)showing E1(46.1792,14.6800,0)is stable.The initial value is(0.8,0.2,0.45) (2)Consider the following choice of parametric values:r=8,K=1.6,µ1=1.1,µ2=0.75,a=1,β1=0.25,β2=0.35,δ1=0.003,δ2=0.002,α1=0.02,α2=0.02,c=0.1,c1=0.2,c2=0.2,E=0.1.It is easy to compute that So,the condition of Theorem7 holds,then the interior equilibriumE∗(0.5997,3.5360,5.4604)is globally asymptotically stable,which is shown in Fig.3.In absence of harvesting effort(E=0),the globally asymptotically stable equilibriumE∗exists at(0.4667,3.8273,5.4682)in Fig.4. Fig 3 Solution of the(1)showing E∗(0.5997,3.5360,5.4604)is stable.The initial value is(1.5,3,5) Choose β1=1.04,β2=0.7 and other parameters are same as case(2).Then Therefore,the interior equilibriumE∗(0.1424,5.3318,3.2627)is unstable.From the numerical simulation,we note that the system(1)has a stable cycle in Fig.5. Fig 4 Solution of the(1)showing E∗(0.4667,3.8273,5.4682)is stable.The initial value is(1.5,3,5) Fig 5 Solution of the(1)showing E∗(0.1424,5.3318,3.2627)is unstable.The initial value is(1.5,3,5)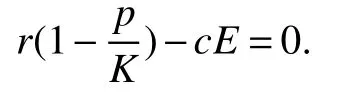
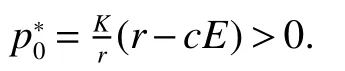
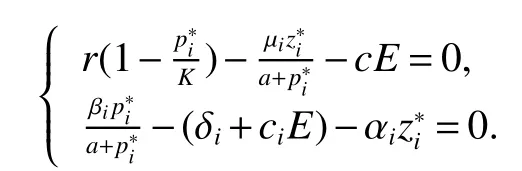
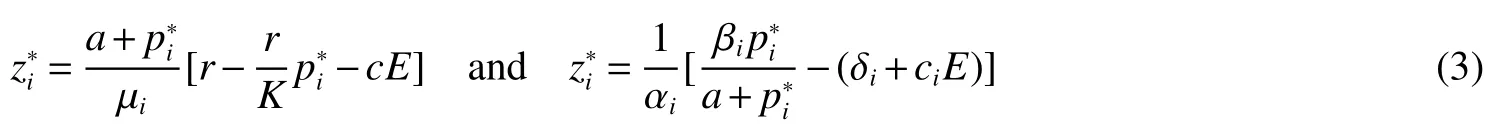

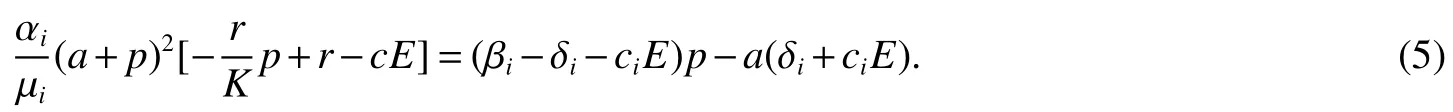
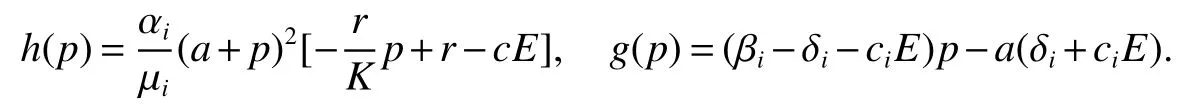
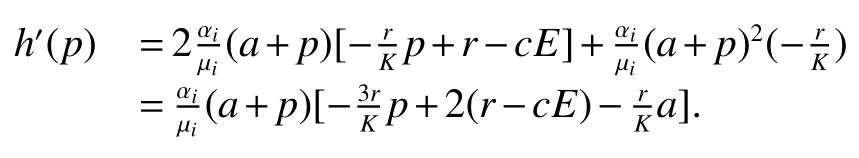

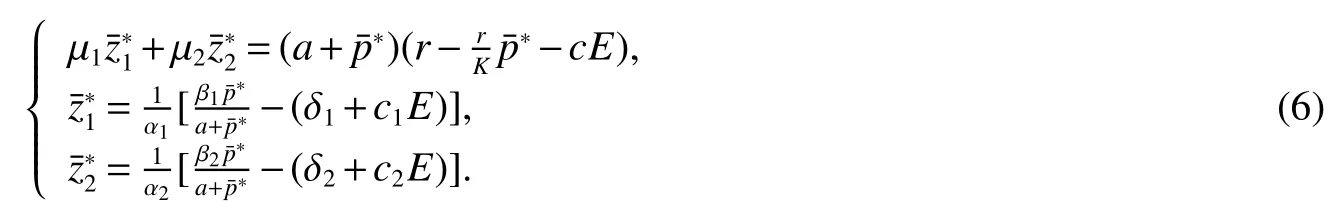
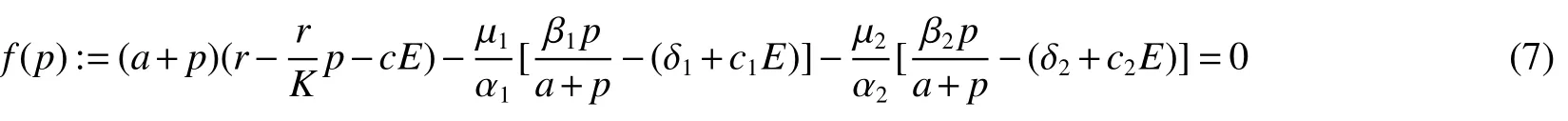

2 Stability analysis
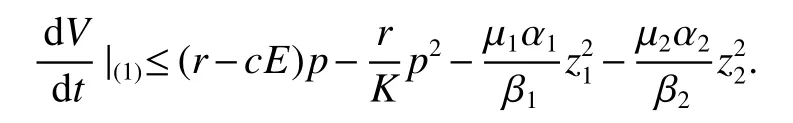
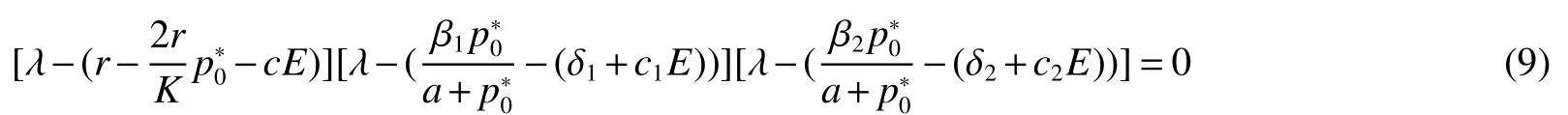
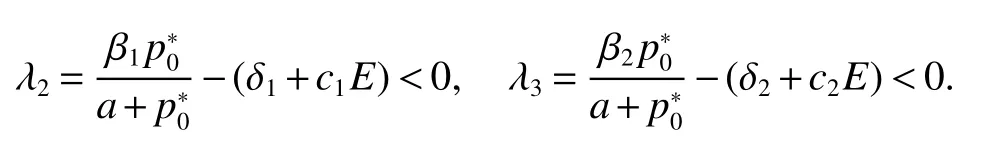
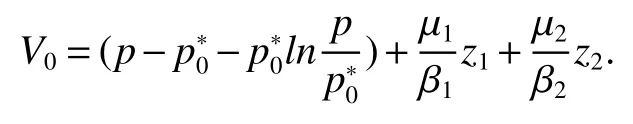
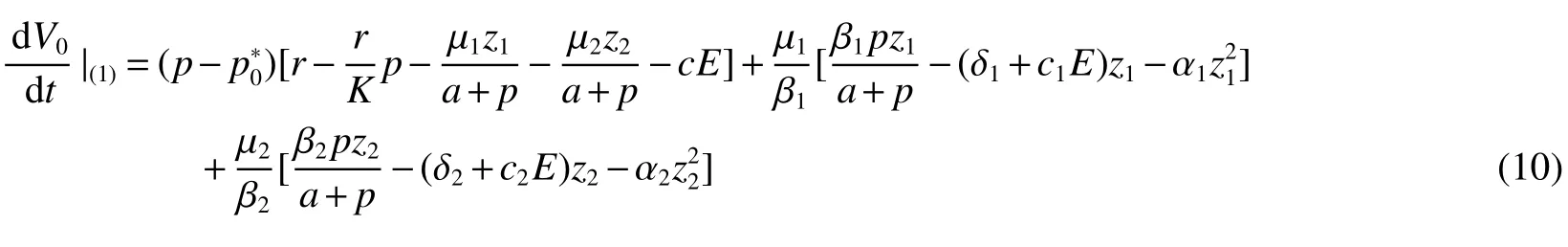
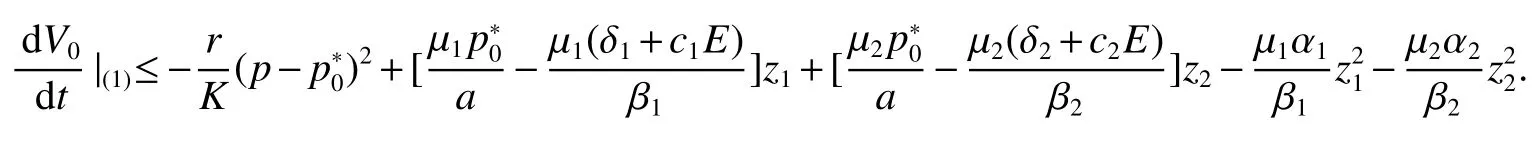
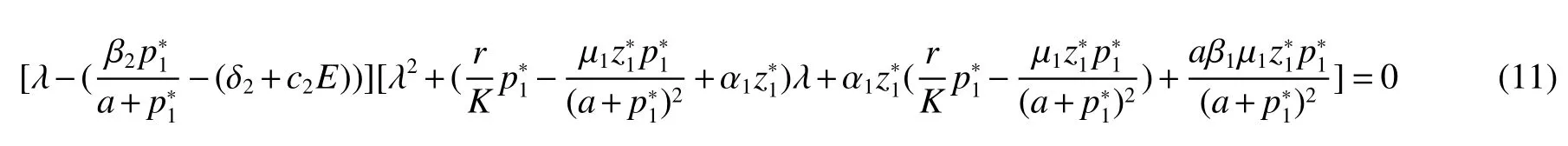
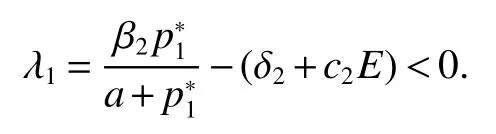

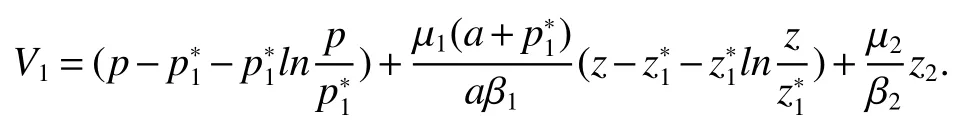
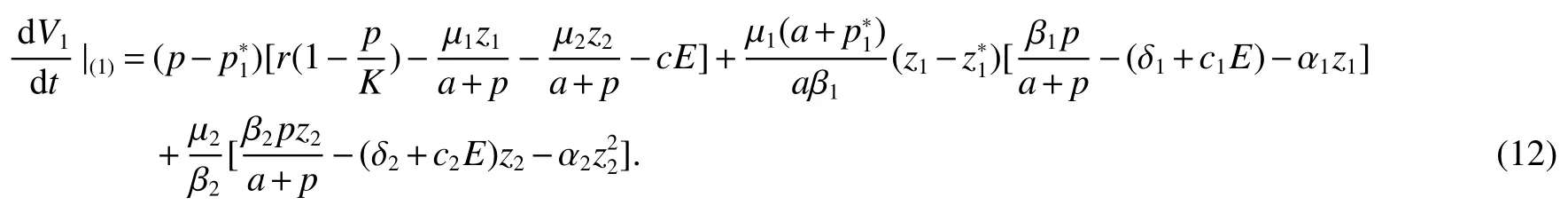

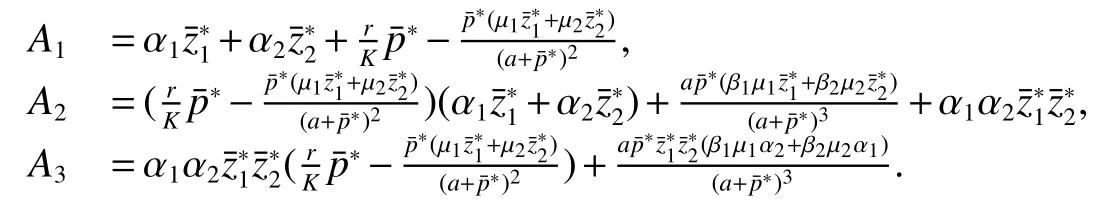
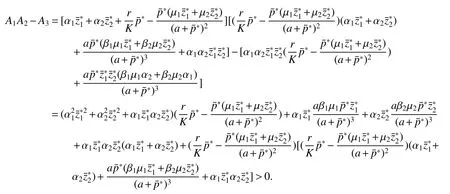
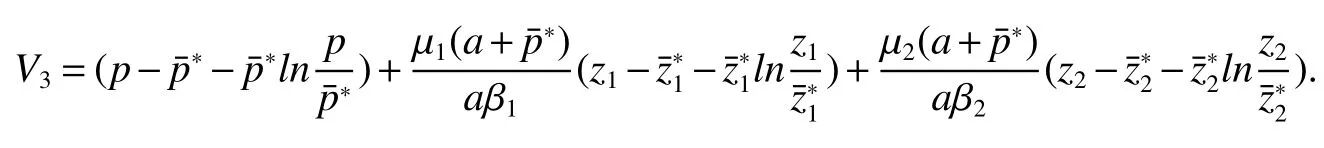
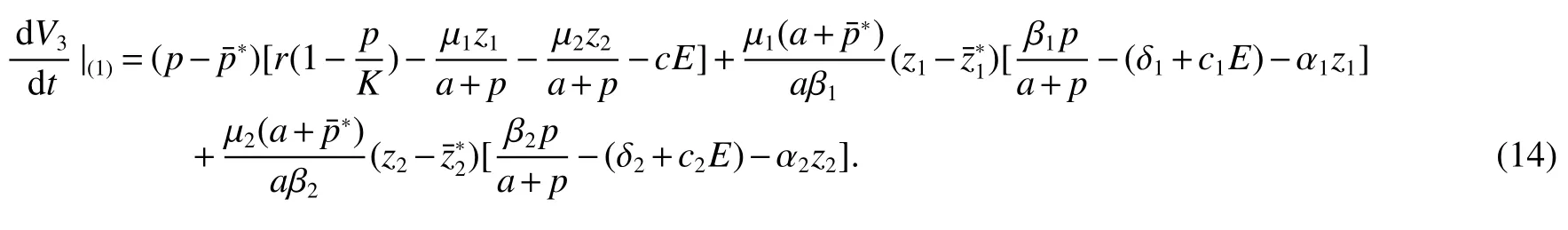
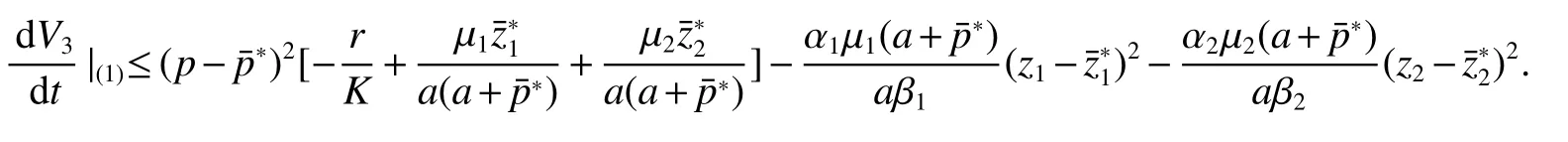
3 Numerical simulation