基于ZFFT频谱细化仿真研究

袁春艳

基于ZFFT频谱细化仿真研究

袁春艳

频谱细化分析是一种重要的频谱分析手段。常见的方法有基于复调制的Zoom-FFT 法、Chirp-Z 变换、Yip-ZOOM 变换等。但是从分析精度、计算效率、分辨率、灵活性等方面来看，基于复调制的Zoom-FFT 方法是一种行之有效的方法，因而应用比较广泛。

文章在介绍复调制Zoom-FFT方法基本原理的基础上，用MATLAB 实现该算法，并通过仿真进行验证，表明该算法能有效细化频谱，且简明、易实现。最后讨论了该算法的运算量和局限性。

引言

在内存和FFT计算长度N有限制的情况下，既要不降低频率分析范围，又要增加频谱分辨率是矛盾的，为了解决只对一个较窄频带的范围进行细致观测的问题，研究者提出了计算窄带谱的频谱细化分析方法。其基本思路是对信号频谱中的某一频段进行局部放大，也即在某一频率附近局部增加谱线密度，实现可选择的频段分析。它是二十世纪七十年代发展起来的一项新技术，其主要目的是识别谱图上的细微结构。频谱细化方法有多种，考虑计算精度、速度、程序实现的难易程度，本文介绍其中的Zoom-FFT算法、相位补偿细化算法和CZT算法三种较为实用的算法，并对前两种方法通过MATLAB进行仿真，对其结果进行了对比验证。

频谱细化的方法

ZOOM-FFT法

复调制Zoom-FFT法（以下简称ZFFT）即复调制细化频谱分析方法，是应用最为广泛的一种选带细化方法，ZFFT能以指定的、足够细致的分析频率轴上任一窄带内信号的频谱结构。在序列变换点数相同的情况下，ZFFT 能获得更加细致的频谱，或者，在相同的频率分辨率下，ZFFT 比基带FFT 需要更少的傅立叶变换点数。因此，ZFFT 非常适合要求大频率分析范围、相隔较密集的频率分辨和少变换点数的场合。

Zoom-FFT算法的关键在于利用傅立叶变换的移频特性，将感兴趣的高频段频率移至频谱原点，降低采样率重新采样，从而获取较细致的频谱。它对于获得某些特殊频段，而不是整个带宽的信号细微谱结构十分有用。

ZOOM-FFT原理分析

复调制细化谱分析方法采用：移频（复调制）—低通数字滤波—重抽样—FFT 及谱分析—频率调整这样一个过程。

设模拟信号为x（t），经抗混滤波和A/D 采样后，得到的离散序列为x（n） （n=0，1， … ，N-1），fs为采样频率，f1～f2为细化分析频带，f0为需要细化的频带中心频率，D为细化倍数，N为FFT 分析的点数，具体算法过程可归纳为如下五个步骤：

抗混叠滤波器

复调制移频

低通数字滤波

重新采样

复FFT处理

与相同点数的直接FFT 相比，这一细化方法所获得的分辨率要高D倍。因为直接进行FFT 分析时，频率分辨率Δf=fs/N ，重采样后的分辨率为Δf=fs/DN ，因此D有时又被称为细化倍数。

MATLAB仿真和验证

为验证上述算法及分析过程的正确性，在MATLAB中产生一个正弦组合信号：

分别利用N点ZFFT 和N/D点ZFFT 对其进行谱分析，仿真条件： f s =1024 Hz，FFT 点数N = 1024，细化倍数D = 32。基带FFT 的频率分辨率Δf= 1 Hz，而ZFFT的频率分辨率Δf′= 1/32 Hz。对信号做N点基带FFT处理后的峰值谱线如图1、2。

由图可知该信号有五个频率成分，且各频率成分间隔小于1 Hz，由图可以看出信号各频谱不易被分辨，相隔较近的几个谱峰叠加为一个谱峰。

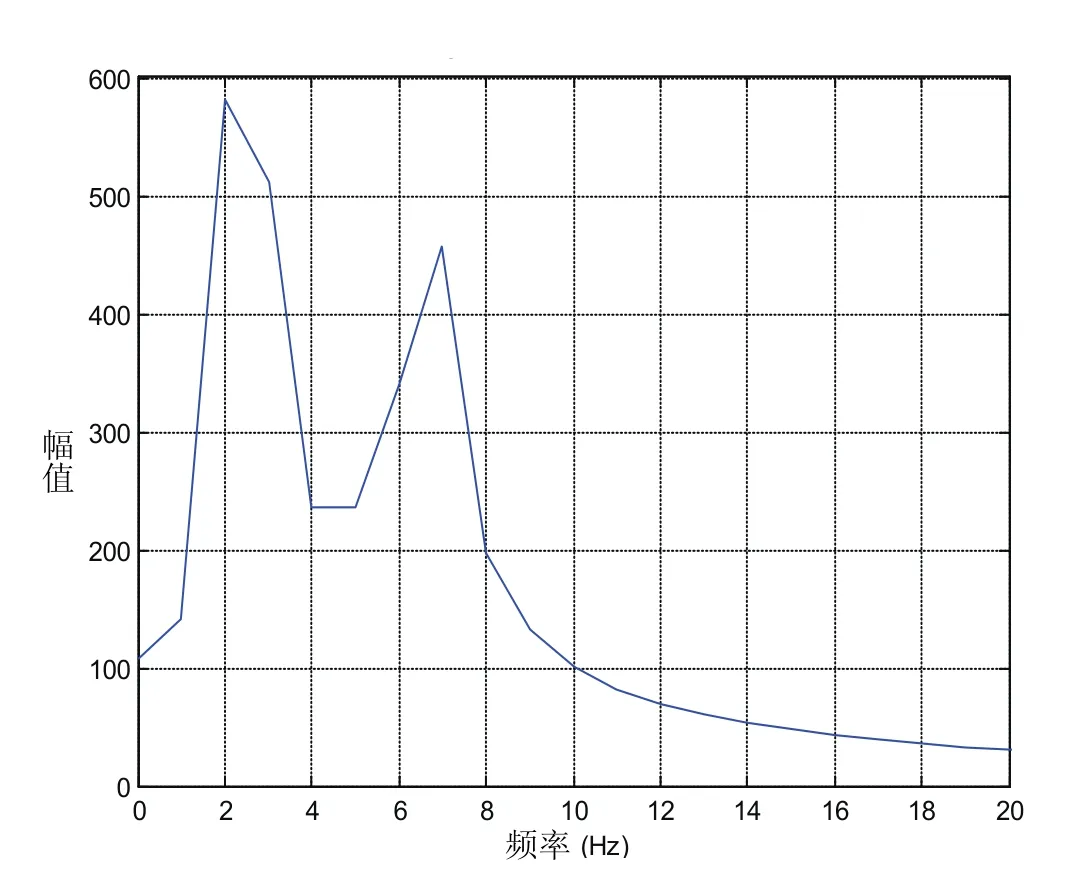
图1　信号频谱图

图2　移频后信号频谱图

图3　重采样后信号频谱图

图4　Zoom-FFT法细化后信号频谱图

细化32倍即需处理32768个采样点，仿真时对x（t）进行离散，离散的点值即为采样值，信号感兴趣的频率范围108 Hz ～124 Hz，采样完成后对采样点移频（中心频率将116 Hz 频率移到原点），可有以下步骤实现：

取f0=116 Hz，w0=2πf0，令f（ t）=exp（-jw0t ）

t取离散化时刻：

则f（t）的离散化可变为：

将两个序列卷积得到的新序列即可实现细化频域的中心频率f0移到原点处。

为了使结果更加直观，仿真时将最低频率108 Hz 移到零点处，图2为移频后基带FFT处理后的幅值谱线。

将移到低频处的信号，按采样频率fs′=fs/D 进行重新采样，采样频率比原采样频率降低了D倍，即对原采样点每隔D 点再抽样一次，可以得到信号x（k） 零点附近的部分细化频谱，如图3所示。

对重采样后的N 点复序列进行复FFT 处理，得到N条谱线，最后得到细化的谱线同原来的排列顺

序是不同，这就必须对细化后的频谱进行调整，使其与原始谱线一致，将上述谱线移至实际频率处即得到细化后的频谱。如图4所示。

此图中，ZFFT的幅值谱线中5 条谱线清晰可见，说明ZFFT效果明显。

若对于移到低频处的信号，按采样频率f s′ = f s /D进行重新采样，对重采样后 N/D 点复序列进行N/D点复FFT 处理，可以得到信号得到信号 N/D 条谱线，这样可以大大降低运算量和采样效率。对频谱进行调整后，这样得到的谱线仍与原始谱线一致，说明ZFFT优势。如图5所示。

ZFFT运算量及局限性

当采用时域抽取FFT算法时，N 点DFT的复数乘法次数为复数加法次数为。为简单起见，仅比较两种算法的复数乘法次数。

图5　降低采样点数后重采样的信号频谱图

设频率分辨率Δf=fs/N ，细化倍数D=Δf′/Δf 。要获得Δf ′的分辨率，基带FFT的运算量为

采用ZFFT 算法，在复调制时只计算重采样的点，需N 次复数乘法。同样，调制系数的计算也需N次复数乘法。设数字滤波器的阶数为K，滤波器系数离线生成，则滤波需要DN•K 次复数乘法，则总的运算量为

随着细化倍数的增加，基带FFT 和ZFFT 的运算量都会大幅度增加；ZFFT 只有当细化频带较窄（此时无需数字滤波）或长序列的情况下，与基带FFT 相比才具有运算量上的优势。

ZFFT算法简明，容易实现，但该算法也存在自身的局限性，但也存在以下问题。

1.细化倍数越高，需要的时域采样点数增加，需要存放中间数据的内存空间巨大限制了最大细化倍数。

2.滤波器截止频率处的频谱不可避免会出现局部失真。

3.细化倍数越高，重采样的选抽比越高，计算量越大。

4.频率成分调整较复杂，算法的灵活性较差。

基于改进Zoom-FFT信号检测方法

信号经过复调制、数字滤波和抽取后，由于将信号从频率（想要观察频段的中心频率）搬移到零频，信号频谱在正频域和负频率变得不对称，这就使得细化后的信号变成了一个复信号，这是细化后信号频谱同原始频谱不一致的根本原因。我们可以通过边带调制的方法使得细化后的信号变成实信号来消除这种不一致。

通信信号检测是一种非合作的方式，要获得对方信息，必须首先检测对方的通信频率， 而检测频点的准确性对后续处理起到非常重要的作用。例如，在某超短波频段中，我们关心的战术电台的信号带宽小于20kHz，信道间隔25kHz，如果我们检测到的信号频率和实际相差较大时，将对解调结果产生很大影响。我们在实际工程中采用了改进的Zoom-FFT信号检测算法，大大提高了信号频率检测的准确性。

小结

实践表明，我们可以看出经过改进Zoom-FFT算法得到的信号的频率值比粗检信号的频率值更加接近载波频率，较大地提高了信号检测的准确性。在实际的工作中，我们成功地将该方法运用到某软件无线电研究项目中，取得很好的效果。将改进的算法运用于实际的通信信号检测中，能够有效提高信号频率检测的准确性。

10.3969/j.issn.1001-8972.2015.10.004