精细结构常数及其测量

刘荣智 郭天太 褚丹丹 吴晓康

精细结构常数及其测量

刘荣智 郭天太 褚丹丹 吴晓康

精细结构常数是研究电磁间相互作用的重要常数。本文首先简述了精细结构常数的基本概念，揭示了在不同情况下该常数表现出来的不同物理本质，然后介绍了精细结构常数的测量方法，以及精细结构常数的研究进展，并指出其值有可能是变化的。

自然界中的各种物理现象，总是包含着一些基本物理学常数，这些常数反映了现象的本质规律，对科学的发展作用巨大。然而在基本物理常数中，只有5个常数才是真正独立的，通过它们几乎可以描写全部物理现象，即真空中的光速c ；Plank常数h （归一化写法为h，h=h/2π）；电子电荷e ；电子静止质量me；阿伏伽德罗常数NA。另外，还有一个常数叫“精细结构常数”（Fine structure constant，FSC），用希腊字母α表示。近些年来，随着人们加强了对α的重视，国际科学界对于α的测量和分析越发关注。

物理学中的一个重要的无量纲数便是精细结构常数。它在原子物理学、电动力学等学科中极为重要。它决定了原子的性质并在电子与质子的相互作用中发挥影响。

精细结构常数也是自然界的基本常数之一，在以下几个方面的具体表现，揭示了在不同情况下该常数表现出来的不同物理本质：

1）α是电子在第一玻尔轨道上运动速度v1与真空中光速c之比；

2）α是电子的经典半径re与康普顿波长λe之比；

3）α是康普顿波长与第一玻尔半经α0之比。

量子电动力学是描述光与电磁相互作用最为完善的理论。其计算表明，不同复杂程度的两个电子之间的相互作用方式，对最终作用的影响也不同，并随作用过程中光子的发射或吸收，以精细结构常数α为底呈指数下降。用α的幂级数可以描述量子电动力学中的所有电磁现象。因此，α被赋予了全新的含义：电磁相互作用的强度。正由于α的重要作用，如何对其进行准确测量倍受关注。

精细结构常数的实验测定方法

α的值，除了可用上述的几种对不同的物理本质进行理论计算的方法得出外，还可用实验测定。将其实验测定得到的值与理论所得进行对比，可验证许多重要的理论。一般取α的倒数α-1作为测量结果。

基于反常磁矩测α的值

1947年，库仑等人从实验中证实了玻尔磁矩µB与电子磁矩µe间存在着一个差异αe，他们将其称为电子的反常磁矩，并精确测定其值为：

量子电动力学给出了αe与α的关系为：

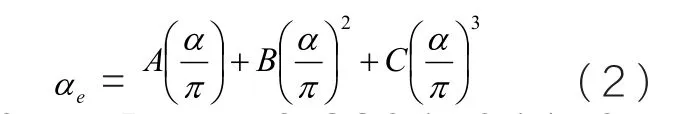
式中，A=0.5，B= -0.3284784458，C=1.184±0.007，从而测出常数的值为：

基于测定2e/h 的值测α的值

根据约瑟夫森效应，交流的频率ν与电压U之间的关系为：

通过测定ν和U即可确定2e/h的值。而量子电动力学给出2e/h 和α之间的关系为：

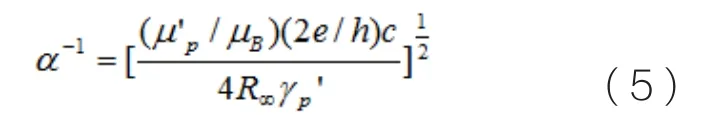
式中，γp'为水中质子的回旋磁比，µp'/µB是以玻尔磁子为单位的水中质子的磁矩，均有较准确的实验数据。用这种方法测得α值为：

基于氢的超精细结构分裂测α的值

除精细结构以外，在光谱中，若考虑核的磁矩和自旋，还有超精细结构。氢的超精细结构分裂是指氢原子光谱中LS1/2的两条谱线的频率差为ΔυH。在1970年，海尔威格等人从实验中精确测得两条谱线的频率差ΔυH的值为：

量子电动力学给出了ΔυH与α的关系为：

式中，r=µ'/µ为质子与电子的磁矩比，µB为玻尔磁子，µ为电子磁矩。可得出的α值为：

基于ì子素来测α的值

一种测定方法是使用ì子素（由正ì介子和电子形成的原子）的基态超精细分裂来精确测量。这种分裂主要变化为它可以被很准确的计算。ì子素是一种纯粹的轻子系统，由于它的质子的结构，在氢气超精细结构的计算上不存在困难。

2006年的CODATA报告中提到在1982年和1999年，在LAMPF（劳斯阿拉莫斯国家实验室）开展了关于精细结构常数测定的分析。所得到的值是：

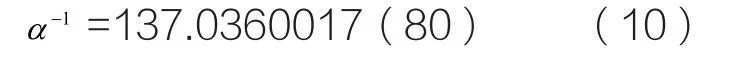
这个值的相对不确定度是5.8×10-8，其主要来源是ì介子对电子的质量比。

原子精细结构也随α2R而发生变化。然而，在氢原子中，

∞2P1/2-2P3/2能级分裂的测定（约11GHz）被2P级（100 MHz）的固有宽度限制。于是，最好的2P1/2-2P3/2能级的不确定度测量只有15 kHz，相应地有约1.4×10-6的相对不确定度，并可提供了一个在7×10-7这个精度水平的α值。氦的结构对于测定精细结构来说相对要好一些，因为它在23PJ的精细结构中，有30GHz的分裂频率和1.6MHz的固有宽度。相应的间隔已经通过射频光谱，以及通过23Sl-23PJ线的激光光谱被精确测量，最好的结果存在着2.4×10-8的相对不确定度。

以上介绍的几种方法测得的α值在准确度允许的范围内可认为相同，并且也与理论值十分接近，这足以说明量子电动力学是描述光谱的基本理论。

精细结构常数的研究进展

随着人们对精细结构常数研究的重视程度日益增加，测得更加精确的α值的新方法不断地出现，并已取得重要的进展。而对于α值是恒定的还是变化的，国际科学界已日益形成共识。国际科技数据委员会（CODATA）于2010年给出的精细结构常数的标准值为α=137.035999074（44）。

精细结构常数测定的最新进展

在理论方面，氢原子和氦原子的电子系统的量子电动力学（QED）计算是非常困难的，目前在理论值与测量结果之间还存在一定的不一致。Pachucki和Yerokhin通过计算所有QED的项达到量级α5R∞克服了这个难题。它们得到的值是：

式中，第一个不确定度是根据理论得出，第二个是根据实验得出，相对不确定度大小为3.1×10-8。这个值和其他α的测定值完美一致。

最精确的α值的测定能从电子奇异点ae的测定中被推理出。在十几年前，最佳的ae测得值是由华盛顿大学获得的，其相对不确定度为3.7×10-9。在2006年，哈佛大学的Gabrielse将不确定度降低了大约6倍，取代了之前的结果。在2008年，Gabrielse再一次改进了ae的测量，得到2.4×10-10的相对不确定度。整个过程中，电子奇异点的QED计算被连续不断地改进。

在从ae的测定推理出α值上看，在2006年，Kinoshita小组通过将实验的与理论的结果结合起来，得到了精细结构常数的值α-1=137.035999710（96），这个值的相对不确定度是7×10-10。这个测定结果的值被收录在CODATA的2006年的报告中。然而，在2007年，Kinoshita和他的合作者们发现在α4计算中存在一个错误，在改正之后，α的值变成了α-1=137.035999070（98）。

最终，精细结构常数的值从最后一次ae的测定中被推断出来，其大小为：

它的相对不确定度大小为3.7×10-10，这是目前最精确的α测量结果。

精细结构常数有可能是变化的

1997年I.Levine等人提出的报告，说明了原子碰撞时的动量转移的过程中，α值会随之发生变化。具体来讲，高能时的α的值比它在低能时增大了约7％，即α值并不是固定不变的。这一发现引起了科学界的广泛关注与讨论。

美国的《物理评论快报》这一期刊在2001年8月报道了多国科学家研究组对类星体光线的观测结果。类星体的光谱红移非常大，可按哈勃定律推算出其距地球过百亿光年。研究小组利用在红移范围观察类星体这一研究方法，两年时间观测了137个高亮度类星体，实质上就是研究它们在宇宙早期发出而如今才到达地球的光。利用光通过星际物质时由能量的吸收而在光谱上出现暗线的位置，可推导出α值，而不同化学元素的吸收谱线间隔取决于发生能量吸收时红移中α的任何微小变化。研究小组把观察到的谱线间隔与在实验室获得的值比较，发现宇宙早期的α值比现在小了约7×10-6。

上述研究方法的优点是可以探测宇宙大部分历史中的精细结构常数值。P.P.Avelino等人于2000年在《物理评论快报》上发表的文章和R.A.Battye于2001年在同一刊物上发表的文章，均根据宇宙微波背景辐射（CMB）的观测结果表明在宇宙早期，α值比现在小百分之几。

对于已观测到的α在不断变化这一现象，部分学者认为这是Planck常数h和真空中光速c在早期宇宙时都比现在大而造成的。

结语

目前，对精细结构常数（FSC）的研究和探索意义重大且包含了特殊的价值。随着研究的深入，越来越精确的值被不断提出。而最新的研究表明精细结构常数有可能是变化的，这一认识对于加深人类对于自己生活在其中的宇宙的认识，无疑具有重要的意义。

10.3969/j.issn.1001-8972.2015.17.007