基于CFX接口运用的气动弹性研究
谢 萌
基于CFX接口运用的气动弹性研究
谢 萌
CFX软件可以允许用户借助CEL和CCL定义自己的函数,能够识别Fortran语言,为用户提供了一系列不同层次的接口程序,方便用户使用。本文使用Fortran语言编写了自己所需的物理模型,使用CFX中的User CEL Function功能调用,将动网格技术结合CFX求解非定常气动力的方法运用与气动弹性的研究中。
网格运动技术
由于计算非定常气动力,翼型要运动,所以利用了CFX中的网格运动技术。在CFX计算中网格运动方法有:(1)给定每个时间步物面网格相对于初始时刻的位移,根据经典弹簧方法得到各个网格点的位移;(2)给定每个时间步物面网格的具体位置,即给定每个时间步的网格等。这两种方法都能用CEL或FORTRAN语言来实现。见图1。

图1 网格运动的实现
从上图可以看出,本文中用的方法是给定物面每一时刻相对于初始位置的位移,然后其他点的运动通过弹簧方法算出。其网格运动技术是采用了弹簧方法,本文中所使用的弹簧刚度如下:
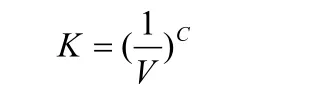
其中K代表弹簧刚度,V代表单元体积,C是刚度指数,本文的计算中C取10。但刚度值只能限制在10-15和1015之间。
在计算物面各个网格点的位移时使用了CFX提供的用户程序接口User CEL Function来编程实现。
非定常气动力的验证
非定常气动力的准确计算是气动弹性研究的基础,本文选择验证非定常气动力的经典算例,并将计算结果和实验结果做了比较。翼型运动规律为
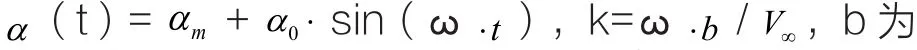
翼型的半弦长。转动轴位置和力矩积分点位置都为0.25倍弦长处。模型以及状态如下:

图2和图3给出了上述两个计算模型Cl和Cm的计算结果与实验结果的比较。
从整体的计算结果中可以看出,本套网格、参数设置和算法是可靠的,具有较高的精度。
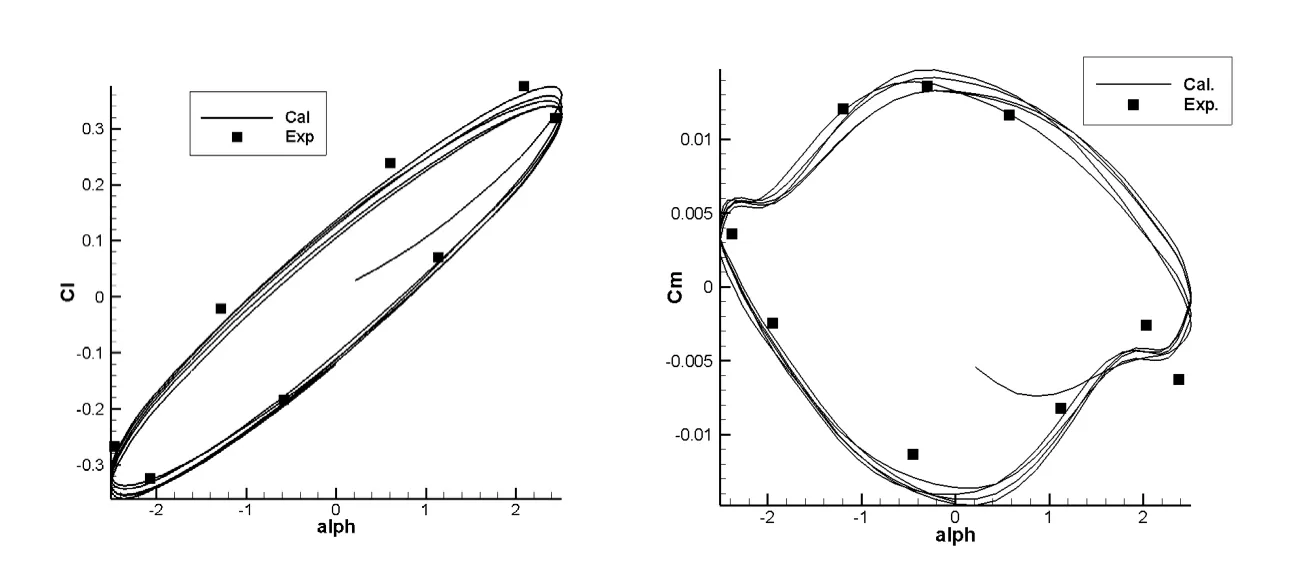
图2 NACA0012翼型俯仰振荡运动中瞬时升力系数Cl和力矩系数Cm随瞬时迎角的变化规律与实验结果的比较
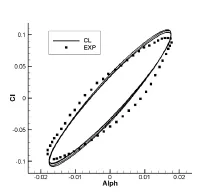
图3 NACA64A010瞬时升力系数Cl随瞬时迎角的变化规律与实验结果的比较
结构运动方程的求解
认为结构为小变形,弹性力在线性范围内,翼型具有典型的两个自由度(沉浮h和俯仰α),则其动力学方程为:
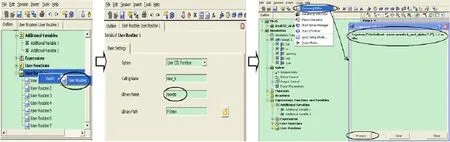
图4 CFX软件添加Fortran代码过程图
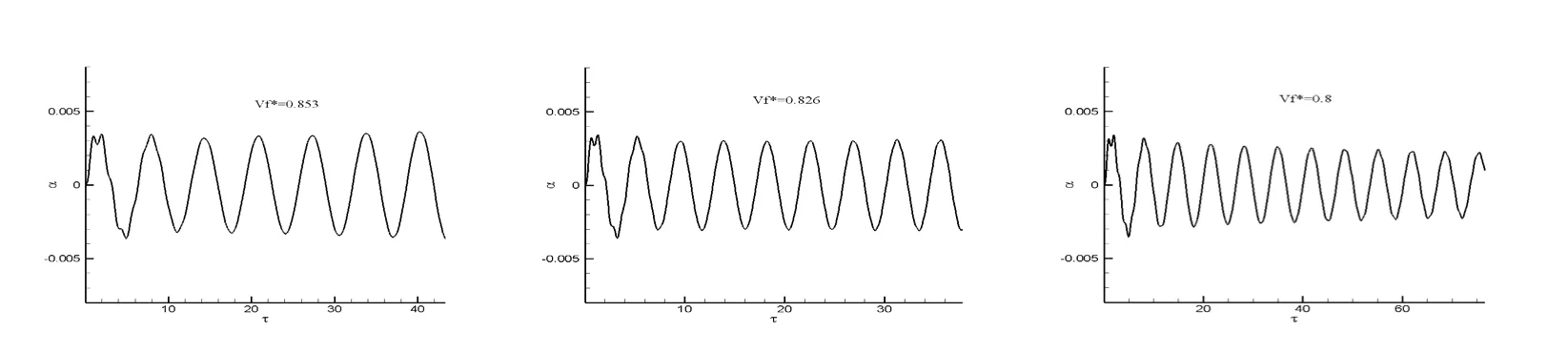
图5 M=0.8时Isogai Wing在不同速度下的响应历程

其中,m为翼型质量,Sα为静矩,Iα为翼型的转动惯量,Kh和Kα分别为支撑翼型的沉浮弹簧刚度和俯仰扭转刚度,L为翼型的升力,Mz为俯仰力矩。
在求解结构动力学方程时用的是显式的四阶线性多步法,L和Mz由非定常流场求解器直接提供。流场求解器每求得一次气动力以及力矩,将其传给结构运动方程,得到这一时刻的运动参数,同时,再将运动参数传回流场求解器,得到下一时刻的力和力矩,如此循环获得翼型运动规律,判断结构在该状态是否稳定。
如前所述这也是通过CFX的User CEL Function功能来编程实现的,每步求解时流场求解器都会首先调用程序来求解出网格的运动情况,算出物面边界上各点的位移,进而求解流场。动网格技术与前面所述的相同。
经使用和分析我们发现这是利用此软件来模拟颤振非常的直接简便,从计算结果上看来也是比较可靠的,但缺点是时间步要比较小,导致计算时所需时间较多,有待进一步研究更高效的允许更大时间步的计算格式。
气动弹性的验证
对于给定的飞行器结构,当飞行速度由小到大时,振动会由衰减逐渐变成发散,在这中间的某一速度时,扰动引起的振动振幅恰好维持不变,此时的速度即为颤振临界速度。对飞行器而言,发生颤振是一件非常危险的事。
本文中选择给定结构参数的二维翼型,通过计算寻找在不同马赫数下的颤振临界速度,然后经过对比验证以确保算法的正确性。
本文气动弹性的验证采用CFX软件调用Fortran程序来实现。图4中描绘了调用程序的前期编译过程以及对外部程序编译。具体做法如下:
首先,要依照CFX软件中规定的格式编写User CEL Function的Fortran代码。然后将外部程序添加到CFX中,然后再对程序编译。图4中编译命令中的“h_and_alpha”为Fortran代码所在文件夹名称。点击process后,生成winnt文件夹,此时编译完成。winnt文件夹中即包含了CFX在求解过程中需要调用的所有文件。
编译完成后即可写出计算文件,开始计算。
选用NACA 64A010翼型作为研究算例。参考跨音速气动弹性标准模型Isogai Wing设计结构参数,在相同的无量纲结构参数及计算状态时,通过与Alonson&Jameson 和Liu et al 计算结果的比较可以看出,本文所使用的方法具有一定的准确性。需要注意的是在CFX中求解的是有量纲的结构方程,而给定的结构参数为无量纲的参数,所以需要进行转化。
图5中给出了M=0.8时该翼型在不同速度下的响应历程,从图中可以看出临界点应该在Vf=0.826附近。跟文献中给出的临界点比较接近。
总结
使用CFX调用外部所需物理模型,在CFX软件中进行编译并通过标准算例验证了该方法研究气动弹性问题的可行性。
10.3969/j.issn.1001-8972.2015.15.006

