基于小波消噪的主轴回转精度动态测量法
张 丹,侯 力,曾颖峰,西庆坤,王 瑞
(1.四川工程职业技术学院车辆工程系,四川德阳 618000;2.四川大学制造科学与工程学院,成都 610065;3.东方电气股份有限公司风电事业部,四川德阳 618000)
基于小波消噪的主轴回转精度动态测量法
张 丹1,2,侯 力2,曾颖峰1,西庆坤1,王 瑞3
(1.四川工程职业技术学院车辆工程系,四川德阳 618000;2.四川大学制造科学与工程学院,成都 610065;3.东方电气股份有限公司风电事业部,四川德阳 618000)
主轴回转精度是影响零件加工精度的主要因素之一。针对传统的傅里叶变换对主轴回转误差运动的采样信号进行消噪时,使用低通滤波器会损失主轴回转误差运动某些有用成分的问题,提出了基于小波变换的消噪滤波方法对主轴回转误差进行动态测量。文章在分析主轴回转误差的测试原理和信号特点的基础上,通过选用合适的小波基和阈值分离出基准球安装偏心误差,信号的信噪比由初始值15.447db提高为18.105db,去噪效果明显。实验结果表明,采用文中方法对C616主轴回转精度进行测量,其测量结果与DJ-HZ-1型机床回转精度测量分析仪的测量结果基本吻合。
回转精度;动态测量;小波消噪;信噪分离;信噪比
0 引言
主轴回转精度是反映机床主轴回转时轴心线在空间所产生的运动误差[1]。一般情况下,主轴回转误差运动具有随机性,表现为高频噪声[2]。但主轴回转误差的测量受到主轴安装偏心、测量基准的形状误差等周期性因素的影响,使得传感器通常采集到的实际信号中常含有低频成分,采样信号的频率特性随时间变化的,属于非平稳信号[3]。采用传统的傅里叶变换对采样信号进行消噪时,将信号在整体上分解为不同的频率分量,该方法缺少时域定位的功能,不能有效地分离采样信号,在使用低通滤波器时会损失主轴回转误差运动的某些有用成分。
小波变换是20世纪80年代后期发展起来的一门新兴的应用数学分支,目前已广泛引入到工程振动信号分析等领域中。小波变换具有多尺度特性,通过适当地选择基本小波,可使小波变换在时域和频域都具有表征信号局部特征的能力。由于小波变换具有自动变焦功能,利用小波变换对非平稳信号进行消噪,可有效区分信号中的突变部分和噪声[4]。
本文以刀具固定的车床为例,从研究主轴回转误差运动的测量原理出发,提出利用小波消噪算法对传感器拾取的综合误差信号进行信噪分离,从混有周期性低频成分的采样信号中提纯主轴回转误差,以期提高车床主轴回转误差的测量精度。
1 测量原理
工程上研究误差运动对加工的误差影响,通常简化为测量回转误差运动中对加工精度影响最大的那个方向(误差敏感方向)上的分量[5]。车床主轴回转误差在径向方向的分量将以等比例的关系转化为加工误差,而在轴向方向的分量对加工表面的影响极小。因此,动态测量主轴回转精度时,一般只需布置一个传感器就可得到车削加工时的误差敏感方向。此外,为解决主轴回转轴线看不见的问题,通常选用高圆度的圆球作为基准面来体现回转轴线[6]。如图1所示工件回转型主轴,装有基准球的标准芯轴通过三爪卡盘与主轴相连,电涡流传感器、霍尔传感器的检测头固定在特制的支架上。当主轴回转时,电涡流式传感器的输出信号可描述为
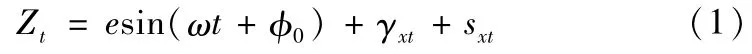
式中,e—基准球的几何中心相对主轴回转中心的偏心量;ω—主轴回转误差运动角频率;φ0—初始相位角;γxt—主轴回转误差运动在固定敏感方向的投影;sxt—基准球在敏感方向的表面形状误差。
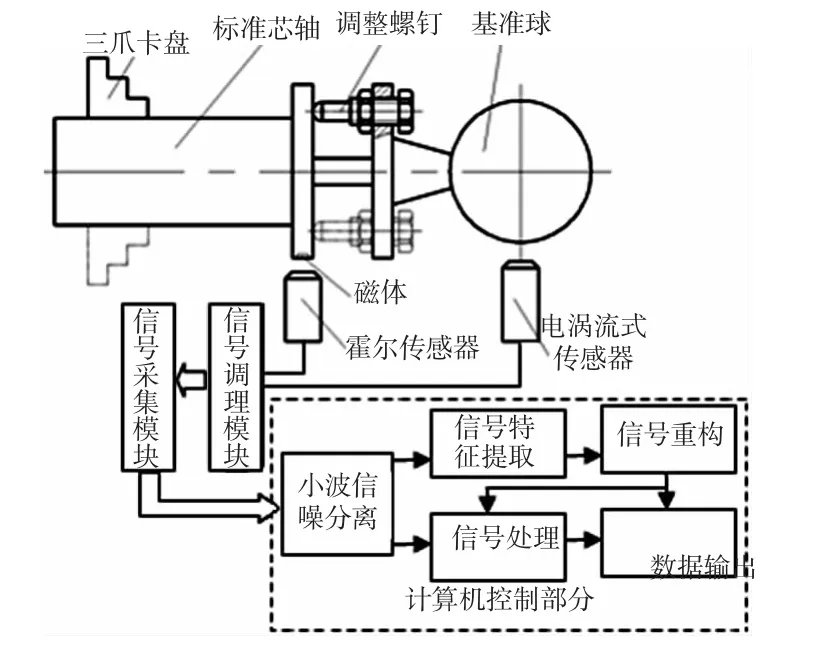
图1 测试系统原理图
由于采用高圆度的圆球作为测量基准球,故基准球的形状误差sxt可忽略掉,式(1)可变为
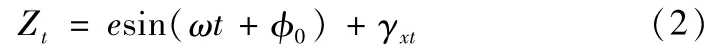
从式(2)可知,电涡流式传感器拾取到总误差信号由基准球偏心安装误差信号和主轴回转误差运动信号组成。其中,偏心误差e sin(ωt+φ0)是个平稳的正弦信号,其频率不会随时间变化;而主轴的跳动情况γxt常常是随机的,其频率随时间不断变化。通过分析传感器采样信号的特征,根据小波消噪算法对Zt进行信噪分离处理,获得评定主轴回转误差的数据γxt,则式(2)最终变为

2 小波变换
将任意L2(R)空间中的函数z(t)在小波基下进行展开,称作函数 z(t)的连续小波变换(简称为CWT),其表达式为[7-8]

式中,WTz(a,b)—小波变换系数;a—尺度因子,反映特定基函数的尺度;b—平移因子,指明平移的位置。
由连续小波变换的定义可知,小波变换和傅里叶变换都属于积分变换。但小波变换又不同于傅里叶变换,由于小波基具有尺度a和平移b两个参数,就可以使小波变换在时域和频域都具有表征信号局部特征的能力。
若小波变换满足条件式(5),则其反变换存在。
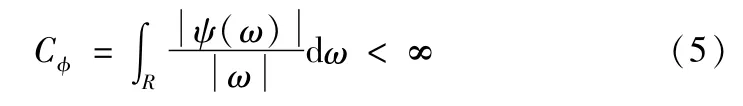
连续小波变换的反变换表达式为

3 小波消噪原理
信号消噪是小波分析的重要应用之一。含噪的一维信号模型可表示为[9]
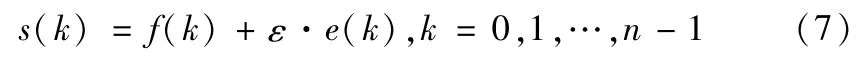
式中,s(k)—含噪信号;f(k)—低频信号,工程实际中通常表现为比较平稳的信号;e(k)—噪声信号,通常表现为高频信号。
对信号s(k)小波消噪的实质是抑制信号中的高频成分,增强信号中低频成分的过程。该过程是利用小波分析对信号s(k)进行小波分解,由于噪声信号e(k)多包含在具有较高频率的细节中,从而可利用门限、阈值等形式对分解所得的小波系数进行处理,然后对信号进行小波重构即可达到对信号消噪的目的。小波分解的一般过程如图2所示,分解关系为

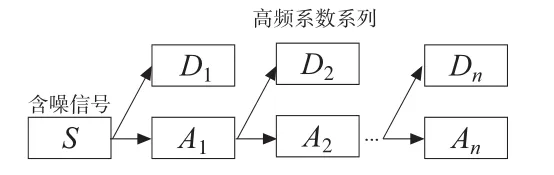
图2 小波信号多尺度分解示意图
4 测试系统
4.1 硬件组成

图3 主轴回转误差测试现场
本文在C616车床上进行主轴回转精度动态测量,测试现场如图3所示。本系统主要由计算机和测量仪器系统组成,配置有美国NI公司的数据采集卡(DAQ)的计算机用于快速高效完成数据采集,取样、转换和后期处理,测量仪器包括;OD9000型电涡流式传感器,量程为1mm,探头直径为4mm,起始间隙为φ0.5mm,输出电压在0~5V之间;NJK-5002型霍尔接近开关,接近时为0电平,离开时为1电平,工作电压在6~36V之间;调理电路模块,5通道4阶低通滤波器放大器,截止频率为1000Hz,放大倍数1~320倍可调;NI公司的PCI-6024E数据采集卡。
4.2 测试结果分析与处理
测试条件;车床型号C616;室温20±0.5℃;主轴转速530转/分;45#钢基准球尺寸φ10.18mm。
测试软件;利用LabWindows/CVI编制上位机程序并用Active X控件调用Matlab中的小波工具箱。
根据本文方法对车床主轴回转误差进行测量,取fs=1024Hz。图4a为电涡流传感器原始输出信号的时域波形,其信噪比为15.447db;图4b为原始信号的功率谱,该谱图含有一个幅值最高的频率8.83Hz,由标准球安装偏心产生;图5选择db3正交小波基对原始信号进行4层小波分解,其中a1~a4、d1~d4分别表示逼近信号和细节信号;图6a是对原始信号进行了默认阈值去噪处理后,在小波分解第4层的低频重构,其信噪比为18.105db,可见其去噪效果明显;图6b对低频重构信号进行功率谱分析,与图4b对比,原始信号中的高频成分滤除掉了;图7消除低频成分后获得的噪声信号及其功率谱,与图4b对比可知,低频成分(安装偏心误差)从原始信号中滤除了;图8将噪声信号叠加在基圆上形成圆图象,再利用最小二乘圆法对圆度误差进行评定。

图4 原始信号及其功率谱(n=530 r·min-1)


图5 小波分解后各层逼近信号及细节信号(db3)

图6 默认阈值消噪后的信号及其功率谱

图7 噪声信号及其功率谱
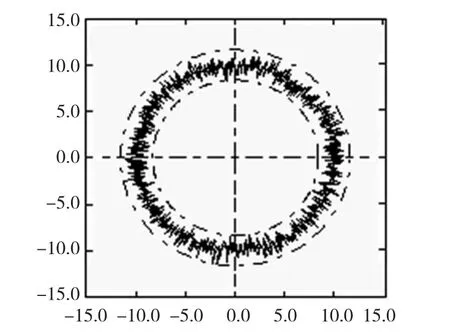
图8 噪声信号叠加在基圆上形成圆图象
根据误差理论的分析,用单个样本(本文指回转圈数)来评定误差较大,增加所取的样本数可提高测量精度。从本实验的具体情况考虑,取10个样本数作为分析对象。表1为当主轴转速为530 r·min-1、750 r· min-1、900 r·min-1时,采用本文方法分别测量的10圈主轴回转精度的圆度误差值并求其均值,然后在相同的实验条件下,利用重庆迪佳科技有限公司的DJHZ-1型便携式机床回转精度测量分析仪进行验证,得到两种测量方法下的主轴回转精度。

表1 C616车床主轴回转精度实测结果对比
从表1的圆度误差值可看出,主轴回转精度的平均值随着转速的增加有递增的趋势。与DJ-HZ-1型机床回转精度测量分析仪的测量结果相比较,本文方法的测量结果精度更高。因此本文提出的基于小波消噪的动态测量法能实现信噪分离,方便、准确、可靠地测量主轴回转误差。
5 结束语
小波变换的自动变焦功能对非平稳信号的消噪有着传统傅里叶变换不可比拟的优点,因此小波消噪成为小波分析最重要的应用之一。根据主轴回转误差运动的非平稳特性,提出了一种基于小波变换的信号消噪方法。该测量方法与虚拟仪器设计工具LabWindows相结合,利用Active X控件调用Matlab中的小波工具箱,通过选用合适的小波基和阈值实现了基准球安装偏心量与主轴径向回转误差的有效分离。采用本文方法对C616主轴回转精度进行测量后,并与重庆迪佳科技有限公司的DJ-HZ-1型便携式机床回转精度测量分析仪的结果相比较,本文方法的测量精度有所提高。
[1]高慧中,刘飞,梁霖,等.基于遗传算法的主轴回转误差评价方法[J].组合机床与自动化加工技术,2012(12);19-22.
[2]Shoji Noguchi,Tadao Tsukada,Atsushi Sakamoto.Evaluation method to determine radial accuracy of high-precision rotating spindle units[J].Precision engineering,1995,17(1);266-273.
[3]吴新杰,杨洋,许超,等.基于小波变换处理圆度误差的测量方法[J].仪器仪表学报,2008,29(9);1961-1964.
[4]戴龙成,宣益民,尹健,等.小波消噪及其在传感信号处理中的应用[J].兵工学报,2003,24(2);257-260.
[5]黄惟公,董仲林.机床主轴回转精度数字测量法及其仿真[J].四川工业学院学报,1999,18(3);1-4.
[6]毛剑峰,邹鲲,周勤之.基于球标法的高精度主轴回转误差测量[J].组合机床与自动化加工技术,2013(12);108-111.
[7]谢文涓,蔡改贫.回转体零件表面形状误差分析的小波变换方法[J].组合机床与自动化加工技术,2010(11);29-34.
[8]贾伟广,胡丹,车畅.基于小波分析和支持向量机的刀具故障诊断[J].组合机床与自动化加工技术,2010(12);65-67,70.
[9]陈渊.基于改进阈值函数的提升小波变换超声信号去噪研究[J].组合机床与自动化加工技术,2010(9);48-51,55.
(编辑 李秀敏)
Dynamic Measurement for Error-Motion of Spindle Rotation Based on Wavelet De-noising
ZHANG Dan1,2,HOU Li2,ZENG Ying-feng1,XIQing-kun1,WANG Rui3
(1.Vehicle Engineering Department,Sichuan Engineering Technical College,Deyang618000,China;2.School of Manufacturing Science and Engineering,Sichuan University,Chengdu 610065,China)
;Error-motion of spindle rotation affecting the machining accuracy of parts is one of main factors. Due to de-noising of spindle rotation error-motion with low pass filter in traditional fourier transform caused the loss of some useful signal,dynamic measurement for error-motion of spindle rotation based on wavelet de-noising is put forward.After analyzing the measuring principle and characteristic of the rotation error,the eccentricity error caused when installing standard ball is separated by selecting appropriate wavelet base and threshold value,and the signal-to-noise ratio is increased from 15.447db to 18.105db.Experimental result showed that the rotation precision on C616 with the proposed method in this paper was in accordance with DJ-HZ-1 machine tool rotation precision measuring instrument.
;rotation precision;dynamically measure;wavelet de-noising;signal-noise separation;SNR
TH165;TG806
A
1001-2265(2015)05-0073-03 DOI:10.13462/j.cnki.mmtamt.2015.05.020
2014-08-10;
2014-10-25
张丹(1983—),女,四川资阳人,四川工程职业技术学院讲师,博士,研究方向为机电一体化,(E-mail)shirley831006@163.com。

