再入反舰导弹多弹协同饱和攻击突防最优弹道研究

李聪颖 韩蕾 高晓冬 杜小雪

航母编队具有较强的防空能力.美航母编队远程防空区主要由E-2C空中预警机、编队舰载远程对空警戒雷达、EA-6B电子战飞机和F-14战斗机(F/A-18战斗攻击机)负责,以发现来袭的敌空中飞机、导弹舰艇及远程反舰巡航导弹.必要时,还可得到侦察卫星、空军E-3空中预警机、EC-135电子侦察机以及F-15、F-16战斗机等兵力的支援.美海军称其为“第一道防线”,即远程侦察警戒线,其具体任务可概括为:争取在敌来袭的飞机和舰艇发射导弹之前将其发现,并引导己方空中兵力对其进行拦截和干扰;发现敌方已发射的巡航导弹,及时向航母编队报警,进行目标指示,保障各道防线的兵力、兵器进行有效干扰或抗击.航母编队远程防空区的主要任务是探测预警,其核心组成为E-2C空中预警机和以“宙斯盾”防空导弹武器系统为主的编队舰载远程对空警戒雷达.

为打击航母编队等具有较强防空能力的舰艇目标,必须突破舰载防空区的拦截.在末端舰载拦截导弹杀伤区域内,拦截弹可以捕获滑翔弹头,预测其飞行弹道,并实施拦截.传统突防方式强调导弹机动性的提升[1−3],在拦截区域内,滑翔弹头进行一定的规避机动,以降低敌方对弹道的预测精度,减小拦截概率.滑翔弹头的规避机动可根据拦截导弹的飞行能力和敌方拦截态势等选择适当时机进行.

由于航母编队具有很强的对空防御能力,对反舰导弹的超视距全方位立体防御系统日益完善,它以体系结构方式组织对抗,从而在最大限度内摧毁来袭导弹.在这种条件下进行突防,仅仅依靠导弹武器自身的突防技术,如隐身技术、多弹头技术、超低空超高速技术等,愈来愈难以突破敌方防御体系,而体系对抗突防技术将成为首选.体系对抗突防[4]的重要手段是导弹协同攻击:即在一定的战术思想指导下,充分利用各弹自身的性能特点和相互间的战术、技术配合,从而达到突防效果倍增的作用[4−6].

现代舰艇拥有多种防御措施来应对反舰导弹,例如舰空导弹系统,电子对抗系统和近程防御武器系统(Close-in weapon system,CIWS).海面舰艇的CIWS能够探测到来袭的反舰导弹和战机,并能在较小范围内将其摧毁.该系统由联合雷达、火控系统和多重速射火炮组成,对再入反舰导弹来说,该防御系统无疑成为其最大的障碍.如果同一批次的再入反舰导弹能够在某一时刻同时攻击目标,那么将造成舰艇CIWS的瞬时防御达到饱和,从而有利于突破其防御体系.

饱和攻击技术的实现,还要对末端攻击角度进行一定的约束.近年来,国内外有些学者研究了同时考虑导弹攻击时间控制和攻击角度控制的问题.文献[7]通过解最优控制,给出了一种攻击时间和攻击角度控制的闭环制导律.文献[8]研究了导弹攻击时间和攻击角度控制三维导引律的设计问题,给出了如何用几何的方法来设置航路点通过角和期望攻击角度的方法.文献[9]所采用的方法是首先将导弹导引到指定的航线上,然后在直线飞行过程中规划出一条机动飞行航路以消耗多余的剩余时间,最后再飞回到该航线上以获得攻击时间和攻击角度控制.

1 再入反舰导弹约束条件分析

与一般再入飞行器的轨迹优化不同,再入反舰导弹作为一种打击大型水面舰艇等时间敏感目标的精确制导武器,其初始条件、终端条件、威胁环境等轨迹优化基本条件,随战场攻防态势不同而各有不同.在实战条件下,它不仅要求轨迹生成算法的快速性,同时在弹道设计时必须综合考虑诸多实际约束条件,以实现安全飞行,并满足侦察、规避禁飞区等各种特殊作战需求.

再入反舰导弹滑翔弹头需要经历长时间大气内飞行,需要考虑其气动热、表面温度、过载、动压和控制裕度等作为轨迹优化的限制条件.

根据所获取的目标信息,满足基本再入生存条件,快速进行航路估算,根据所部署的再入反舰导弹机动能力,从能够覆盖待打击目标可能机动区的多种发射平台、多个发射阵地中,选择位置最佳的若干再入反舰导弹发射,以执行打击任务.最佳位置的判别,以最短射程、最小打击时间、目标机动区覆盖度最大等作为标准.

应尽可能根据侦察所获取的地基、海基拦截导弹等防空威胁区信息,规划绕过防空威胁区的飞行弹道.由于军事大国近年来大力发展海基导弹防御系统,其防御区域不断扩大,会出现部分防空威胁区无缝覆盖的情况,需要考虑根据其威胁度,规划防空威胁最小飞行弹道.而在防空威胁区范围内,应当根据所侦测到的威胁信息,进行有针对性的主动突防.

作为一种航程远、飞行区域大的航天+航空武器,其轨迹规划,还应考虑禁飞区规避问题,以避免在作战使用时,侵犯中立国家领空,引发不必要国际争端.

在这些限制条件下,再入反舰导弹的弹道优化是一个复杂的多约束多阶段优化问题.

2 弹道优化方法及软件的选择

再入反舰导弹弹道优化问题有如下特点:

1)运动方程形式复杂,控制变量隐含于运动方程.

2)再入轨迹对气动力控制变量高度敏感,在轨迹控制精确性和姿态控制精确性之间,需要进行权衡.

3)再入飞行过程中受热流密度、动压、过载所构成的再入走廊严格约束,再入轨迹的可行域限制在较为狭窄的范围内.

4)根据作战使用要求,需要满足防空区和禁飞区规避、经过路径点、饱和攻击终端约束等实际需要.

弹道优化的限制条件非常复杂,弹道优化问题难度较大.为此我们必须选择和发展一种行之有效的方法.目前大多数弹道优化的数值方法都可以归为间接法和直接法两种基本类型[10].

间接法主要用于参考轨道的离线优化,而对于RASM弹道生成这样的约束条件可能会随战术需求随时发生变化的实时轨迹优化应用场合,间接法则不太适用[11].

相对于间接法,直接法在收敛的鲁棒性和解决实际复杂问题的适应性上具有优势[12−13].直接法主要包括只离散控制变量和同时离散控制变量及状态变量两大类.然而,高超声速飞行器的轨迹对控制变量十分敏感,使直接法中仅离散控制变量的方法用于轨迹优化比较困难.尤其是对再入轨迹优化这类强非线性问题易陷入局部解甚至收敛到不可行解.同时,离散控制变量和状态变量的直接法将节点状态变量也作为设计变量,且将动力学微分方程约束转换为一组代数约束,在解决参数敏感问题上比只离散控制变量的直接法更具优势[14−17].对于配点法,确定适当的设计变量初值是一个难点.发展较为成熟的配点法采用分段多项式近似动力学状态变量,在航天器轨道优化问题上有较为广泛的应用.

近年来,离散控制变量和状态变量一类直接法中的伪谱方法,逐渐成为最优控制问题求解方法的研究热点.伪谱方法与一般配点法不同之处,在于利用全局插值多项式的有限基在一系列离散点上近似状态变量和控制变量,而不是采用分段多项式.从插值多项式的角度,伪谱法可称为全局方法,而用分段多项式近似的方法可称为局部方法.全局方法相对局部方法的优势是能够以较少的离散点数获得较高的精度,这使得它具有计算效率上的优势.对运动微分方程维数较高的情况,采用局部方法的设计变量数目可能是全局方法的几倍.而且,近期关于伪谱方法的大量研究表明,局部配点法可能既不是最精确的也不是计算效率最高的方法.在伪谱方法出现的初期,曾遭到质疑,即伪谱方法是否能像局部方法那样较容易地限制沿轨迹的最大误差.在这个问题上,全局方法取得了重要进展[18−19].若采用全局多项式作为近似基函数的配置方法,取适当的离散点和插值多项式,全局多项式近似的最大误差可以确定.

基于伪谱方法的轨迹优化问题可以转换为非线性规划问题,在本文的优化策略下,需求解多个非线性约束优化问题.本文采用基于序列二次规划(Sequential quadratic programming,SQP)算法的最优控制问题求解器:PROPT,该求解器包含在Tomlab软件中.

序列二次规划也称约束变尺度法,是处理非线性连续系统优化问题的最常用和鲁棒的算法之一,是求解非线性约束优化问题的一种有效方法,目前在非线性规划问题中得到广泛应用.与其他优化算法相比,SQP的优点在于收敛性好、计算效率高、边界搜索能力强,且能有效处理含约束问题,目前在轨道优化问题的直接法求解过程中普遍应用.但该算法需要给定优化参数的迭代初值,且初值的好坏直接影响算法性能.初值的适当选取,是算法应用需要解决的问题.

Tomlab源于20世纪90年代一个用于优化研究与教学的UNIX与PC机平台通用、开放、集成MATLAB编程环境.其开发目的主要是为了集成针对所有类型优化问题的处理器,使研究人员在Matlab环境下更方便地处理实际优化问题.因为可以在Matlab环境下使用,因此,编写脚本或者函数时,既可以利用Tomlab自带的求解器,也可以利用Matlab优化工具箱,还可以借助MEX文件交互的方式,使用Fortran或者C/C++等环境下的既有优化函数.

经过十几年的发展,Tomlab已经成为一个基于Matlab的、支持多种求解算法的通用编程框架,可以求解包括线性规划、二次规划、非线性规划、线性混合整数规划、非线性混合整数规划等几乎所有的优化问题.

3 到达指定目标点的最优弹道

反舰导弹可以用于反舰,也可以用于打击敌海军基地等固定目标.其高超声速再入阶段与大空域机动及末端能量管理段结束后,应到达预定位置,然后进行末端的目标搜索,并导引向目标.到达指定目标点的弹道优化仿真约束值如表1所示.

3.1 最小气动加热弹道

3.2 到达指定点的最长飞行时间弹道

到达指定目标点,依据所选择的弹道不同,所需的时间具有一定差异.首先来看最长飞行时间弹道.

以J=(tf)max为优化目标,约束条件如表1所示,仿真曲线如图2(a)和2(b)所示,得到的最长飞行时间为2650秒.从图中可以看到,该弹道较为平滑,过载、动压等均较小,总气动加热、热流密度峰值较最小气动加热弹道略大.

另外,从图2(a)的高度曲线中可以看出,这种时间最长最优弹道,分为初始下降段和拟平衡滑翔段2个主要不同阶段.初始下降段采用大攻角,而拟平衡滑翔段采用最大升阻比攻角进行滑翔.

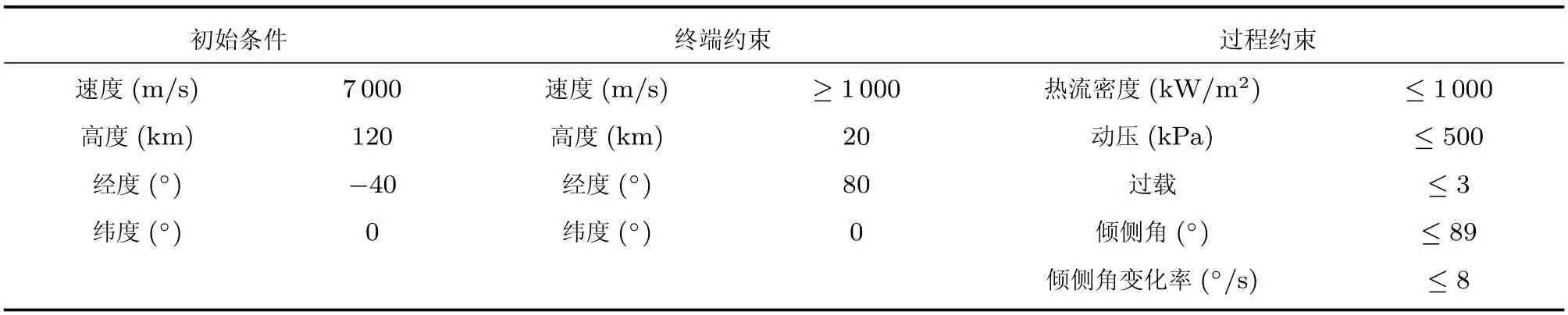
表1 到达指定目标点的弹道优化仿真约束值

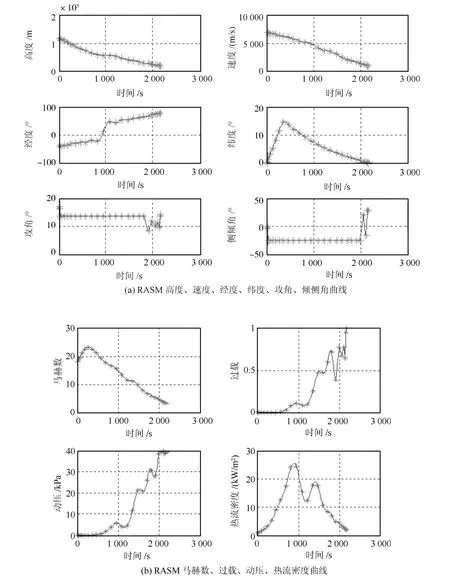
图1 最小气动加热优化弹道

3.3 到达指定点的最短飞行时间弹道

与此类似,以J=(tf)min为优化目标,约束条件如表1所示,仿真曲线如图3(a)和3(b)所示,得到最短飞行时间为2135秒.对比图2和图3,可以看到,最短飞行时间弹道中的飞行速度下降较为缓慢,因此飞行时间较短.同时,弹道的热流密度和动压峰值均较大,这说明,飞行时间最短与气动加热最小,这种目标某种程度上存在着一定的矛盾.如果需要进行多目标优化,则需要合理确定各子优化指标的加权系数.

4 饱和攻击最优弹道

由第2节中可以看到,到达指定目标点,依据所选择的弹道不同,所需的时间具有一定范围,对上面的算例,其时间范围为[2135,2650],这就为单基地、多基地先后发射多枚再入反舰导弹,对同一目标同时实施饱和攻击带来了可能.

本节提出一种优化策略,用于解决再入反舰导弹的攻击时间控制和攻击角度联合控制的多约束条件协同优化问题.思路是根据再入反舰导弹的飞行弹道特点,将复杂优化问题简化为一个约束条件和一个优化目标所构成的相对简单的优化问题.

图2 到达指定点的最长飞行时间弹道

首先,将角度约束作为终端约束条件:定义航向角ψh与相对目标点的视线角的偏差为∆ψh,为满足饱和攻击的角度控制需要,要求到达指定区域时的速度方向满足一定条件,即终端航向约束条件

以同一基地间隔T秒,先后发射N枚导弹为例.考虑饱和攻击的关键是同时到达,因此,首先在再入反舰导弹到达时间范围[tmin,tmax]内选择一个时间τ1作为第1枚导弹从发射到抵达目标点的时间,该时间作为再入反舰导弹的攻击时间控制和攻击角度联合控制的多约束条件协同优化的约束条件.则第i枚导弹抵达目标时间应为,τi=τ1−T(i−1),i=1,,N.

采用7枚弹演示多弹协同饱和攻击,取τ1=2540s,T=60s,∆ψhmax=5◦,到达目标点的期望航向角分别为∆ψhi=(105−15i)◦,进行多弹协同饱和攻击弹道的优化.其中,第4枚导弹τ4=2360s,ψh5=45◦的仿真曲线如图4(a)和4(b)所示.

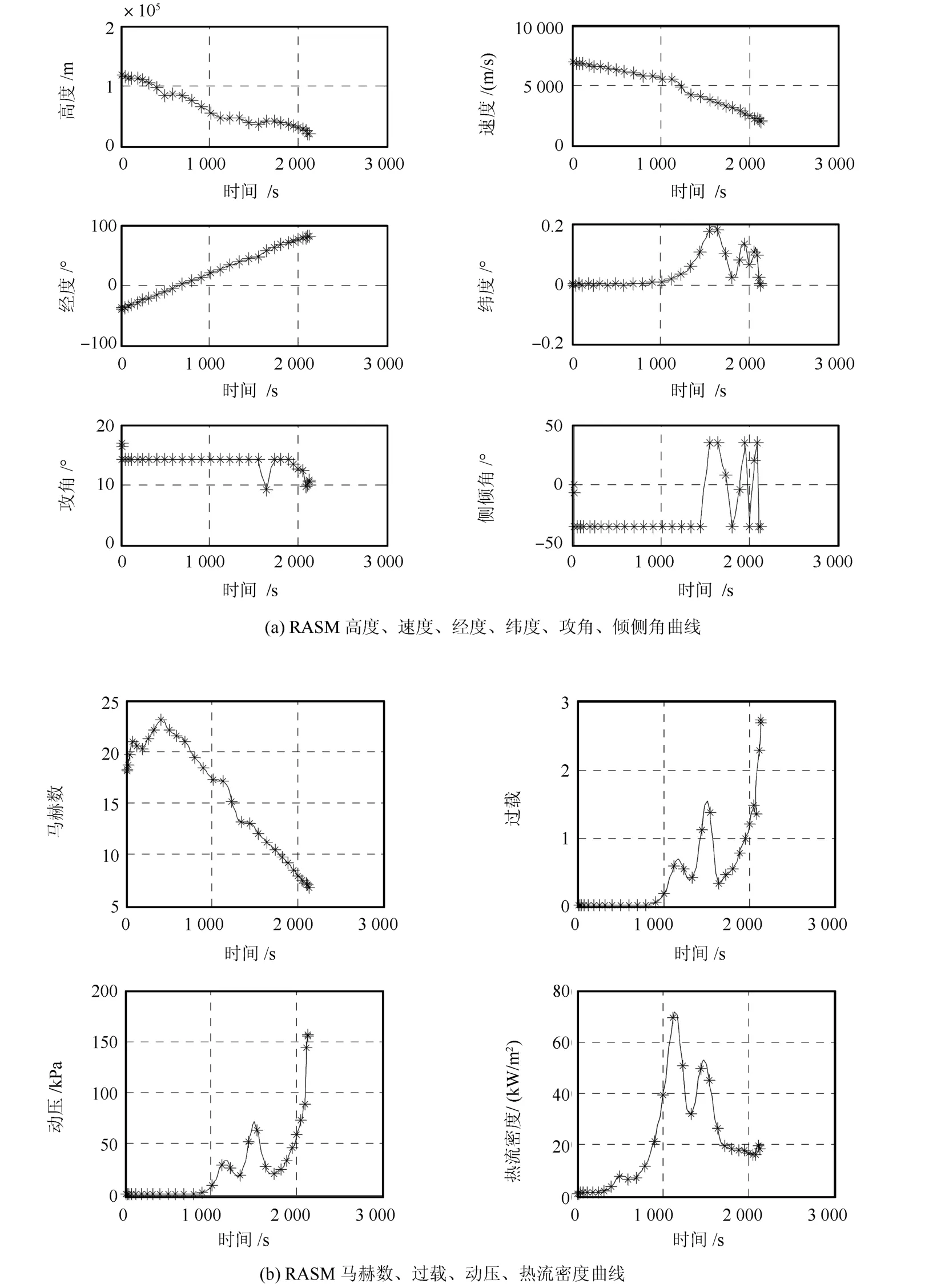
图3 到达指定点的最短飞行时间弹道

航向角随时间变化曲线如图5所示.从图中可以看出,航向角基本变化趋势是趋向于终端航向角,且变化率是越接近于目标越大,曲线就越陡峭.

多弹协同饱和攻击弹道优化误差数据如表2所示,到达目标点的实际到达时间与期望到达时间均在1秒以内;而攻击角度之差,均在5度以内,满足终端航向约束条件的要求.这验证了本节所提出的多弹协同饱和攻击弹道优化策略的有效性.

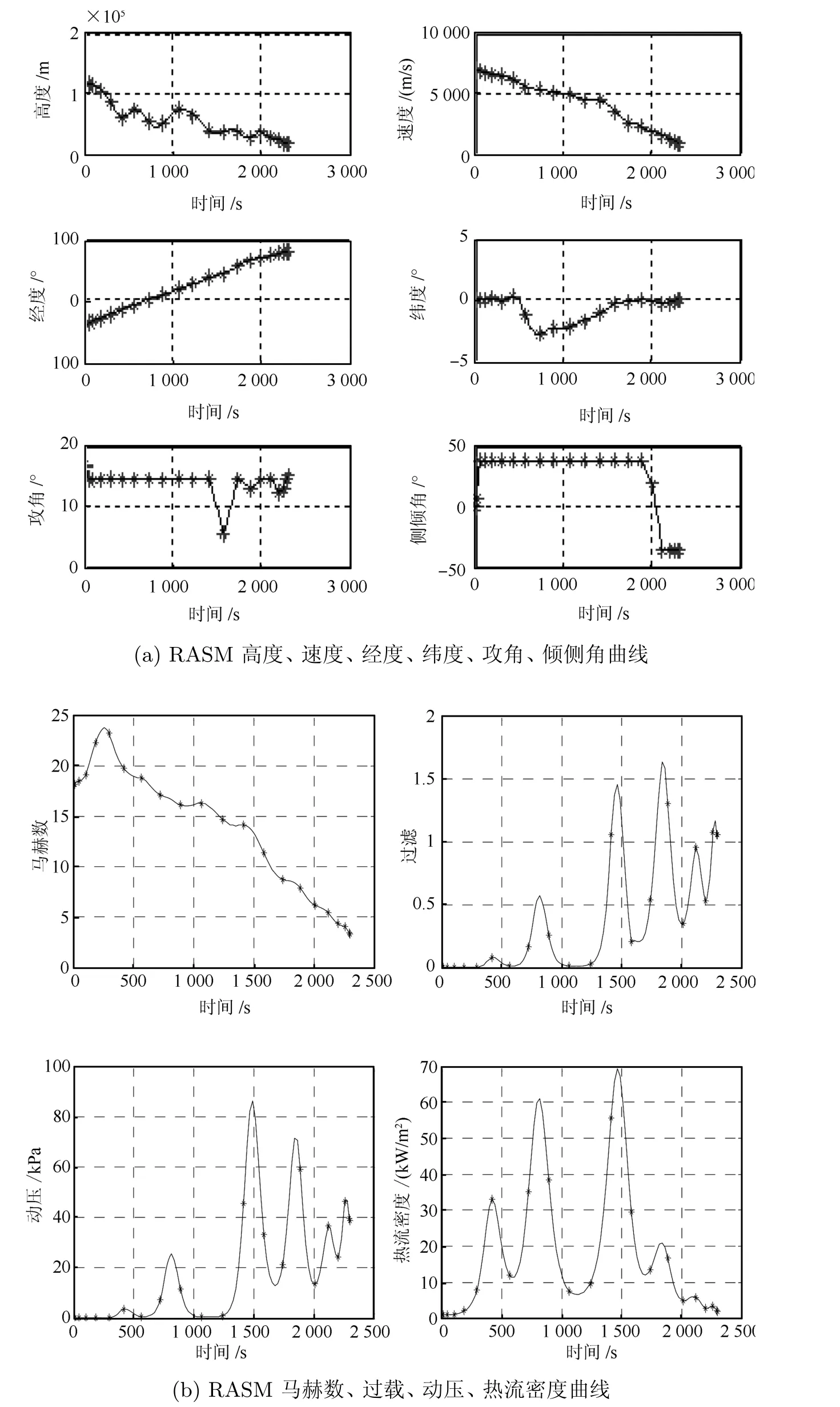
图4 攻击时间控制和攻击角度联合控制仿真曲线

仿真表明,采用第2节提出的弹道优化问题求解策略,在Intel Core2 Duo CPU L9600,主频2.13GHz;内存1.57GHz,3.0GB下,获得最优解的时间,一般均在1分钟以内.若采用PROPT的内置功能,将运行于Matlab环境下的优化函数转换为C++函数,则效率将可能会进一步提高.这显示本文所选用的优化软件,及RASM弹道优化问题特点与软件特点相结合所提出的弹道优化求解策略,具备离线及在线应用的潜力.

图5 多弹协同饱和攻击的航向角曲线

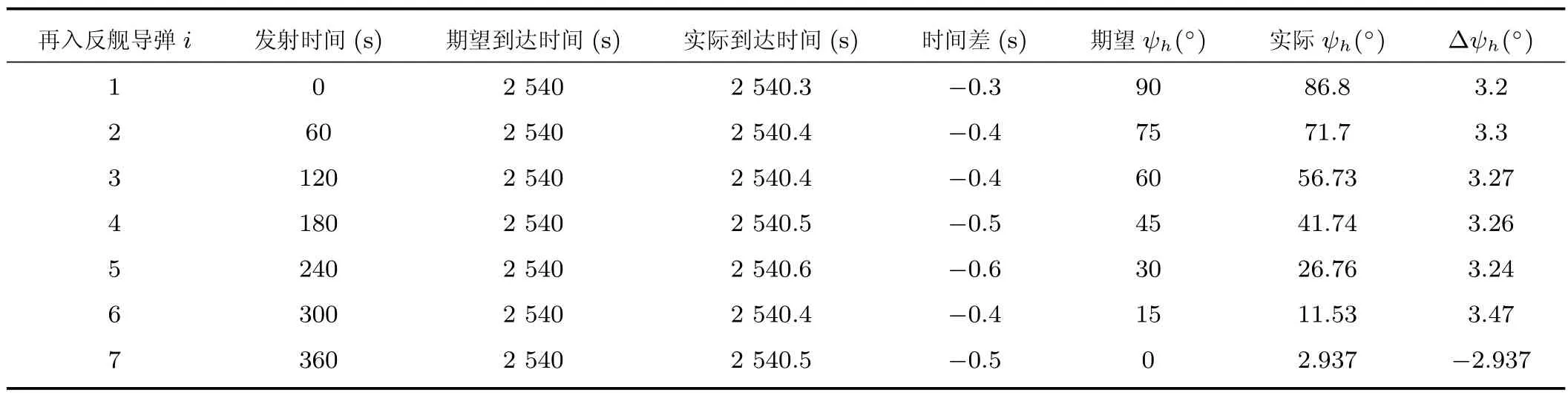
表2 多弹协同饱和攻击优化误差数据

大升阻比升力体反舰导弹再入时在初始下降段和滑翔段呈现出不同的特性,初始下降段弹道主要由再入条件决定,控制变量对该段弹道影响较小,滑翔段具有较大升力,可保持拟平衡滑翔状态,且弹道对气动力控制变量高度敏感.可以将再入过程分为初始下降段和滑翔段进行分阶段优化,这也可以方便地在PROPT中实现.

5 结论

本文分析了再入反舰导弹多弹协同饱和攻击突防弹道相关问题.从再入反舰导弹再入及应用约束条件分析出发,根据其特点选择了弹道优化方法及软件.通过弹道仿真,首先对到达指定目标点的多种最优弹道进行分析,建立饱和攻击最优弹道分析的基础.本文提出一种优化策略,用于解决再入反舰导弹的攻击时间控制和攻击角度联合控制的多约束条件协同优化问题.思路是根据再入反舰导弹的飞行弹道特点,将复杂优化问题简化为一个约束条件和一个优化目标所构成的相对简单的优化问题.所提出的多弹协同饱和攻击弹道优化策略有效性以及仿真软件的离线、在线应用能力均通过仿真进行了验证.