城市轨道交通系统的定价策略研究
——基于产品生命周期理论
韩冰冰,宋磊
(1.郑州市轨道交通有限公司,郑州450000;2.华北水利水电大学管理与经济学院,郑州450046)
城市轨道交通系统的定价策略研究
——基于产品生命周期理论
韩冰冰1,宋磊2
(1.郑州市轨道交通有限公司,郑州450000;2.华北水利水电大学管理与经济学院,郑州450046)
本文通过假定引入期和成熟期以“实现最优客流量”为首要目标,成长期和衰退期“以利润最大化”为首要目标,对城市轨道交通系统的各个时期分别建立模型来确定各个阶段的最优票价方案,以此来为运营公司确定合理的票价方案提供理论支撑。
城市轨道交通;票价制定;价格弹性曲线
0 引言
随着国民经济的迅速发展及人们生活水平的提高,现国内外各大城市交通规划以地铁为主体的城市轨道交通已经与常规交通一样扮演着重要的角色。国家为响应市场号召,于2003年出台了“国务院关于加强城市快速轨道交通建设管理的通知”,明确规范了申报发展地铁城市的“1313”门槛。
根据香港地铁公司收入的结构安排,票务收入是城市轨道交通系统运营过程中最稳定、最主要的收入来源,根据经济学中的弹性理论和城市轨道交通的服务特性,然后制定合理的票价以吸引足够多的客流量、获得足够的票务收入,必定是城市轨道交通系统良性运作的关键问题,这也是学术界和运营商都努力解决的热门问题。
1 理论简介
本文中主要根据产品的生命周期理论来确定轨道交通所处的阶段,然后从博弈论的视角来建立票价确定模型。故本部分主要介绍产品生命周期理论、博弈论和城市轨道交通特点3部分内容。
1.1产品生命周期理论
产品生命周期理论是美国哈佛大学教授雷蒙德·弗农(Raymond Vernon)于1960年在其著作《产品周期中的国际投资与国际贸易》一文中首次提出。将此理论应用到城市轨道交通系统提供服务的过程中,其4个时期的表现特征如表1所示。

表1 城市轨道交通各个时期的特征
从表1中可以看出,城市轨道交通的4个时期所经历的环境有所差异,如果我们用统一的模型来确定票价策略不可能合理,这就要求运营商要正确分析该系统所处的阶段,进而分析找出正确的模型。这也是本文从产品生命周期的角度来建立票价模型的主要原因。
1.2博弈论
博弈论是理性参与者在策略性环境中如何选择策略性行为的系统性研究。分析博弈论模型时主要考虑2个要素:2个或更多的参与者;2个或更多策略组成的策略集和支付矩阵。博弈的结果最终要找出一个各方都能接受的解,即纳什均衡解。因此,本文中所考虑的博弈均衡解为纳什均衡解。
1.3城市轨道交通系统的特点
充分认识城市轨道交通系统的特点,才有可能正确地确定票价模型,进而确定合理的票价方案。总结其特点主要有:第一,准公共物品性;第二,外部性;第三,政府主导性;第四,高峰期明显性;第五,强需求弹性。综合城市轨道交通系统的特点,其兴建时应该以政府为主导,运营期间不能仅仅考虑市场机制来确定票价,还要考虑其所带来的外部效应和规模经济,结合兴建城市轨道交通的初衷,制定合理票价的基本原则是:公益性优先,兼顾效率。
2 票价制定的博弈模型
结合轨道交通系统所处的阶段来确定票价策略时,考虑到不同阶段所追求的目标不同,不同时期的票价策略也应该有所不同,故应该合理地区分阶段来考察制定票价的模型。
2.1引入期
首先,当一个城市的轨道交通处于刚刚运营阶段,其首要目标应该是尽可能地增加客流量,并在充分发挥运能的前提下实现运营公司的收益最大化,同时还要充分考虑公众的承受能力以及常规交通系统可能的反映。
然后,以公交车系统为主体的常规交通能够为人们提供廉价的出行服务,尽管其所能达到的区域有所限制,但其廉价的服务获得了大众的青睐。此阶段的地铁网络仍未形成,如郑州地铁1号线只是贯穿市区东西向的一条线,市民利用该交通方式出行时能到达的区域很有局限性,吸引的主要是出发地或目的地在地铁沿线的乘客和好奇心强的乘客。此时,轨道交通与常规交通的竞争强度较弱,竞争范围也较小。
最后,分析模型。此阶段以追求收益最大化为目标,根据经济学原理,城市轨道交通的客流量(需求)与其自身价格和替代品(常规交通)的价格关系可以表示为:

式中:Q为城市轨道交通的客流量;Pg和Pc分别为城市轨道交通和常规交通的平均价格;α和β分别为城市轨道交通客流量对城市轨道交通和常规交通的价格弹性,且假设α和β与Pg和Pc都有关,且α<0,β<0。为方便期间假设,常规交通的平均价格水平不变,模型的问题化解为:

约束条件中,限制条件主要是价格和需求量水平的现实约束条件;解该模型时,首先对目标函数两边对数化得:
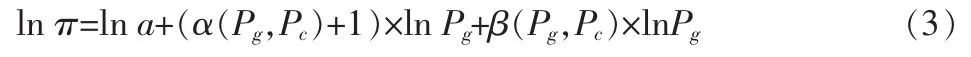
根据引入期的特点可以得出:此时常规交通的价格水平几乎不变,即可以假设为固定的常数。假设常规交通价格对城市轨道交通客流量的弹性β为:β=δPg,δ为正常数,即在增加轨道交通线路之前的引入期内,轨道交通价格对弹性β的影响固定不变。该模型的一阶条件(FOC)变为:


求解此常微分方程可得:
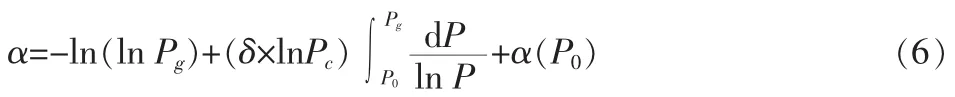
其中(P0,α(P0))为初始条件,式(6)中反应了票价和客流量价格弹性间的函数关系。根据引入期的目标(尽可能地扩大运载量),假设线路能实现最大运载量。结合式(1)和式(6)可得出最优的票价。
2.2成长期
第一,此阶段骨干线路基本建成,乘客可以不用几次换成就满足出行要求。此时的主要目标是保有并扩大市场占有率,实现利润(总收入-运营成本)最大化,以追求营运收入与营运费用相平衡。
第二,与引入期相比,常规交通的状态并没有明显的变化,而城市轨道交通对常规交通的依赖性下降,且与常规交通形成对立态势,两者间的竞争强度和范围都在不断增大。
第三,博弈过程中追求的目标变成了收益(指的是收入减去运营成本)最大化,此时考虑的博弈模型仍是非合作博弈。乘客出行方式的选择仍使用logit模型,该模型的表达式为:

式中:xi为乘客选择第i种交通工具的概率;Vi为乘客乘坐第i种交通工具的效用;n为可供乘客选择的交通工具种类,这里n为2。
为了方便起见,公式(7)中的Vi写成:

其中θ为矫正系数,其取值在区间[3,3.5]内。最终形式为:

其中,ψ是时间转化为货币价值的系数,其公式为:

式中:Ti为选用第i种出行方式出行时所花费的平均时间,主要包括步行至乘车地的时间、等待乘车时间、坐车时间、换乘时间及班车误点平均时间;Di为选用第i种出行方式的舒适度,货币计量方法是低峰期为票价的10%,高峰期为票价的5%;Pi为乘坐第i种出行方式时的票价;Qi为选择第i种出行方式机会成本的调整量。
设符号M为城市的总客流量,Mi为交通方式所承担的客流量,σi为交通方式i获得的政府总补贴,τi为交通方式i的边际成本,Fi为交通方式i的固定成本。故收益的表达式为:

该模型的求解仍然利用伯特兰—纳什均衡模型来求解,追求利益最大化的FOC为:(条件(7)、(8)是实际限制条件)

其中i=1,2,利用上述模型得出各种交通方式的最优票价方案,式(11)的结果是各个交通方式的反应函数,与引入期一样,共2个未知参数,2个独立的方程式,再依据限制条件(12)和(13),进而可以确定各个交通方式的定价策略。历史数据总结出城市的总客流量特征,将总客流量数据与选择轨道交通出行方式的概率相乘,即可得出轨道交通系统所运载的客流量。
2.3成熟期
第一,此阶段四通八达的轨道交通网络已经形成,居民的出行轨迹已固化在网络运营公司的规模,经济十分接近充分发挥,其战略目标变为提升运营效率,利用价格疏导客流,避免交通拥堵。
第二,常规交通系统与前两阶段的状态相比并无变化,而此时的轨道交通系统的线路网络已经很健全,规模经济和网络效应充分展现出来,其运营成本已经降到预期的低水平,其价格已经具备绝对优势,且此时的真实运载客流量已经实现或超过预期值。
第三,根据经济学原理可知,由于城市轨道交通系统在此阶段具有价格绝对优势,如果按照利润最大化的价格来制定票价,必定会带来轨道交通系统的客流拥挤,乘客的舒适度下降,一旦人们认识到乘坐轨道交通系统的这个问题,必将会转乘其他交通工具,如此以来势必会造成客流量的波动。
为避免客流量的波动,适当地提高城市轨道交通的平均票价,进而让客流量始终维持在城市轨道交通网络的最大运载能力。此时所选用的分析模型与引入期的模型相似,只是相应的参数发生了变化。
2.4衰退期
第一,尽管目前全球范围内并未出现衰退期的迹象,当衰退期显现时,随着科技的发展,或许将来的某个时期会出现这样的情况,此时城市轨道交通的运营商的战略目标变为:确保营运过程中的收支平衡,改进或转变所提供的出行方式。
第二,此时已经出现了新的更快捷、环保和可靠的交通方式,但该交通方式刚刚进入引入期,其规模经济仍不明显,对其他交通方式的依赖性也较大;而城市轨道交通仍可能具有价格方面的优势,低廉的价格仍能确保其能继续存在一定的时期。
第三,此阶段运营商又要重新考虑收支平衡的问题,即追求利润最大化的同时来维持收支平衡。此阶段的模型与成长期的模型相似,不同的是增加了新的交通方式,且旧交通方式不断推出市场导致其运载量会有所下降。其伯特兰—纳什均衡模型结果仍参照成长期的结果,只是增加了一个交通方式。
3 数值分析
本章对引入期模型做数值解,设参数Pc=2.3,δ=0.01,α=300000。日客流量Q=16.2万人次。其中,初始值条件为:当Pg0=2,α=-0.12时,通过式(6)可以得出城市轨道交通客流量对其票价的弹性与其价格的关系图如图1所示,其表达式为:
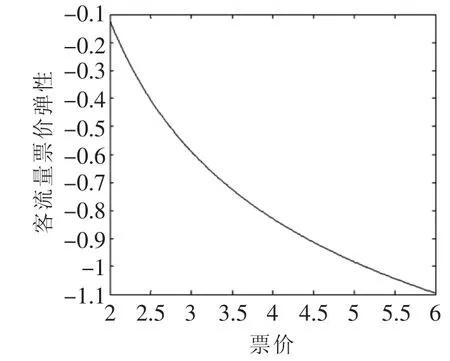
图1 城市轨道交通客流量票价弹性与其价格之间的关系
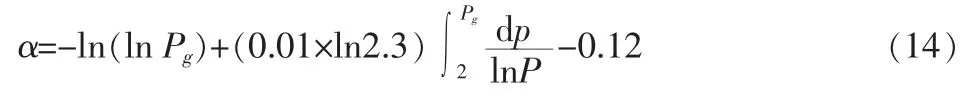
4 结论
城市轨道交通系统的特点决定着其票价水平应该充分考虑其竞争者的行为,而不能仅仅由运营商自主决定。通过本文对轨道交通票价制定的深入研究,可以得知:尽管轨道交通系统在各个时期的战略目标和竞争环境有很大的不同,城市轨道交通和常规交通的动态竞争关系仍可以用博弈论所构建的模型来描述和分析,通过此模型可得到更加合理的票价方案。文章最后对算法进行了数值分析,分析结果也验证了本文提出的观点的可行性。
主要参考文献
[1]陈翠利.基于生命周期的城市轨道交通合理票价分析[J].城市轨道交通研究,2012(5).
[2]高明远.地铁票价及改革策略初探[J].价格月刊,2014(11).
[3]王超,李凡.北京地铁票价与人均GDP及收入关系探究[J].发展研究,2014(12).
[4]邓东德.重庆城市轨道交通外部效应分析及评价指标体系研究[D].重庆:重庆交通大学,2013.
[5]蒋伟林.香港地铁系统票价弹性的研究[J].城市轨道交通研究,2006(11).
[6]谭家美,王正.基于隐类模型的轨道交通票价分级制定[J].城市轨道交通研究,2013(7).
[7]秦华容,杨铭,米雪玉.基于缓解拥堵目标的城市轨道交通定价策略[J].价格月刊,2013(8).
[8]周苗雨,王守彬.基于城市轨道交通与常规交通竞争的票价制定模型[J].交通与运输:学术版,2014(1).
10.3969/j.issn.1673-0194.2015.15.061
F505
A
1673-0194(2015)15-0110-04
2015-06-03

