有交易费和随机分红的多因素期权定价模型

秦浩洋 杨泽霖 庞睿康

(1.3.西安交通大学数学与统计学院，陕西 西安 710049;2.西安交通大学金禾经济研究中心，陕西 西安 710049)

一、经典Black-Scholes期权定价模型

期权是一种特殊的金融衍生品，它赋予持有人在特定时期以确定的价格买入或卖出一种标的资产的权利。看涨期权是以某一确定的价格买入一项资产的权利;看跌期权是以某一确定的价格卖出一项资产的权利。期权执行的日期叫到期日;期权执行时支付给标的资产的价格叫做执行价格。美式期权可在到期日之前任何时间执行，欧式期权只能在到期日执行。

为推导Black-Scholes期权定价模型，作以下假设:

①标的资产的价格S遵循布朗运动，即S满足dS=μSdt+δSdz，其中是一个维纳过程，满足;②在期权的有效期内无风险利率r和标的资产价格S的波动方差率是时间的已知函数;③套期保值没有交易成本;④满足无套利原理，无风险利率为r;⑤在期权的有效期内不支付红利;⑥标的资产可以连续交易;⑦允许卖空，资产可以细分。

假设是基于S的欧式看涨期权价格，由ITO引理可以得到:

构造一个包含f(S，t)和S在内的投资组合，这个投资组合的持有者卖空一份价格为f(S，t)的期权，买入数量为的股票(这个数量的确定方法将在下文给出)。此时该投资组合的价格为

将式子的两边对t求微分，得到

将以上各式带入可得到

利用无套利原理，可以得到

带入上式即得到经典的B-S模型

边界条件为c=max(Sr-E，0)

这是一个热传导方程，利用fourier变换可以求得其解析解

c=SN(d1)-Ee-r(T-t)N(d2)

其中，N(*)表示均值为0，标准差为1的标准正态分布分布函数，其中

由于方程中不含有投资者的风险偏好量μ，故在期权定价中，可以采取任意一种风险偏好(一般采用中性风险偏好)，这是B-S模型的一个重要性质

最后，我们来说明投资组合Π的确定方式，利用待定系数法:假定我们的投资组合为卖空一份价格为f(S，t)的期权，买入a份价格为S的股票(a为待定常数)，那么该投资组合的价值为

Π=-f+aS

同样在等式两边对t求微分，并带入以上各式，得到

然而根据无套利原理，在无风险利率确定的情况下，dΠ是一个确定量，所以当中不能含有随即项dS，所以只有

至此，我们回顾了经典的B-S模型的推导，并对其中投资组合的构造方法做了更进一步的讨论。基于此，在下一个部分中，我们将给出多个标的B-S模型的推导。

二、多因素期权定价模型

为了推导γ1维Black-Scholes期权定价模型，首先证明如下定理。

定理γ1维伊藤引理

设随机过程{xk(t)，t＞0，k=1，2，…，n}循伊藤过程

dxk=ak(x1，x2，…，xn，t)dt+bk(x1，x2，…，xn，t)dzk，k=1，2，…，n

其中dzk是一个标准维纳过程，设G=G(x1，x2，…，xn，t)是x1，x2，…，xn，t的函数，连续可微，则G满足:

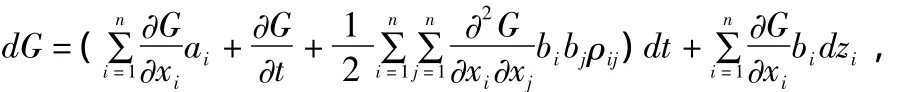
其中ρij是xi，xj之间的相关系数。

证明:设zk=εk，εk～N(0，1)，则εi，εj的相关系数为ρij。由多元函数的Taylor公式，有

由

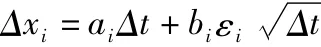
得:

又

当Δt→0时，

Var(εiεjΔt)=o(Δt)→0

于是εiεjΔt可看作非随机变量，并且等于数学期望，此时

ΔxiΔxj= ρijbibjΔt+o(Δt)

代入得

令Δt→0且将dxi=aidt+bidzi代入得

设第i种股票价格为SI，满足dSi=μiSidt+σiSidzi，

且dzidzj=ρijdt

则对期权价格f，有下式:

将dSi=μiSidt+σiSidzi代入得

构造一个包含f=f(S1，S2，L，Sn)和S1，S2，L，Sn在内的投资组合，即卖空一份股票，买入数量为的股票(购买价格为Si的股票份)。则该投资组合的价值为

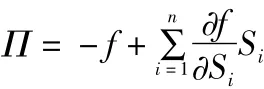
这里的Π的确定方法与一维经典B-S模型推导中的方法一样。对上式等式两边求微分，

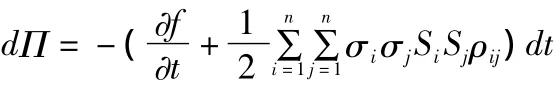
结合无套利原理，有dΠ=rΠdt

带入上式即可得到n因素的期权定价模型

边界条件为

cT=max(S1T，S2T，L，SnT，E)-E

对于该方程，当n=1时，即是经典的B-S模型，我们可以很容易求出其解析解;当n=2时，该方程的解析解也可以得到，其解析解为

cT=S1T［N(d1)-N2(-d1，d3;ρ1)］+S2T［N(d2)-N2(-d2，d4;ρ2)］+Ee-r(T-1)［N2(-d1+σ1(T-t)1/2，-d2+σ2(T-t)1/2;ρ)］-Ee-r(T-t)

其中

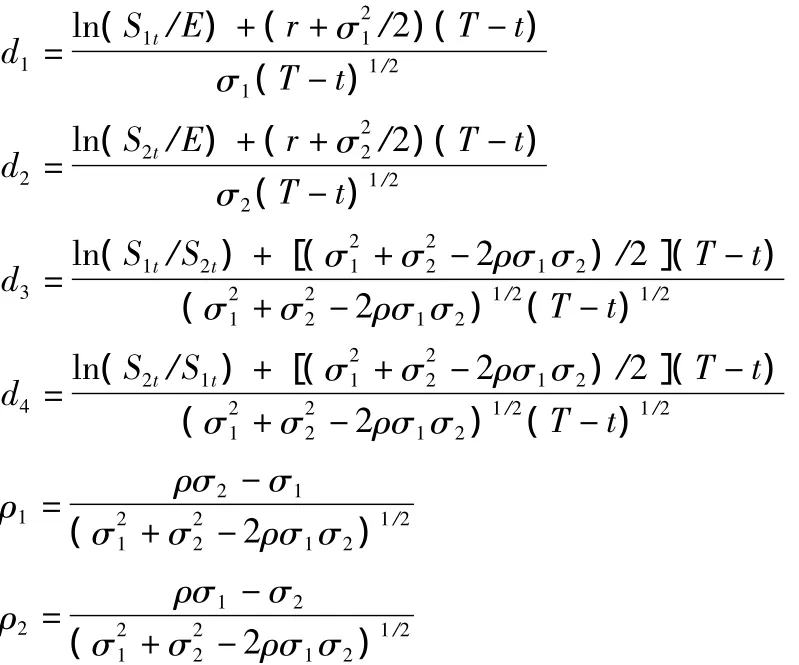
N(*)和N2(*)分别为一维和二维的标准正态分布函数;对于n＞2的情况，一般难以做出其解析解，所以可以采用数值的方法进行求解。

三、考虑有交易费和随机分红的情况

市场上股票的的交易有买入和卖出的费用，买卖的交易费率分别为λ和μ(0≤λ＜1，0≤λ＜1)。即购买价格为s的v股股票，现金支出为(1+λ)sv，出售价格为s的v股股票，现金获取为(1-λ)sv。

一份彩虹期权的标的为n股股票s=(s1，s2，…，sn)，股=(，，…，)，D票分别在ττ1τ2τn时间随机分红分红的红利为

=(d1，d2，…，dn)。

彩虹期权在T时刻交割.

投资者选择自己的买入和卖出的策略集为{L(t)，M(t)}，是一组F-适应的，右连续，非减过程。L(t)表示在t时刻买入L(t)=L(t)份额的股票，M(t)表示在t时刻卖出M(t)份额的股票。

作为理性的投资者，选择的交易策略应该是有能力偿付的策略。定义有偿付能力的空间V={(s，x，y)∈Rn+×R1×RYLn+，M|)x∈+(V1，则+称λ)该sT交y≥易0策，x略+是(1可-行μ)的sT。y≥0}。若(S(t)，XL，M，

当投资者选择了可行的交易策略{L(t)，M(t)}后，持有股票的份额服从过程为dY(t)=dL(t)-dM(t)，财富变化为W(t)=XL，M(t)+YL，M×s(t)。彩虹

假期定权投，即资为者W的0初=(始1财+富λ)恰(s好1+购s2买+一…份+含sn有)。n显种然标，的将的所有财富

先购观买察为其一中份的彩一虹只期标权的是

s。可行的策略。

1

假定基于现有的信息集Ft上，未来时刻的分红的现值Dτ是可以被无偏估计的，即Dτ=E［Dτ|Ft］e-r(τ-t)，等式中r为无风险利率。

设为了推导出有随机分红项的股票现值，设置标的资产为τ时刻的分红的远期合约。合约敲定时，空头和多头商定在τ时刻多头支付给空头FD(t，τ)，而多头持有者获得股票的红利［D|F］。根据有效市场假定，不存在无风险逃离的

τt情况，即分红远期合约的现值应该等于，未来时刻的分红的现值D无偏估计。

τFD(t，τ)=Dτe-r(τ-t)(*)

在初始时刻，空头(1+λ)s买入一股股票。到时刻，多

1头获得红利Dτ，空头获得合约交割价FD(t，τ)，并将这部分。钱购买无风险资产

到T时刻，空头交出股票，获得F(t，τ)的合约价(加上交易费后实际获得(1-μ)F(t，τ))。则空头的总收益为(1-μ)F(t，τ)+FD(t，τ)er(T-τ)。根据无套利原理，应该等于其初始的现值(1-μ)F(t，τ)+FD(t，τ)er(T-τ)=(1+λ)s1(t)

带入(*)有

(1-μ)F(t，τ)+Dτe-r(τ-t)er(T-τ)=(1+λ)s1(t)

解得

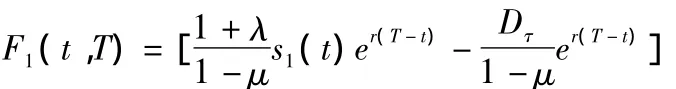
即彩虹期权中每一只标的股票在现有信息集下随机分红后的估计应该是

最后，我们只需要把n维B-S公式中的Si替换成Fi，即可得到有交易费和随机分红下彩虹期权的定价公式:

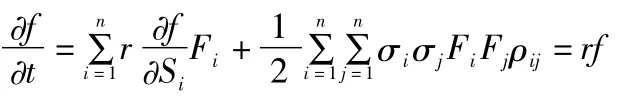
其中

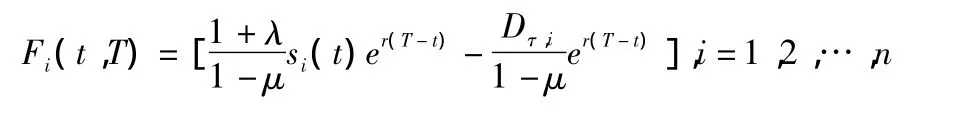
当n=1时，此时的多因素期权与一般的期权相同，其定价公式变为:

其中，N(*)表示均值为0，标准差为1的标准正态分布分布函数，其中

当n=2时，其定价公式为

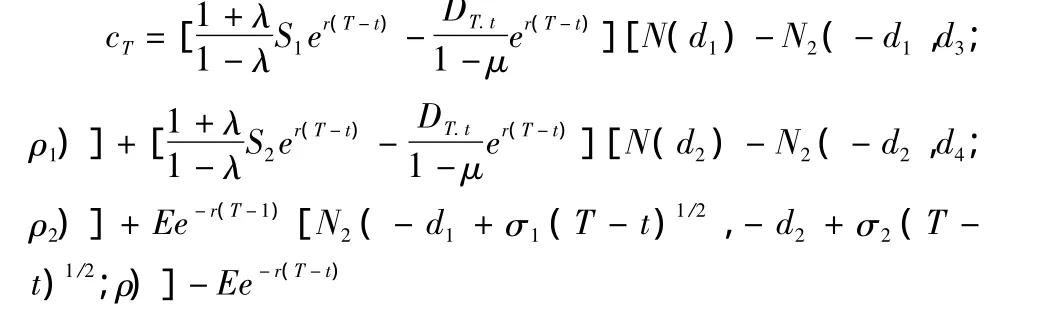
其中

N(*)和N2(*)分别为一维和二维的标准正态分布函数。

对于N＞2的情况，我们只能求出其数值解，这已经超出了本文的内容，不再讨论。

［1］吴永红.蹇明.叶小青有交易费和随机分红时的欧式期版权)，定20价05［，3期3(刊6论)文］-华中科技大学学报(自然科学

［2］吴云.何建敏 多 因素型期权定价模型的研究［期刊论文］-东南大学学报(自然科学版)，2002，32(1)

［3］汪北昌京云，20金13融.衍生工具(第二版)中国人名大学出版社，

［4］Joseph Stampfli.Victor Goodman(著)，蔡明超(译)金融数学机械工业出版社，北京，2004.