在活动中感悟思想、积累经验

钱建兵

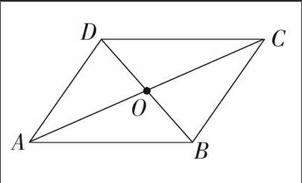
苏教版五上P15“动手做”。

在方格纸上画平行四边形ABCD，连接对角线AC、BD，它们的交点O称为平行四边形的中心。

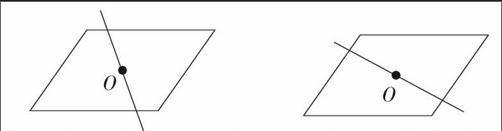
过平行四边形的中心O任意画一条直线，把平行四边形分成了两个什么图形？这两个图形完全一样吗？先画一画，再把分成的两个图形剪下来比一比。

你能用上面的方法把下面这些图形分成完全一样的两部分吗？先画一画，再与同学交流。

【教学片段一】

出示一些平面图形：正方形、长方形、平行四边形、正六边形、正八边形。

师：这些图形认识吗？六边形特别吗？每条边都相等、每个角都相等的叫正六边形。

师：今天我们要学习这些图形的分割。

师：你能在这个正六边形上划一条直线，将它分成面积相等的两部分吗？

生■：在中间画一条。

师：有多少种画法？

学生大都表示有4种，也有学生表示有6种。过了一会儿，有一两位学生表示有无数种。

师：碰到复杂的问题可以从简单的问题入手，你们觉得可以从哪个简单的图形入手？

生■：正方形。因为正方形的边少。

师：可是长方形也只有4条边啊？

生■：正方形不仅边比较少，而且跟正六边形相似，每边都相等的。

【赏析】教师没有直接出示正方形让学生研究，而是故意将题目变复杂，“难为”一下学生。这种“颠倒法”产生的冲突，实际上是在向学生巧妙地渗透“从简单想起”的数学思想。数学思想的基本教学形式是渗透，是师生间谈话中的自然流露。“复杂的问题从简单想起”，实际上是一种类比推理，是合情推理。“长方形也只有4条边啊”很自然地将学生的视角引向类比的关键：两事物之间必须有相同或相似的属性，相似程度越高，推理的可信度就越高。

【教学片段二】

师：正方形上画一条直线将它分成面积相等的两部分，这样的直线有几条？请大家拿出正方形，折一折，画一画。

学生操作，教师找不同的方法加以展示。

生■：上下对折，完全重合，再左右对折，再对角对折。

师：看一看这4条，这4条虽然来自四面八方，但都——

生■：相交于中间的点。

师：我们把这样的点叫中心点，在做的过程中我们有了新的发现。

生■：可以分成两个梯形，这个梯形少的部分（指梯形的上底），在另一个梯形中也有，多的部分（指梯形的下底），在那个里也有。这样两个梯形就一样了。

生■：这条不是随便画的，是围绕中心点画的。

师：只要找到怎样的直线，就可以将这个正方形分成相等的两部分？

生■：我感觉只要通过中心点，就可以了。

师：这位同学有很好的感觉，但我们还需要验证。

生■：可以剪开分成两份，看能不能重合。

学生操作，经过中心点任意画一条直线，可以剪，也可以测量。

师：我看到了两种不同的验证方法，一种是经过中心点，有意地画一条不一定就能确定的直线再剪开，另一种是沿对折的折痕剪开，你更欣赏哪一种？

生■：第一种，因为第二种不需要验证了。

……

师：一开始都认为是4条，尝试的过程中发现相交于同一个点，有部分同学有了大胆的猜想，我们就进行了验证，最后发现了这个结论。

【赏析】大部分学生都知道“正方形中有4条直线能将它分成相等的两部分”，基于对这一学情的把握，教师及时地将这种经验进行提升，引导学生发现问题的关键——都相交于中心点。当学生凭直觉发现其他的经过中心点的直线可能也可以将正方形平均分成面积相等的两部分时，进行验证的想法自然产生。学生在此感受到“猜想—验证”的探究过程。在这个过程中，教师的做法到位，但不越位，重视方法的指导，特别是验证的方法对学生的适当启发。

【教学片段三】

师：长方形呢？平行四边形呢？

师：这些想法是对的吗？是的，还需要科学的验证。你准备怎么研究？

生■：先找中心。

师：为什么不从头开始？是的，我们经常是借鉴之前的规律进行新的研究。

学生操作后交流。

师：研究到这儿，我们似乎找到了规律，借助这样的研究，我们来看一开始的那个问题，正六边形能有多少条将它分成相等的两部分的直线？

生■：无数条。这无数条直线都经过中心点。

教师课件演示。

师：正八边形，正二十边形呢？你想说什么？

生■：我感觉只要有中心点的图形都有无数条将它分成相等两部分的直线。

生■：我觉得三角形不可以。普通的三角形不可以，直角三角形不可以。

生■：等边三角形也没有无数条。

师：同学们有这么多猜想与追问，把掌声送给大家！

师：在研究数学的过程中，最重要的是我们要学会数学的思考。在研究过程中，对自己已有的结论产生新的猜想，这是非常可贵的。既然有了猜想与疑问就需要验证，我给大家准备了一个正三角形，还准备了一个正五边形。跟同桌一起想，有没有直线能将它分成面积相等的两部分，如果能，有多少条？把你找到的画出来。

生■：正三角形找到了3条。找到中心点，随便画了经过中心点的一条线，结果发现不相等。

生■：经过正五边形的中心点，只有5条能将它分成面积相等的两部分的直线。

生■：每个图形不都是有无数条将它分成相等两部分的直线。

生■：我发现了一规律，边数是双数的正多边形，有无数条将它分成相等两部分的直线，边数是单数的没有无数条。

生■：圆没有角，也有无数条的。

师：大家都有了新发现，这个发现是不是成立，还需要验证。

【赏析】学生经历了研究正方形、长方形、平行四边形的过程，积累了确定中心点的经验。正八边形、正二十边形的出现，以及相关的操作、验证，进一步强化了“只要经过这个图形的中心点的直线就可以将这个图形分为面积相等的两部分”的结论。同时，这些素材的出现，也是促使学生产生新猜想的因子——“是不是所有的图形都有无数条将它分成相等两部分的直线”。此前，学生经历了猜想与验证的过程，自然地想到要进行验证，很快地发现这个猜想的缺陷，继而又完善猜想。整个过程，教师给学生的空间很大，问题由学生提，方法也由学生想。学生积累了经验，收获了方法，课堂得以延伸。

【笔者感悟】

1.规律重要，但方法更重要。

数学教学，让学生掌握知识、形成技能、发现规律，这固然重要，更重要的则是让学生知道怎么研究这些规律。正如课的最后，庄老师引用毕达哥拉斯的话：“在数学的世界里，重要的不是我们已经知道什么，重要的是我们是怎么知道什么的。”本节课，庄老师站在让儿童学会数学的思考的角度，把握整个教学，让学生经历了观察、尝试、猜想、验证，并得出结论的过程。最后，当学生以为规律要尘埃落定时，又产生新的疑问：“所有的图形都有无数条将它分成相等两部分的直线吗？”再次地反思、验证，向学生展示了探索规律的方法与路径——不断地猜想、验证、质疑、完善。学生收获的是思想方法，数学的活动经验在操作与交流反思中积累与沉淀。

2.教师要有课程意识。

数学不只有枯燥和呆板的一面，数学是生动与丰富的。儿童数学课是实践活动课程，在活动中有数学思维的生长，数学思想的渗透、活动经验的积累需要在“做”的过程和“思考”的过程中积淀。数学的世界有大量的素材，因此，教师应有课程开发意识，建立大数学教育观。只有这样，才能成为一个真正意义上的数学教师，是一位体现了数学、具有数学教育眼光并身体力行的人。在学生的世界里，数学教师就是数学。

（作者单位：江苏省南通市通州区西亭小学 责任编辑：王彬）endprint