基于BP和RBF神经网络的水轮机综合特性曲线的拟合
黄山
(吉林省水利水电勘测设计研究院,吉林长春130021)
基于BP和RBF神经网络的水轮机综合特性曲线的拟合
黄山
(吉林省水利水电勘测设计研究院,吉林长春130021)
关于大波动过渡过程中水轮机特性曲线的处理有很多种方法,其中有用神经网络方法来训练相关数据形成网络从而预测待求数据点,其中BP和RBF两种网络为较为常用的神经网络方法。本文通过学习Matlab中神经网络工具箱的调用,比较分析了BP和RBF两种神经网络在水轮机特性曲线拟合上的区别,试图找出BP网络隐含层神经元个数对其拟合精度的影响,以及随着其神经元个数增加而拟合度增加的情况。
BP与RBF神经网络;数据拟合;综合特性曲线;水轮机
0 引言
由于输水道和调压室结构参数、水轮发电机组参数、导叶关闭规律等的选择都将受到输水系统水锤波的严重影响,而水电站大波动过渡过程数值计算可以很好地模拟瞬变流过渡过程中水锤波对整个输水系统的主要作用,因此水电站设计较大程度上将受到水电站大波动过渡过程数值计算分析结果的影响。同时,该计算分析结果也为水轮机机组的安全稳定运行提供了可靠的前提条件。在水轮机调节系统大波动过渡过程计算中,需要知道水轮机的流量特性和力矩特性。而这两种特性往往是根据厂家提供的模型综合特性曲线和飞逸特性曲线转换获得。但综合特性曲线只提供高效率区附近的特性,而飞逸特性只提供空载工况的特性,这只能提供过渡过程计算中流量变化区域内一小部分的水轮机特性值,是远远不够的。因此,对水轮机综合特性曲线的数据进行处理是开展水电站过渡过程数值计算前期的基础性工作之一,从而求解出其在各个工况下(特别是在小开度和转速时)的流量和力矩特性。
对水轮机模型综合特性曲线进行处理从而获取相应信息的方法有好几种。例如,传统的人工经验延伸法、最小二乘法拟合、二次或三次样条插值法、人工神经网络等方法。人工经验延伸方法是依据已有的特性曲线区间,以飞逸特性曲线及其它边界限制条件作为限制点,依据经验对综合特性曲线进行延伸,使得整个延伸后的曲线满足基本条件且光滑平顺即可。由于完全依靠人工经验,所以较难把握。而最小二乘法拟合、二次或三次样条插值法、人工神经网络等方法则将综合特性曲线以相应的数学方法借助数学工具,在限定的边界条件下做相应的扩展延伸,使得延伸难度有所降低。其中用人工神经网络处理综合特性曲线的方法由于神经网络本身模型的不同,又有很多种类。本文仅仅针对BP神经网络和RBF(径向基神经网络)神经网络这2种不同的人工神经网络对水轮机综合特性曲线延伸、处理结果进行比较和探讨。
BP神经网络是一种利用误差反向传播训练算法的神经网络,是一种有隐含层的多层前馈神经网络,系统地解决了多层网络中隐含层单元连接权的学习问题[1];RBF神经网络由3层组成,这种网络具有较高的局部逼近能力,所以,径向基函数网络也被称为局部感知场网络[2],RBF神经网络的输出为隐层节点输出的线性组合。
1 相关工作
1.1建立BP与RBF网络模型计算验证
首先建立BP神经网络模型,由于前人已经证明一个单隐层三层的前馈型人工神经网络,在隐层节点足够多的情况下,经充分学习,可以任意精度逼近任何非线性函数[3],所以先建立了一个单隐层网络(输入层,1层隐含层,输出层),其中隐含层采用Sigmoid(S)传递函数。但由于隐含层神经元个数不能确定,只能从1个开始,个数一个个地增加,同时观察误差值是否达到所需精度。
Matlab中RBF有“newrbe”和“newrb”两种方式可供调用,前者隐含层神经元个数固定,后者需要手动调试确定神经元个数。作者经计算比较后于本文选用隐含层神经元个数固定的“newrbe”进行建模分析。
1.2发现现象
在BP和RBF两种神经网络模型计算过程中,发现BP网络隐含层“最佳神经元个数”很难确定,同时在隐含层神经元个数增至一定大小后,训练输入的误差精度提高非常缓慢,甚至随神经元个数增加而呈波浪状摆动。而RBF采用固定神经元方式,所达到的误差精度非常高,这两者有着明显的区别。所以先尝试提高BP神经网络的误差精度,看在隐含层神经元个数增加到多大时,能达到跟RBF固定神经元个数方法下一样的精度值。
1.3尝试找出问题所在
在解决上一节的问题时发现,在相同的隐含层神经元个数下,训练过程是变动的,并且最终达到的精度级别也有区别。经过查寻相关资料发现:matlab神经网络工具箱中每次对神经网络进行训练时都是随机产生的初始值,目的是为防止误将网络局部最优值作为全局最优值。因此本文计算采取在隐含层神经元个数固定的情况下,分别训练20组(即随机取20个不同的初始值用以训练网络),然后取误差值最小的那一组训练成的网络作为该神经元个数下对应的相应网络。同时,由于最后关注的是水轮机特性曲线节点值(训练输出值)与网络训练节点预测值误差程度,故将该差值最小的那一组选做20组训练网络中的最佳网络。在训练过程中,由于隐含层神经元个数一个一个增加,训练非常缓慢,因此编制小程序以方便计算和最终提取计算结果。
2 算例
2.1算例简介
采用A179-40模型转轮综合特性曲线来进行计算验证。算例从中共取了31×16=496个数据点,16为开度点个数,31为单位转速个数。
2.1.1水轮机特性函数描述
水轮机主动力矩Mt和流量Q的变化特性即为水轮机的静态特性,混流式、轴流定浆式水轮机的力矩和流量的函数表达为:
Mt=Mt(H,α,n)Q=Q(H,α,h)
式中:H为水头;n为转速;α为导叶开度。
水电站大波动过渡过程前处理的是模型综合特性曲线,该曲线是指模型水头为1m时对应的开度、转速和流量的关系,或者和效率的关系。因此换算后的力矩力量特性函数表达式为:
Mt=Mt(α,h)Q=Q(α,h)
因此在神经网络模型中,开度α和转速n为训练输入值(2维向量),水轮机主动力矩Mt和流量Q为训练目标输出向量。本文中以流量Q为目标输出向量作为例子来建立水轮机特性相应的神经网络模型。
2.1.2归一化处理
输入学习的样本各值之间往往存在着量纲、数量级不同等方面的问题,有时各数值之间相差较大,因此需对神经网络的输入输出数据进行一定的预处理,预处理的方法主要有归一化处理和标准化处理,当网络输入和目标矢量的取值为[-1,1]时,可以达到最好的效果,因此该算例在对网络进行训练之前预先对样本数据作归一化处理。
2.2BP神经网络建模
2.2.1水轮机特性建模
利用BP神经网络L-M算法模拟水轮机的特性数据,网络结构采用单隐层前向网络见图1,其输入层和输出层单元为线性神经元结构,隐含层采用双曲正切型sigmoid传递函数(matlab内部调用参数为“tansig”),其输出范围为[-1,1]。人工神经网络理论证明,这种网络结构能在任意给定精度下逼近任何给定的连续函数。理论上,BP神经网络的隐含层节点数只要越多,其所能达到的精度也将越高,但与此同时也将增加网络权值的训练时间[3]。为了研究含有不同隐含层节点数的BP网络与样本数据的逼近能力,本文以案例中提供的水轮机综合特性流量曲线处理数据为样本,对隐含层节点数与网络逼近程度的关系进行了计算,选取误差精度10-12为收敛准则,当隐含层节点数取为15时,隐含层神经元个数最小,同时与样本数据的逼近精度很高(相比后面的逼近程度)。

图1BP“3层”神经网络
2.2.2计算结果
分别对3层BP神经网络隐含层个数从1到100进行100个网络的训练,每个网络选取20组随机初始值进行训练,将训练网络进行预测;当20组初始值相应训练出来的网络中,有一组预测结果与训练数据的输出值最大差值最小时,即将该组训练完成的网络作为该神经元个数相应条件下的神经网络。图2,3给出了网络预测值与实际训练值最大差值随网络隐含层神经元个数(从1~100)的变化规律(图2),及局部变化趋势(图3)。误差精度选取10-12是由于RBF模型直接预测结果与训练值差值即为10-12,因此就将其作为目标控制精度。

图2 隐含层神经元个数与拟合精度关系图

图3 隐含层神经元个数与拟合精度局部关系图
2.3RBF神经网络建模
将已提取的数据点作为样本点,确定输入样本值和目标值,建立一个RBF神经网络。经调试后,选择适当的均方误差参数GOAL值和径向基函数分布参数SPREAD值,利用MATLAB软件中神经网络工具箱内的函数 newrb(P,T,GOAL,SPREAD)建立并培训网络,进而即可完成水轮机综合特性曲面的拟合。RBF神经网络的学习过程分为两个阶段:第一阶段,根据所有的输入样本决定隐层各节点的高斯基函数中心值和标准化常数;第二阶段,在选定隐层参数后,根据样本,利用最小二乘原则,求出输出层的权值,然后,依据样本信号,再对隐层和输出层的参数进行校正,以进一步提高网络的逼近精度。前述过程可通过matlab神经网络工具箱中的“newrb”函数而实现。但尝试计算发现,神经元最佳个数需要一直增加,且很大,因此选用了其提供的“newrbe”调用函数,该函数直接确定了神经元个数,不需人为试算。本文算例选用“newrbe”函数计算结果图4进行对比分析。
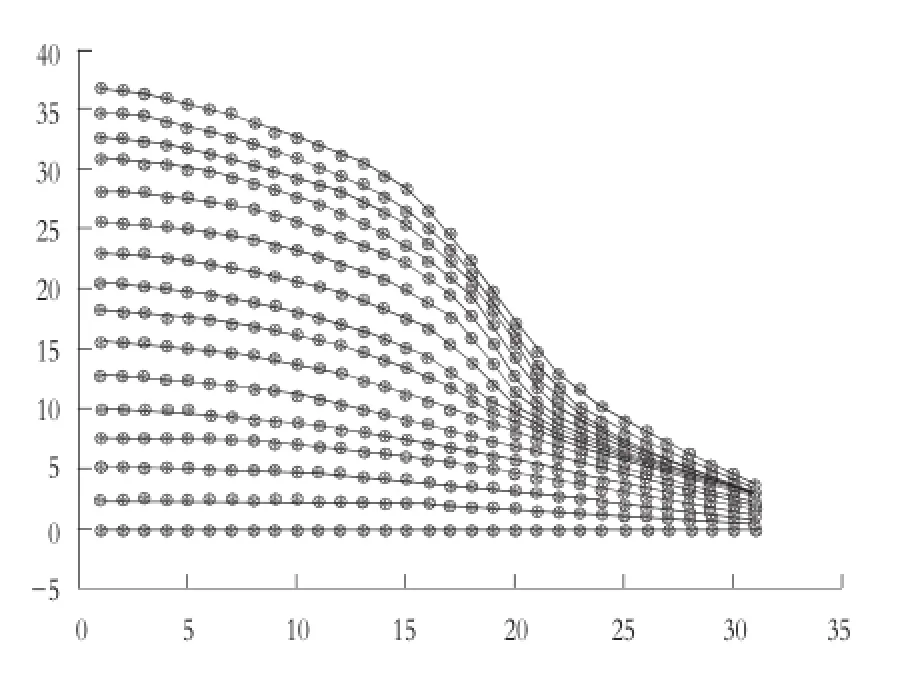
图4 流量特性曲线实际值与预测值图
3 结论
1)BP网络和RBF网络训练生成的网络均可以用以预测水轮机流量特性,其中BP网络(隐含层神经元个数取大于15个)误差为±4L/s流量之间,相对于最大值400L/s)的相对偏差范围在1%以内,其精度用在普通数据处理上,已经足够。因为仅仅靠经验拟合时,其偏差范围亦在该差值左右。同时用RBF隐含层神经元个数固定的模型计算结果其绝对误差在±1.5×10-12L/s之间,其精度非常高,完全满足普通数据处理的需要。
2)RBF网络预测误差为±1.5×10-12L/s之间,远远小于BP网络预测误差±4L/s的结果。这种对比本身存在一些问题,因为BP网络的隐含层神经元个数不固定,需要通过人工调整来实现最佳神经元个数的拟合,这本身需要相当丰富的经验。同时由于每次改变隐含层神经元个数均需要重新训练,训练的初始值又是随机给定的,因此整个训练过程需要花去一定的时间,从而使得在1~100个隐含层神经元个数的寻早过程就较长。而RBF固定隐含层神经元个数的调用方法“newrbe”却能一下子将神经网络进行训练求解,从而预测出所需要的值,其预测精度非常高,训练时间又很短,因此就时间长短及寻找网络方便程度的情形下,认为RBF网络的模拟精度要高于BP网络。
3)正是由于BP网络通过寻找最优隐含层神经元个数(15个)后与RBF网络分别达到的预测误差级别相差太大,因此想找寻BP网络是否可以通过提高隐含层神经元个数来提高网络的模拟精度。研究表明,两层网络在其隐含层中使用S形传输函数,在输出层中使用线性传输函数,就几乎可以以任意精度逼近任何感兴趣的函数,只要隐含层中有足够的单元可用[4]。该观点表明,在单隐含层的BP网络中,只要隐含层神经元个数足够,网络的预测精度应该是会有相应提高的。但是当隐含层神经元个数从超过最佳个数15到一直增加到100个的过程中,其精度不但没有提高反而程一定的波动状态,甚至接近100时,其预测误差在增加。当隐含层神经元超过100~300过程中,预测误差反而越来越大。
[1]谭剑波,把多铎,高立明,等.基于BP神经网络的水轮机综合特性建模仿真[J].中国农村水利水电,2010(03):140—142,145.
[2]黄贤荣,刘德有.利用径向基函数神经网络处理水轮机综合特性曲线[J].水力发电学报,2007,26(01):114—118.
[3]周继成.人工神经网络[M].北京:科学出版社,1993.
[4]MartinT.Hagan,HowardB.Demuth,MarkH.Beale著,戴葵等译.神经网络设计[M].北京:机械工业出版社,2005.
TV734.1
A
1002-0624(2015)12-0059-04
2015-08-20

