多抽样率原理在舰船振动信号分析中的应用与研究

沙长源，蔡萍

（上海交通大学仪器科学与技术系，上海200240）

多抽样率原理在舰船振动信号分析中的应用与研究

沙长源，蔡萍

（上海交通大学仪器科学与技术系，上海200240）

船舶航行过程中产生的振动会影响船上人员的舒适性、降低船体结构耐久性并影响舰船的隐身性能。船体振动评估对于船舶的防振隔振设计、确定振动量级并判断是否满足衡准要求具有重要意义。随着技术的进步和使用要求的提高，对船体振动评价的客观性和全面性也越来越高。倍频程分析是振动分析中常用的频率分析方法，早期的方法是带通滤波器法，需要采用大量的滤波器以提高频率分辨率，导致计算量大运算时间长。为此，提出了基于多抽样率原理的倍频程频域方法。论文对该频域方法进行了详细介绍，对方法的谱分辨率、计算量和存储空间进行了分析对比，基于FPGA搭建了船舶振动采集分析系统，在FPGA中对算法进行了实现，最后对实测船舶振动信号应用多抽样率倍原理进行了倍频程分析。

振动分析；倍频程；频域分析；多抽样率原理；FPGA

船舶振动会影响船上人员的舒适性、降低船体结构耐久性并影响舰船的隐身性能［1］。船舶结构多为整体结构，质量大，固有频率低，因此船舶振动分析要求在低频范围内具有较高的频率分辨率。随着船舶的高速化发展，发动机和船载设备的功率逐渐提高，船舶振动频率也向高频逐渐发展。因此对船舶振动的倍频程分析不仅要求要具有一定的频率宽度，同时在低频范围内还需要具有良好的分析精度。

舰船航行时经常处于不同工况，每种工况下船舶不同的运行状况会引起不同的船舶振动，为了客观全面的分析不同工况下的船舶振动，需要对振动信号进行实时的测量和分析。舰船在执行远洋航行任务时测控系统长时间为无人值守状态，要求具有较高的可靠性和较大的存储空间来存放采样数据和分析结果。

倍频程分析是振动分析中常用的分析方法。传统的倍频程分析是由时域带通滤波器组实现的，信号通过不同中心频率的滤波器组后进行时域积分得到每个频带的功率。频域内倍频程分析是对采样信号加窗后进行FFT变换，将谱线在每个倍频程频带内进行加权处理即可得到倍频程谱线。为提高时域滤波法的频谱分析精度，需要大量的滤波器，并要求滤波器的阶数足够高，导致计算量大，运算时间长。频域方法的分析精度由信号帧长度决定，从低频到高频分辨率相同。为提高低频分辨率，只能增加FFT点数，但会造成计算量严重增加。本文采用了基于多抽样率原理的频域倍频程分析方法，使倍频程分析在高频和低频端都具有较高频率分辨率。

FPGA具有高速、高集成、高可靠性、低功耗等特点。由于FPGA采用硬件语言编写，使它具优良的高速性能，便于进行实时分析。结合多抽样率原理可以有效兼顾高频端和低频端的频率分辨率与存储容量需求间的矛盾，提高实时监控系统的性能。

1　基于多抽样率原理的高分辨率倍频程分析

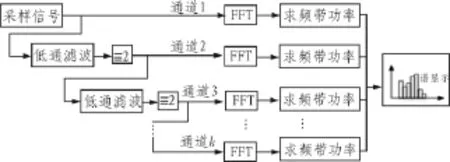
图1　基于多抽样率原理的倍频程分析算法框图Fig.1Octave analysis based on multirate principle

振动信号经过AD采样之后逐级经过抗混叠滤波器并且进行2倍抽样，将原信号划分为若干采样频率不同的频段，再对每频段做点数相同的FFT变换后求频带功率即可显示为倍频程谱。

1.1算法原理介绍

多抽样率频域算法的实质是通过低通滤波和2倍抽取，逐级降低信号的采样频率，从而对原采样信号进行频率分段，并对每频段做相同点数FFT变换，由于各频段的采样频率逐级降低，频率分辨率得以提高。设通道1每帧数据点数为N，经过滤波抽取后作为通道2的采样数据，点数为N/2，通道1下一帧数据经滤波抽取后合并到通道2，再对通道2的N点数据进行滤波抽取作为通道3的采样数据，以此类推。数据滤波抽取的示意图如下，图中每个方块代表一个帧（N点），通道个数k由分析的频率范围确定。

图2　多抽样率算法数据抽取示意图Fig.2Data synthesis of multirate principle

从图2可以看出，通道1的2k-1个信号帧可合成一个通道k的信号帧，即通道k的信号帧每Tk=T*2k-1时间刷新一次。因此高频部分的频带刷新速率快，低频部分的频带刷新速率慢，符合振动信号频率特性。N点FFT变换的频率分辨率为：

其中fs为信号的采样频率，Ts为采样周期，T为信号帧的长度。初始的采样信号经过各级逐级抽取，为后续的FFT变换提供了不同采样频率的信号，低频信号经过的抽取级数多，采样频率相应降低。由于数据长度N保持不变，因此低频段的分析精度得以提高。采用多抽样率算法解决了直接频域分析方法的分辨率低、分辨率单一的问题。

1.2抽取过程分析

2倍抽取就是把原始的采样序列每隔2个点取一个点，形成新的采样序列［2-3］。设输入信号为x（n），输出信号为yD（n），则2抽取后输入输出的关系为：

据悉，《大漠驼铃》由知名编剧阮剑文创作，颜丙燕主演，以哈萨克斯坦为故事主要发生地，以西安外国语大学“最美教师”邓滢为人物原型，讲述女教师石榴花面临家人的不解、身体病痛的折磨、异域文化的冲击以及办学条件的艰苦，克服种种困难，在哈萨克斯坦欧亚大学孔子学院推广汉语的故事。影片将通过塑造石榴花“一带一路”文化大使的形象，传播中国声音，展示中国形象，架起中哈两国文化交流的桥梁。

输入信号x（n）与2倍抽取后的输出信号yD（n）在频域的关系如下：

对原信号进行2抽取实际上将信号的采样频率降低了2倍。从式（3）可以看出相邻的样本频谱在ω对应的频率轴上相差π，为了避免抽取后的混叠，需要采取抗混叠滤波把信号x（n）的带宽必须限制在［-π/2，π/2］。图3为一个抽取滤波过程的示意图。

图3　带有抗混叠滤波器的抽取器框图Fig.3Decimator diagram with anti-aliasing filter

图3中h（n）为抗混叠滤波器，其频率响应近似为

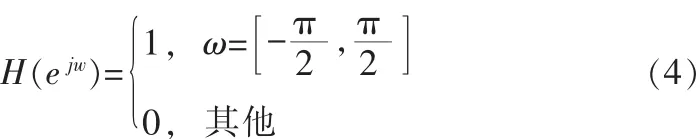
这样信号的高频部分被滤除，保留了有用的低频部分，防止了抽取后的频率混叠。

1.3滤波器设计

滤波器在多抽样系统中起到限制信号频带的重要作用，半带滤波器是一种重要的多抽样率信号滤波器，常用于对信号做的整数倍的抽取或者插值［4］。图4为Matlab Filter Design工具箱设计的23阶半带滤波器幅频曲线，阻带衰减为40 dB，通带归一化频率为0.4，设计方法为等波纹法。40d B的阻带衰减可以满足滤波器的基本性能需求。半带滤波器有接近一半的滤波器系数均为0，不仅存储滤波器系数的存储器可以减少一半，并且使得滤波运算的乘法次数减少了近3/ 4，加法次数减少了近一半，更有利于硬件和高速实时数字信息处理的实现［5］。

图4　23阶半带滤波器幅频特性曲线Fig.423-order half-band filter amplitude-frequency characteristic

由于半带滤波器通带的边频ωp和阻带的边频ωs相对于π/2对称，在（0.5，ωs）内的频率分量在2倍抽取之后仅仅会折叠进（ωp，0.5）。因此在半带滤波器的通带（0，ωp）内，2倍抽取之后不存在频率混叠。

根据半带滤波器的通带宽度和抽取倍数即可对采样信号在［0～fs/2］的频率范围内划分为若干个频带。设共划分为k个通道，通道1不经过低通滤波和采样，频率范围为［0，fs/2］，通道2经过低通滤波抽取后采样频率为fs/2，有效频率范围为［0，ωpfs/4］，以此类推，通道k的采样频率为fs/2k-1，有效频率范围为［0，ωpfs/2k］。这样即可将频带［0，fs/2］划分为：

划分好频段之后即可对每个频段进行相同点数的FFT变换。一般来讲一个频带至少需要5-10条谱线才能正确的合成出一个倍频程频带［6］。若采样频率fs=10 kHz，多抽样率分析方法在低频范围内达到0.1 Hz的频率分辨率需要N至少为391点，规整到点数2k为512。而传统的频域倍频程方法要达到同样精度需要至少N=131 072，这显然是难以实现的。

在对信号进行FFT分析时的截断会引起频谱泄漏，需要对信号进行加窗处理。在振动信号处理中常用的一种窗是余弦坡度窗，即有矩形窗频率主瓣窄、谱值衰减小，又有汉宁窗旁瓣小的特点，有较好的抑制谱泄漏效果［7］。

多抽样率倍频程频域算法将整个频带划分为不同频率分辨率的频段，倍频程谱线可以由不同频段的功率谱密度函数按频率分辨率加权得到，如式（6）所示：

式（6）中PSD（k）为功率谱密度函数的第k条谱线，Δfk为该谱线所在频段的频率分辨率。

2　计算量和存储容量分析对比

2.1计算量分析

下面对直接FFT法和多抽样率算法达到相同低频分辨率所需的计算量作分析比较。由（1）式可知，直接法需要做N=2k-1N0点FFT来达到多抽样率算法第k个通道的频率分辨率。N点FFT计算需要复数乘法Nlog2N/2次。直接法FFT需要的复数乘法次数为：

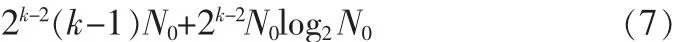
多抽样率算法每帧采集N0个数据，通道1共2k-2帧，通道2共2k-2帧…通道k共1帧，每帧数据均做N0点FFT，各通道FFT复数乘法次数之和为：

式（8）也可写作

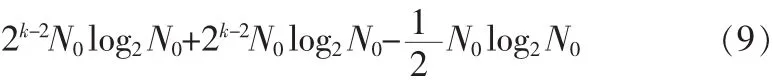
式（9）的最后一项较前两项相差很大，第二项和式（7）第二项相同，故要比较计算量只要比较两式的第一项，即比较k-1和log2N0。若多抽样率算法有9通道，进行256点FFT时两者运算量基本一致。

除通道1的信号每帧都要处理，通道2～k的信号帧在一帧采样时间内需要处理的平均次数为次。可以通过合理安排来避免FPGA需要同时处理2个以上通道数据的情况，减少了FPGA运算量，因此多抽样率算法的运算量不随抽取次数的增加而增加。

2.2存储容量分析

直接法达到相同分析精度需要采样2k-1N0点后做FFT变换，直接法需要占用2k-1个N0大小的存储空间，随着分析精度的提高存储容量需求大量增加。多抽样率频域分析算法每个通道只需要一个N0大小的存储空间，每个通道的采样数据存储至指定长度后即可进行谱分析，然后经过滤波抽取作为下一个通道的采样数据存储到下一个通道的存储空间，k个通道只需要占用k个存储空间。多抽样率算法把数据的存储容量从2k-1减少到k，在实现高分辨率的同时极大的减少了需求的存储容量。

进行振动信号分析时采集到的数据要缓存在FPGA的片内RAM上，采集完毕后进行FFT处理，由于FPGA的RAM大小有限因此限制了直接FFT法的数据长度，应用多抽样率方法可以极大的减少FPGA需求的RAM大小。

3　舰船振动数据采集系统设计

舰船振动数据采集装置要求同步采集船舶上各观测点的横向振动、垂向振动和纵向振动信号，采样频率不低于10KHz。装置选用FPGA为主控器进行数据采集和处理，使用Cyclone III系列的EP3C16芯片构建最小系统，并且在最小系统的基础上进行外扩。系统包括抗混叠滤波电路、高精度ADC、Flash数据存储芯片、USB数据通信、日历芯片以及无线通信模块。图5为振动数据采集装置系统框图。

图5　振动采集装置系统框图Fig.5Vibration acquisition system

加速度传感器选用的是美国PCB公司的356A32型三轴加速度传感器，可同时敏感三向振动信号，灵敏度100 mV/g，测量范围为±50 g，频率响应范围为1到4 000 Hz，传感器响应时间小于2秒。ADC模块选择ADI公司的AD7656，芯片内部有6个16位的逐次逼近型ADC，吞吐速率可以达到250kSPS，可实现三路振动信号同时采集。USB传输芯片选用的是Cypress的公司CY7C68013A，工作在Slave FIFO模式下。Flash存储芯片选用现代8Gb NAND芯片H27UCG8T2M，时钟芯片选择PHILIPS公司日历芯片PCF8563，无线模块嵌入式串口转WIFI模块USR-WIFI232-A，该模块可以实现TTL与WIFI之间的双向透明传输。

FPGA内部的IP（Intellectual Property）内核可以将一些通用的功能如FFT变换、FIR滤波等设计为可修改参数的模块。在FPGA中采用级联积分梳状滤波器（CIC滤波器）［8］和特殊FIR滤波器（半带滤波器）级联的形式进行多抽样率的抽取滤波，并使用IP核实现FFT运算。

4　舰船振动实测数据分析

对船舶振动采集系统在某型号舰船上采集得到的振动数据进行分析。图6和图7为舰船尾甲板处Z方向振动数据的1/3倍频程谱线和基于多抽样率原理的1/12倍频程谱线。

图6　Z方向振动信号1/3倍频程谱线Fig.61/3 octave spectrum of Z direction vibration signal

图7　Z方向振动信号多抽样率原理1/12倍频程谱线Fig.71/12 multi rate octave spectrum of Z direction vibration signal

尾甲板的振动响应主要集中在低频范围，尤其在10 Hz到20 Hz之间，倍频程谱线明显出现了一个或多个波峰。这与螺旋桨的叶频激振力频率是比较符合的，该工况下螺旋桨转速为300转/min，螺旋桨为3叶，对应叶频激振力频率为15 Hz左右。从图6和图7中可以看出，在对振动信号进行1/ 3倍频程分析时，低频内多条单独的谱线被合成在了一个1/3倍频程频带之内，而采用1/12倍频程之后可以明显的看出单个谱线其实是由不同的频率分量组成的，采用多抽样率倍频程分析可以有助于获得更加清晰的分析结果。

5　结论

多抽样率倍频程算法克服了直接法频率分辨率固定的缺点，在低频端和高频端都获得了良好的频率分辨率。应用多抽样率原理进行实时倍频程分析可减少振动监控系统的运算负担、降低对采样数据存储空间的需求。实测振动数据分析结果显示多抽样率倍频程分析结果更清晰，为准确估计船舶振动的共振频率和船舶防震隔震设计提供了依据。

［1］赵耕贤.船舶与海洋结构物设计中的关键技术——船舶振动［J］.船舶，2001（52）：35-40. ZHAO Geng-xian.Ship vibration——one of the key design factors for ship and offshore structure［J］.SHIP&BOAT，2001（52）：35-40.

［2］胡广书.数字信号处理——理论、算法与实现［M］.北京：清华大学出版社，2003.

［3］陶然.多抽样率信号处理理论及其应用［M］.北京：清华大学出版社，2008.

［4］冯通，陈华.基于多采样率的频域倍频程研究［J］.声学技术，2011，30（3）：289-293. FENG Tong，CHEN Hua.Research on multi-rate spectrum in octave analysis［J］.Technical Acoustics，2011，30（3）：289-293.

［5］王静，杨梅，刘涛.半带抽取有限冲激响应滤波器的应用设计及仿真［J］.大连海事大学学报，2004，30（2）：57-60. WANG Jing，YANG Mei，LIU Tao.Application design and simulation of HB decimation FIR filters［J］.Journal of Dalian Maritime University，2004，30（2）：57-60.

［6］JAMES W W.A multirate bank of digital bandpass filters for acoustic applications［J］.Hewlett-Packard Journal，1993：73-81.

［7］王济，胡晓.MATLAB在振动信号处理中的应用［M］.北京：水利水电出版社，2006.

［8］王建勋，刘会金.基于AR谱估计和频谱分析的间谐波检测方法［J］.陕西电力，2014（7）：23-30. WANG Jian-xun，LIU Hui-jin.An interharmonic detection algorithm based on AR spectral estimation and spectrum analysis［J］.Shaanxi Electric Power，2014（7）：23-30.

Multi-rate spectrum octave analysis of ship vibration

SHA Chang-yuan，CAI Ping
（Shanghai JiaoTong University Dept of Instrument Science and Engineering，Shanghai 200240，China）

Vibration is one of the main factors affecting the habitability of ships，degrading the durability of the ships'structure and stealth performance as well.Estimating the vibration of ships is important for both vibration isolated designing and evaluating whether the magnitude of vibration meets the criterion.The requirements of objectivity and comprehensiveness for ship vibration evaluation become more and more demanding.Octave frequency spectrum analysis method is a commonly used in vibration analysis.The bandpass filter bank method is commonly used to implement octave analysis，but that incurs heavy computation when large amounts of filtering calculation are needed in order to improve the frequency resolution.Therefore，a multi-rate octave analysis method is proposed and introduced in detail.Resolution，computational complexity and memory space of the two methods are compared.The algorithm is implemented in FPGA based ship vibration data acquisition system，and the collected vibration data is analyzed via multi-rate spectrum octave method.

vibration analysis；octave；frequency domain analysis；multi-rate；FPGA

TN911

A

1674-6236（2015）20-0110-04

2015-01-14稿件编号：201501113

沙长源（1990—），男，上海人，硕士研究生。研究方向：动态检测、测试计量技术。