自旋电子学材料：Fe4N薄膜及其异质结构

2015-10-31 02:32:30米文博

物理学进展 2015年4期

关键词：磁滞回线外延偏置

米文博*

天津大学物理系天津市低维功能材料物理与制备技术重点实验室天津300072

自旋电子学材料：Fe4N薄膜及其异质结构

米文博*

天津大学物理系天津市低维功能材料物理与制备技术重点实验室天津300072

本文综述了在自旋电子学器件上具有潜在应用前景的钙钛矿结构的Fe4N薄膜及其异质结构的研究成果和最新进展情况。文章从引言开始，介绍了钙钛矿结构Fe4N的晶体结构和基本性质；之后对多晶Fe4N薄膜、外延Fe4N薄膜、Fe4N/CoN双层膜、Fe4N/Alq3/Co自旋阀、以Fe4N为电极的隧道结的形貌、晶体结构、磁性、交换偏置、自旋相关的电输运特性和磁电阻效应进行了介绍；最后对Fe4N材料的相关研究结果进行了简单的总结和展望。

自旋电子学；Fe4N薄膜；自旋阀；隧道结；表面形貌；晶体结构；磁性质；电输运特性；磁电阻效应

I.引言

随着人类社会的不断发展，如何能更高效的存储信息受到人们的普遍关注。传统的微电子学器件利用电子的电荷属性来处理信息，但是存在断电易失等缺点。电子除了具有电荷属性之外，还有一个内禀属性-自旋，而利用自旋来存储信息将不易丢失。1988年，法国科学家Fert与德国科学家Grnberg分别在Fe/Cr多层膜中发现巨磁电阻（GMR）效应［1，2］，它的发现为信息存储中自旋的利用提供了可能性。GMR效应是一种量子效应，其产生机理是自旋相关的散射。这一发现很快就被应用到磁盘驱动的读出磁头与磁性传感器当中。因为在自旋电子学方面的杰出贡献，Fert和Grnberg共同获得了2007年的诺贝尔物理学奖。

自旋电子学通过控制复合（异质）结构中电子自旋的产生、注入、输运与检测，并利用传统的半导体工艺的光刻和大规模集成技术，制备出稳定的、抗辐射、非易失的、低功耗、高集成、高速度的自旋电子学器件，形成可以替代微电子学器件的新一代信息处理技术。自旋电子学的物理学基础为磁电阻效应（GMR）和隧道磁电阻效应（TMR）分别源自电子传输过程中的自旋相关的散射和自旋相关的隧道效应。理论研究表明，TMR数值正比于铁磁性电极材料的自旋极化率［3，4］，而且在人们提出的各种原型自旋电子学器件中，如自旋发光二极管、自旋p-n结二极管、自旋场效应管等，都需要自旋极化率尽可能高的电子（自旋）注入源和尽可能高的自旋注入效率。所以，寻找具有高自旋极化率的铁磁性材料并将其与半导体材料复合形成器件是目前自旋电子学领域最为活跃的研究方向之一。

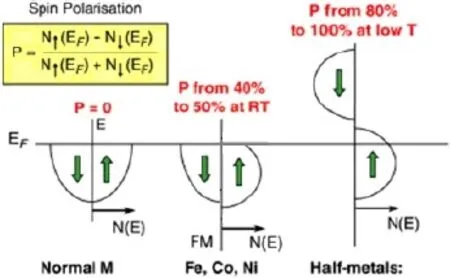
图1.正常金属、铁磁性金属和半金属的能态密度示意图［5］

将铁磁性材料应用于自旋电子学器件，必须实现自旋从高自旋极化的铁磁性材料向半导体材料的高效自旋注入且与现有的半导体工艺相兼容。实现自旋注入的方法主要有两种方式［6］：（1）通过在直接带隙半导体中吸收圆偏振光；（2）通过铁磁性电极向半导体中进行自旋注入。寻找高自旋极化率的铁磁性电极材料是解决自旋注入问题的重要前提条件。第一性原理计算表明［7-9］，Fe3O4、La1-xAxMnO3（LAMO，A为碱土元素Ca、Sr和Ba等）、CrO2、NiMnSb（Heusler合金）等材料的能带结构介于金属和绝缘体之间，被称为半金属材料（Half-metal）。对于一个自旋方向，半金属材料的能带结构具有金属特性，在费米面附近具有一定的态密度；而对另一种自旋方向，其能带结构具有绝缘体特性，在费米面附近态密度为零或电子是局域化的，如图1。因此，从理论上讲，半金属材料应具有100%的自旋极化率。由于需要与不同的材料进行复合，需要不同电阻率的高自旋极化的磁性材料。因此，寻找具有高自旋极化率的新型铁磁性电极材料是进一步发展自旋电子学器件的关键因素和研究热点。Kokado等从理论上分析了钙钛矿结构的块体Fe4N的自旋极化率，结果显示Fe4N具有很高的自旋极化率（如图2），从而成为自旋电子学器件中的新型铁磁性电极材料［10］。本文将对Fe4N薄膜及其异质结构的相关研究结果进行简单的总结与综述。

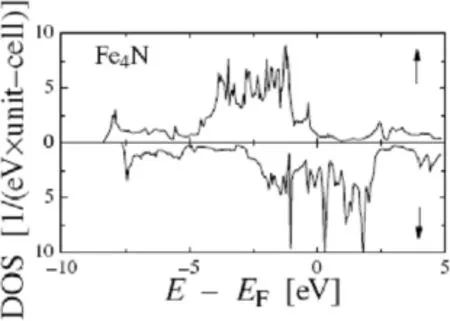
图2.Fe4N的能态密度示意图［10］

II.Fe4N的晶体结构和基本性质

氮化铁材料具有优异的铁磁性、良好的耐磨损、抗腐蚀、抗氧化能力而被广泛应用到高密度磁性存储记录和读出磁头中。氮化铁由于氮含量的不同，存在复杂的相结构。随着氮含量的增加，会有α-Fe（N）、α′-Fe8N、α′′-Fe16N2、γ′-Fe4N、ε-Fe3N、ξ-Fe2N、γ′′-FeN、γ′′′-FeN等相［11］，见图3。其中在铁磁氮化物中，Fe4N除了具有很好的机械性能之外，还具有良好的金属导电性、化学稳定性及热稳定性、高居里温度、高饱和磁化强度、高自旋极化率、晶体结构简单等，成为磁性材料和自旋电子学等领域的研究热点之一。但是从相图中可以看出，Fe4N的存在窗口很窄，因此纯相Fe4N薄膜的制备成为难点。

Fe4N具有钙钛矿结构，属立方晶系，空间群为pmm，晶格常数为3.795˚A。晶体结构中含有两种不同的Fe原子位，FeI占据顶角位置，FeII占据面心位置，N原子占据体心位置，相当于在面心立方结构γ-Fe的体心位置插入一个N原子。Fe4N的晶体结构如图4所示。Fe4N具有很好的热稳定性，居里温度为767 K，室温饱和磁化强度为1440 emu/cm3［13］，各向异性常数为2.9×104J/m3［14］。FeI与FeII比为1：3，二者的磁矩分别为2.98和2.01µB［15］。FeI的磁矩大于FeII是由于FeII与体心位置的N原子距离要比FeI近，致使它与N原子之间形成更多的结合键［16］。理论计算表明Fe4N的自旋极化率接近-100%，这一值是面心立方的γ-Fe的2.5倍，自旋极化率的增大是由于引入N原子增强了3d能带的输运贡献，而负的自旋极化率则是来源于占主导的3d自旋向下的能带。

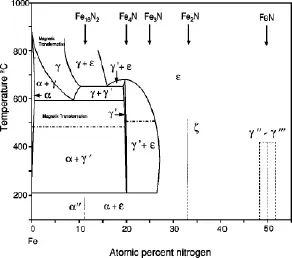
图3.Fe-N二元相图

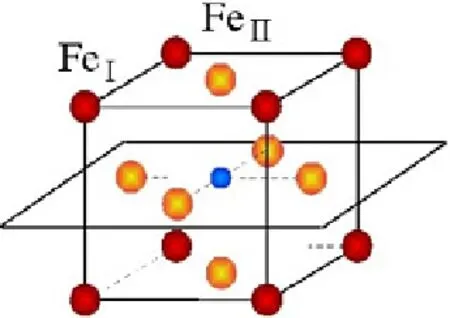
图4.Fe4N的晶体结构示意图［12］

Fe4N含氮量为20%，在700◦C以下能稳定存在。Fe4N薄膜通常是用Fe和N2反应来制备。常见的Fe4N薄膜的制备方法有：分子束外延法［17，18］，化学气相沉积法［12］，直流磁控溅射法［19］等。除了直接制备Fe4N薄膜之外，还可以通过氮化Fe薄膜［20］或是间接的热处理方法［21］来制备出单相的Fe4N。由于Fe-N系统复杂的相结构，制备Fe4N对基底温度与氮气流量有很高的要求［22］。Fe4N在低温下，氮气比例范围很窄，氮气过量会出现ε-Fe3N，氮气不足会出现α-Fe。温度过高，Fe4N会分解。因此可以通过热退火或者氮化处理来得到单相Fe4N薄膜，也可以严格控制基底温度和氮气流量来直接制备Fe4N薄膜。Mi等人已经在Si、MgO（100）、LaAlO3（100）、SrTiO3（100）等基底上利用对向靶溅射制备了不同取向的多晶和外延Fe4N薄膜［23］。

III.多晶Fe4N薄膜的结构与物性

本节我们将重点介绍多晶Fe4N薄膜的表面形貌、晶体结构、磁性、电输运特性和磁电阻效应［24，25］。

A.多晶Fe4N薄膜的结构

图5给出了450◦C下Si（100）基底上的不同厚度的Fe4N薄膜的扫描电镜（SEM）图像［24，25］。从图中可以看出，薄膜表面的颗粒尺寸随着薄膜厚度的增加而逐渐增大，颗粒的形状也从不规则的圆形逐渐趋向于方形。对于同一厚度的薄膜，上层颗粒的尺寸大于下层的颗粒尺寸；并且随着薄膜厚度的增加，上层较大尺寸的颗粒数量增多。上述表面形貌随着薄膜厚度的变化可能是由于在薄膜比较薄时，制备时样品在450◦C的停留时间较短，颗粒趋于小的均匀的圆形形状存在。随着薄膜厚度的增加，制备时沉积时间长，样品在450◦C的停留时间变长，有更多的能量使得小颗粒汇聚成大的颗粒。按照这样的趋势，如果薄膜足够厚，薄膜表面的颗粒尺寸就应该大且均匀［24，25］。从断面SEM图像上可以看出，样品为柱状生长，如所6所示。

图7给出了450◦C下Si（100）基底上的不同厚度的Fe4N薄膜的X射线θ-2θ扫描图。从图中可以看出，不同厚度的氮化铁薄膜都只有Si基底和Fe4N的衍射峰出现，说明在450◦C时在Si基底上制备出了单相的多晶Fe4N薄膜。此外，随着薄膜厚度的增加，可以发现来自Si基底的衍射峰也是有区别的。在2θ=69.22◦峰位处的Si（400）衍射峰，随着薄膜厚度的增加逐渐向高角度偏移，并且衍射峰的半高宽的宽度逐渐增大，这很可能是因为随着薄膜厚度的增加，出现了Fe4N（220）衍射峰引起的［24，25］。Fe4N（220）衍射峰对应的衍射角是70.17◦，与Si（400）衍射峰比较接近。厚度为163 nm的薄膜在这一峰位处可以较明显地看出Fe4N（220）衍射峰。随着薄膜厚度的逐渐增加，Fe4N（111）和（200）衍射峰的强度逐渐增强，并且从58 nm开始，随着薄膜厚度的增加，逐渐出现了Fe4N（311）和（222）衍射峰。然而，当薄膜厚度为10 nm时，除了Si基底的衍射峰外，只能观察到弱的Fe4N（200）衍射峰，这是由于薄膜厚度相对太薄，因此参与衍射的晶面数目较少。用Bragg公式和Scherrer公式，计算了在450◦C下Si（100）基底上制备的厚度为163 nm的Fe4N薄膜的晶格常数和晶粒尺寸。通过计算得到Fe4N薄膜的晶格常数约为3.798˚A，与通过理论计算得到的理论值3.795˚A很接近。得到Fe4N薄膜的晶粒尺寸为∼32 nm［24，25］。

图5.多晶Fe4N薄膜的SEM图像，膜厚为（a）26、（b）58、（c）91和（d）163 nm［24，25］

图6.多晶Fe4N薄膜的断面SEM图像［25］

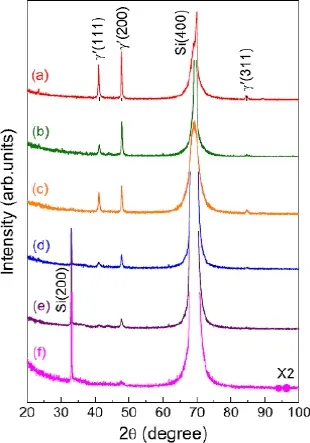
图7.多晶Fe4N薄膜的X射线θ-2θ扫描图，膜厚为（a）163、（b）91、（c）84、（d）58、（e）26和（f）10 nm［24，25］

图8给出了NaCl基底上制备的10和91 nm的Fe4N薄膜的TEM明场像和相应的选区电子衍射图

［24，25］。从图8（a）可以看出，在10 nm的Fe4N薄膜中晶粒呈现出无规则的形状，晶粒尺寸约为20∼40 nm。晶粒之间白色区域表明薄膜中存在着无序原子或面间距较小的晶格。图8（b）为10 nm的Fe4N薄膜对应的选区电子衍射图，电子衍射环均来自于Fe4N（111）、（200）和（220）及相对弱的（100）和（110），并没有其它氮化铁相的衍射环出现，进一步说明薄膜为单相的Fe4N。从图8（c）中可以看出，晶粒尺寸约为80∼100 nm，比10 nm厚的薄膜中的晶粒尺寸大。晶粒边界处仍存在着无序原子或面间距较小的晶格。从图8（d）可以看出，选区电子衍射环同样来自于Fe4N（111）、（200）和（220）及相对较弱的（100）和（110）。由此可见，在450◦C下制备出的不同厚度的薄膜均为单相的多晶Fe4N薄膜［24，25］。

B.多晶Fe4N薄膜的磁性

采用超导量子干涉仪在不同的温度下测量了Si（100）基底上不同厚度的多晶Fe4N薄膜的磁滞回线。测量时外加磁场平行于薄膜表面，最大外加磁场为50 kOe。图9给出了不同温度下的5 nm的多晶Fe4N薄膜的磁滞回线。插图给出了薄膜的饱和磁化强度Ms和矫顽力Hc随着温度的变化关系曲线。从图中可以看出，Fe4N薄膜呈现出软磁性。Fe4N薄膜的Ms随着温度的升高而逐渐减小，当温度为5 K时，Ms为1128 emu/cm3，随着温度升高到300 K，Ms减小到最小值830 emu/cm3。Fe4N薄膜的Hc随着温度的升高而减小，当温度高于100 K时，Hc随着温度的升高基本保持为24 Oe不变。当温度为5 K时，Hc有最大值404 Oe，随着温度升高到50 K，Hc减小为125 Oe［24，25］。

图8.多晶Fe4N薄膜的TEM图像和选区电子衍射图，膜厚为（a）（b）10、（c）（d）91 nm［24，25］

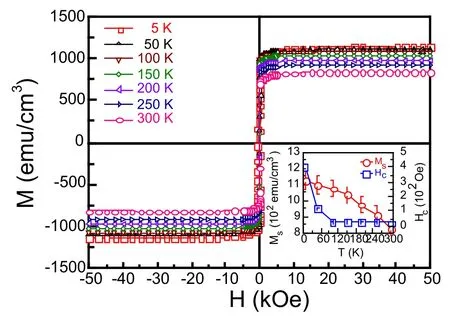
图9.不同温度下，5 nm的多晶Fe4N薄膜的面内磁滞回线，插图为Ms和Hc随着温度的变化关系曲线［24，25］

图10给出了厚度分别为5、91、163 nm的多晶Fe4N薄膜的Ms随着温度的变化曲线［24，25］。对于单位体积的铁磁性样品而言，原子间存在着交换作用，交换积分大于零。当温度等于零时，铁磁体处于基态，各原子的电子自旋平行取向，表现出最大的磁化强度（绝对饱和磁化）。当温度升高时，由于热激发效应使得一部分原子的电子自旋反向，这种反向的自旋不是固定在某个或某几个原子上而是以波的形式在整个铁磁晶体中传播，这就是由布洛赫通过理论推导提出的自旋波的概念［26］。基于布洛赫自旋波的理论，可以得到铁磁性样品的饱和磁化强度与温度T之间满足一定的关系。布洛赫提出的有关饱和磁化强度与温度T满足下面的关系式［26］

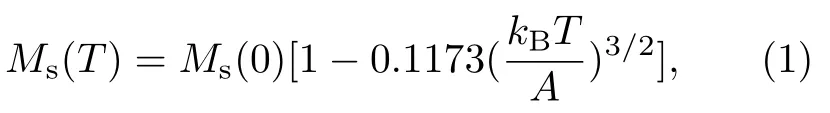
图10.不同厚度的多晶Fe4N薄膜的Ms随着温度的变化关系曲线［24，25］

其中，kB为玻尔兹曼常数，A为交换积分常数。上式称为布洛赫的T3/2定律。由于布洛赫的自旋波理论忽略了自旋波之间的相互作用，所以这一定律在较低的温度范围是与实验结果符合的。随后，戴森考虑了自旋波之间的相互散射问题，修正了布洛赫的T3/2定律。戴森修正后的关系式为［26］

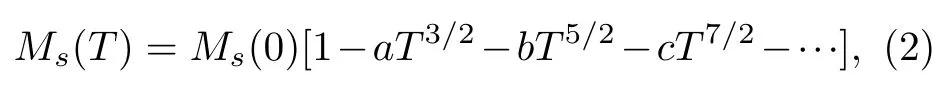
其中a、b和c是相关的系数。式（2）适用于较高的温度。我们采用式（1）和（2）对厚度为5、91、163 nm的多晶Fe4N薄膜的Ms随着温度的变化进行了拟合。采用布洛赫的T3/2定律不能进行很好的拟合，采用由戴森修正后的式（2）可以很好的对实验数据进行拟合，如图10中的实线所示［24，25］，图中三角形、圆形和正方形的点为实验数据点。可见在5∼350 K的温度范围内，存在着自旋波相互作用。对于厚度为5 nm的多晶Fe4N薄膜的拟合所得数据如下：Ms（0）=1128 eum/cm3、a=3.579×10-4K-3/2、b=9.922×10-7K-5/2和c=2.319×10-19K-7/2。对于厚度为91 nm的多晶Fe4N薄膜的拟合所得数据如下：Ms（0）=1370 eum/cm3、a= 1.399×10-8K-3/2、b=0和c=4.879×10-19K-7/2。对于厚度为163 nm的多晶Fe4N薄膜的拟合所得数据如下：Ms（0）=1201 eum/cm3、a=1.537×10-8K-3/2、b=0和c=3.055×10-19K-7/2。同时根据a=0.1173（kB/A）3/2我们可以求出交换积分常数A。厚度为5 nm的多晶Fe4N薄膜的交换积分常数A=8.670×10-22。对于厚度为91 nm的多晶Fe4N薄膜，交换积分常数A= 5.699×10-19。对于163 nm的多晶Fe4N薄膜，交换积分常数A=5.355×10-19［24，25］。

C.多晶Fe4N薄膜的电输运特性

图11给出了玻璃基底上不同厚度的多晶Fe4N薄膜的ρ（T）/ρ（305 K）随着温度的变化曲线［24，25］。从图中可以得出，样品的电阻率随着温度的降低而减小，表现为金属导电特性。插图给出了室温下多晶Fe4N薄膜的电阻率随着薄膜厚度的变化曲线。随着Fe4N薄膜的厚度从5 nm增加到163 nm，薄膜的电阻率逐渐减小，这主要是由于随着薄膜厚度的增加，薄膜中的晶粒尺寸逐渐增大，引起薄膜中晶界减少，导致对传导电子的散射减小造成的。同时薄的薄膜表面对电子的散射也会使得薄的薄膜的电阻率比厚的薄膜的电阻率大［24，25］。

众所周知，导体中的ρ起源于不同的散射机制，总的ρ可以表示为［24，25］

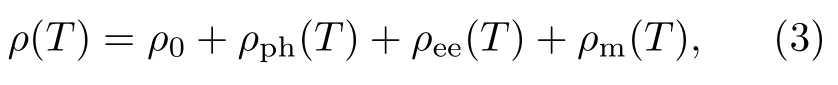
其中，ρ0为剩余电阻率，ρph（T）为电子-声子散射引起的电阻率，ρee（T）为电子-电子散射引起的电阻率，ρm（T）为无序的局域磁矩引起的电阻率。一般而言，电子-声子散射在高温时占主导。当温度T≥θD（θD为德拜温度），ρ随温度的变化关系为ρph（T）∝T，当温度T≤θD时，ρ随温度的变化关系为ρph（T）∝T5。在低温区域，电子-声子散射被冻结，主要是电子-电子散射起作用，ρ随温度的变化关系为ρee（T）∝T2。无序的局域磁矩对ρ的贡献是在整个温度范围内都很重要的，此时的ρ随温度的变化关系对于铁磁耦合为ρm（T）∝T2，而对于反铁磁耦合随温度的变化则表现为T5和T4关系［27］。在不同的温度范围内，不同的散射机制所起的主导作用不同，利用式（3）在2∼305 K的温度范围内不能对实验数据进行很好的拟合。通过拟合发现在低的温度范围内，电阻率随着温度的变化关系满足T2关系［24，25］。可见在低温度范围内，对多晶Fe4N薄膜的电阻率的贡献来自于电子-电子相互作用和/或无序的局域磁矩引起的散射。在较高的温度范围内，电阻率随着温度的变化满足Tn关系，其中n小于1，并且随着温度的升高，曲线的斜率越来越小，说明在高温度范围内，对多晶Fe4N薄膜的电阻率的贡献主要来自于电子-声子散射。总而言之，在不同厚度的多晶Fe4N薄膜中，电阻率是由多种散射机制共同作用引起的，在不同的温度范围内，不同的散射机制起着主导作用［24，25］。

图11.玻璃基底上不同厚度的多晶Fe4N薄膜的电阻率随温度的变化曲线。插图为室温电阻率随薄膜厚度的变化曲线［24，25］

为了进一步研究外加磁场对多晶Fe4N薄膜电输运特性的影响，我们测量了不同温度下的磁电阻MR。测量MR时，外加磁场平行于薄膜表面，最大外加磁场为50 kOe。图12给出了不同厚度的多晶Fe4N薄膜的MR-H曲线［24，25］。从图12（a）看出，5 nm的Fe4N薄膜，在5∼200 K的温度范围内，当磁场在0∼±500 Oe左右的范围内时，MR随着磁场的增加呈现出急剧增大的趋势。当磁场的绝对值大于500 Oe时，温度为5∼100 K时，MR随着磁场的增加呈现出缓慢的继续增大的趋势，当外加磁场达到最大值50 kOe也未达到饱和。当温度大于100 K时，MR随着磁场的增加呈现出减小的趋势，为负磁电阻［24，25］。图12（b）为10 nm的Fe4N薄膜，在5∼200 K的温度范围内，在0∼±500 Oe左右的磁场范围内，MR随着磁场的增加呈现出急剧增大的趋势。当磁场的绝对值大于500Oe时，温度为5∼40 K时，MR随着磁场的增加呈现出缓慢的继续增大的趋势，在最大的外场50 kOe下也未达到饱和。温度大于40 K时，MR随着磁场的增加呈现减小的趋势，为负的磁电阻［24，25］。对于厚度为26至163 nm的Fe4N薄膜，在零磁场附近500 Oe左右的磁场范围内，在所有温度下，薄膜的MR随着磁场增加而急剧的增大。当磁场的绝对值大于500 Oe，在温度为5、10和20 K时，MR随着磁场的增加而继续增大，最大外加磁场下也未达到饱和。而当温度大于等于30 K时，MR随着磁场的增加而减小，表现为负的磁电阻。通过上面的结果可以看出，MR随着薄膜厚度的变化，没有一定的规律，但是对于不同厚度的多晶Fe4N薄膜而言，在低温下，MR都是随着磁场的增加而增大，在较高的温度下，MR随着磁场的增加先增大然后减小为负的值。而且MR的数值几乎都小于1.2%。上述不同厚度的多晶Fe4N薄膜的MR在不同温度下随着磁场的变化呈现出了复杂的变化行为。造成这种复杂的MR变化行为的是多种散射机制引起的正MR与负MR相互竞争的结果。其中由于洛仑兹力的存在使得Fe4N薄膜的MR为正的［24，25］。因为载流子在传导的过程中会受到洛仑兹力的影响，而作螺旋运动，从而使得其受到散射的几率增大，平均自由程减小，引起电阻随着磁场的增加而增大。而随着磁场的增加，磁场提供的铁磁有序抑制了自旋波的无序散射，使得MR为负的。同时外磁场引起自旋向上和自旋向下的能带发生劈裂，使得Fe4N薄膜的s电子散射到d态的几率减小，也会引起负的MR。由于引起Fe4N薄膜磁电阻变化的物理机制在不同的温度和磁场所起的主导作用不同，导致磁电阻随着磁场和温度的变化呈现出复杂的变化行为。在低的温度和磁场下，由于洛仑兹力引起的正MR起主导作用，所以随着磁场的增加，MR呈现出快速增大的趋势。随着磁场的不断增加，磁场提供了铁磁有序同时抑制了由自旋波激发引起的电子散射和局域磁各向异性，使得MR减小，所以Fe4N薄膜的MR随着磁场增加呈现出相对于低场下的MR平缓的增大趋势；在高的温度下，薄膜MR随着磁场的增加，呈现出先增大，后减小的趋势。这主要是由于随着磁场的增加，磁场抑制自旋的无序散射引起的负MR，能带劈裂引起的负MR逐渐竞争过了由洛仑兹力导致的正MR引起的［24，25］。

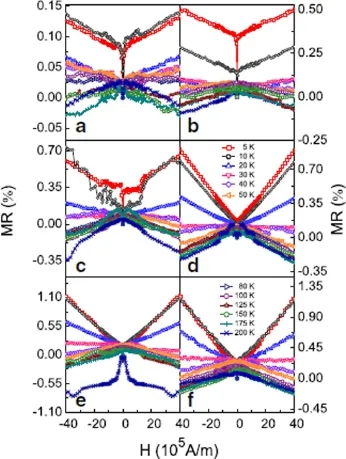
图12.玻璃基底上多晶Fe4N薄膜的MR-H曲线，薄膜厚度分别为（a）5、（b）10、（c）26、（d）58、（e）91和（f）163 nm［24，25］

IV.外延Fe4N薄膜的结构与物性

本节我们将重点介绍外延Fe4N薄膜的表面形貌、晶体结构、磁性质、电输运特性和磁电阻效应［23，24］。

A.外延Fe4N薄膜的结构

在单晶基底上制备出外延薄膜，必须要知道薄膜和基底之间的晶格失配度，只有失配度在一定范围内才能制备出外延薄膜，下面是薄膜晶格与基底晶格失配度的计算公式［24，25］

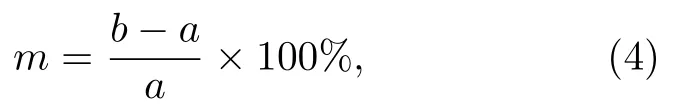
其中，m为晶格失配度，a和b分别为基底和外延薄膜的晶格常数。通常情况下，当m≤15%时，才能在单晶基底上制备出外延薄膜。由Fe4N相的晶格常数为3.795˚A，首先选择了和Fe4N晶格失配度分别为0%、-3%和-10%的LaAlO3、SrTiO3和MgO（100）取向的基底来制备外延Fe4N薄膜。我们在450◦C的MgO（100）、SrTiO3（100）和LaAlO3（100）基底上制备了氮化铁薄膜Fe4N薄膜的条件是：氮气和氩气的流量分别为20 sccm和100 sccm，溅射压强为1 Pa，溅射电压为1175 V。通过控制溅射时间制备了不同厚度的Fe4N薄膜。

图13给出了不同厚度Fe4N薄膜的原子力显微镜图像（AFM）［23，24］。从图上可以看出，5 nm厚的薄膜上有很多小洞，并且薄膜的深度与薄膜的厚度一样，说明尚未完全形成连续的薄膜。当厚度为26 nm时，薄膜表面平整。随着薄膜表面继续增加，表面出现很多小岛，并且表面粗糙度增加［23，24］。

图14给出了MgO（100）基底和在MgO（100）基底上的不同厚度的Fe4N薄膜的X射线θ-2θ扫描图［23，24］。从图中可以看出，除了MgO基底的（200）和（400）衍射峰外，不同厚度的氮化铁薄膜的衍射峰都是在23.45◦左右的Fe4N的（100）衍射峰和47.97◦左右的Fe4N的（200）衍射峰。由此可见，在单晶MgO（100）基底上制备出了取向生长的单相Fe4N薄膜。随着薄膜厚度从163 nm减小到5 nm时，Fe4N薄膜的衍射峰对应的峰位逐渐向高角度移动，并且衍射峰的强度逐渐变弱，衍射峰的半高宽的宽度逐渐变大。衍射峰向大角度偏移，这主要是由薄膜受到拉应力导致的［23，24］。MgO（100）基底的晶格常数是4.21˚A，大于Fe4N的晶格常数3.79 ˚A，所以Fe4N的（h00）面要受到面内的拉应力，引起（h00）面之间的面间距d变小，根据布拉格衍射公式可知对应的衍射角往大角度偏移。衍射峰的强度随着薄膜厚度从厚变薄而逐渐变弱，这主要是因为随着薄膜厚度逐渐变薄，对X射线的衍射级数就会减少，接收到的信号就会变弱，最后形成弱的衍射峰。随着薄膜厚度逐渐变薄，薄膜衍射峰的半高宽宽度逐渐增大，根据谢乐（Scherrer）公式可以得出，Fe4N薄膜垂直膜面的晶粒尺寸逐渐减小［23，24］。

图13.外延Fe4N薄膜的AFM图像，膜厚为（a）5、（b）25、（c）58、（d）91 nm［23，24］

我们选择了晶格常数与Fe4N晶格常数失配度分别约为-10%的MgO（100）基底、-3%的SrTiO3（100）基底、0%的LaAlO3（100）基底来制备单相外延Fe4N薄膜。图15给出了在三种基底上制备的厚度为163 nm的单相Fe4N薄膜的X射线θ-2θ扫描图［23，24］。从图中可以看出，随着薄膜晶格常数与基底晶格常数失配度的减小，Fe4N（100）和（200）衍射峰与基底的衍射峰逐渐靠近，尤其是LaAlO3（100）基底上的Fe4N薄膜的衍射峰与基底的衍射峰基本上是重合的。同时为了研究不同取向Fe4N薄膜的磁学性质和电输运特性的不同，我们还在SrTiO3（110）取向的基底上制备了Fe4N薄膜。图16（a）给出了在450◦C的SrTiO3（110）基底上的厚度为91 nm的Fe4N薄膜以及SrTiO3（110）基底的X射线θ-2θ扫描图［23，24］。当薄膜厚度为91 nm时，除了SrTiO3基底的（110）和（220）衍射峰外，只在2θ=70.18◦的地方出现了Fe4N的（220）衍射峰。图16（b）给出了SrTiO3（110）基底的X射线θ-2θ扫描图，从图中可以看出，除了基底的（110）和（220）衍射峰外，还出现了很多其它小的凸起，进一步说明图16（a）中出现的小峰来自于基底。厚度为91 nm的Fe4N薄膜是取向生长的，需要进一步的结构表征来验证是否为外延生长的［23，24］。

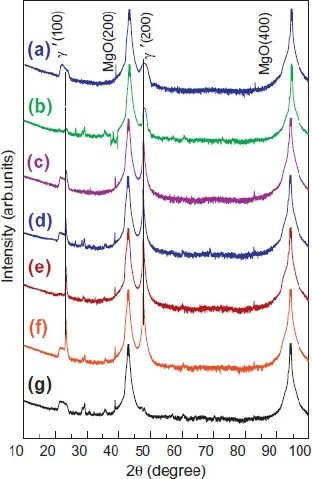
图14.MgO（100）上Fe4N薄膜的X射线θ-2θ图，膜厚为（a）5、（b）10、（c）26、（d）58、（e）91、（f）163 nm和（g）MgO（100）基底［23，24］

图15.不同单晶基底上163 nm的Fe4N薄膜的X射线θ-2θ图，（a）MgO（100）、（b）SrTiO3（100）和（c）LaAlO3（100）［23，24］

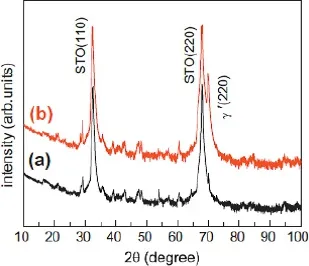
图16.SrTiO3（110）上氮化铁薄膜的X射线θ-2θ扫描图，薄膜厚度分别为（a）91 nm、（b）SrTiO3（110）基底［23，24］

已知制备在LaAlO3（100）、SrTiO3（100）、SrTiO3（110）和MgO（100）取向的单晶基底上的Fe4N薄膜都表现出了取向生长。为了证明制备在这些单晶基底上的Fe4N薄膜是外延生长的模式，对制备在MgO（100）和SrTiO3（100）、SrTiO3（110）取向的单晶基底上的Fe4N薄膜进一步的进行了X射线的φ扫描和极图的结构表征。因为LaAlO3（100）基底的晶格常数与Fe4N薄膜的晶格常数几乎是相等的，所以从X射线的θ-2θ衍射图上已无法区分衍射峰是来自基底还是薄膜，对其做X射线的φ扫描和极图的结构表征也无法区分是来自基底的还是薄膜的峰。图17给出了在MgO（100）基底上制备的厚度分别为5、10、58和163 nm的取向生长的Fe4N薄膜的X射线φ扫描图［23，24］。为了避开MgO（100）基底的衍射峰的影响，把2θ衍射角固定于41.22◦，因为在41.22◦这个角度，MgO（100）基底是没有衍射峰出现的，在这个角度只有Fe4N薄膜的（111）衍射峰。测量时样品的旋转范围是：α=35.26◦，β=-180◦∼+180◦。从图中可以看出，不同厚度的Fe4N薄膜的X射线φ扫描图中在360◦的范围内都出现了四个比较尖锐的等间隔（间隔为90◦）的衍射峰，这四个衍射峰来自于具有C4旋转对称的Fe4N（111）面的衍射，表现出四重对称性。随着Fe4N薄膜厚度的增加，衍射峰的强度增强，这是因为随着薄膜厚度的增加，薄膜中参与X射线衍射的晶面越来越多，所以衍射峰的强度增强，但是并不会影响到Fe4N薄膜的四重对称性。所以，MgO（100）基底上的取向生长的Fe4N薄膜具有立方外延结构，Fe4N薄膜与MgO（100）基底的外延生长关系为［23，24］：Fe4N（100）［001］∥MgO（100）［001］。图18给出了SrTiO3（100）和SrTiO3（110）基底上厚度分别为163和91 nm的取向生长的单相Fe4N薄膜的X射线φ扫描图，其中2θ衍射角对应固定于Fe4N（111）的峰位处，即：2θ=41.22◦［23，24］。如图18（a）所示，为SrTiO3（100）基底上取向生长的Fe4N薄膜的X射线φ扫描图，当φ转过360◦后，φ扫描图中出现了四个比较尖锐的等间隔（间隔为90◦）的Fe4N薄膜的衍射峰，这四个衍射峰来自于具有C4旋转对称的（111）面，说明Fe4N薄膜具有面内的立方对称性，则Fe4N薄膜与SrTiO3（100）基底的外延生长关系可表示为：Fe4N（100）［001］∥SrTiO3（100）［001］［23，24］。图18（b）给出了SrTiO3（110）基底上取向生长的Fe4N薄膜的X射线φ扫描图，当φ转过360◦后，φ扫描图中出现了二个比较尖锐的等间隔（间隔为180◦）的Fe4N薄膜的衍射峰，说明薄膜具有面内的立方对称性，取向生长的Fe4N薄膜与SrTiO3（110）基底的外延生长关系可表示为Fe4N（110）［110］∥SrTiO3（110）［110］［23，24］。为了进一步的表征Fe4N薄膜在单晶基底上的外延生长，我们分别测量了MgO（100）和SrTiO3（100）单晶基底上制备的厚度为163 nm的Fe4N薄膜的极图。图19给出了MgO（100）和SrTiO3（100）单晶基底上制备的163 nm的外延Fe4N薄膜的平面极图和三维极图，很好的反映了Fe4N薄膜的四重对称性，进一步证明了Fe4N薄膜在单晶基底上的外延生长模式。图20给出了SrTiO3（110）基底上的厚度为91 nm的外延Fe4N薄膜的平面极图和三维极图，也很好的证明了薄膜的外延生长特性。X射线θ-2θ衍射结合φ扫描图和极图的结构表征，证明了Fe4N薄膜的外延生长模式［23，24］。

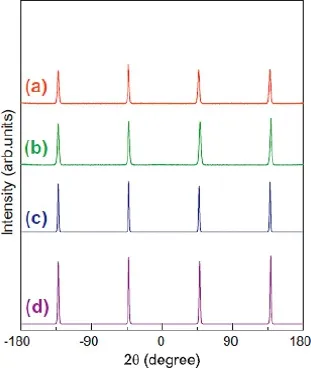
图17.MgO（100）上Fe4N薄膜的X射线φ扫描图，薄膜厚度分别为（a）5、（b）10、（c）58和（d）163 nm［23，24］

B.外延Fe4N薄膜的磁性

图21给出了MgO（100）基底上不同厚度的外延Fe4N薄膜的室温面内磁滞回线［23，24］。从磁滞回线的形状可以看出，不同厚度的外延Fe4N薄膜呈现出软磁性。插图给出的是薄膜的饱和磁化强度Ms和Hc随着薄膜厚度的变化关系曲线。当薄膜厚度从5 nm增加到10 nm时，薄膜的Ms从1213 emu/cm3增加到1243 emu/cm3，随着薄膜厚度增大到58 nm，Ms几乎线性的减小到最小值1056 emu/cm3，当薄膜的厚度为91 nm时，Ms有最大值1341 emu/cm3。当薄膜的厚度增大到163 nm时，Ms又减小到1181 emu/cm3。可见外延Fe4N薄膜的厚度会影响到它的Ms的大小，但是Ms随着厚度变化没有很强的规律性［23，24］。从外延Fe4N薄膜的矫顽力Hc随着薄膜厚度的变化关系曲线可以看出，外延Fe4N薄膜的Hc不随薄膜厚度的变化而变化，基本保持在50 Oe左右。影响薄膜Hc大小的因素有很多，如薄膜受到的应力大小、薄膜的表面粗糙度、颗粒尺寸的大小等，在MgO（100）基底上制备的外延Fe4N薄膜的Hc随着厚度变化基本保持不变，可能就是上面提到的这些诸多的因素综合影响造成的［23，24］。

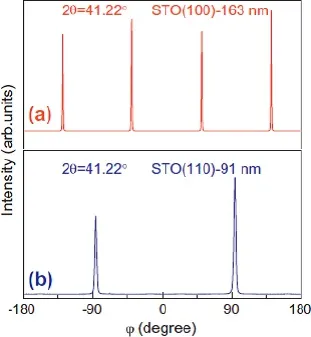
图18.Fe4N（100）和（110）薄膜的X射线φ扫描图，（a）SrTiO3（100）和（b）SrTiO3（110）［23，24］

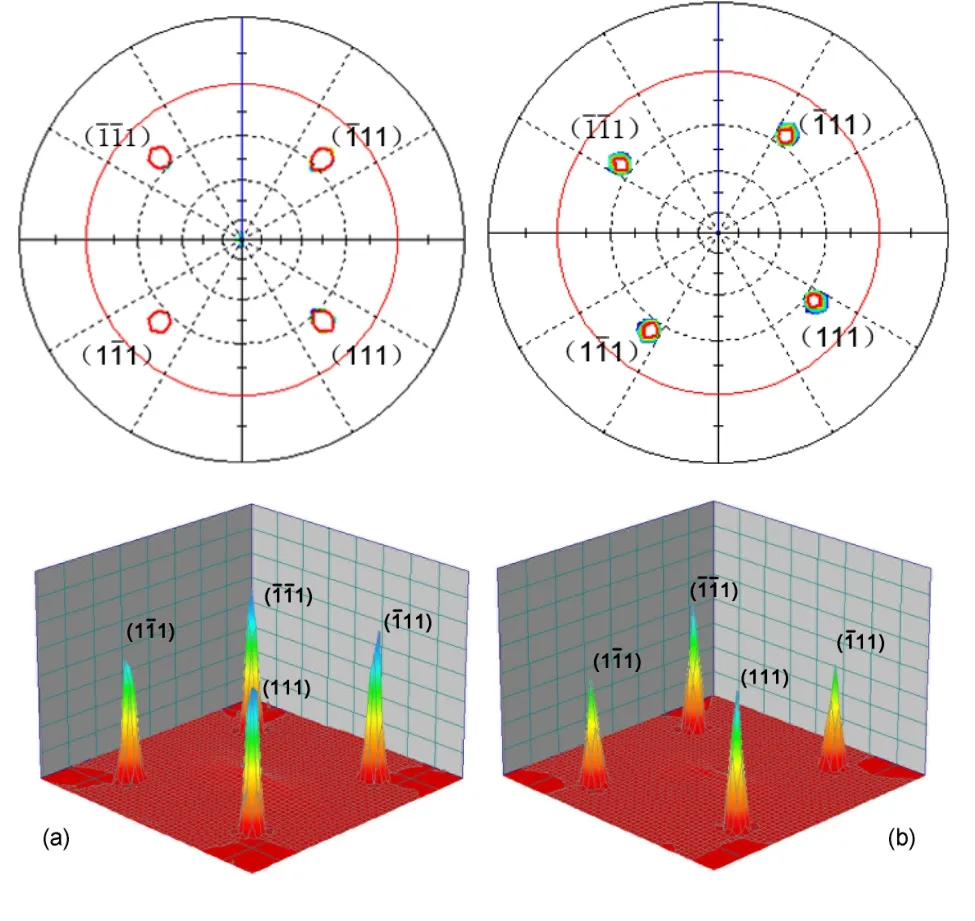
图19.MgO（100）和SrTiO3（100）上Fe4N薄膜的平面和三维极图，α=20∼90◦，步长为2.5◦，（a）MgO（100）和（b）SrTiO3（100）［23，24］

图20.91 nm外延Fe4N（110）薄膜的平面和三维极图，α=20∼90◦，步长为2.5◦［23，24］

我们还进一步测量了MgO（100）基底上不同厚度的外延Fe4N薄膜在不同温度下的磁滞回线。图22分别给出了厚度为10 nm外延Fe4N薄膜在不同温度下的磁滞回线［23，24］。从图中可以看出，磁滞回线的形状反映出了随着温度的变化，外延Fe4N薄膜呈现出软磁性。图22右下角的插图给出了外延Fe4N薄膜的Ms和Hc随着温度的变化关系曲线。Ms随着温度的升高而逐渐减小。当温度小于100 K时，Hc大小∼150 Oe，随着温度的升高，Hc减小。当温度大于100 K时，Hc减小到∼50 Oe［23，24］。

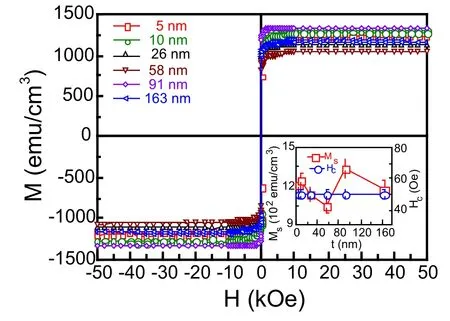
图21.MgO（100）上不同厚度的外延Fe4N薄膜的室温面内磁滞回线，插图为Ms和Hc随着薄膜厚度的变化关系曲线［23，24］

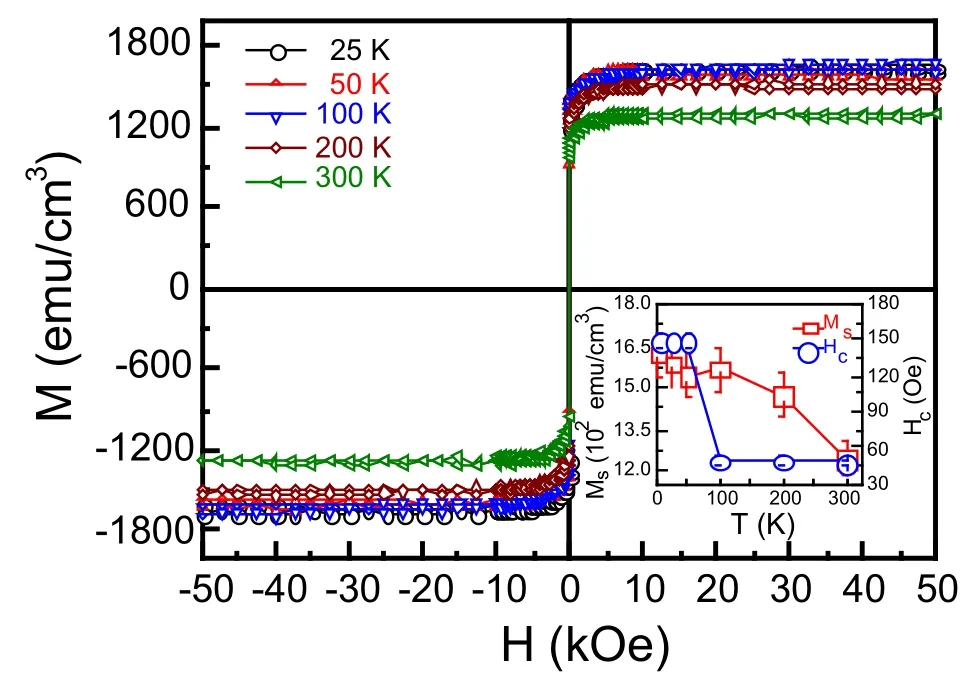
图22.MgO（100）上10 nm的外延Fe4N薄膜在不同温度下的面内磁滞回线，插图为Ms和Hc随着温度的变化曲线［23，24］

C.外延Fe4N薄膜的电输运特性

图23给出了MgO（100）基底上制备的不同厚度的外延Fe4N薄膜的ρ（T）/ρ（300 K）随着温度的变化关系曲线［23，24］。从图中可以看出，随着温度的升高，Fe4N薄膜的电阻率逐渐增大，呈现出金属的导电特性。右下角的插图给出了室温下Fe4N薄膜的ρ随着薄膜厚度的变化关系曲线。从图中可以看出，Fe4N薄膜的ρ随着薄膜厚度的减小而逐渐增大［23，24］。随着薄膜厚度的减小，薄膜受到张应力逐渐地增大，使得薄膜中的缺陷增多，并且随着薄膜厚度的减小，薄膜表面对电子的散射就会增强，所以随着Fe4N薄膜厚度的减小，ρ逐渐增大。同时，通过对比玻璃基底上制备的相同厚底的多晶Fe4N薄膜的ρ随着薄膜厚度的变化得出，相同厚度的多晶Fe4N薄膜的室温ρ大于外延Fe4N薄膜的室温ρ，这主要是由于相对于外延薄膜，多晶薄膜中存在着更多的缺陷杂质和颗粒边界，引起薄膜ρ的增大。图24给出了不同基底上的厚度为10 nm的Fe4N薄膜的ρ（T）/ρ（300 K）随着温度的变化关系曲线［23，24］。薄膜的电阻率随着温度的降低而减小，呈现出金属的导电特性。右下角的插图给出了不同基底上制备的Fe4N薄膜的室温ρ。LaAlO3（100）基底上的ρ最小，玻璃基底上的ρ最大。由于玻璃基底上制备的是多晶的Fe4N薄膜，与单晶基底上制备的外延Fe4N薄膜相比较存在更多的颗粒边界和缺陷，所以会引起ρ增大。由于LaAlO3（100）基底的晶格常数与Fe4N薄膜的晶格常数几乎相等，所以在LaAlO3（100）基底上制备的Fe4N薄膜中的缺陷相对而言就会很少，在低温下Fe4N薄膜的ρ相对在MgO（100）和SrTiO3（100）基底上制备的Fe4N薄膜的ρ就要小些。图26给出了SrTiO3（100）和（110）基底上制备的Fe4N薄膜的ρ（T）/ρ（300 K）随着温度的变化关系曲线［23，24］。随着温度的升高，不同取向的SrTiO3基底上制备的Fe4N薄膜的电阻率都逐渐增大，表现出金属的导电特性。右下角的插图给出了不同取向的SrTiO3基底上的Fe4N薄膜的室温ρ。随着温度的升高，不同取向的SrTiO3基底上的Fe4N薄膜的电阻率大小关系为：ρ（110）＞ρ（100）。可见Fe4N薄膜的ρ沿着薄膜的不同生长取向是不同的。这主要是因为在Fe4N薄膜的不同取向上，Fe原子和氮原子的占位不同，使得电子云的分布不同，进而影响到Fe4N薄膜不同取向的ρ大小不同［23，24］。

图26给出了MgO（100）基底上不同厚度的外延Fe4N薄膜的MR-H曲线［23，24］。图4-23（a）和（b）给出了厚度分别为5 nm和10 nm的Fe4N薄膜的MR在不同温度下随磁场的变化曲线。在较低的温度下，MR随着磁场的增加而增大，当温度高于30 K时，MR随着磁场的增加而减小，呈现出负的MR。随着Fe4N薄膜的厚度增加到26和58 nm，在低的温度下，MR随着磁场的增加先有一个小的减小然后又增大。在较高的温度下，MR随着磁场的增加而减小，表现为负的MR。为了对比不同基底上制备的Fe4N薄膜的MR的变化关系，我们测量了不同基底上厚度为10 nm的Fe4N薄膜的MR［23，24］。如图27给出了在MgO（100）、SrTiO3（100）、LaAlO3（100）单晶基底和玻璃基底上制备的厚度为10 nm的Fe4N薄膜的MR-H曲线。从图中可以看出，无论是单晶基底上制备的外延Fe4N薄膜还是玻璃基底上制备的多晶Fe4N薄膜，除了零场附近MR随着磁场的增加变化不同外，在较低的温度下，MR随着磁场的增加而增大并且在最大的磁场下也未达到饱和。当温度高于30 K时，MR随着磁场的增加而减小，呈现出负的MR。在零场附近，对于四种基底上制备的Fe4N薄膜而言，随着磁场的增加，MR在不同的温度下表现为有的先增大再减小，有的一直增大，有的一直减小的行为。并且在同一个温度下，单晶基底上的Fe4N薄膜的MR要比玻璃基底上的大［23，24］。图28给出了SrTiO3基底上的不同取向的Fe4N薄膜的MR-H曲线。从图中可以看出，在不同取向的SrTiO3基底上的Fe4N薄膜的MR随着磁场的变化表现出相似的行为，都是在低的温度下，MR随着磁场的增加而增大，当温度大于30 K时，MR随着磁场的增加而减小为负值。其中在（100）取向上的MR大于在（110）取向上的MR［23，24］。上面介绍的是Fe4N薄膜的MR随着温度和磁场的变化关系。无论是同一基底上不同厚度的Fe4N薄膜的MR变化规律，还是不同基底上相同厚度的Fe4N薄膜的MR变化规律，基本上都是相似的。通过对比可以得出，无论是多晶还是外延Fe4N薄膜，MR产生的原因是相同的。随着温度的降低，Fe4N薄膜的电阻率减小，使得MR增大。随着温度的升高，当外加磁场使得Fe4N薄膜中的铁磁有序化和由自旋波引起的电子散射和局域磁各向异性受到抑制，从而使得MR随着磁场的增大而减小。根据s-d能带散射模型，外加磁场会使得多数自旋能带和少数自旋能带发生劈裂，产生负的MR。这几种机制在不同的温度和磁场下相互竞争，使得MR的行为表现的复杂化［23，24］。

图23.MgO（100）上不同厚度的外延Fe4N薄膜的电阻率随温度的变化曲线，插图为室温电阻率随薄膜厚度的变化曲线［23，24］

图24.不同基底上10 nm的Fe4N薄膜的电阻率随温度的变化，插图为室温电阻率［23，24］

图25.SrTiO3（100）和（110）基底上10 nm的Fe4N薄膜的电阻率随温度的变化关系曲线，插图为室温下的电阻率［23，24］

人们也常用各向异性磁电阻AMR来研究铁磁性材料的电输运特性。AMR效应一般存在于铁磁金属及其合金材料中，电阻率ρ的大小与磁化强度方向和电流的方向之间的夹角有关系。从20世纪90年代初期，AMR效应就已经用于硬盘驱动器的磁记录读出磁头。1857年，汤姆逊首先在铁磁金属中发现AMR效应［28］。本节中AMR的定义为［29］

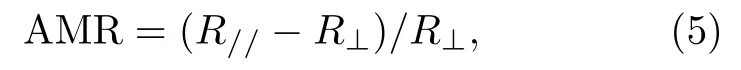
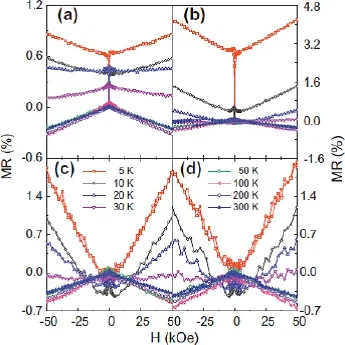
图26.MgO（100）上Fe4N薄膜的MR-H曲线，膜厚为（a）5、（b）10、（c）26和（d）58 nm［23，24］

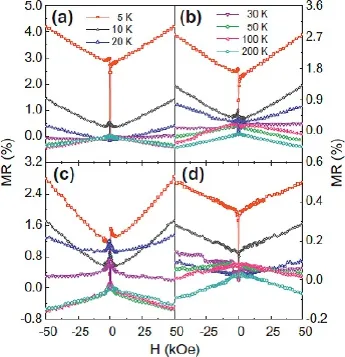
图27.10 nm的Fe4N薄膜的MR-H曲线，（a）MgO（100）、（b）SrTiO3（100）、（c）LaAlO3（100）和（d）Glass［23，24］

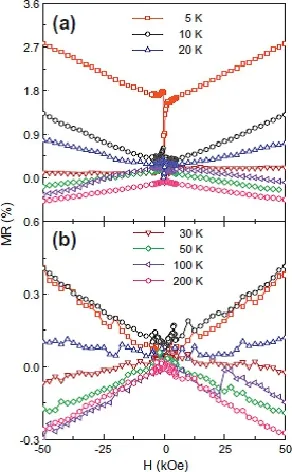
图28.不同取向的外延Fe4N薄膜的MR-H曲线，（a）（100）和（b）（110）［23，24］

其中R//和R⊥分别为磁化方向与电流方向平行和垂直时薄膜的电阻。图29给出了MgO（100）基底上制备的不同厚度的外延Fe4N薄膜在外加磁场为10 kOe时不同温度下的AMR的变化极图。从图中可以得出，不同厚度的Fe4N薄膜的AMR表现出两重对称性，并且AMR的数值为负的。随着温度从5 K升高到300 K的过程中，AMR的两重对称性逐渐减弱。随着薄膜厚度的变化，外延Fe4N薄膜的AMR也发生了变化。当薄膜厚度为5 nm时，Fe4N薄膜最大的AMR值约为-1.7%。当薄膜厚度为26 nm时，Fe4N薄膜具有最大的AMR，约为-4.2%。厚度为10和58 nm的Fe4N薄膜的AMR分别约为-3.4%和-3.7%。随着温度的升高，不同厚度的外延Fe4N薄膜的AMR的绝对值减小，当温度为300 K时，AMR接近于零。随着Fe4N薄膜厚度的增加，不同温度下的AMR的绝对值增大［23，24］。图30给出了MgO（100）基底上不同厚度的外延Fe4N薄膜在5和300 K下的AMR随着磁场的变化关系曲线。其中图的左边对应着在5 K下的AMR随着磁场的变化关系曲线，右边对应着在300 K下的AMR随着磁场的变化关系曲线。从图中可以看出在5 K下测得的AMR除了在200 Oe下表现出不同的形状外，随着磁场从50 kOe变化到500 Oe，AMR都呈现出两重对称性。在200 Oe的磁场下得到的AMR的形状类似于梯形，在峰的顶部变得很平缓，偏离了余弦波函数的形状。可以看出，随着磁场的逐渐减小，AMR的形状从余弦波的形状逐渐过渡到类似于梯形的形状。而且，AMR数值为负值，并且AMR的大小基本不随磁场的变化而改变［23，24］。随着薄膜厚度的变化，AMR的数变化不大，只有在薄膜厚度为5 nm时，样品的AMR比较小，仅约-1.7%。其余不同厚度的Fe4N薄膜的AMR值均在-4%左右。从300 K下测量得到的不同厚度的Fe4N薄膜的AMR可以看出，不同薄膜厚度和磁场下测得的AMR都呈现出两重对称性［23，24］。AMR为负值，随着磁场的变化，AMR的数值基本也是不变的。但是数值很小，都小于-0.2%。随着外加磁场从50 kOe减小到100 Oe，300 K下Fe4N薄膜的AMR的形状逐渐从余弦形状过渡到峰的顶部比较平坦的形状。造成低磁场下Fe4N薄膜的AMR有别于高磁场下的特殊的形状的原因，目前还没有给出一个合理的解释，可能与小的外加磁场不足以使Fe4N薄膜磁化到饱和有关［23，24］。

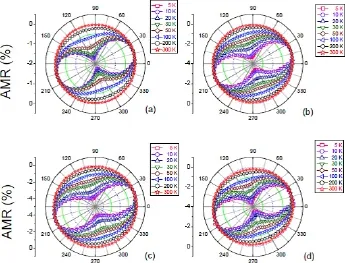
图29.MgO（100）上Fe4N薄膜在10 kOe下的AMR极图，电流方向沿着［001］，膜厚分别为（a）5、（b）10、（c）26和（d）58 nm［23，24］

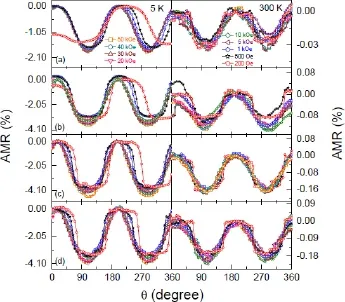
图30.5和300 K下MgO（100）上的Fe4N薄膜的AMR曲线，电流沿着［001］，膜厚为（a）5、（b）10、（c）26和（d）58 nm［23，24］

为了进一步研究不同基底上的Fe4N薄膜的AMR的特点，图31给出了在10 kOe的磁场下不同温度下测量的不同基底上的γ′-Fe4N薄膜的AMR的极图。从图中可以看出，在不同的基底上的Fe4N薄膜的AMR均呈现出两重对称性，随着温度的升高，AMR的两重对称性减弱。在三种单晶基底MgO（100）、SrTiO3（100）和LaAlO3（100）上制备的γ′-Fe4N薄膜的AMR值最大分别达到了-3.45%、-3.47%和-3.56%。在玻璃基底上制备的多晶Fe4N薄膜的AMR值相对于单晶基底上的要小很多，最大只有约-0.89%。随着温度的升高，不同基底上的Fe4N薄膜的AMR的绝对值都减小，尤其是玻璃基底上的Fe4N薄膜的AMR的绝对值在整个温度范围内都小于1%，单晶基底上的Fe4N薄膜的AMR的绝对值都大于玻璃基底上的，LaAlO3（100）基底上的Fe4N薄膜的AMR在各温度下都是最大的［23，24］。

图32给出了SrTiO3（100）和SrTiO3（110）基底上的Fe4N薄膜在10 kOe的磁场下的AMR随着温度的变化曲线［23，24］。从图中可以看出，不同取向的基底上的Fe4N薄膜的AMR在不同的温度下都呈现出了很好的两重对称性，除了SrTiO3（110）基底上的Fe4N薄膜在300 K下测得的AMR不具有两重对称性［23，24］。不同取向的SrTiO3基底上的Fe4N薄膜的AMR值均为负值，并且在低温时AMR达到最大值。SrTiO3（100）和SrTiO3（110）基底上的Fe4N薄膜的AMR最大值分别为-3.47%和-1.06%［23，24］。

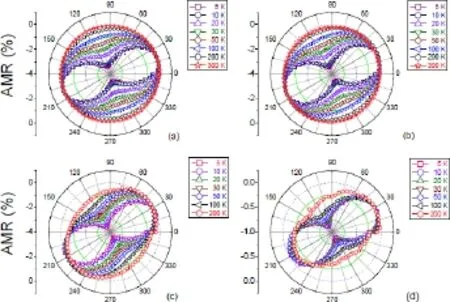
图31.10 kOe下不同基底上γ′-Fe4N薄膜的AMR，（a）MgO（100）、（b）SrTiO3（100）、（c）LaAlO3（100）和（d）Glass［23，24］

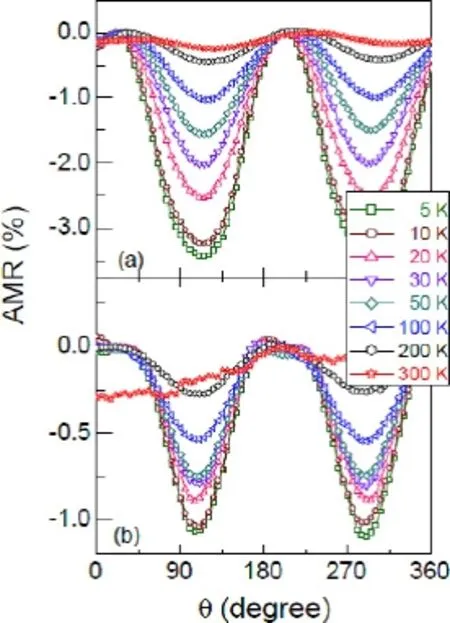
图32.10 kOe下变温度测量的不同取向SrTiO3上外延γ′-Fe4N薄膜的AMR，电流方向沿着［001］，（a）（100）和（b）（110）［23，24］

V.Fe4N/CoN双层膜的结构与物性

本节我们将重点介绍Fe4N/CoN双层膜的表面形貌、晶体结构、磁性质、电输运特性和磁电阻效应［30，31］。

A.外延Fe4N/CoN双层膜的的结构

图33给出了不同铁磁层厚度的Fe4N（tFe4N）/ CoN（8 nm）双层膜的表面形貌，tFe4N=4、6、8、10、12、20 nm［30，31］。样品的表面粗糙度在0.164∼0.219 nm范围内，表明长在Fe4N之上的CoN薄膜表面较平坦。同时，也证实了不同厚度的Fe4N薄膜是连续的，相对较平滑的。每个样品的表面起伏呈现在图33的插图中，双层膜的表面起伏波动不超过0.6 nm［30，31］。

图34给出了MgO（100）基底、Fe4N单层膜以及Fe4N/CoN双层膜的X射线θ-2θ扫描图［30，31］。对于单层Fe4N薄膜，只有（100）、（200）峰出现，表明薄膜沿c轴取向生长。从Fe4N/CoN双层膜的XRD图中可以看出，在Fe4N（200）晶面上生长了CoN（111）面。Fe4N的晶格常数为3.795˚A，而CoN的晶格常数为4.297˚A，晶格失配度高达13%。因此，相应于CoN（111）六角面的矩形网格来匹配Fe4N（200）晶面的矩形网格。这样的晶格匹配类似于FePt（100）/CoO（111）双层膜［32］，在Ir（001）基底上生长的CoO（111）也具有同样的晶格匹配［33］。

为了进一步证实薄膜的外延关系和平面对称性，对样品做了φ扫描。选用Fe4N（111）面，固定X射线在α=35.3◦，2θ=41.22◦，这个角度没有CoN和MgO基底的峰。从图35（b）中可以看到四重对称的衍射峰，反映出Fe4N的立方结构和C4旋转对称性。对于CoN（200）面的φ扫描，固定X射线在α=35.3◦，2θ=42.02◦，这个角度可以避开Fe4N（111）和MgO（200）的峰，仍然看到了四重对称峰，因此长在Fe4N上的CoN（111）面保持矩形状，而非六角。X射线的θ-2θ扫描和φ扫描结果表明Fe4N/CoN双层膜呈现外延生长，具体的外延关系为：MgO（100）||Fe4N（100）||CoN（111）和MgO

图35为Fe4N/CoN双层膜的透射电子显微镜图像［30，31］。从图36（a）中可以得到Fe4N和CoN的厚度分别为8 nm，与台阶仪测得的结果相符。图35（b）反映出两个清晰的界面，包括基底MgO和Fe4N的界面以及Fe4N和CoN的界面。插图中相应的快速傅里叶变换图像呈现出Fe4N和CoN的晶格结构，Fe4N（200）面的衍射斑点位于CoN（111）面的衍射斑点的正上方，证实了双层膜的外延生长关系。

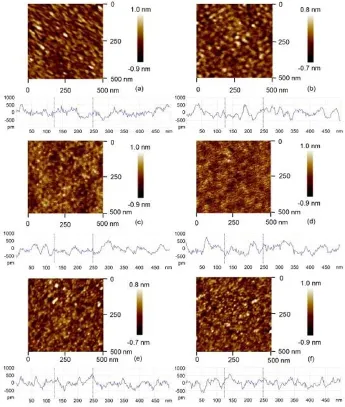
图33.不同Fe4N厚度的Fe4N/CoN（8 nm）双层膜的表面形貌以及纵向起伏，（a）4、（b）6、（c）8、（d）10、（e）12、（f）20 nm［30，31］

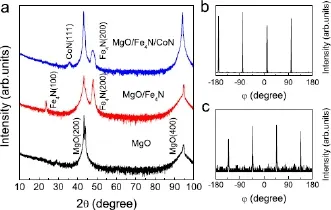
图34.（a）MgO（100）、Fe4N单层膜和Fe4N/CoN的X射线θ--2θ图，（b）Fe4N（111）的φ扫描，（c）CoN（200）的φ扫描［30，31］

图35.Fe4N（8 nm）/CoN（8 nm）双层膜的透射电子显微镜图像，（a）低分辨图，（b）高分辨图，插图为选区电子衍射图［30，31］

B.外延Fe4N/CoN双层膜的的磁性

图36为Fe4N（8 nm）/CoN（8 nm）双层膜在不同温度下的磁滞回线。HC1和HC2分别为磁滞回线左右两端的矫顽力场。HC1的值随着温度的增加不断减小，而HC2的值在低于50 K缓慢增加，高于50 K快速减小。交换偏置场定义为［30，31］

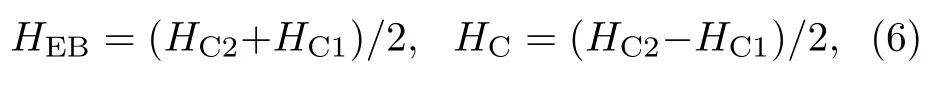
为了得到交换偏置HEB和矫顽力HC随温度的变化关系，我们从磁滞回线中提取出HEB和HC，如图37和38所示。加50 kOe的磁场冷却到3 K之后，交换偏置为-105 Oe，随着温度的增加，交换偏置逐渐减小［30，31］。可是，到8 K时，交换偏置变为正值。随着温度的继续增加，到20 K达到正的最大值33 Oe，甚至到350 K仍然保持25 Oe［30，31］。交换偏置随温度的变化较复杂，不同于一般的交换偏置特征。首先，我们需要排除单层Fe4N的交换偏置。之前我们组报道过在铁的氮化物中存在交换偏置［34］，但是这一铁的氮化物是混合相，包括许多不同的相，比如FeN、Fe2N、Fe3N等，这些相彼此耦合，尤其是在晶界处被钉扎的磁矩的直接耦合，造成了铁的氮化物中交换偏置的发生。在多晶和外延Fe4N中均没有发现交换偏置现象。Fe4N/CoN双层膜中的Fe4N为外延薄膜，已经通过XRD和TEM得到证实，在外延Fe4N中不存在交换偏置。其次，CoN应该为反铁磁性的岩盐结构，因为单层Fe4N没有交换偏置，如果CoN为顺磁性的闪锌矿结构，我们不可能观察到这样明显的交换偏置。因此，在Fe4N/CoN双层膜中观察到的交换偏置现象应该是来自于Fe4N/CoN界面的交换耦合［30，31］。

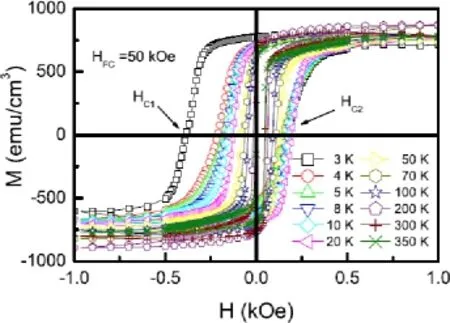
图36.Fe4N/CoN双层膜在50 kOe的场冷却之后测得的不同温度下的磁滞回线［30，31］

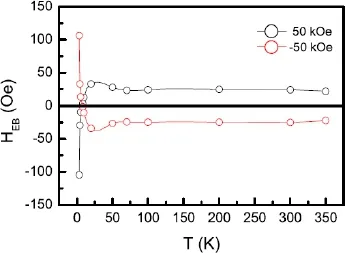
图37.Fe4N/CoN双层膜在±50 kOe的冷却场下的交换偏置随温度的变化关系［30，31］

一般来说，正的冷却场导致负的交换偏置，因为它需要更多的能量去克服铁磁/反铁磁界面的交换作用。交换偏置由于热扰动的影响会随着温度的增加逐渐减小到零，交换偏置为零的温度称为冻结温度TB［30，31］。不过，也有一些关于正交换偏置的报道。在FeF2/Fe和MnF2/Fe双层膜中，相对于较小的正冷却磁场，更大的正冷却磁场会使得交换偏置从负值转向正值［35，36］。但是我们所加的冷却磁场为50 kOe，足够大去排列反铁磁磁矩沿着冷却磁场的方向，从而在所有的温度范围产生正的交换偏置。不可能出现在低温下为负值，高温下为正值的情况。因此排除了冷却场导致正的交换偏置这一可能性［30，31］。

在-50 kOe的磁场冷却后，再次测量不同温度下的磁滞回线，得到的交换偏置如图37所示。负场冷却的结果与正场冷却的结果完全对称，交换偏置在8 K从正转向负。可是矫顽力并不受冷却磁场的影响，两种情况下得到的矫顽力均随温度的增加快速减小，并且二者的值完全相同，如图38所示［30，31］。图38的插图表明，随着冷却磁场的方向改变，磁滞回线的偏移方向也发生改变，这正好表明在这一系统中存在的交换偏置独有的单向各向异性。同时，我们还发现磁滞回线沿着磁化强度的轴线方向也发生偏移，正的冷却磁场导致向上偏移，负的冷却磁场导致向下偏移。这一纵向的磁化强度的偏移可能与Fe4N/CoN界面处的铁磁耦合相关联［37，38］。

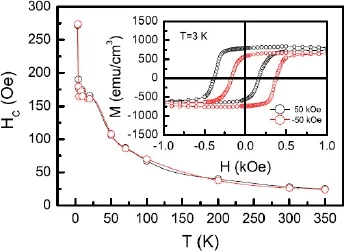
图38.Fe4N/CoN双层膜在±50 kOe的冷却场下的矫顽力场随温度的关系，插图为±50 kOe的冷却场下3 K下的磁滞回线［30，31］

由于在低温下分别测了3、4、5、8、10 K下的磁滞回线，这样小的温度间隔可能会引起磁锻炼效应，或许会造成交换偏置符号的转变。交换偏置场最初的减小可能会受到磁锻炼效应的影响。我们没有进行过专门的磁锻炼过程，在低温下，小的温度间隔可能会带来轻微的磁锻炼效应的影响，但它不是正交换偏置产生的主要因素。Mishra等［39］在NiFe/IrMn双层膜中发现磁锻炼效应可以诱导正交换偏置。在经过14次的磁锻炼过程后，磁滞回线仅仅在一个小的温度范围内朝着正场方向偏移。但是，我们没有经过磁锻炼过程，正交换偏置却保持在一个相对较大的温度范围内。并且在Cu1-xMnx/Co双层膜中，低温下温度间隔更小，也观察到正交换偏置，这一正的交换偏置并没有归结于磁锻炼效应，而是由于CuMn中的自旋玻璃态和CuMn/Co双层膜的界面耦合共同作用导致的。为了排除这一可能性，我们在3 K下连续测量了5次磁滞回线。图39给出了Fe4N/CoN双层膜的磁锻炼效应［30，31］。第一条磁滞回线显示了明显的偏移，而从接下来的四条磁滞回线可以看到交换偏置的缓慢减小，这是磁锻炼效应的典型特征。插图显示了五条磁滞回线的交换偏置场和矫顽力场随磁锻炼次数的变化。在第二次磁锻炼之后，HEB和HC减小缓慢，第五次之后，仍然表现负的交换偏置，因此可以判定正的交换偏置不是由于磁锻炼效应造成的。

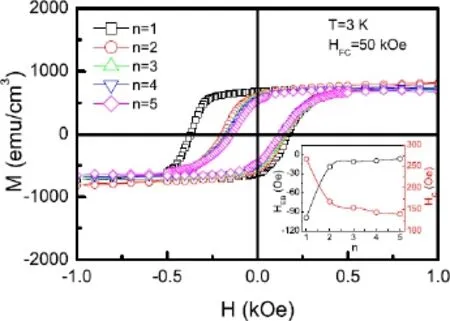
图39.Fe4N/CoN双层膜在3 K下测得的5次磁滞回线，插图为交换偏置场和矫顽力场随磁锻炼次数的变化关系［30，31］

我们采用相同的程序测量了不同Fe4N厚度和不同CoN厚度的Fe4N/CoN双层膜的磁滞回线，结果如图40所示。所有样品的交换偏置均表现出从负到正的转变，并且一直保持到350 K仍然为正。但不同的是交换偏置符号发生转变的温度不同［31，32］。在图40（a）的插图中，我们可以看到，当CoN的厚度低于10 nm时，转变温度低于20 K。可是当CoN厚度为10和12 nm时，转变温度高达200 K，而对于更厚的20 nm样品，转变温度再次降低到50 K。已有的报道中，交换偏置变为正值仅仅发生在冻结温度附近，比如Cu1-xMnx/Co和CoO/Co双层膜［40-42］。在Cu1-xMnx/Co双层膜中观察到TB附近的正交换偏置是由于在CuMn中的自旋玻璃态和CuMn/Co双层膜的界面耦合二者共同作用导致。而CoO/Co双层膜的正交换偏置则是来自于TB附近较低各向异性的反铁磁晶粒的磁无序。这两种情况都可以归结为铁磁耦合和反铁磁耦合的共存和竞争。正的交换偏置离不开反铁磁界面耦合。

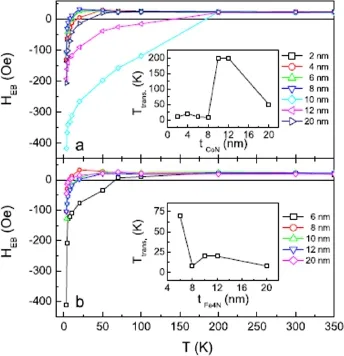
图40.Fe4N/CoN双层膜的交换偏置随温度的变化关系，（a）不同CoN厚度，（b）不同Fe4N厚度，插图为交换偏置场符号转变的温度随CoN和Fe4N厚度的变化关系［31，32］

在图40（b）的插图中，我们可以看到，随着Fe4N厚度的减小，交换偏置的转变温度呈现大致的增加趋势。这是由于在较薄的Fe4N层中，大多数的磁矩被反铁磁层钉扎在界面处，交换相互作用在低温下趋于铁磁耦合。而在高温下，反铁磁耦合占主导作用。因此，铁磁层越薄，转变温度越高［31，32］。

相似的现象在NiFe/NiO双层膜中被发现，在1 kOe的冷却场下交换偏置为负值，而当改变冷却场的方向时，交换偏置就发生了符号的转变。在30 K时，交换偏置改变符号，并且一直保持到300 K。对于这一现象，该作者认为不能用反铁磁晶粒模型来解释，因为不可能存在如此高比例的低各向异性的反铁磁晶粒。这一行为应该归结为晶粒不稳定的反铁磁排列和界面自旋玻璃态的贡献。我们的实验结果不同于上面的现象，我们的交换偏置符号的转变不依赖于冷却场的大小和方向。

总之，交换偏置从负到正的转变不是来源于磁锻炼效应，也不是来源于反铁磁晶粒，而是由于交换各向异性的改变所导致。它或许可以归因于复杂的界面自旋结构及界面处铁磁耦合和反铁磁耦合相互竞争导致的阻挫效应。

值得注意的是，在高温下所有的正交换偏置接近一个常数23 Oe。这个常数的来源可以从以下几个方面来讨论：（1）这个常数不是测量误差，通过在相同程序下测量单层Fe4N发现并不存在所谓的常数误差；（2）这个正交换偏置常数维持在高温区域（200∼350 K），甚至高于CoN的反铁磁奈尔温度。高于奈尔温度，CoN的磁矩排布无序，反铁磁各向异性消失。因此，这一常数不是来自于CoN层的钉扎效应；（3）这个值可能相关于本征的界面耦合。由于大的晶格失配，受应力的CoN薄膜长在外延Fe4N（200）面，产生了一个非六角的CoN（111）面。在Fe4N（200）面上的晶格畸变的CoN（111）使得界面耦合更强。在界面处，Fe和Co的3d态通过N的2p态间接形成反铁磁耦合，促进了本征的剩余钉扎磁矩［43］。这一耦合和CoN的反铁磁相转变无关，因此高于奈尔温度仍然存在［31，32］。

另外，还有一个有趣的现象值得去关注。随着Fe4N厚度的减小，磁滞回线逐渐变得不平滑。主要表现在Fe4N厚度为4和6 nm的双层膜中，尤其是Fe4N厚度为4 nm的双层膜。在Fe4N（4 nm）/CoN（8 nm）样品中，磁化强度表现了复杂的变化。同时，1 kOe的磁场不足以翻转全部的磁矩，因此外加磁场增加为10 kOe，不同温度的磁滞回线如图41所示［31，32］。从42（a）中可以看到，在3 K下，当磁场减小到大约0.6 kOe时，磁化强度开始增加，然后在接近于零磁场附近，磁化强度又快速减小，在负场方向也有同样的变化。在±0.6 kOe的磁场范围内，磁化强度发生不正常的翻转，并且在高温下更显著。可是单层Fe4N（4 nm）薄膜的磁滞回线并没有这种现象发生。这一不平滑的磁滞回线可能是由于在薄的Fe4N（4 nm）薄膜中各种复杂的、无序的磁结构造成的。磁畴模型或许可以解释这一现象［44］。在较厚的铁磁层中，磁化强度的翻转主要被界面的交换耦合所控制。可是，在Fe4N（4 nm）/CoN（8 nm）样品中，铁磁磁畴的颗粒尺寸很小，导致畴与畴之间的相互作用产生额外的钉扎效应。这种相互作用与其他复杂的磁耦合相互竞争，导致在磁化翻转过程中形成新的畴结构。此时的交换偏置场和矫顽力场强烈的依赖于磁化翻转过程，二者都极大地增加。不平滑的磁滞回线表明界面处未钉扎磁矩的存在，这些未钉扎的磁矩主宰了小磁场下的磁化翻转过程。在Fe4N（4 nm）薄膜中，磁矩排列是无序的，各种磁结构相互竞争导致无序的磁化翻转过程［31，32］。

图41.Fe4N（4 nm）/CoN（8 nm）双层膜在50 kOe的场冷之后测得的不同温度下的磁滞回线，（a）3、（b）10、（c）50、（d）100 K［31，32］

为了得到清晰直观的物理图像来明确这些现象的产生机制，界面自旋结构的排列呈现在图42中［31，32］。如图42（a）所示，当温度低于交换偏置符号的转变温度时，界面交换作用主要是在界面处Fe和Co磁矩的铁磁耦合，这样磁滞回线就朝着负场方向偏移。转变温度附近，界面处的铁磁耦合和反铁磁耦合共存，磁矩的倾斜是由于反铁磁晶粒的不稳定性和阻挫效应导致。高于转变温度，反铁磁耦合占主导。界面处Fe和Co的磁矩本征的反铁磁耦合可能导致了高于奈尔温度的交换偏置的存在。对于不平滑的磁滞回线的解释，界面自旋排列如图43（b）所示。畴与畴的相互作用使部分铁磁磁矩倾斜，磁化翻转不完全被钉扎效应所控制，在低场范围内，磁矩发生倾斜引起磁化强度的增强。而在零场附近磁化强度的快速下降则是快速翻转的界面磁矩所导致。磁矩的倾斜在不平滑的磁滞回线中起主要作用［31，32］。

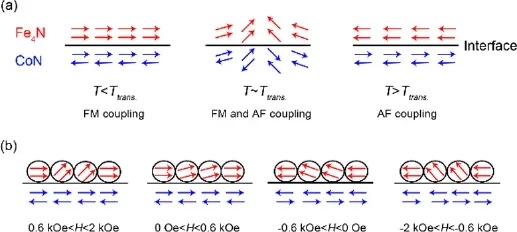
图42.（a）交换偏置符号随温度发生转变的原理图，（b）Fe4N（4 nm）/CoN（8 nm）双层膜复杂的磁化行为的原理图［31，32］

C.外延Fe4N/CoN双层膜的电输运特性

Fe4N/CoN双层膜的AMR采用PPMS来测量。外加磁场平行于薄膜表面，样品在50 kOe的磁场下冷却到3 K。在3 K下，加不同的磁场从0.5到50 kOe测AMR。在其它温度下，加50 kOe的磁场测AMR曲线。磁场从0◦顺时针旋转到360◦，再从360◦逆时针旋转到0◦［30，45］。图44为冷却场HFC、外加磁场Hex、磁化强度M以及电流方向I的示意图。

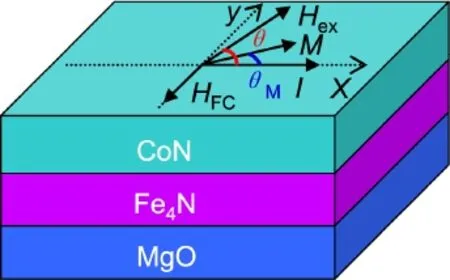
图43.冷却场HFC、外加磁场Hex、磁化强度M以及电流方向I的示意图［30，45］

图44（a）∼（e）为不同Fe4N厚度的Fe4N/CoN（8 nm）双层膜在3 K下的磁滞回线［30，45］。我们可以观察到磁滞回线的偏移明显，说明存在交换偏置。随着厚度的减小，交换偏置增加。对于Fe4N（6 nm）/CoN（8 nm）样品，交换偏置有最大值为410 Oe，并且伴有矫顽力的极大增加。磁滞回线的形状也与其他样品不同，1 kOe的磁场不足以达到Fe4N的饱和磁化强度。这说明在Fe4N（6 nm）/CoN（8 nm）样品中产生了最强的界面交换耦合。通过AMR测量，我们得到了进一步的证据。图44（f）∼（j）为不同Fe4N厚度的Fe4N/CoN（8 nm）双层膜在3 K下的AMR曲线［30，45］，实线为拟合曲线。场冷却过程和交换偏置的测量相同，外加磁场为0.5 kOe。我们首先注意到在交换偏置最明显的Fe4N（6 nm）/CoN（8 nm）样品中，AMR曲线仅仅有一个最小值出现在250◦，打破了cos2θ依赖关系和二重对称性。这表明磁矩被钉扎在交换偏置方向，因为0.5 kOe的磁场不足以打破铁磁/反铁磁耦合。在Fe4N（8 nm）/CoN（8 nm）样品中，AMR曲线可以很好的符合cos2θ函数关系。但是，由于磁化强度滞后于外加的小磁场，使得明显的磁滞出现。相位的滞后证实CoN对Fe4N的钉扎作用。随着Fe4N厚度的增加，相位延迟一直存在。我们还观察到所有的AMR值都是负的，这与单层Fe4N的AMR结果一致。随着Fe4N厚度的增加，AMR值减小。负的AMR说明在Fe4N薄膜中少数自旋电子导电是主要的［46，47］。因为在费米面处自旋向下的电子态密度要大于自旋向上电子。这是Fe4N薄膜中负的自旋极化率，负的AMR的根源［30，45］。

还有一个显著的现象就是随着Fe4N厚度的增加，AMR曲线逐渐从余弦曲线转变成类似矩形状曲线，尤其是在Fe4N（20 nm）/CoN（8 nm）样品中。在界面处，Fe4N的磁矩旋转由界面的磁相互作用所主宰。为证实界面效应，我们首先需要排除单层Fe4N和CoN薄膜的AMR影响［30，45］。如图45（a）所示，单层Fe4N薄膜的AMR表现出二重对称性，是很好的余弦曲线。另外，我们还研究了不同厚度、取向、基底等对Fe4N薄膜的AMR效应的影响，并没有发现这种矩形状的AMR曲线。而CoN的AMR曲线为一条直线，如图45（b）所示，因此我们可以得出矩形状的AMR应当是来源于界面效应。随着Fe4N厚度的增加，钉扎效应减弱。因此在界面处Fe4N磁矩的有序排布减弱。这一减弱的有序性使得界面自旋散射增加。界面自旋散射引入了额外的各向异性。根据傅里叶变换可知，矩形波可以分解为多个余弦波。因此，多个余弦函数的叠加导致了矩形状AMR的出现［30，45］。

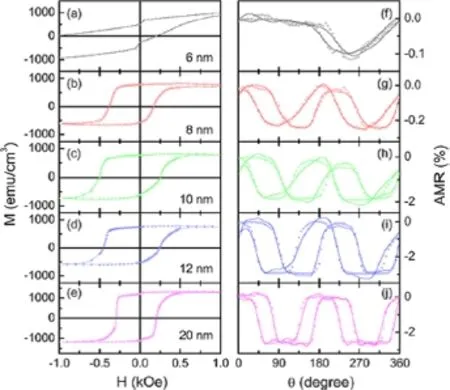
图44.Fe4N/CoN（8 nm）双层膜在3 K下的磁滞回线（左）和AMR曲线（右），（a）（f）6、（b）（g）8、（c）（h）10、（d）（i）12、（e）（j）20 nm［30，45］

为了证实这一猜想，我们尝试采用傅里叶变换公式来拟合AMR曲线。最终，运用下面这一公式能够很好的拟合AMR曲线，

其中，C0为常数，C1、C2、C4、C6、C8以及C10分别为cosθ、cos2θ、cos4θ、cos6θ、cos8θ和cos10θ项的傅里叶系数。拟合的傅里叶系数见表I［30，45］。

一般来说，铁磁体中AMR曲线是二重对称的，仅仅依赖于cos2θ。可是，cos4θ出现在单层Fe4N的AMR中，这是由于Fe4N薄膜的四方畸变诱导了晶体场劈裂。在低温下，单层Fe4N的AMR不仅仅包含cos2θ，还包含cos4θ。cos2θ和cos4θ的傅里叶系数C2和C4强烈地依赖于温度。随着温度的增加，C4快速消失。低温下C4的出现是由于晶格结构的变化导致晶体场的劈裂。低温下的晶格收缩引起四方晶格畸变［30，45］。其他系数的物理含义可以通过比较来解释。首先，在Fe4N厚度为6 nm的样品中，C1不能被忽略，否则曲线不能被拟合。从表1中可以看出，6 nm样品所有的傅里叶系数中，C1的贡献最大，甚至超过C2。6 nm样品的交换偏置也是最大的，因此C1可能是来自于交换偏置导致的大的单向各向异性。随着Fe4N厚度的增加，C1的贡献减小。这一变化趋势和交换偏置的变化趋势相一致，这说明cosθ项是交换偏置的贡献。Cui等报道交换偏置对磁化强度的重新排布有着非常重要的影响。当交换偏置的大小和外加磁场相比拟时，AMR展现360◦为一个周期的cosθ依赖关系。交换偏置场与外加磁场的矢量和决定了磁化强度的方向，因此对称性也被打破。这一观点证实了我们的猜想，交换偏置的单向各向异性诱导cosθ依赖关系［30，45］。

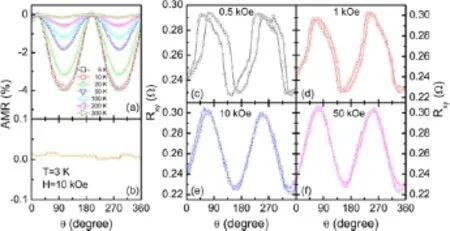
图45.（a）单层Fe4N薄膜的AMR曲线，（b）单层CoN薄膜的AMR曲线，（c）-（f）Fe4N/CoN双层膜在3 K下测得的平面霍尔效应［30，45］

随着铁磁层厚度的增加，矩形状的AMR更加明显。根据傅里叶变换，仅仅用C1、C2、C4这三项的叠加是无法得到矩形状的AMR，高阶项将会起到非常重要的作用。已经有很多报道显示交换耦合除了会导致单向各向异性之外，还会诱导高阶各向异性，包括二重各向异性、四重各向异性，甚至三重和六重各向异性［48］。从表I.中可以看到，随着Fe4N厚度的增加，高阶项的比例在增大。厚度为12和20 nm时，C6超过C1，排在第二位。同时，C8和C10的贡献也逐渐增加。相比较而言，C6的增加是最明显的，其次是C10，C8最弱。我们由此分析，随着厚度的增大，C1的贡献减弱，而高阶项的贡献增强。C1的减弱暗示交换偏置的减弱。这两个相反的变化说明高阶项的产生是来自于减弱的交换偏置。减弱的钉扎效应使得界面处磁矩排布轻微地无序，导致界面自旋散射增强。高阶项的产生应当是界面自旋散射的结果［30，45］。

表I.通过拟合公式（7）得到的傅里叶系数

为了明确不寻常的AMR的根源，我们还测量了平面霍尔效应（PHE）。平面霍尔效应也是测量交换偏置系统中的交换各向异性的有效方法［49］。测量过程与测量AMR相同，结果如图45（c∼f）所示［30，45］。在0.5 kOe的磁场下，相位滞后出现，表明交换偏置的存在。说明交换偏置也能通过PHE测量反映出来。随着磁场的增加，相位滞后消失。但是在PHE测量中并没有观察到矩形状，这一点不同于AMR。AMR和PHE的传统解释是随着外加磁场和电流方向的夹角变化，散射几率会发生变化。考虑到立方对称性导致矩阵元的消失以及Onsager公式，面内纵向电阻率ρxx（AMR）和横向电阻率ρxy（PHE）的表达式为［50］

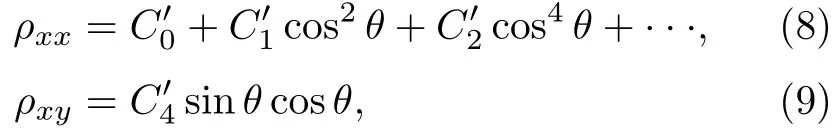
很明显，AMR包括二重对称和四重对称项，甚至高阶对称项，而PHE仅仅包含二重对称项。因此在AMR中观察到对称性的变化，而PHE中没有。我们运用这一解释来分析我们的实验结果。通过比较，我们发现AMR和PHE中都观察到了磁滞现象。同时，交换偏置打破了Fe4N的对称性，诱导AMR中的高阶项产生，因此矩形状AMR出现。而PHE仅仅依赖于二重对称性，所以没有矩形状出现［30，45］。

现在我们尝试着给出高阶项的物理含义。通常情况下，高阶项相比于C2非常小，可以忽略。可是，在Fe4N/CoN双层膜中，二重对称性打破，AMR变为矩形状，因此我们不得不重新考虑它。有三个因素对于矩形状的AMR出现是关键的：（1）交换偏置诱导的单向各向异性产生cosθ项；（2）Fe4N中本征的二重和四重对称性是AMR的主体部分；（3）界面自旋散射引入额外的各向异性，这是高阶项产生的关键。随着Fe4N厚度的增加，交换偏置减小，cosθ项的贡献减小，Fe4N本征的AMR贡献仍是主体，而界面自旋散射的贡献增加。三个因素随着厚度的变化此消彼长，最终导致了矩形状AMR的产生［30，45］。

为了进一步理解矩形状AMR，我们测量了不同外加磁场下的AMR曲线。如图46，当外加磁场增加时，相位滞后逐渐减小。大的外加磁场导致磁化强度与外加磁场同步旋转。因此，磁场高于5 kOe时，相位滞后消失。可是，AMR曲线仍然保持矩形状，独立于外加磁场。矩形状AMR的存在表明Fe4N的磁化强度的旋转被反铁磁的CoN所影响。Fe4N/CoN双层膜的界面耦合是矩形状AMR产生的关键因素。尽管外加磁场足够大能够饱和Fe4N的磁化强度，但是3 K下的交换耦合仍然存在。磁耦合相互作用导致界面自旋散射的产生。矩形AMR应该是界面磁耦合和自旋轨道耦合的叠加［30，45］。

图487给出了Fe4N（20 nm）/CoN（8 nm）双层膜不同温度下的AMR曲线［30，45］。在50 kOe的磁场下，没有相位滞后出现。仅仅在低温下出现矩形状AMR。在20 K下，矩形状AMR完全转变为余弦曲线。矩形状AMR的消失表明由于增强的热扰动导致交换相互作用的减小，这暗示矩形状AMR确实依赖于界面交换耦合。图48给出了Fe4N（20 nm）/CoN（8 nm）双层膜的AMR比值随磁场和温度的变化曲线［30，45］。图48a）中，随着磁场的增加，AMR的绝对值增加。Fe4N的磁矩沿着外加磁场的一致排列使得界面钉扎磁矩的旋转角度增大。因此，散射效应更显著，导致AMR绝对值增加。图48b）中，随着温度的增加，AMR的绝对值快速减小，这是由于温度的升高引入了声子散射，导致AMR绝对值的减小。

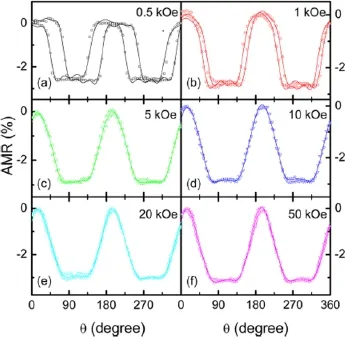
图46.Fe4N（20 nm）/CoN（8 nm）双层膜在3 K下不同磁场测量的AMR曲线［30，45］

图47.Fe4N（20 nm）/CoN（8 nm）双层膜在50 kOe下不同温度测量的AMR曲线［30，45］

VI.Fe4N/ALQ3/Co自旋阀的结构与物性

本节我们将重点介绍Fe4N/Alq3/Co有机自旋阀的表面形貌、晶体结构、磁性质、电输运特性和磁电阻效应［30，51］。

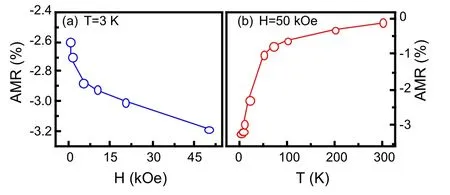
图48.（a）Fe4N（20 nm）/CoN（8 nm）双层膜在3 K下AMR比值随磁场的变化，（b）Fe4N（20 nm）/CoN（8 nm）双层膜在50 kOe下AMR比值随温度的变化［30，45］

A.Fe4N/Alq3/Co的结构

图49出了Fe4N/Alq3/Co有机自旋阀的TEM图像，从图50（a）中的低分辨形貌中可以证实各层膜的厚度［30，51］。Fe4N为10 nm，Alq3为20 nm，Co为20 nm，Cu为30 nm。图49（b）为Fe4N/Alq3界面的形貌，界面非常尖锐。外延的Fe4N和非晶的Alq3形成鲜明的对比。清晰的Fe4N/Alq3界面表明二者的扩散较弱。由于LaAlO3（100）基底和Fe4N的晶格相匹配，使得生长在其上的Fe4N表面较为平坦，这种平坦且坚硬的合金表面有利于Alq3这种柔性有机材料的生长，极大地抑制了界面互扩散，更容易形成尖锐的界面［30，51］。图49（b）的插图为选区电子衍射图，清晰的排布有序的点阵表明了Fe4N的外延生长。图49（c）为Alq3/Co的形貌，界面处存在较弱的互扩散。一方面，高质量的Fe4N/Alq3界面是形成较好的上层界面的基石。另一方面，对靶溅射的优势能够抑制Alq3和Co的相互扩散［52，53］。因为在沉积Co的过程中，Alq3层将免受Co的高能粒子的轰击。大面积的均匀性、较低的基底温度以及相对惰性的化学结合能够减小Co与Alq3的相互混合［30，51］。图49（c）的插图为Fe4N/Alq3/Co有机自旋阀的选区电子衍射图，我们可以观察到多晶的Co和Cu的衍射斑点，还有外延Fe4N的点阵。图50（d）为整个Fe4N/Alq3/Co有机自旋阀的高分辨TEM图像［30，51］。

图50a）为生长在Fe4N表面的Alq3（40 nm）薄膜的原子力显微镜（AFM）图像［30，51］。我们可以看到Alq3薄膜完全覆盖了Fe4N。Alq3的表面粗糙度为3.50 nm，相应的表面起伏显示在图44c）中。Alq3的表面起伏大约在5 nm左右，这意味着在Alq3上沉积Co原子时，Co原子可能会渗透到这5 nm深的孔洞中。这样Co和Alq3的混合就会形成磁性死层。图51（b）为生长在Alq3表面的Co（20 nm）薄膜的AFM图像。Co薄膜的表面比较平滑，表面粗糙度为1.92 nm。

图49.Fe4N/Alq3/Co自旋阀的TEM图［30，51］

图50.（a）Fe4N上的Alq3（40 nm）层的AFM图，（b）Alq3上的Co（20 nm）层的AFM图，（c）和（d）分别为Alq3和Co层的表面起伏［30，51］

图51（d）为相应的Co薄膜的表面起伏。Co薄膜的表面起伏小于5 nm，说明Co和Alq3的相互扩散较弱。同时也说明Alq3/Co界面的形貌取决于Alq3薄膜［30，51］。

B.Fe4N/Alq3/Co的输运特性和磁性

图51为Fe4N/Alq3/Co有机自旋阀的结构示意图以及电输运测量的接线图［30，51］。Fe4N/Alq3/Co有机自旋阀的磁电阻测量是从3 K到300 K，外加磁场平行于样品表面，磁场扫描范围为±1 kOe，所加电流恒定为0.1 mA。测量的样品为Fe4N/Alq3（t）/Co有机自旋阀，t=5、40、80、120、260 nm。图52为80 nm样品在不同温度下的磁电阻随磁场的变化曲线。可以看到典型的双峰磁电阻曲线，但是磁电阻的值较小。在只有一个单晶铁磁电极的类似于自旋阀的结构中也能观察到相似的双峰信号［54-56］。这种磁电阻称为隧穿各向异性磁电阻（TAMR），根源于外延铁磁电极的磁晶各向异性。我们需要去辨别这种TAMR效应和正常的自旋阀效应。在外延Fe4N薄膜中，磁电阻以及各向异性磁电阻在之前的工作中已经做了详细的描述，外延Fe4N中的磁电阻曲线只有一个峰值。而且，在5 K下的各向异性磁电阻值可以达到-3.6%，远大于我们从有机自旋阀中测量的磁电阻。无论是磁电阻曲线的形状还是大小，都不同于TAMR。所以TAMR被排除，这种双峰磁电阻是来源于有机自旋阀的自旋相关的输运。双峰暗示电阻的变化依赖于两个铁磁电极Fe4N和Co的磁矩排布。磁电阻定义为MR=（RAP-RP）/RAP，RAP和RP分别为Fe4N和Co的磁矩反平行和平行时的电阻。从图52a）中可以看到平行组态和反平行组态。很明显，RP要大于RAP，磁电阻为负值，这与LSMO/Alq3/Co自旋阀的结果一致［57］。在LSMO/Alq3/Co自旋阀中，Xiong等人［57］认为Co的自旋极化率为负值。而Santos等人［58］观察到在Alq3/Co界面处Co的自旋极化率为正值。因此，负的磁电阻是由于LSMO/Alq3/Co自旋阀中Co和LSMO相反的自旋极化率所导致。根据磁电阻公式［30，51］

其中，PFe4N和PCo分别为Fe4N和Co的自旋极化率。t0为磁性死层的厚度，λs为自旋扩散长度。如果Co和Fe4N的自旋极化率如理论预测的那样都为负值的话，就会得到正的磁电阻。可是，我们在Fe4N/Alq3/Co中得到的是负磁电阻。根据Fe4N基隧道结的结果可知Fe4N的自旋极化率为负值，那么Alq3/Co界面的自旋极化率就为正值，和Santos等人实验测得的结果一致。两个铁磁层/有机层界面相反的自旋极化率最终导致了负磁电阻［30，51］。

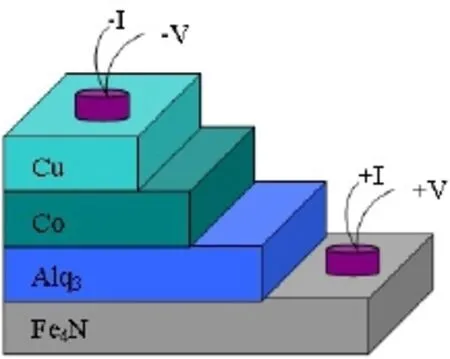
图51.Fe4N/Alq3/Co自旋阀的示意图［30，51］

图52.Fe4N/Alq3（80 nm）/Co有机自旋阀在不同温度下的磁电阻曲线［30，51］

关于有机自旋阀的负磁电阻有一个理论模型，即在LSMO和Co的费米面之上存在一条很窄的导电通道［59］。LSMO中自旋向上的电子注入到这一导电通道中，然后通过跳跃导电进入到Alq3层中，当它们到达Co电极时，电子被注入到Co的自旋向下态。在Fe4N/Alq3/Co有机自旋阀中，对于平行组态，来自Fe4N的自旋向下电子注入到Fe4N/Alq3界面，然后通过Alq3/Co界面进入到Co的自旋向上态而产生一个高电阻；对于反平行态，Fe4N的自旋向下电子注入到Co的自旋向下态而形成低电阻［30，51］。

自旋杂化诱导的极化态（Spin-hybridizationinduced polarized states，SHIPS）理论也证明了我们的解释［60］。SHIPS理论指出自旋相关的铁磁层/有机层界面的杂化对有效自旋极化率的影响将会引起注入自旋的符号反转。杂化可能会有利于电极的自旋相关的态密度。有效自旋极化率相关的类似Julliere公式定义为［58］

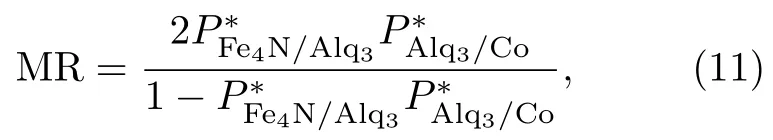
在不同温度下，所有的磁电阻展现双峰曲线和负磁电阻。在3 K下，反平行组态呈现明显的不对称，两个反平行组态的电阻差异明显。随着温度的升高，不对称消失，磁电阻也逐渐减小。随着温度的升高，磁电阻的值逐渐减小。在室温下，磁电阻变为0［30，51］。有两个因素影响磁电阻随温度的减小。一个为铁磁电极的自旋极化率的减小，另一个为Alq3层中自旋扩散长度的减小。Xiong等人［57］认为由于Alq3层自旋弛豫时间的增加导致自旋扩散长度λs的减小，最终导致磁电阻消失。而Wang等人［56］认为LSMO的自旋极化率的减小是磁电阻消失的关键，Alq3层较弱的自旋轨道耦合使得自旋扩散长度并不强烈地依赖于温度。LSMO较低的居里温度导致自旋极化率减小。可是用高居里温度的Fe替代LSMO，并没有改善室温磁电阻［61］。尽管Fe4N和Co的居里温度远高于室温，磁电阻在室温下仍然消失。有机自旋阀中磁电阻的根源是自旋相关的载流子注入。温度升高不可避免的会导致自旋无序和自旋翻转散射的增加［62］。因此磁电阻的减小可以归结为［30，51］铁磁层/有机层界面的自旋波动和减小的界面自旋极化率。

为了证实磁电阻与两个铁磁层的磁化方向的排布有关，我们测了Fe4N/Alq3/Co有机自旋阀的磁滞回线。图53（a）和（b）给出了80 nm样品在70 K下的磁电阻曲线和磁滞回线。磁滞回线出现两个台阶，这是由于Fe4N和Co的矫顽力不同导致的。这意味着Alq3将两个铁磁层很好的分隔开。我们观察到磁化翻转与磁电阻的高低组态变化相吻合。因此，我们观察到的磁电阻现象毫无疑问是有机自旋阀的自旋相关效应。当外加磁场在Fe4N和Co的矫顽力之间时，两个电极的磁化方向反平行，而当磁场大于它们的矫顽力时，磁化方向平行排列。图54（c）和（d）给出了120 nm样品在70 K下的磁电阻曲线和磁滞回线。我们可以看到磁场在接近±125 Oe时，磁化方向反平行排列，低电阻态出现［30，51］。

图53.Alq3厚度为80 nm和120 nm的样品在70 K下的磁电阻曲线和磁滞回线

图54给出了3 K下不同厚度样品的磁电阻曲线［30，51］。所有的Fe4N/Alq3/Co有机自旋阀都展现了负磁电阻。甚至对于厚度非常薄的5 nm样品，仍然表现出高低组态的变化，说明磁性死层的厚度小于5 nm，这归因于对靶溅射的优势。更重要的是，我们发现除了260 nm样品外，其余样品在反平行组态均表现出明显的不对称。这意味着在两个反平行组态的磁矩排布不同。不同的磁矩排布引起自旋相关散射的改变，因此当扫场过程中，反平行组态的磁电阻不同。这一不对称表明在铁磁层/Alq3界面处磁矩存在交换耦合作用。我们猜想在Fe4N/Alq3/Co有机自旋阀中存在交换偏置，因为不对称发生在低温下的小磁场范围内，在高温下消失，这与交换偏置的特点相同。另外，磁电阻的不对称不依赖于Alq3的厚度。260 nm样品的磁电阻不对称消失可能是由于铁磁层/Alq3界面处弱的交换耦合［30，51］。

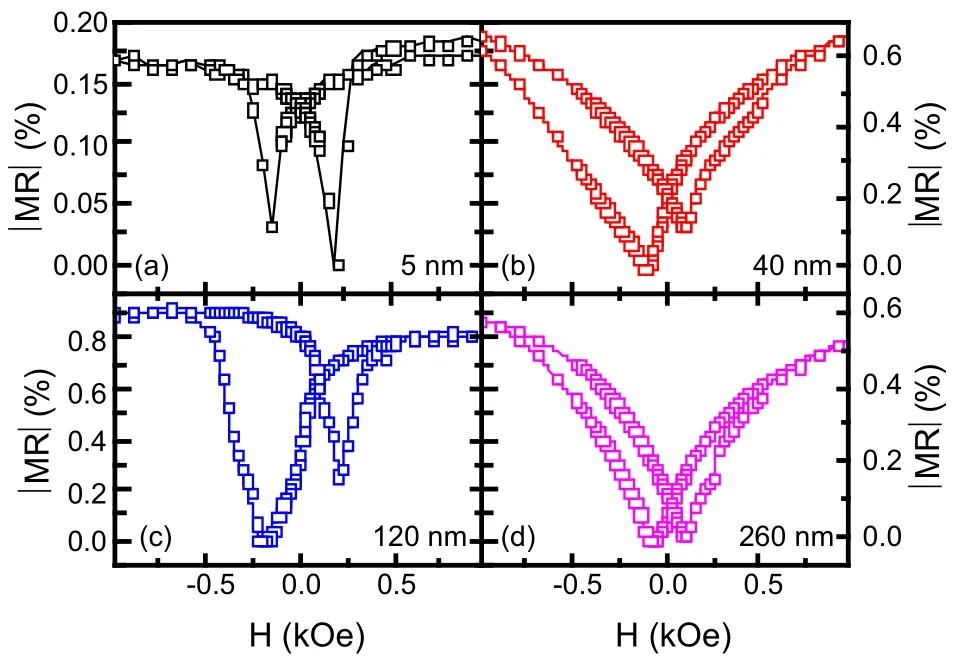
图54.Alq3不同厚度的Fe4N/Alq3/Co有机自旋阀在3 K下的磁电阻曲线［30，51］

为了与磁电阻作比较，图55展现了3 K下不同Alq3厚度的样品的磁滞回线［30，51］。磁滞回线的形状变化对应于磁电阻的变化。我们发现磁滞回线也是不对称的，两个明显的台阶仅仅出现在单支回路上，对应于磁电阻反平行态的不对称。由于在Alq3/Co界面化学相互作用的影响，在Co电极会形成复杂的磁结构。在Alq3/Co界面处Alq3的π分子轨道和Co的d轨道之间进行杂化导致磁硬化效应。发生在Alq3/Co界面的磁硬化效应加强了二者的磁耦合相互作用。部分Co磁矩被钉扎，完全的磁化翻转需要更大的磁场。因此明显的台阶仅仅出现在半支回路上，另外半支回路由于磁矩较容易翻转所以没有展现明显的台阶。在Alq3/Co界面处不可逆的磁化翻转包括自由磁矩和钉扎磁矩的翻转［63］。有两个明显台阶的那支回路刚好对应于反平行态磁电阻较大的那支磁电阻回路，这说明Alq3/Co界面处的交换作用使得部分Co磁矩被钉扎，自旋散射增强，磁电阻增大［30，51］。

图55.Alq3不同厚度的Fe4N/Alq3/Co有机自旋阀在3 K下的磁滞回线［30，51］

为了证实我们的想法，测量了Fe4N/Alq3/Co有机自旋阀的交换偏置。外加磁场平行于样品表面，样品在±50 kOe的冷场下被冷却到3 K。从3到300 K测量了不同温度下的磁滞回线。图56给出了5 nm样品在±50 kOe的磁场下冷却到3 K测得的磁滞回线［30，51］。当冷却磁场的方向变化时，磁滞回线的不对称也翻转方向。这证实了钉扎效应的存在。磁滞回线和磁电阻曲线的不对称确实是相关于Alq3/Co界面复杂的磁结构。图57给出了5 nm样品的交换偏置以及矫顽力随温度的变化曲线。3 K下交换偏置为-70 Oe，这是由于Fe4N和Co之间通过5 nm的Alq3层进行强的交换耦合造成的。随着温度的升高，交换偏置和矫顽力均减小，表明热扰动减弱了交换耦合。因此随着温度的升高，磁电阻的不对称性也消失。图58给出了80 nm样品在3 K下面内和面外的磁滞回线。面外磁矩的不饱和表明Fe4N/Alq3/Co有机自旋阀没有垂直各向异性，所有磁矩沿面内排布［30，51］。

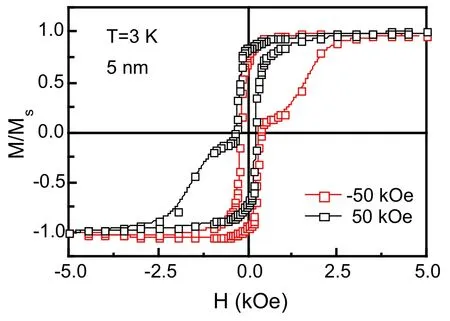
图56.Fe4N/Alq3（5 nm）/Co有机自旋阀在3 K下的磁滞回线［30，51］

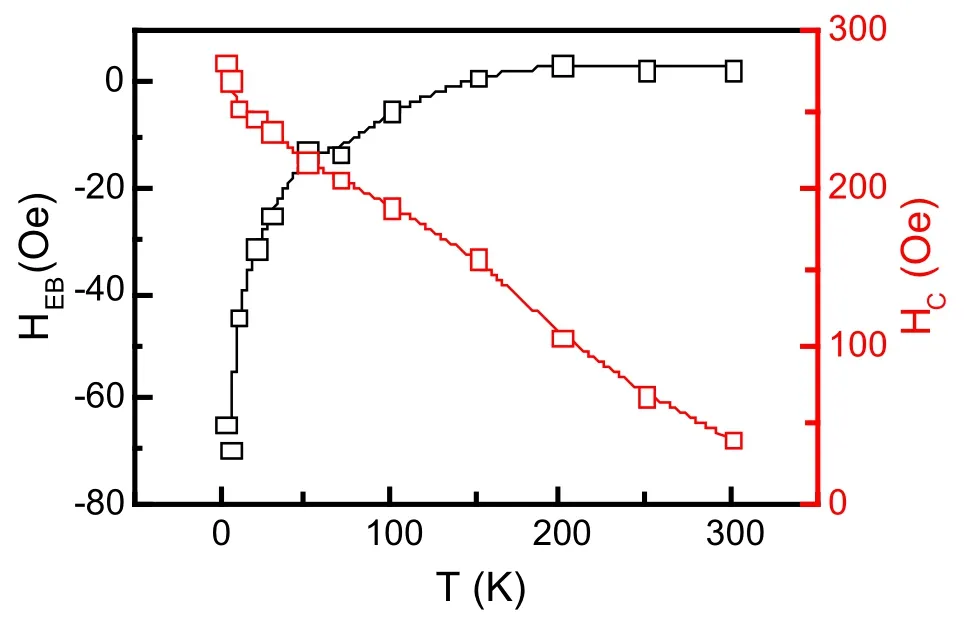
图57.Fe4N/Alq3（5 nm）/Co有机自旋阀的交换偏置场和矫顽力场随温度的变化曲线［30，51］

图58.Fe4N/Alq3（80 nm）/Co有机自旋阀在3 K下磁场平行和垂直于膜面的磁滞回线［30，51］

VII.Fe4N基隧道结的结构与物性

Komasaki等人［64］在热氧化硅基底上制得的Fe4N/MgO/CoFeB隧道结上测得的TMR值为-75%，Fe4N由于铜衬层的存在而表现出很好的外延生长。Sunaga等人［65］制备了Fe4N/MgO/CoFeB与Fe/MgO/CoFeB隧道结，二者做比较，如图59所示，Fe/MgO/CoFeB隧道结的平行态电导基本不随偏压变化，TMR值随偏压的变化来源于反平行态的电导。而Fe4N/MgO/CoFeB隧道结中，平行态与反平行态电导都随偏压变化，使得TMR值随偏压的变化曲线与之基本相同，且呈现负值。Narahara等人［66］用分子束外延法在M-gO（001）基底上制备了Fe4N/MgO/Fe隧道结，并且给出了M-H曲线。由于两个铁磁电极的矫顽力不同，在磁化过程中磁矩翻转的不同步导致测得的磁滞回线呈现阶梯状。

Fe4N负的自旋极化率不仅造成了负的隧穿磁电阻，而且电流诱导的磁化翻转也会有很大的不同。根据自旋角动量转移理论，作用在自由层上的自旋矩可以写为［67］

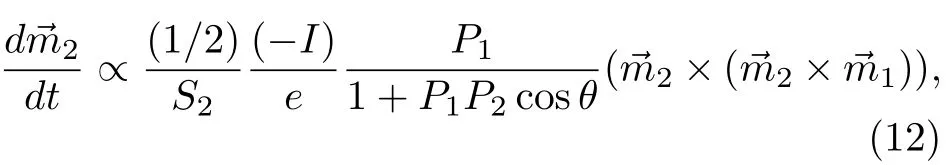
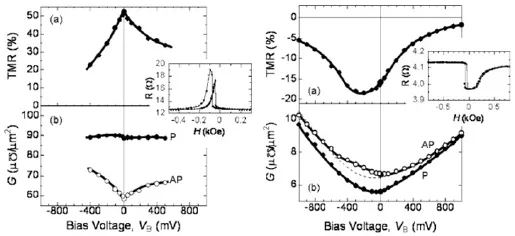
图59.Fe-MTJ（左）和Fe4N-MTJ（右）的TMR以及电导随偏压的变化关系

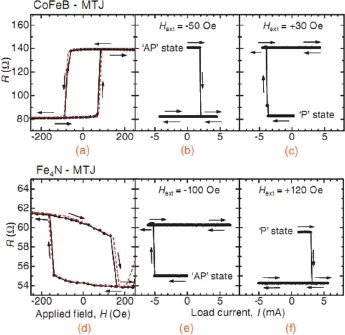
图60.CoFeB-MTJ和Fe4N-MTJ的R-H、R-I曲线

Isogami等人［67］研究了CoFeB/MgO/Fe4N隧道结，发现电流诱导的磁化翻转确实出现了与CoFeB/MgO/CoFeB磁性隧道结相反的现象，如图60所示，相同的外加磁场下，CoFeB-MTJ从低阻态转向高阻态，而Fe4N-MTJ从高阻态转向低阻态。相同的负载电流下，电阻随电流的变化也正好相反。Borsa等人［68］研究Cu3N薄膜生长在MgO基底和MgO基底上有Fe4N缓冲层的性质时提出由于Fe4N是铁磁性导体，而Cu3N是低能带隙（1.65 eV）的绝缘体，两者为制备低电阻的磁性隧道结提供了条件。Narahara等人［69］提出基于氮化物的以Fe4N为铁磁电极之一的磁性隧道结Fe3N/AlN/Fe4N。主要介绍了如何在Si（111）基底上制备磁性隧道结Fe3N/AlN/Fe4N并给以证明，在280 K下测量了磁性隧道结的磁滞回线。各层厚度为Fe3N（30 nm）/AlN（2 nm）/Fe4N（25 nm）。其中顶层Fe3N的矫顽力为160 Oe，饱和磁化强度为800 emu/cm3。底层Fe4N的矫顽力为50 Oe，饱和磁化强度为1600 emu/cm3，这与在块体中得到的数值相一致。Navio等人［70］提出了以Fe4N为铁磁性电极，金属铜为中间层的自旋阀结构，即Fe4N/Cu/Fe4N。应用半导体Cu3N和顺磁性的FeN的热稳定性，通过比较缓和的700 K退火使全氮的三层膜FeN/Cu3N/Fe4N部分转变成自旋阀结构Fe4N/Cu/Fe4N。退火温度之所以选择700 K，是因为Cu3N薄膜完全分解成金属铜薄膜的温度和无磁性的FeN转化成铁磁性的Fe4N相的退火温度都为700 K。

VIII.结论与展望

自从理论预测Fe4N具有高的自旋极化率，近年来Fe4N又受到了人们的关注。人们分别研究了Fe4N单层膜、双层膜、自旋阀以及隧道结的结构、磁性和电输运特性，为其在自旋电子学器件上的应用提供了实验基础。但是对于Fe4N的反常霍耳效应、Fe4N/半导体异质结构的电输运特性、Fe4N薄膜的磁畴结构及其翻转动力学、Fe4N/多铁异质结构的界面耦合、Fe4N/有机分子界面的自旋翻转等仍问题需要进一步深入研究。这些问题的研究将使人们更加清楚地了解Fe4N薄膜及其异质结构的微观结构和物性变化规律，推动Fe4N薄膜材料在自旋电子学器件上的应用。

在完成本文的过程中，主要参考了作者指导的硕士生封秀平和李滋润同学的学位论文。

本文的工作得到了得到国家自然科学基金（51171126）、天津市自然科学基金重点项目（12JCZDJC27100）和教育部新世纪优秀人才支持计划（NCET-13-0409）的资助。

参考文献

［1］Baibich M N，Broto J M，Fert A，Van Dau F N，Petroff F，Etienne P，Creuzet G，Friederich A，C-hazelas J.Phys.Rev.Lett.，1988，61（21）：2472-2475

［3］Inoue J and Maekawa S.Phys.Rev.B，1996，53（18）：R11927

［4］Slonczewski J C.Phys.Rev.B，1989，39：6995

［5］Haghiri-Gosnet A M，Arnal T，Soulimane R，Koubaa M，Renard J P.phys.stat.sol.（a），2004，201（7）：1392-1397

［6］Wang F J，Vardeny Z V.J.Mater.Chem.，2009，19：1685

［7］Groot R A，Mueller F M，Buschow K H J.Phys. Rev.Lett.，1983，50：2024

［8］Yanase Y，Siratori K.J.Phy.Soc.Japn.，1984，53：312

［9］Zhang Z，Satpathy S.Phys.Rev.B，1991，44：13319

［10］Kokado S，Fujima N，Harigaya K，Shimizu H，Sakuma A.Phys.Rev.B，2006，73：172410

［11］Gallego J M，Grachev S，Borsa D M，Boerma D O，Ecija D，Miranda R.Phys.Rev.B，2004，70（11）：115417/1-11

［12］Navio C，Alvarez J，Capitan M J，Ecija D，Gallego J M，Yndurain F，Miranda R.Phys.Rev.B，2007，75（12）：.125422/1-7

［13］Grachev S Y，Borsa D M，Boerma D O.Surf.Sci.，2002，515（2-3）：359-368

［15］Frazer B C.Phys.Rev.，1958，112（3）：751-754

［16］Houari A，Matar S F.J.Magn.Magn.Mater.，2010，322（6）：658-660

［17］Ito K，Lee H，Harada K，Suzuno M，Suemasu T，Takeda Y，Saitoh Y，Ye M，Kimura A，Akinaga H. Appl.Phys.Lett.，2011，98（10）：102507/1-3

［18］Grachev S，Borsa D M，Vongtragool S，Boerma D O.Surf.Sci.，2001，482-485：802-808

［19］Wang L L，Wang X，Ma N，Zheng W T，Guan Q F，Zhao J，Chen Y，Feng S H.Mater.Chem.Phys.，2006，100（2-3）：304-307

［20］Arabczyk W，Zamlynny J，Moszyski D.Pol.J. Chem.Technol.，2010，12（1）：38-43

［21］Kim T K，Takahashi M.Appl.Phys.Lett.，1972，20（12）：493-494

［22］Wriedt H A，Gokcen N A，Nafziger R H.Bull.Alloy Pha.Diag.，1987，8（4）：355-357

［23］Mi W B，Guo Z B，Feng X P，Bai H L.Acta Mater.，2013，61（17）：6387-6395

［24］封秀平，γ′-Fe4N薄膜的结构、磁性和磁电阻效应：［硕士学位论文］，天津：天津大学，2011

［25］Mi W B，Feng X P，Duan X F，Yang H，Li Y，Bai H L.Thin Solid Films，2012，520：7035-7040

［26］姜寿亭，李卫，凝聚态磁性物理，北京：科学出版社，2003

［27］Chattopadhyay S K，Meikap A K，Lal K，Biswas D，Chatterjee S K，Ghosh M，Baba K，Hatada R.Solid State Commun.，1998，108（12）：977-982

［28］Mcguire T R，Potter R I.IEEE T.Magn.，1975，11（4）：1018-1038

［29］Li Z R，Feng X P，Wang X C，Mi W B.Mater.Res. Bull.2015，65：175-182

［30］李滋润，Fe4N基双层膜和有机自旋阀的结构、磁性和磁电阻效应：［硕士学位论文］，天津：天津大学，2015

［31］Li Z R，Mi W B，Wang X C，Bai H L.J.Magn. Magn.Mater.，2015，379：124-130

［32］Lamirand A D，Soares M M，Ramos A Y，Tolentino H C N，Santis M D，Cezar J C，De Siervo A，Jamet M.Phys.Rev.B，2013，88（14）：140401（R）/1-5

［33］Mittendorfer F，Weinert M，Podloucky R，Redinger J.Phys.Rev.Lett.，2012，109（01）：015501/1-5

［34］Mi W B，Feng X P，Bai H L.J.Magn.Magn.Mater.，2011，323（14）：1909-1913

［36］Leighton C，Fitzsimmons M R，Yashar P，Hoffmann A，Nogus J，Dura J，Majkrzak C F，Schuller I K. Phys.Rev.Lett.，2001，86（19）：4394-4397

［38］Rana R，Pandey P，Rana D S.Appl.Phys.Lett.，2014，104（09）：092413/1-5

［40］Ali M，Adie P，Marrows C H，Greig D，Hickey B J，Stamps R L.Nat.Mater.，2007，6：70-75

［41］Gredig T，Krivorotov I N，Eames P，Dahlberg E D. Appl.Phys.Lett.，2002，81（7）：1270-1272

［42］Radu F，Etzkorn M，Siebrecht R，Schmitte T，West-erholt K，Zabel H.Phys.Rev.B，2003，67（13）：134409/1-11

［43］Lamirand A D，Soares M M，Ramos A Y，Tolentino H C N，Santis M D，Cezar J C，De Siervo A，Jamet M.Phys.Rev.B，2013，88（14）：140401（R）/1-5

［44］ZhangS，LiZ.Phys.Rev.B，2001，65（05）：054406/1-4

［45］Li Z R，Mi W B，Wang X C，Zhang X X.ACS Appl. Mater.&Interfaces，2015，7（6）：3840-3845

［46］Tsunoda M，Komasaki Y，Kokado S，Isogami S，Chen C C，Takahashi M.Appl.Phys.Express，2009，2（08）：083001/1-3

［47］Tsunoda M，Takahashi H，Kokado S，Komasaki Y，Sakuma A，Takahashi M.Appl.Phys.Express，2010，3（11）：113003/1-3

［48］Kim J V，Stamps R L，McGrath B V，Camley R E. Phys.Rev.B，2000，61（13）：8888-8894

［49］Lu Z Q，Pan G，Lai W Y.J.Appl.Phys.，2001，90（3）：1414-1418

［50］Hu C R，Zhu J，Chen G，Li J X，Wu Y Z.Phys.Lett. A，2012，376（45）：3317-3321

［51］Li Z R，Wang X C，Dai H T，Mi W B，Bai H L.Thin Solid Films（2015）In Press

［52］Lin C，Sun D C，Ming S L，Jiang E Y，Liu Y G. Thin Solid Films，1996，279（1-2）：49-52

［53］Noda K，Hirata T，Kawanabe T，Naoe M.Vaccum，1998，51（4）：687-690

［56］Wang K，Sanderink J G M，Bolhuis T，Van Der W W G，De Jong M P.Phys.Rev.B，2014，89（17）：174419/1-8

［57］Xiong Z H，Wu D，Vardeny Z V，Shi J.Nature，2004，427：821-824

［58］SantosTS.Phys.Rev.Lett.，2007，98（01）：016601/1-4

［59］Dediu V，Hueso L E，Bergenti I，Riminucci A，Borgatti F，Graziosi P，Newby，casoli F，De Jong M P，Taliani C，Zhan Y.Phys.Rev.B，2008，78（11）：115203/1-6

［60］Barraud C，Seneor P，Mattana R，Fusil S，Bouzehouane K，Deranlot C，Graziosi P，Hueso L，Bergenti I，Dediu V，Petroff F，Fert A.Nat.Phys.，2010，6：615-620

［61］Wang F J，Xiong Z H，Wu D，Shi J，Vardeny Z V. Synth.Met.，2005，155（1）：172-75

［62］Liu Y，Watson S M，Lee T，Gorham J M，Katz H E，Borchers J A，Fairbrother H D，Reich D H.Phys. Rev.B，2009，79（07）：075312/1-10

［63］Wu R，Wei J Z，Peng X L，Fu J B，Liu S Q，Zhang Y，Xia Y H，Wang C S，Yang Y C，Yang J B.Appl. Phys.Lett.，2014，104（18）：182403/1-4

［64］Komasaki Y，Tsunoda M，Isogami S，Takahashi M. J.Appl.Phys.，2009，105（07）：07C928/1-3

［65］SunagaK，TsunodaM，KomagakiK，Uehara Y，Takahashi M.J.Appl.Phys.，2007，102（01）：013917/1-4

［66］Narahara A，Ito K，Suemasu T.J.Cryst.Growth，2009，311（6）：1616-1619

［67］Isogami S，Tsunoda M，Komasaki Y，Sakuma A，Takahasi M.Appl.Phys.Express，2010，3（10）：103002/1-3

［68］Borsa D M，Grachev S，Presura C，Boerma D O. Appl.Phys.Lett.，2002，80（10）：1823-1825

［69］Narahara and A，Suemasu T.Jpn.J.Appl.Phys.，2007，46（37）：L892-L894

［70］Navio C，Alvarez J，Capitan M J，Camarero J，Miranda R.Appl.Phys.Lett.，2009，94（26）/263112：1-3

A review on the state-of-arts of perovskite Fe4N thin films and heterostructures with promising appolication potentials in advanced spintronics is presented.the brief introduction is followed by a highlight of the crystal structures and physical properties of pervskite Fe4N，and then a comprehensive description on a series of topics on Fe4N，including the preparations of polycrystalline Fe4N thin films，epitaxial Fe4N，Fe4N/CoN bilayers，and Fe4N/Alq3/Co spin-valves on one hand，and on the other hand the characterizations on morphology and microstructures，magnetic properties，exchange bias，spin-dependent electrical transport and magnetoresistance etc，of the tunneling junctions with the Fe4N electrodes.Finally，a short summary with updated perspectives on recent researches on Fe4N is given.

Spintronic Materials:Fe4N Films and Its Heterostructures

Mi Wen-Bo
Department of Applied Physics，Tianjin Key Laboratory of Low Dimensional Materials Physics and Preparation Technology，Tianjin University，Tianjin 300072，China

Spintronics；Fe4N films；Spin vavle；Tunneling junction；Surface morphology；Lattice structure；Magnetic properties；Electronic transport properties；Magnetoresistance

date：2015-05-11

O47

10.13725/j.cnki.pip.2015.04.001

*miwenbo@tju.edu.cn

1000-0542（2015）04-0145-32145

自旋电子学材料：Fe4N薄膜及其异质结构

目录

I.引言

II.Fe4N的晶体结构和基本性质

III.多晶Fe4N薄膜的结构与物性

IV.外延Fe4N薄膜的结构与物性

V.Fe4N/CoN双层膜的结构与物性

VI.Fe4N/ALQ3/Co自旋阀的结构与物性

VII.Fe4N基隧道结的结构与物性

VIII.结论与展望