多维傅里叶变换光谱

赵威，周肇宇，杨金新，戴星灿*

清华大学物理系低维量子物理国家重点实验室，北京100084

多维傅里叶变换光谱

赵威，周肇宇，杨金新，戴星灿*

清华大学物理系低维量子物理国家重点实验室，北京100084

二维或多维傅里叶变换谱的概念最早是在核磁共振（NMR）谱学中提出的，随着激光技术的发展，飞秒脉冲激光的实现使多维傅里叶变换谱的概念被引入到了光学领域，以脉冲激光代替NMR中的射频（RF）场，激光波长从红外延伸到可见光波段。多维傅里叶变换光谱可以同时提供的信息包括量子态上布居数以及量子态间的耦合，所以多维谱可以提供一维谱所无法获取的反映量子系统演化动力学的信息，如量子系统中的能量转移以及分子间的相互作用等。人们使用多维傅里叶变换光谱的方法对碱金属原子、量子阱、分子等量子系统中的动力学过程进行了一系列的研究。

二维傅里叶变换光谱；四波混频；超快激光；锁相

目录

I.引言177

II.四波混频实验方案178

III.锁相的实现179

IV.在简单原子体系中的应用180

V.利用2DFT对量子阱的研究183

VI.其它量子体系中的应用185

VII.总结和展望185

致谢185

186

I.引言

光学多维傅里叶变换（Multidimensional Fouriertransform，MDFT）谱是一种新颖而十分有用的光谱技术，可以用于研究光与物质相互作用的动力学过程以及物质的结构［1］。多维傅里叶变换谱的概念最先在核磁共振谱中提出。在多维傅里叶变换核磁共振谱中，物质处于具有梯度的磁场当中，射频信号脉冲按序列发射而被物质吸收，通过操控与探测射频信号脉冲，经过计算可以得到物质的结构信息。这一技术能够很好的帮助人们了解大分子的物质结构，比如生物大分子与化学聚合物。在过去的十余年中，多维谱的概念被推广到红外和近红外以及可见光波段，人们开始使用足够强度的短脉冲激光代替原有的射频脉冲。在红外波段中，这项技术可以很好地探测分子的振动能级对信号的响应，因此人们可以很好地确定分子的结构与相干动力学过程［2-6］。在使用更高频率的激光脉冲时，我们可以激发与探测分子以及半导体中电子的跃迁过程［7-9］。

使用由多个激发光脉冲组成的序列对物质进行作用，可以得到物质相应的非线性信号，多维傅里叶变换光谱技术可以准确地追踪该非线性信号的相位。在实验中，改变激发光脉冲之间的时间延迟，记录相应的非线性信号光脉冲的相位信息，我们将得到一个基于时域的多维的数据集，对这个数据集做傅里叶变换，最终可以得到多维傅里叶变换光谱。与其它电磁场驱动的光谱技术相比，多维傅里叶变换光谱的优势在于：信号光的相位是被准确探测到的；该技术还可以确定样品能级的极化率；能够描述能级之间的相干耦合；传统光谱学中物质对于光场的非线性响应信号的重叠部分，在多维谱中可以被区分开；信号中物质的非辐射相干贡献可以通过安排合适的激发脉冲时序被分离出来。此外由于多维光谱通常采用飞秒超快激光作为激发光源，同一般的超快泵浦-探测谱一样，多维光谱能够提供被研究体系中的超快动态过程的详细信息。

多维傅里叶变换光谱技术已经有着广泛的应用，仅仅以一篇文章无法完全覆盖这项技术所涉及到的所有内容。二维傅里叶变换光谱技术（2DFT）是目前多维傅里叶变换光谱技术中最为常用的一种。本综述仅以近红外和可见光波段的二维傅里叶变换光谱技术为例，简单地介绍多维傅里叶变换光谱技术的原理及应用。

II.四波混频实验方案

二维傅里叶变换光谱技术可以在四波混频技术［10-15］或泵浦-探测技术［16，17］的基础上实现。我们这里仅讨论基于四波混频技术实现的情况。在一般的四波混频的实验中，三束脉冲光作为激发光和研究对象相互作用，在二维傅里叶变换光谱技术中还需要第四束脉冲激光作为相位稳定参考脉冲。根据激发光和参考激光在空间的排布位置，可以分为非共线、部分非共线、共线这三种情况。这里我们只讨论非共线的情况，这种情况下，信号和三束激发激光的传播方向完全不一样，所以可以实现无背景探测。一个典型的四波混频的实验如图1所示，四波混频中的三束激发脉冲激发光分别标识为A∗，B和C，其中A∗与B，C相位共轭。四束激光在空间上平行非共线排布，他们的位置在空间中构成了一个立方体的四条棱，我们在样品前的会聚透镜上虚构一个正方形，三束激发脉冲光和一束参考光平行传播，分别垂直入射到该正方形的四个角上。由于相位匹配条件的存在，四波混频的信号光的频率满足ωsig=-ωA+ωB+ωC，而信号光的波矢量满足ksig=-kA+kB+kC，所以会出现在样品后方的会聚透镜的正方形的第四个角上，即和第四束光的传播方向一致。第四束激光被分为两束，一束为参考光，一束为示踪光。示踪光被用于调节光路，它与三束激发激光平行传播，出现在正方形的第四个角上，在实际测量信号时，示踪光被关闭。样品后方，在本应出现示踪光的位置，四波混频信号光被引入光谱仪。参考光在四波混频光路之外传播，最终与四波混频信号光会合进行干涉，光谱仪采集两束光的干涉信号。值得一提的是，在大多数二维傅里叶变换光谱的实验中，第四束激光不会被分成两束而仅作为参考光经过样品，这样做的好处是无需考虑参考光和信号光之间相位差的变化因为参考光和信号光所经过的光学元件等完全一样，但坏处是参考光会激发样品可能对实验结果造成干扰。反之，如果参考光不经过样品，我们需要将参考光和激发激光之间的位相锁定。另外，入射光的偏振方向虽然不会对信号的频率和方向造成影响，但会改变四波混频信号的强度大小和衰减时间，详细的讨论见文献［18］。

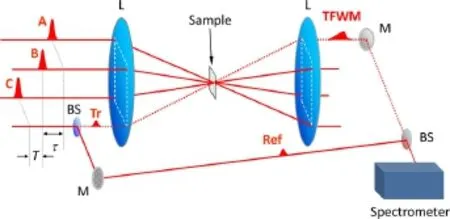
图1.基于四波混频方案的二维傅里叶变换光谱的采集。图中BS标示的是分束镜，M是反射镜，L是透镜。Tr是指示踪光而Ref是指参考光。A，B，C以及Tr和Ref是从同一超快激光器发射出来的脉冲通过分束镜得到的。图中的Spectrometer是一个光栅光谱仪。图来自文献［19］

实验中，我们改变两个脉冲之间的时间延迟，同时记录下每一延迟对应的干涉仪图像，该图像以第一个频率变量为横轴。扫描完成后，全部的数据集通过一个一维数值傅里叶变换将时间延迟变量转换为第二个频率变量，从而得到以两个频率变量为坐标轴以等高线为大小的三维图，即是二维傅里叶变换谱。

实验中所得到的二维谱图与脉冲的激发顺序有关。图2显示了三束脉冲光激发下可采用的激发顺序。脉冲的激发顺序与能够得到的被激发材料的退相位信息密切相关。图2（a）中，第一束与其它两束脉冲光相位互为共轭，这一激发顺序抑制了样品内各分子间相位的不均一性，最终得到光子回波（Photon Echo）信号。这种被称作“复相位（Rephasing）”的激发顺序，最终进行傅里叶变换得到的两个频率变量为ωτ和ωt，这一脉冲顺序在激发的过程中抑制了信号的非均匀展宽。光子回波可以被认为是核磁共振中的自旋回波在光学波段的表现，可以消除光学介质的非均匀展宽的影响从而得到均匀展宽的线宽［20］。图2（b）中的顺序是“复相位”的一种变形，进行傅里叶变换的时间变量为T和t，确保了在第二段时间延迟的扫描中非辐射相干的贡献部分会被探测到［21］。图2（c）中，共轭脉冲位于第二的位置，这种情况与“复相位”激发相反，样品内各分子的不均一性没有被消除，测量得到的是具有非均匀展宽的信号，这种情况被称作“非复相位（Nonrephasing）”。图2（d）中，共轭脉冲作为第三束激光，第二束与第三束光的时间延迟被用于傅里叶变换，这一脉冲顺序被用以研究非辐射相干中的双量子（Two-Quantum）贡献。

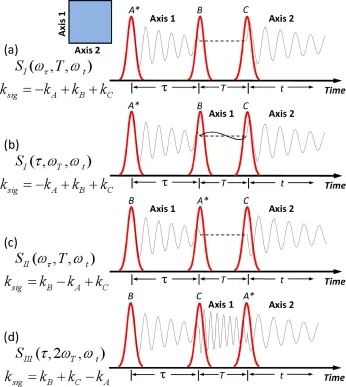
图2.光学2DFT技术中所用的不同的脉冲顺序的示意图。（a）“复相位”的SI技术，（b）代表的是SI技术的一种变形，（c）“非复相位”SII技术，（d）是双量子SIII技术。在每一个小图中，Axis1和Axis2分别和（a）中的插图所显示二维图的Axis1和Axis2相对应。图来自文献［1］

III.锁相的实现

我们用数值计算进行光谱数据的多维傅里叶变换，但是计算时要求实验中信号位相保持稳定。为了满足这一要求，人们发展了被动式稳定方法［10-13］与主动式稳定方法［14，15，22］。在被动方法中使用的核心思路是，稳定的机械结构以及光程共路。可用的方案包括，利用衍射光学元件产生空间分离的脉冲，再利用脉冲整形装置改变各束脉冲的延迟时间长度和相位等。主动式锁相方式是用反馈电路实现脉冲间的相位稳定。现在得到二维光谱的方法已经有很多，但还没有一个方法是完美的，各自有着各自的优缺点，所以人们还在不断地改进试图得到一个可以普遍适用的简单方法。

美国麻省理工的Keith Nelson教授领导的小组使用液晶空间光调制器（Spatial Light Modulator，SLM）进行脉冲整形的方法进行相位稳定［23，24］。一束飞秒脉冲激光被会聚入射到一个方形栅格模式的衍射元件，出射的±1阶衍射光形成一个正方形的四角，这四束光构成了三束激发光和一束参考光。四束光再次经过一个衍射光栅和一个长焦圆柱透镜，进入两维液晶空间光调制器（2D SLM）。SLM的像素点可以用来控制色散光的空间相位与强度，一个线性相位梳用来控制脉冲光的时间延迟。这种方法中，由于四束光光程共路，而避免了各束光之间的光程差抖动。另外还有研究小组用其它调制光的方法实现了脉冲间相位的稳定性从而得到了二维傅里叶变换光谱。

仅用简单的光学元件也是可以实现二维傅里叶变换光谱的采集。因为这类方法十分简单实用也引起了人们的关注，最近几年有几种设想被提出并得以实现。德国维尔茨堡大学的Tobias Brixner小组提出了使用传统光学元件与位移台，不包含衍射和脉冲整形等复杂过程的被动式稳定方法［12］。该方法的主要思想是共路与分束。一束脉冲光经过第一面分束镜分为上下两束，3+4和1+2光，3+4光在经历一个电动位移台之后，与1+2光一同到达方向与第一面分束镜垂直的第二面分束镜，此时两束光分为四束1，2，3和4四束光。1，3光再经过2号位移台，之后四束光一同到达反射式会聚球面镜，经一面折叠式反射镜后，会聚在样品上。虽然避免了各种繁琐的技术，但是该方法的缺点是稳定性不足。另外，德国马普所的Thomas Pfeifer小组最近使用四象限镜实现被动式稳定，不需要使用衍射光学与脉冲整形设备［25］。该方案使用一个具有四个孔的挡板产生四束平行激光。一个具有四块独立可调节的反射镜的装置用来控制四束激光的时间延迟，从而一定程度上保证相位稳定性。

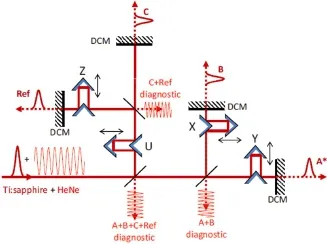
图3.主动锁相式的二维傅里叶变换光谱仪中的内置迈克尔孙干涉仪。A，B，C和Ref是用于产生二维光谱的超快脉冲。氦氖连续激光从二色滤光片（DCM）反射产生干涉条纹，该条纹被用于锁相和光程测量。图来自文献［1］

在主动式稳定中，人们应用了反馈环路来抑制机械漂移带来的影响。使用这一方法的代表为美国科罗拉多大学的Steven Cundiff教授所领导的实验小组［1］。该实验方案中使用的三束激发光与参考、示踪光脉冲，它们之间的时间延迟可以通过控制四个分立的高精度电动位移台来实现。通过改变位移台的位移量，即可改变脉冲之间的时间延迟。此外它们之间必须保持足够的稳定性。实验光学平台以及镜座等各个部分的振动带来的机械漂移会引起光程变化，使得无法保证四波混频信号光与参考光之间的相位稳定，导致无法很好地观测信号光与参考光的干涉信号，因此实验中引入了主动式反馈电路。为了得到任意两束脉冲光之间的相位不稳定的误差信号，使用一束连续激光与所有脉冲光共线传播，构成一套迈克尔孙干涉仪。图3中展示了光路中内置的迈克尔孙干涉仪，拥有三个干涉臂。光路中使用了分色镜（DCM），脉冲激光可以直接通过分色镜，而连续激光会被分色镜反射后形成光路重叠部分。干涉仪得到的误差信号被光电二极管接收输入电子环路滤波电路（Loop Filters），环路滤波电路处理后输出的信号被驱动电路放大用以驱动压电元件。压电元件的振动将实时调整光路光程，从而抵消机械漂移带来的光程改变，最终抑制机械漂移，足以确保任意两束脉冲光之间的相位稳定。这种方法稳定性好，功能强大，可以实现所有二维傅里叶变换光谱类型的采集。缺点是整个系统十分复杂。

IV.在简单原子体系中的应用

由于碱金属原子只有一个外层电子，因而碱金属原子蒸气具有简单的能级结构，理论上比较容易计算，所以成为一个研究光和物质相互作用的理想系统。每一项新的光谱实验技术都会用原子蒸气作为检验和研究的体系。最近的例子包括冷原子［26］、多波混频［27］和电磁感应透明［28］等。对碱金属原子体系中的超快动力学研究也有许多例子，例如传播效应［29，30］，量子干涉［29，31，32］和非马尔科夫过程（non-Markovian）［33，34］的研究。但即使对于碱金属蒸气如此简单的体系，分析和解释其一维光谱有时候还是会有些困难，因为一维光谱往往是几种效应的叠加，这些效应所造成的信号很难在一维光谱中被单独提取出来。而如上所述，二维光谱具有分解不同的量子激发路径的能力，所以用二维光谱研究碱金属原子体系也是一件十分自然的事情。从另一个角度讲，通过对这种简单原子体系的研究，我们可以对比二维光谱的实验和理论从而提高二维光谱的实验或理论的精度。

图4展示了250◦C下用氩做缓冲气的钾蒸气的两种2DFT光谱，SI（ωτ，T，ωt）和SII（ωτ，T，ωt）［19］。横轴频率是通过记录参考脉冲光与四波混频信号的干涉图样直接得到，竖轴通过对延迟时间τ的快速傅里叶变换得到。如引言中所示，SI（ωτ，T，ωt）和SII（ωτ，T，ωt）可以用以确定均匀展宽和非均匀展宽的线宽。但在当前的实验条件下，均匀展宽和非均匀展宽的线宽是很接近的，所以各个峰是比较对称的。

每一张谱图包含两个位于对角线上的信号峰，它们对应了钾的D1（42S1/2→42P1/2）和D2（42S1/2→42P3/2）跃迁，此外还有与对角线正交方向的两个信号峰，它们代表了D1和D2的耦合。利用费曼图［35］，可以得到SI（ωτ，T，ωt）和SII（ωτ，T，ωt）图谱中各个峰对应的量子路径，从而定性地解释它们之间的相对信号强度。这个量子系统中的双边费曼图如图5所示，可以看出SI（ωτ，T，ωt）图中的每个峰对应两条激发路径，而SII（ωτ，T，ωt）中的对角峰（NA和NB）对应三个激发路径，非对角峰对应一个激发路径。一般来说，信号峰的强度和参与激发路径的贡献的总和成正比，而每条激发路径对信号所做的贡献与每一步的跃迁偶极距大小的总乘积成正比。这样，我们可以得到SI（ωτ，T，ωt）中峰的强度比为RA：RC：RD：RB=1：2：2：4，而SII（ωτ，T，ωt）中的峰的强度比NA：NC：ND：NB=2：1：1：5。这个分析结果是和实验结果符合的。

图4.（a）激发脉冲的频谱（红色虚线），250摄氏度下的钾蒸气的实验测得的吸收谱（黑色点线）和计算的吸收谱（蓝色实线）。α是吸收系数，L是吸收长度。（b）与实验相关的钾原子的能级位置，能级的能量单位是THz。（c）SI（ωτ，T，ωt）信号的振幅的实验谱图（下图）和SII（ωτ，T，ωt）信号的振幅的实验谱图（上图）。（d）SI（ωτ，T，ωt）信号的实部的实验谱图（下图）和SII（ωτ，T，ωt）信号的实部的实验谱图（上图）。谱图都是按照谱图中最强的峰值归一化。图来自文献［19］

通过光学Bloch方程，也可以对光谱结果进行理论上的数值模拟，数值模拟结果与实验结果拥有很好的一致性。在SI和SII谱图中，峰的线形主要为吸收型，只有少量的色散成分。如果将SI（ωτ，T，ωt）和SII（ωτ，T，ωt）信号叠加，则可以获得纯的吸收型信号峰并且谱图的分辨率得到了提高。

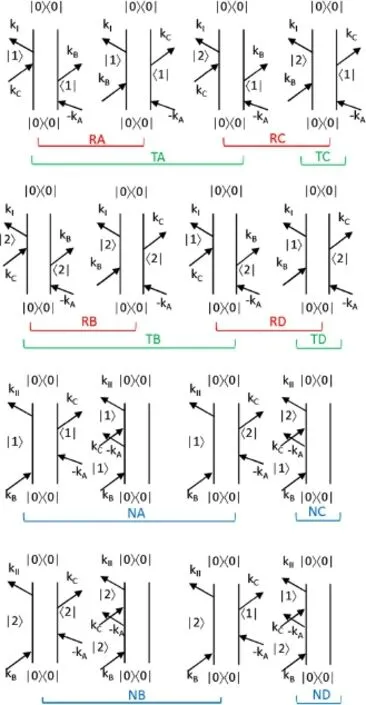
图5.表示V类型能级系统中所有对三阶光响应有贡献的跃迁路径的双边费曼图。上面两行的路径图对应的是SI（ωτ，T，ωt）谱图和SI（τ，ωT，ωt）谱图中的跃迁而下面两行的路径图对应的是SII（ωτ，T，ωt）谱图中的跃迁。标示电子态的数字0，1和2对应于钾原子的42S1/2，42P1/2和42P3/2态。图来自文献［19］

如上所述，SI（ωτ，T，ωt）的谱图中的非对角峰对应两条激发路径的贡献，基态漂白（Ground-State Bleaching）和激发态发射（Excited-State Emission）。这两条路径在延迟时间T内是不同的，在第二束脉冲激光与体系相互作用后，基态漂白使体系回到基态而激发态发射使得体系处于42P1/2和42P3/2的叠加态。所以对延迟时间段T的信号而不是延迟时间τ的信号做傅里叶变换，可以将两个路径造成的贡献区分开来，也就是说SI（τ，ωT，ωt）谱图可以将激发态发射这一类型的贡献分离出来。激发态发射这个路径描述的是D1和D2通过共同的基态所产生的耦合，所以也被称为“拉曼型”的路径。图6是一个SI（τ，ωT，ωt）的实验谱图。在实验中，τ=0。从该谱图中可以看到在零能量处有两个强峰，还有两个较弱的边峰（TC和TD）。这两个边峰代表的就是拉曼型的激发路径的贡献。

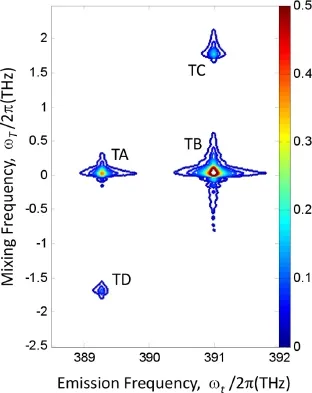
图6.SI（τ，ωT，ωt）的实验谱图。图中的各个峰对应的跃迁路径显示在图5中。图来自文献［19］

如引言中所述，还有一类二维傅里叶变换光谱是共轭脉冲作为第三束激光，第二束与第三束光的时间延迟被用于傅里叶变换，得到的谱图记为SIII（τ，2ωT，ωt）。这种谱图显示的是体系中双量子相干信号，比如双光子跃迁或者不同原子或分子之间相互作用造成的信号。用钾原子作为样品所得到的SIII谱图［36］如图7（a）所示，谱图的纵轴显示的是对应两倍光子能量左右而横轴显示的对应一个光子能量左右的信号。从图4（b）上可以看出，两个光脉冲的总能量不能将钾原子的基态和其它任何能级耦合，但在SIII谱图中，共振峰的信号却很明显。共振峰的纵轴的位置分别为2ED1，ED1+ED2和2ED2，这里ED1和ED2分别是D1和D2线的跃迁能量。这意味着这些共振峰的信号来自于两个原子通过相互作用对激光的共同响应。但是它们之间的相互作用应该很弱，不然的话这些共振峰的位置应该会偏离两个原子能量的简单叠加。我们可以用凝聚态理论中的激子来描述和解释这个结果，两个处于基态的原子可以被看作是一个激子（Exciton）的基态。如果其中一个原子被激发到第一激发态如42P1/2或42P3/2，可以看作是该激子的单激发态。如果两个原子都处于激发态并通过偶极-偶极相互作用耦合在一起，那么可以被看作该激子的双激发态。用这种激子的模型，我们可以来数值模拟双量子和单量子的二维光谱，数值模拟的结果如图7（c）和7（d）所示，可以看出模拟结果和实验结果是符合的。如果在数值模拟中去掉偶极-偶极相互作用，我们就不能得到双量子型的二维光谱。这也说明了二维傅里叶变换光谱技术还可以用来研究量子系统中不同原子或分子的相互作用，并且它的灵敏度是非常高的。

二维傅里叶变换光谱还可以被推广到三维傅里叶变换光谱。一份SI（ωτ，T，ωt）2DFT光谱是通过对于时间延迟τ扫描并进行快速傅里叶变换获得的。如果对τ和T都做扫描并进行变换，那么得到的结果会具有三个频率维度，从而得到三维傅里叶变换（3DFT）谱图［37］。3DFT相比2DFT的优势在于，它在测量三阶非线性吸收方面，进一步分离了信号中一些2DFT无法分离开的不同的量子路径。

我们知道，2DFT光谱的峰形在对角线方向上的展宽代表了非均匀加宽，然而实验测量的是透射光信号，则脉冲传播效应会伴随着激发光与信号光一同导致光谱线形在水平和垂直方向上的形变。倘若将来我们在研究新样品复杂系统的多维傅里叶光谱时，需要样品具有较高的光密度，或是需要提高样品厚度以提高信噪比，则对于传播效应的研究，可以帮助人们隔除传播效应带来的不良影响，从而更加专注于对于物理问题的研究。

选用能级系统简单的碱金属原子蒸气为样品就可以很容易研究脉冲传播效应对2DFT光谱图的影响［38］。在实验变量方面，通过控制样品池的加热温度，即可改变池中原子蒸气的密度，从而控制样品的光密度。在适当的光密度下，光谱会变形加宽，光密度过高时，光谱甚至会出现劈裂。另一方面，实验中控制使参考光绕过样品或者穿过样品，两种情况下的实验结果证明传播效应既会发生在激发光上，也会发生在信号光上。参考光与信号光一同经过样品，则能够补偿传播效应对于信号光的影响，修正这一因素导致的光谱变形，但是这样的方法并不能弥补激发光的传播效应影响。最后一个实验条件的选择，是控制三束激发光的重叠中心在样品池中的位置。当激发光的重叠中心靠近样品池的入射面，这时激发脉冲带来的传播效应变小，信号光的传播效应加强，结果表现为光谱在横轴方向表现出一定的变形，在竖轴方向，变形很小；当重叠中心向样品池的出射面靠近时，激发光经历的传播距离变大，传播效应加强，导致光谱线形在垂直方向上的形变加大。因此我们有时也将横轴称为辐射轴，竖轴称为吸收轴。对于传播效应的研究能够帮助我们在利用2DFT技术进行实验时，考虑到不同的实验条件所引起的传播效应对于实验光谱的影响，从而帮助我们选择最佳的实验条件，最终获得受影响最小形变最轻的实验光谱。

图7.实验获得的双量子（a）和单量子（b）的二维光谱和它们对应的数值模拟图（c）和（d）。所有二维光谱显示的均为二维光谱的实部。D1和D2分别对应于钾原子的42S1/2→42P1/2和42S1/2→42P3/2的跃迁频率。图来自文献［36］

V.利用2DFT对量子阱的研究

直接带隙半导体在光电领域具有很重要的地位，因为直接带隙半导体具有将光转化为激发电子或是进行反向过程的能力，因而被应用于制造发光设备与光电探测器，这些设备被广泛应用于当今人们的生产生活以及科学研究中。在超快激光被用于研究半导体之后，人们逐渐发现多体效应在半导体的非线性光学测量中起到的影响不容忽视，比如理论计算结果显示多体效应会使半导体激光的增益峰发生移动［39］。因而我们需要研究半导体内部的多体效应，以此来了解多体效应在光与半导体发生作用时产生的影响，同时也能够加深对于多体作用本身的理解［40］。

半导体在吸收光子之后会产生出电子-空穴对，因为一个电子由价带进入了导带。电子空穴对受库仑力束缚，便形成了激子。类似于氢原子，我们可以用相对坐标来描述激子，然而激子的质量中心却远远偏离了位于坐标中心的空穴。由于激子质量过小，并且具有很高的介电常数，导致体系的结合能大小只有毫电子伏量级，因而激子只存在于低温条件之下。在低温条件下，激子对激发光的共振主导了直接带隙半导体在带边缘的吸收和发射谱。

最一般的直接带隙半导体就是砷化镓（GaAs）。砷化镓易于获得，稳定的外延生长技术可以用来生成高质量异质结构的砷化镓。砷化镓的带隙对应着近红外波长，实验使用的激光易于产生。美国科罗拉多大学的Steven Cundiff教授领导的小组在实验中使用的约10 nm的砷化镓薄层生长在两层铝镓砷（AlGaAs）之间［41］。在直接带隙附近，砷化镓拥有两个价带，即为重空穴和轻空穴带。量子限域效应使得在块状砷化镓下本应简并的两个价带分离开来。因而低温下的砷化镓量子阱的线性吸收光谱拥有两个峰。图8（a）中实线所示的即为重空穴和轻空穴两个吸收峰，虚线表示的则是激发光光谱。

在过去20年中，相干光谱学一直被应用于研究半导体中的激子［42］。在研究中人们逐渐发现实验信号其实是由多体效应主导的，因而多体作用成为了研究工作的首要目标。此外，尽管半导体的生长工艺不断成熟完善，纳米尺度的层状结构半导体在厚度上仍然会有起伏，而厚度的波动导致了实验观测到的信号具有非均匀展宽。因而人们在对量子阱的2DFT实验中着力于使用一系列手段来研究样品中的多体效应以及消除光谱中的非均匀展宽。

回顾前文所述，四波混频使用的三束激发脉冲光由波矢ka，kb和kc表示，三束脉冲之间的时间延迟分别为τ，T和t。根据ka，kb和kc不同的先后到达顺序，我们有对应的光谱Si。最通常的“复相位”SI（ωτ，T，ωt）光谱，能够帮助我们得到信号的均匀展宽宽度，并且SI（τ，ωT，ωt）能够使我们分离出一维光谱中无法分辨的拉曼相干成分；“非复相位”光谱SII（ωτ，T，ωt）能够隔离基态漂白引起的耦合；SIII（τ，ωT，ωt）则能够分离出双量子相干的成分。

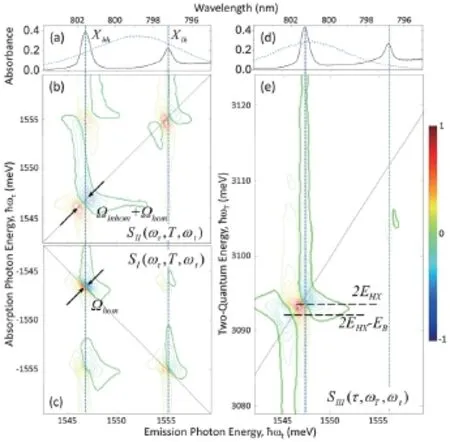
图8.（a）和（d）GaAs量子阱的线性吸收谱图。虚线显示的是激发脉冲的频谱。图（b）和（c）分别显示的是GaAs量子阱的“非复相位”SII（ωτ，T，ωt）和“复相位”SI（ωτ，T，ωt）的2DFT谱。图（e）显示的是SIII（τ，ωT，ωt）谱图。各个2DFT谱图显示的均为信号的实部并均根据最强的峰值归一化。图来自文献［1］

图8（b）和（c）显示的分别是共线线偏振SI（ωτ，T，ωt）和SII（ωτ，T，ωt）的实部光谱，光谱中在对角线方向上的两个对角峰，分别对应了重空穴和轻空穴激子的信号峰。对于一个简单的多能级系统，实的SI（ωτ，T，ωt）显示的是系统的吸收线形，信号强度应该全部为正值。然而实验结果中的重空穴峰线形是色散型的，这主要是缘于多体效应带来的影响［43，44］。与对角线正交的方向出现的峰，是由于激子间的多体相互作用而产生的，它们的强度总是弱于对角峰的［9］。重空穴峰在对角线方向上的延伸则是缘于非均匀展宽，而半导体量子阱的非均匀展宽是由于阱宽的浮动造成的。即量子限域能量反比于阱宽，阱宽的波动造成了能量的浮动。通过比较SI（ωτ，T，ωt）和SII（ωτ，T，ωt）的方法，可以同时得到均匀和非均匀谱宽［45］。

当第一束脉冲光的偏振方向与其他脉冲的偏振正交，而不改变其他的实验条件时，我们能够得到正交偏振的“复相位”光谱SI（ωτ，T，ωt）。在正交偏振的SI（ωτ，T，ωt）光谱中，四波混频产生的信号光的偏振与第一束脉冲偏振方向相同，同时整体的信号强度也减弱了。重空穴激子对角峰的形状以及它相对于激子分子峰的强度发生了巨大变化，现在的线形是吸收型的。这些变化是由于正交偏振激发光抑制了光谱中多体效应的贡献。在受到正交偏振的激发光作用后，样品内的布居分布形成了布居光栅，即是指自旋不同的激子在空间上的交替分布。然而多体相互作用是出于相同自旋的激子之间的相互作用，要求不同自旋的态在空间上均匀分布，因此布居光栅抑制了量子阱内的多体效应。正交偏振的SI（ωτ，T，ωt）谱验证了以上推论。

与钾原子蒸气类似，选择合适的激发次序，GaAs量子阱的二维谱图也可以分离出非辐射相干，即不能由电偶极跃迁耦合的两个态之间的相干。这样的跃迁不能直接在光的作用下产生，在一维的光谱中，我们无法分离出非辐射相干的贡献。在GaAs量子阱中，有两种非辐射相干的具体表现，“拉曼”相干和“双量子”相干。

第一种非辐射相干，是指重空穴与轻空穴态之间的相干［46-48］，这两个态的能量十分接近，因而这种相干被称作“拉曼（Raman）”相干。图8（c）中的非对角峰，实际上就包含有“拉曼”相干的成分，以及两个激子通过基态漂白产生的耦合。如果实验中改为扫描第二个时间延迟T，从而得到SI（τ，ωT，ωt）光谱，那么与对角线相正交方向上的信号峰将只包含有“拉曼”相干。由拉曼峰的宽度则可以了解到散射过程导致的两个激子态间的相对能量。

另一种非辐射相干是指基态与一个经过两次激发的态的相干，比如基态与激子分子的相干［23，49］，这种相干被称作双量子（Two-Quantum）相干。与碱金属原子的情况类似，SIII（τ，ωT，ωt）谱图同样可以被用来观察GaAs量子阱中的双量子相干。实验期望观测基态与一个激子分子态的相干，然而双量子相干中会涉及与两次激发的多体态的耦合［23，24，50］。实验中使相位共轭的脉冲A*第三个到达，此时前两个脉冲已经使系统中产生了经过两次激发的态。第三束脉冲既有可能使基态与一个一次激发态发生辐射相干，也有可能使一次激发态与两次激发态发生相干。因此双量子相干只存在于第二段时间延迟T中，我们对时间延迟T做傅里叶变换，当ωT≈2ωt时可以发现双量子相干，此外还有基态与多体态的双量子相干。图8（e）所展示的即是GaAs量子阱的SIII（τ，ωT，ωt）谱图。实验中使用的激发光具有圆偏振，且第一束激发脉冲与后两束脉冲圆偏振方向相反。双量子共振发生的能量对应图中纵坐标ħωT等于2EHX-EB的位置，其中EHX表示重空穴态的共振能量，EB表示激子分子的结合能。此外ħωT等于2EHX处的信号峰则被归属于涉及多体态的双量子相干。如果改变实验条件，使第一束激发光的圆偏振同两外两束激发光一致，则得到的SIII（τ，ωT，ωt）谱图中，将只含有多体态的双量子相干，激子分子的双量子相干被抑制了。这样的实验结果验证了我们对于信号的归属。

VI.其它量子体系中的应用

红外波段以及近红外波段的二维傅里叶变换光谱在化学领域有着许多重要的应用。这里近红外波段的二维傅里叶变换光谱的方法和技术在本文前面讨论过的一样，而在红外波段工作的二维傅里叶谱由于激发激光波长较长，通常采用被动式稳定相位的方法即可，但由于工作在红外波段，光源和探测通常是实验技术的难点所在。二维傅里叶变换光谱方法常被用来研究平衡态下快速的分子变化，分子间相互作用（如氢键，偶极-偶极相互作用等）在常温液体里的动态变化，水氢键网络的演变过程，小分子、多肽和蛋白的静态或瞬间结构变化［2-6，51-55］。这些研究极大的丰富了人们对各种体系中化学过程的认识。由于已经有许多有关这方面的详尽的综述，这里我们就不再详细讨论。

VII.总结和展望

激光自其诞生以来，随着其技术的飞速发展，光谱学有了巨大的进步并且发展出了广泛的分支领域。然而将超快脉冲激光与多维傅里叶变换谱相结合，所得到的光谱技术展现了其非常新颖与强大的特点。多维傅里叶变换光谱突破了传统一维光谱技术的限制，使得我们可以获得量子系统演化动力学的信息。作为一种能够对量子系统进行更深入与细致分析的光谱学手段，推广其应用于更多、更复杂的材料与量子体系的研究成为了这项技术的一个发展方向。

在本文中我们主要介绍了多维傅里叶变换光谱的基本原理与典型的实验方案。在完全非共线空间布局下由四波混频实现的二维傅里叶变换光谱，这种实验方案相较于共线与半共线方案，从根本上去除了信号光的背景成分。然而傅里叶变换光谱对于各束激发光之间相对相位的稳定性有较高要求，促使实验上发展了多种相位稳定方法。本文所介绍的由反馈电路系统实现的主动式锁相方法，可以保证任意两束激发光以及激发光与参考光之间的相对相位稳定，是一种非常强大方案。主动式锁相相较于被动式锁相，可以实现更优秀的相位稳定性，然而整套实验装置复杂度高，搭建与调节需要投入的成本非常巨大。使用被动式锁相的各类方案，在保证一定的相位稳定性的同时，更容易搭建与实现。简化实验方案，降低实验搭建难度，同时保证一定的相位稳定性，成为了多维傅里叶变换光谱技术的一大发展方向。投入产出比的不断提高，也将成为多维傅里叶变换光谱取代普通光谱技术，获得更大推广的动力之一。

致谢

本工作由国家重大科学研究计划（编号：2013CB922003）和国家自然科学基金（批准号：11474178）资助。

参考文献

［1］Bristow A D，Karaiskaj D，Dai X，Zhang T，Carlsson C，Hagen K R，Jimenez R，Cundiff S T.Rev.Sci. Instrum.，2009，80（7）：073108

［2］Cho M.Chem.Rev.，2008，108（4）：1331-1418

［3］Hamm P，Lim M，Hochstrasser R M.J.Phys.Chem. B，1998，102（31）：6123-6138

［4］Asplund M C，Zanni M T，Hochstrasser R M.PNAS，2000，97（15）：8219-8224

［5］Golonzka O，Khalil M，Demirdven N，Tokmakoff A.Phys.Rev.Lett.，2001，86（10）：2154-2157

［6］Sul S，Karaiskaj D，Jiang Y，Ge N.J.Phys.Chem. B，2006，110（40）：19891-19905

［7］Hybl J D，Albrecht A W，Gallagher Faeder S M，Jonas D M.Chem.Phys.Lett.，1998，297（3）：307-313

［8］Tian P，Keusters D，Suzaki Y，Warren W S.Science，2003，300（5625）：1553-1555

［9］Borca C N，Zhang T，Li X，Cundiff S T.Chem.Phys. Lett.，2005，416（4-6）：311-315

［10］Cowan M L，Ogilvie J P，Miller R J D.Chem.Phys. Lett.，2004，386（1-3）：184-189

［11］Brixner T，Stiopkin I V，Fleming G R.Opt.Lett.，2004，29（8）：884-886

［12］Selig U，Langhojer F，Dimler F，Lohrig T，Schwarz C，Gieseking B，Brixner T.Opt.Lett.，2008，33（23）：2851-2853

［13］Vaughan J C，Hornung T，Stone K W，Nelson K A. J.Phys.Chem.A，2007，111（23）：4873-4883

［14］Volkov V，Schanz R，Hamm P.Opt.Lett.，2005，30（15）：2010-2012

［15］Zhang T，Borca C，Li X，Cundiff S.Opt.Express，2005，13（19）：7432-7441

［16］Myers J A，Lewis K L，Tekavec P F，Ogilvie J P. Opt.Express，2008，16（22）：17420-17428

［17］Shim S，Zanni M T.Phys.Chem.Chem.Phys.，2009，11（5）：737-834

［18］Cundiff S T，Wang H，Steel D G.Phys.Rev.B，1992，46（11）：7248-7251

［19］Dai X，Bristow A D，Karaiskaj D，Cundiff S T.Phys. Rev.A，2010，82（5）：052503

［20］Shen Y R：The Principles of Nonlinear Optics.New York：John Wiley&Sons（1984）

［21］Yang L，Zhang T，Bristow A D，Cundiff S T，Mukamel S.J.Chem.Phys.，2008，129（23）：234711

［22］Lepetit L，Joffre M.Opt.Lett.，1996，21（8）：564-566

［23］Stone K W，Gundogdu K，Turner D B，Li X，Cundiff S T，Nelson K A.Science，2009，324（5931）：1169-1173

［24］Stone K W，Turner D B，Gundogdu K，Cundiff S T，Nelson K A.Accounts.Chem.Res.，2009，42（9）：1452-1461

［25］Zhang Y，Meyer K，Ott C，Pfeifer T.Opt.Lett.，2013，38（3）：356-358

［26］Bloch I，Dalibard J，Zwerger W.Rev.Mod.Phys.，2008，80（3）：885-964

［27］楼兰，问峰，秦勐哲，贺嘉楠，张彦鹏，肖敏.物理学进展，2013，33（3）：87-135.

［28］Fleischhauer M，Imamoglu A，Marangos J P.Rev. Mod.Phys.，2005，77（2）：633-673

［29］Kinrot O，Prior Y.Phys.Rev.A，1994，50（3）：R1999-R2002

［30］Kinrot O，Prior Y.Phys.Rev.A，1995，51（6）：4996-5007

［31］Golubb J E，Mossberg T W.J.Opt.Soc.Am.B，1986，3（4）：554-559

［32］Shen F，Gao J，Senin A A，Zhu C J，Allen J R，Lu Z H，Xiao Y，Eden J G.Phys.Rev.Lett.，2007，99（14）：143201

［33］Lorenz V O，Cundiff S T.Phys.Rev.Lett.，2005，95（16）：163601

［34］Lorenz V O，Mukamel S，Zhuang W，Cundiff S T. Phys.Rev.Lett.，2008，100（1）：013603

［35］Mukamel S.Ann.Rev.Phys.Chem.，2000，51：691-729

［36］Dai X，Richter M，Li H，Bristow A D，Falvo C，Mukamel S，Cundiff S T.Phys.Rev.Lett.，2012，108（19）：193201

［37］Li H，Bristow A D，Siemens M E，Moody G，Cundiff S T.Nat.Commun.，2013，4：1390

［38］Li H，Spencer A P，Kortyna A，Moody G，Jonas D M，Cundiff S T.J.Physs Chem.A，2013，117（29）：6279-6287

［39］Chow W，Koch S，Sargent M：Semiconductor-laser Physics.Berlin：Springer-Verlag（1994）

［40］Chemla D S，Shah J.Nature，2001，411（6837）：549-557

［41］Cundiff S T，Zhang T，Bristow A D，Karaiskaj D，Dai X.Accounts.Chem.Res.，2009，42（9）：1423-1432

［42］Cundiff S T.Opt.Express，2008，16（7）：4639-4664

［43］Li X，Zhang T，Borca C N，Cundiff S T.Phys.Rev. Lett.，2006，96（5）：057406

［44］Zhang T，Kuznetsova I，Meier T，Li X，Mirin R P，Thomas P，Cundiff S T.PNAS，2007，104（36）：14227-14232

［45］Kuznetsova I，Meier T，Cundiff S T，Thomas P. Phys.Rev.B，2007，76（15）：153301

［46］Ferrio K B，Steel D G.Phys.Rev.Lett.，1998，80（4）：786-789

［47］Spivey A G V，Borca C N，Cundiff S T.Solid State Commun.，2008，145（5-6）：303-307

［48］Hawkins S A，Gansen E J，Stevens M J，Smirl A L，Rumyantsev I，Takayama R，Kwong N H，Binder R，Steel D G.Phys.Rev.B，2003，68（3）：035313

［49］Ferrio K B，Steel D G.Phys.Rev.B，1996，54（8）：R5231-R5234

［50］Yang L，Mukamel S.Phys.Rev.Lett.，2008，100（5）：057402

［51］Zheng J，Kwak K，Fayer M D.Accounts.Chem.Res.，2007，40（1）：75-83

［52］Fayer M D，Moilanen D E，Wong D，Rosenfeld D E，Fenn E E，Park S.Accounts.Chem.Res.，2009，42（9）：1210-1219

［53］Elsaesser T.Accounts.Chem.Res.，2009，42（9）：1220-1228

［54］Ginsberg N S，Cheng Y，Fleming G R.Accounts. Chem.Res.，2009，42（9）：1352-1363

［55］Jansen T L C，Knoester J.Accounts.Chem.Res.，2009，42（9）：1405-1411

The concept of two-dimensional or multidimensional Fourier-transform（2DFT or MDFT）spectroscopy originated from nuclear magnetic resonance（NMR）spectroscopy.the development of femtosecond laser technology allows the MDFT spectroscopy to be extensively implemented in optics in recent years，where the conventional radio frequency（RF）field in the NMR is replaced by pulse lasers with wavelength ranging from infrared to visible domain.The optical MDFT spectroscopy can be used to identify the population of each quantum state and the coupling between quantum states，thus to determine the evolutionary dynamics of quantum system，such as energy transfer in quantum systems and molecules interactions，in addition to the information obtained from one-dimensional spectroscopy.The optical MDFT spectroscopy has been successfully applied in the studies of a variety of quantum systems including alkali atoms，quantum wells，molecules，etc.

Optical Multidimensional Fourier-transform Spectroscopy

Zhao Wei，Zhou Zhao-Yu，Yang Jin-Xin，Dai Xing-Can
State Key Laboratory of Low-Dimensional Quantum Physics，Department of Physics，Tsinghua University，Beijing 100084

Two-dimensional Fourier-transform spectroscopy；Four-wave mixing；Ultrafast pulse laser；Phase lock

date：2015-05-05

O43

A

10.13725/j.cnki.pip.2015.04.002

*XingcanDai@mail.tsinghua.edu.cn

1000-0542（2015）04-0178-11177