智能轮式机器人离散模糊自适应PID控制研究
张文君,盛维涛,袁宇鹏,李晓龙
(1. 四川工程职业技术学院,德阳 618000;2. 重庆大学 自动化学院,重庆 400044)
0 引言
移动机器人是一种在复杂环境下工作的,具有自行组织、自主运行、自主规划的智能机器人[1],它融合了计算机技术、信息技术、通信技术、微电子技术和机器人技术等。智能轮式机器人是一种典型的移动机器人,广泛运用于仓库运输、博物馆向导[2]、变电站巡检等场合[3]。
智能轮式机器人运动系统的实时、有效控制是智能轮式机器人执行任务的必要保障。PID控制是过程控制中最通用的控制方法,PID控制器及其改进型控制器是工业过程控制等领域最常见的控制器[4]。然而,由于智能轮式机器人具有高度的非线性、强时变性的特点,常规的PID控制方法已经无法完成有效的控制的。因此,在轮式机器人运动系统的控制领域,许多专家学者致力于改进型的PID控制。D. Shen等[5]针对机器人运动控制系统,提出了一种基于李雅普诺夫的自适应PID控制方法。丁度坤等[6]针对喷涂机器人提出了一种基于最小二乘法的自适应PID控制方法。李冬等[7]将PID与神经网络技术结合,提出BP神经网络PID控制器来处理机器人运动控制问题。
当今社会的控制领域中,几乎所有的控制器均是采用数字控制技术,因此离散式控制方法在现代控制领域凸显了十分重要的地位。本文在常规连续式PID基础上,采用了一种离散式的PID控制器,并且结合了操作简单、易于实现的模糊推理理论。在分析了智能轮式机器人运动系统的动力学模型的基础上,推导出了运动控制系统的连续式和离散式系统控制模型,进而提出了离散式模糊自适应PID控制算法,并通过MATLAB仿真验证了控制算法的有效性。
1 智能轮式机器人动力学理论研究
本文针对的巡检类小型三轮智能移动机器人主要可实现小型变电站巡检、图书馆类巡视等的任务,工作环境相对平整,因此选用的是一类三轮可移动式机器人,如图1所示。图中AL和AR分别表示左右后轮,BL和BR分别表示带动左右后轮转动的电机,C为前轮。移动机器人的驱动来源是两后轮差速驱动,前轮为万向轮仅起到辅助导向以及平衡本体的功能。

图1 轮式移动机器人运动转向系统结构示意图
智能轮式移动机器人的运动转向系统可表征为典型的复杂系统,具有非线性、强时变性的特点。因此,为建立智能轮式移动机器人运动转向系统的动力学模型,本文提出了如下假设:1)车轮与地位运行形式仅为纯滚动,无打滑行为;2)左右后轮保持精确同心;3)不考虑道路粗糙度以及障碍物对于机器人运动的影响。
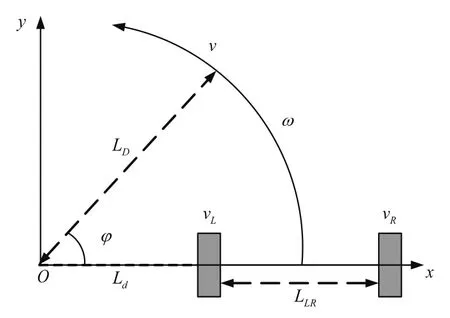
图2 后驱左右轮运动示意图
地面运行时,轮式移动机器人的运动行为可分解为直线、旋转两类。两类运动行为的时空叠加组合可表现为移动机器人地面空间上的直线运动、曲线运动、原地转弯等行为。智能轮式移动机器人的运动行为示意图如图2所示。在笛卡尔坐标系下,智能轮式移动机器人的运动方程可表示为:
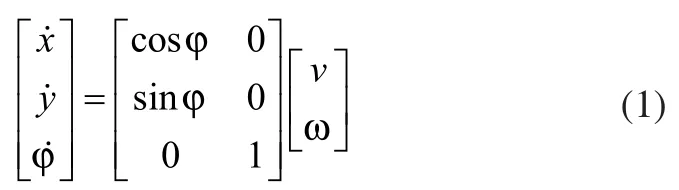
其中x,y和φ分别表示移动机器人左右后轮的质心坐标与角度,移动机器人的位姿状态为,v为直线运动速度,ω为旋转角速度。
本文的智能移动机器人的后轮运动工作在差速驱动模式下,可通过以机器人左右轮不同的速度实现各类基本运动行为,此种控制方式简单,易于操作。令左右后轮的半径为DL、DR,则左右轮的速度可表示为:
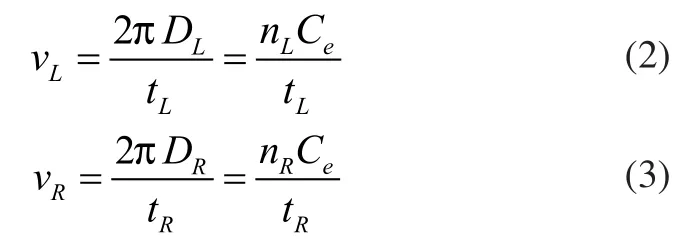
其中vL和vR为左右轮的运动速度,nL和nR分别表示左右轮的编码脉冲数量,Ce为轮子速度系数,tL和tR为左右轮旋转一周的时间。
若假设轮式移动机器人满足刚体运动规律,根据车轮的物理约束条件可建立如下速度方程:
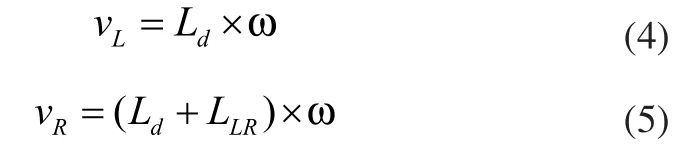
其中Ld为左轮与原点的直线距离,LLR为左右轮之间的直线距离。因此,由式(2)和式(3)可以推导出左右轮中心点的运动速度和旋转速度:
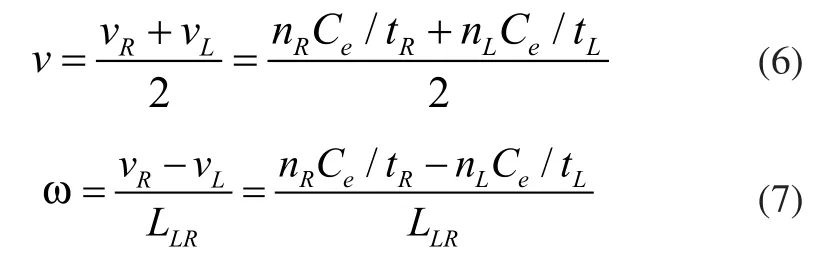
综上所述,轮式移动机器人运动过程中,通过实时控制左驱动轮和右驱动轮的速度即可调节轮式移动机器人的运动速度与旋转角度,进而实现预期的移动机器人位置、姿态与空间定位。对于轮式移动机器人的控制而言,通常均是通过数字控制的方式实现差速驱动转向,对于驱动轮转速变换进行数字式离散化高速运算,进而满足连续调节、精确控制的效果。
2 轮式机器人运动系统的控制模型
通过上文中的动力学理论分析,智能轮式机器人的运动系统的连续式传递函数可表示为[7]:
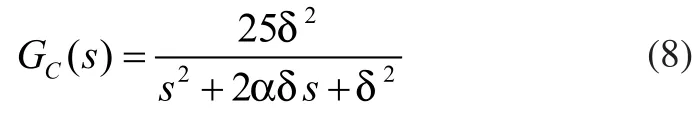
其中0.2α=,18δ=。为进行数字式仿真,同时为了保证系统离散脉冲函数不出现两个及以上的假性零点,本文以采样时间Ts=0.1s将以上连续式传递函数通过输入端的零阶保持器(ZOH)改写成离散形式的脉冲传递函数:
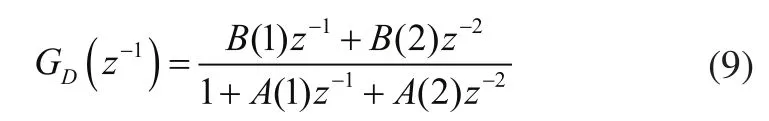
3 轮式机器人运动系统的离散式模糊自适应PID控制器
本节阐述了模糊自适应数字PID控制器的原理,并描述了详细的设计过程。
3.1 模糊自适应数字PID控制器原理
常规数字式PID控制器控制算法可表示为:
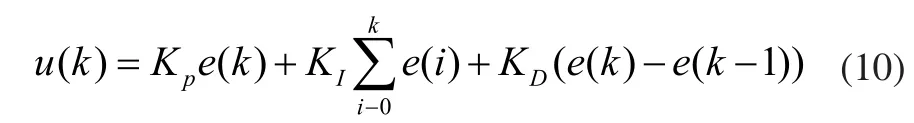
因此,可导出常规增量式数字PID控制算法表达式:
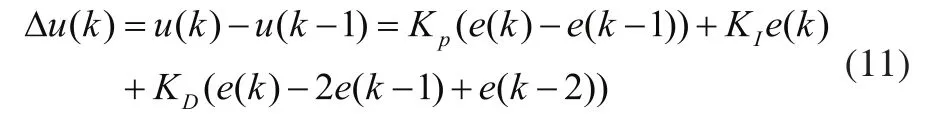
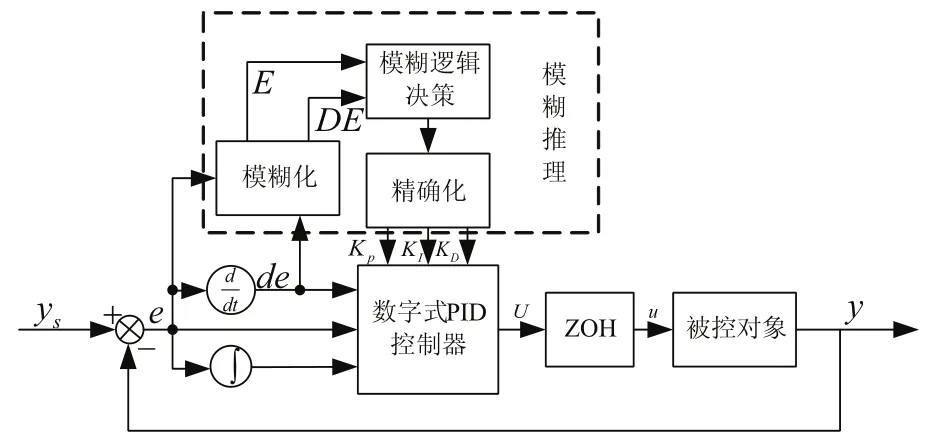
图3 离散模糊自适应PID控制器原理图
模糊自适应数字PID控制器原理如图3所示。模糊自适应数字PID算法结合了模糊推理理论与PID控制算法的特点,能够根据相关先验知识,实时在线辨识出数字式PID控制器参数,从而提升控制器的自适应的能力。图3中首先将误差e与误差导数de经过模糊推理的模糊化处理,得到E和DE。然后基于模糊规则库进行模糊推理决策推理出数字式PID参数并再利用逆模糊化处理进而得到数字式PID控制的实时控制参数KP、KI和KD,从而实现控制输出的自适应调节。
3.2 模糊自适应数字PID控制器设计
针对实际对象的模糊推理控制器的设计过程的关键在于基于设计人员的先验知识和实际经验,建立模糊推理规则表。为在线调节PID控制器的三个参数,通过分析pKΔ、IKΔ和DKΔ对于机器人运动控制系统输出的影响及专家经验,利用IF-THEN语言,获取pKΔ、IKΔ和DKΔ参数的模糊规则,本文的模糊自适应数字PID控制器参数的模糊规则表如表1~表3所示[8]。
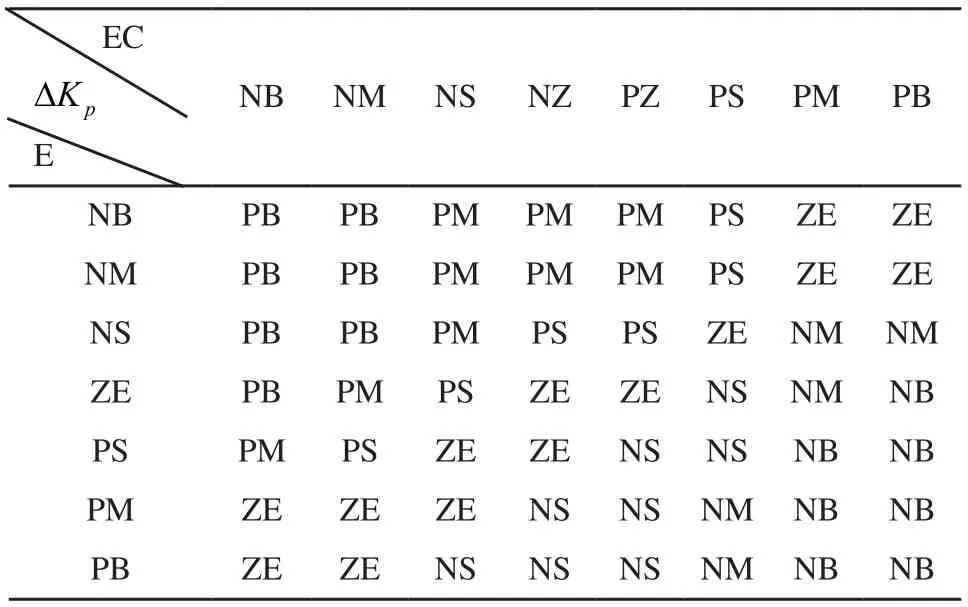
表1 PID参数中pKΔ的模糊推理规则表
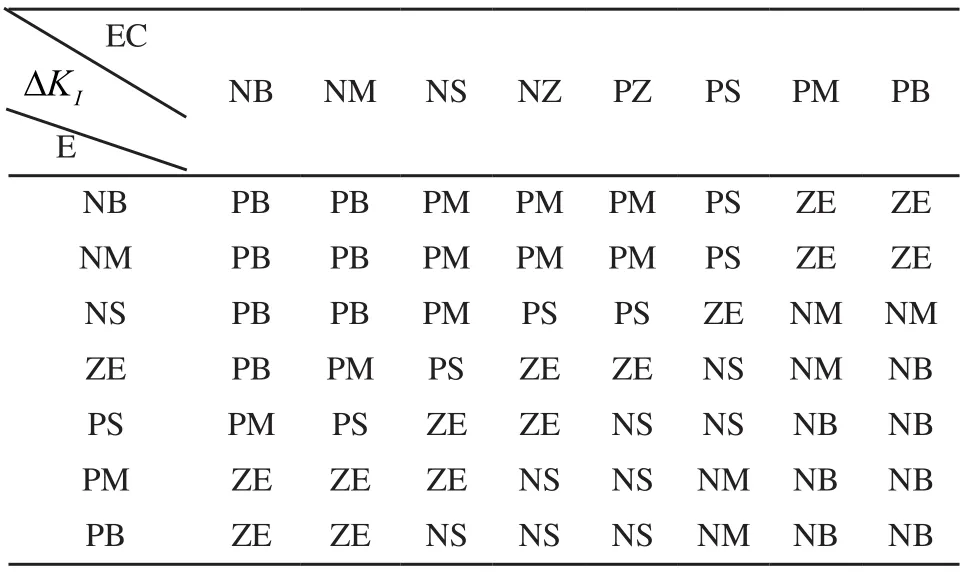
表2 PID参数中IKΔ的模糊推理规则表
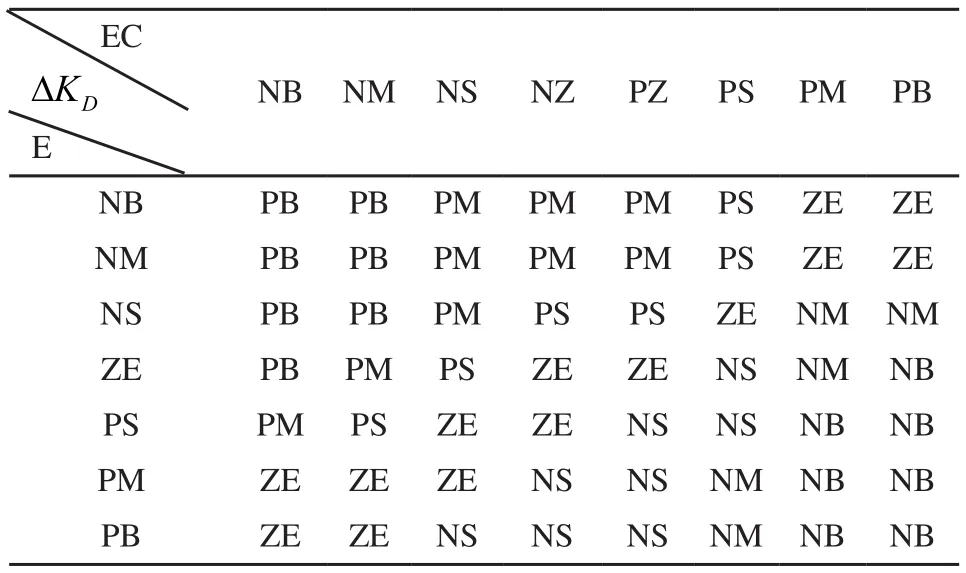
表3 PID参数中DKΔ的模糊推理规则表
表中NB、NM、NS、NZ、ZE、PE、PS、PM和PB分别表示“负大(Negative big)”、“负中(Negative middle)”、“负小(Negative small)”、“负零(Negative zero)”、“零(Zero)”、“正零(Positive zero)”、“正小(Positive small)”、“正中(Positive middle)”和“正大(Positive big)”[9]。智能轮式移动机器人运动系统输出的误差模糊子集为E={NB,NM,NS,ZE,PS,PM,PB},系统输出的误差导数(即误差增量)的模糊子集为DE={NB,NM,NS,NZ,PZ,PS,PM,PB}。
若PID参数KP、KI、KD和系统误差E、系统误差增量DE均服从正态分布,于是可分别建立各自的模糊子集隶属度函数,并利用模糊子集隶属度的赋值表与各个参数的模糊控制模型,进而可以制定PID参数KP、KI、KD的模糊推理表。数字式PID参数KP、KI、KD的增量式迭代过程可表示为:
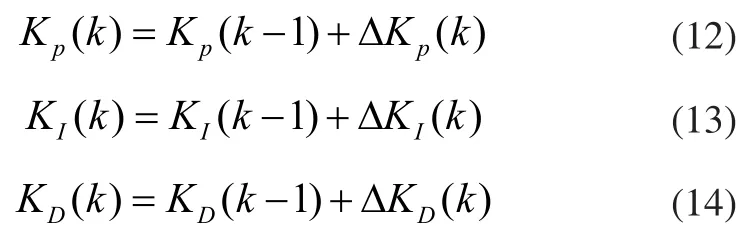
4 仿真结果与分析
本节首先基于轮式机器人运动系统的控制模型分析了运动系统的动态特性,然后对于基于离散模糊自适应PID的轮式机器人运动系统的动态过程进行了仿真分析。
4.1 轮式机器人运动系统控制模型特性分析
在MATLAB(R2011b, MathWorks)平台上对于运动系统的控制模型进行仿真,控制模型的阶跃信号仿真图如图4所示。从图中可以看出,轮式机器人运动系统具有高度的非线性和强时变性。
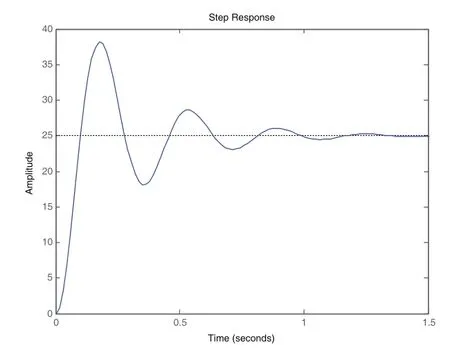
图4 智能轮式机器人运动系统控制模型的系统响应
4.2 基于离散模糊自适应PID的轮式机器人运动系统的仿真分析
为验证所设计离散模糊自适应PID控制器的有效性,本文针对智能轮式机器人的动力学模型在MATLAB(R2011b, MathWorks)平台进行仿真研究。仿真过程中,模糊自适应数字式PID控制器的控制流程如图5所示。
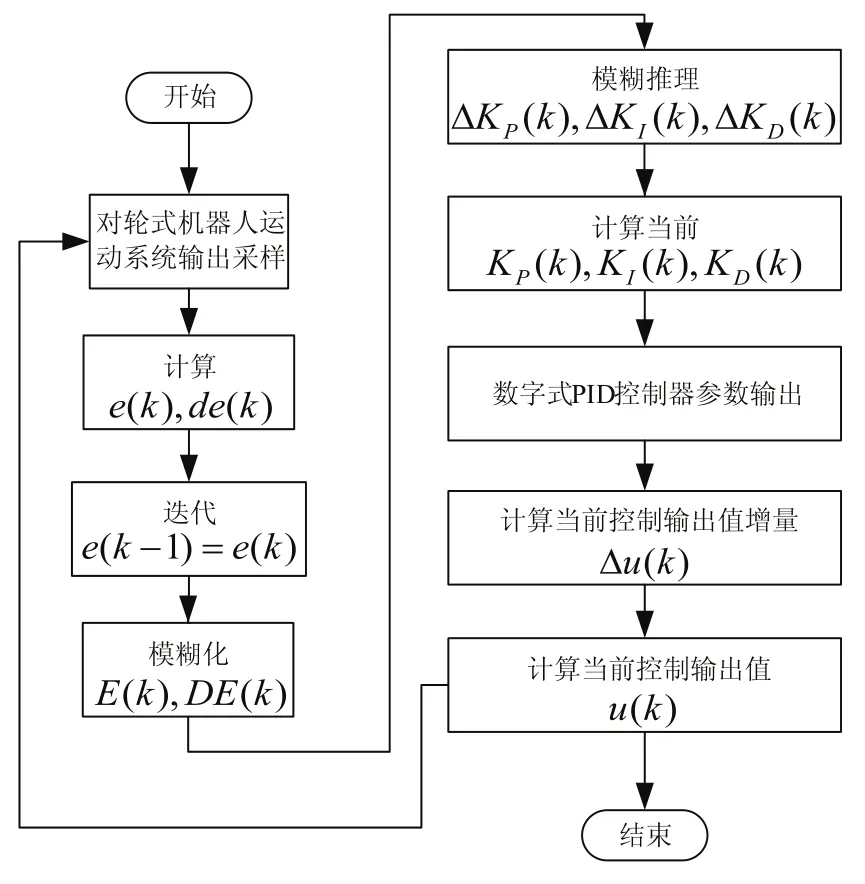
图5 离散模糊自适应PID控制器的控制流程图
基于模糊自适应数字式PID控制器的智能轮式机器人运动系统的仿真如图6所示。仿真过程系统的参考信号采用阶跃信号,由图6可知模糊自适应PID控制器和常规PID控制器的超调量分别为28%和67.5%,调节时间分别为35s和53s,峰值时间分别为95s和120s。此外,模糊自适应PID控制器仅有一个波峰即达到稳定,而常规PID控制器经过多次波峰才趋于稳定,调节时间过长,所以模糊自适应PID的控制性能明显优于常规PID控制器的控制效果。
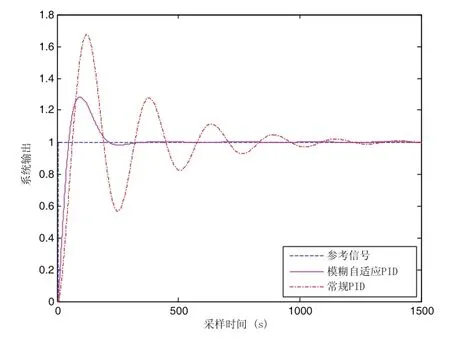
图6 智能轮式机器人运动系统的仿真图
5 结束语
本文基于智能轮式机器人的动力学基本理论,建立了轮式机器人运动系统的动力学模型,并阐述了轮式机器人运动系统的连续与离散两种控制模型。在此基础上,本文通过将模糊推理理论与离散式PID控制算法相结合的方法,综合了二者的优势,提出了离散式模糊自适应PID控制器。最后,本文基于MATLAB平台,将离散式模糊自适应PID控制器与常规离散式PID控制器运用于轮式机器人运动系统的离散控制模型上进行了仿真对比,仿真结果显示,离散式模糊自适应PID控制器的控制性能明显优于常规离散式PID控制器。今后的研究中,在研究单个轮式机器人运动系统控制方法的基础上,将进一步研究多机器人的编队控制问题。
[1] S. János, I. Matijevics, Implementation of Potential Field Method for Mobile Robot Navigation in Greenhouse Environment with WSN Support[A].in 2010 8th International Symposium on Intelligent Systems and Informatics (SISY),[C].2010,319-323.
[2] A. C. Ã, I.Macaluso, The perception loop in CiceRobot, a museum guide robot[J].Neurocomputing,2009,72(4-6):760-766.
[3] F. Liu, S. Liang, X. Xian, H. Bi, Optimal path planning for mobile robot in consideration of road attributes[J].ICIC Express Letters,2012,6(1):281-287.
[4] 王伟,张晶涛,柴天佑.PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355.
[5] 陆磊,模糊PID控制在轮式机器人上的应用[J].微型电脑应用,2010,26(12):31-33.
[6] 丁度坤,邹焱飚,张铁,谢存禧.喷涂机器人关节的PID自适应模型[J].华南理工大学学报(自然科学版),2009,37(4):90-94.
[7] 李冬,周利坤.清洗机器人自适应PID控制研究[J].计算机仿真,2012,29(12):239-242.
[8] 宋新甫,梁波.基于模糊自适应PID的风力发电系统变桨距控制[J].电力系统保护与控制,2009,37(16):50-58.
[9] 陈刚,张为公.基于模糊自适应PID的汽车驾驶机器人的车速控制[J].汽车工程,2012,34(6):511-516.

